2017年中考“抽样与数据分析”专题解题分析

周建英

（浙江省台州市玉环城关第一初级中学）

《义务教育数学课程标准（2011年版）》（以下简称《标准》）中将数据分析观念解释为，了解现实生活中有许多问题应该先做调查研究，收集数据，通过分析做出判断，体会数据中蕴含的信息；了解对于同样的数据可以有多种分析的方法，需要根据问题的背景选择合适的方法；通过数据分析体验随机性.一方面，对于同样的事情每次收集到的数据可能不同；另一方面，只要有足够的数据就可能从中发现规律.这段表述中点明了统计的核心是数据分析.2017年全国各地中考试卷中对“抽样与数据分析”内容的考查也紧紧围绕《标准》的要求展开，不但注重了对基础知识和基本技能的考查，也注重对基本思想和基本活动经验的考查.

一、试题分析

“抽样与数据分析”是统计的核心内容.数据是信息的载体，这个载体包括数，也包括言语、信号、图象，凡是能够承载事物信息的东西都构成数据，而统计学就是通过这些载体来提取信息进行分析的科学和艺术.在2017年全国各地的中考试题中，对于“抽样与数据分析”的考查，从内容上看既有基本概念的判断，又有基本统计量的运算，以及基本思想的运用；从呈现方式上看涵盖了数据、图表、图象等方式.这就要求学生掌握必要的数据处理技能，通过对直观数据或图表信息的分析，熟练地进行数据的收集、整理、描述、分析，做出合理的推断与预测.

1.考查基本概念，关注基础知识

2017全国各地的中考试题中“抽样与数据分析”部分的试题，有些关注的是基本概念与基础知识的考查，这类试题大部分为选择题.试题在这一层考查的知识点有调查方式的选择、抽样调查的特点、平均数、众数、中位数、方差的意义等，解决这类问题的关键是理解概念.

（1）调查方式的选择.

例1（青海·西宁卷）下列调查中，适合采用全面调查（普查）方式的是（）.

（A）了解西宁电视台《教育在线》栏目的收视率

（B）了解青海湖斑头雁种群数量

（C）了解全国快递包裹产生包装垃圾的数量

（D）了解某班同学“跳绳”的成绩

解析：对西宁电视台《教育在线》栏目的收视率、青海湖斑头雁种群数量数量情况、全国快递包裹产生包装垃圾的数量的调查，适合抽样调查，故选项A，B，C错误；对某班同学“跳绳”的成绩情况的调查，适合全面调查，故选项D正确.

【评析】让学生经历简单的数据统计过程，运用合理的方式收集数据是数据分析的基本技能.一般来说，调查范围较广，或具有破坏性的，适合抽样调查.例如，调查灯泡的使用寿命，火柴质量等.调查范围较小，需要的数据更精确的，适合全面调查.例如，某班学生上学所用的交通工具等.全面调查和抽样调查是数据分析中收集数据的方法，能达到对数据分析基本概念的考查，再如湖北省襄阳卷、重庆卷中也对调查方式进行了考查.

（2）抽样调查的特点.

例2（四川·内江卷）为了解某市老人的身体健康状况，需要抽取部分老人进行调查，下列抽取老人的方法最合适的是（）.

（A）随机抽取100位女性老人

（B）随机抽取100位男性老人

（C）随机抽取公园内100位老人

（D）在城市和乡镇各选10个点，每个点任选5位老人

解析：为了解某市老人的身体健康状况，需要抽取部分老人进行调查，在城市和乡镇各选10个点，每个点任选5位老人，这种抽取老人的方法最合适．故此题选择选项D．

【评析】样本的最终作用是用来估计总体的情况，因此要得到较为准确的结果，对样本的代表性要求就比较高.选项A，B，C中的三种调查方式所抽取的样本都不具有代表性，因此不合理，选项D在各个乡镇任选10个点，且每个点任选5个人，这样的抽取具有随机性，选出的样本也具有代表性，因而选项D正确.

对抽样调查方式特点的考查的试题在设计上都是以选择题形式呈现，考查了学生对简单随机抽样的理解，背景贴近学生的生活实际，符合《标准》中对基础知识的考查要求.

（3）平均数、众数、中位数、方差的概念及意义.

例3（贵州·六盘水卷）已知A组四人的成绩分别为90，60，90，60，B组四人的成绩分别为70，80，80，70，用下列哪个统计知识分析区别两组成绩更恰当（）.

（A）平均数（B）中位数

（C）众数（D）方差

解析：平均数可以反映一组数据的平均水平；众数可以反映一组数据的多数水平；中位数可以反映一组数据的中间位置水平；方差是反映数据的波动程度.两组数据的平均数、中位数相同，众数和方差不同，根据各统计量的意义，应考虑的统计量是方差，故此题选择选项D.

【评析】平均数、中位数、众数、方差都是基本的数据分析统计量，在实际问题情境中掌握不同统计量的应用是完成统计决策的基本要求.此题是考查学生对几个统计量意义的理解，而不是单纯的计算，考查目标体现了《标准》对统计基础知识的要求.2017年全国各地中考试卷中，像这种直接考查统计量意义的还有湖南省湘潭卷、长沙卷、郴州卷，浙江省嘉兴卷，辽宁省沈阳卷，黑龙江省齐齐哈尔卷等.

2.考查统计量的求法，强调运算能力

从近几年中考试题来看，数据的分析和处理已成为一个重要考点.平均数、中位数、众数和方差作为简单统计量，对它们的直接计算或理解运用就大量出现在各地的中考试题中.这些试题既考查了学生的运算能力，同时又侧重于对统计量意义的理解与运用，体现《标准》中对学生的数据分析观念的培养的要求.

（1）直接列数据计算.

例4 （上海卷）数据2，5，6，0，6，1，8的中位数和众数分别是（）.

（A）0和6（B）0和8

（C）5和6（D）5和8

解析：将2，5，6，0，6，1，8按照从小到大排列是0，1，2，5，6，6，8，位于中间位置的数为5，故中位数为5.数据6出现了2次，出现次数最多，故这组数据的众数是6，中位数是5.故此题选择选项C．

例5（黑龙江·绥化卷）在一次射击训练中，某位选手五次射击的环数分别为5，8，7，6，9．则这位选手五次射击环数的方差为___．

【评析】准确地进行统计量的运算是数据分析的基础.例4是罗列数据来求中位数和众数，解决此题的关键是理清算法，明确求中位数要先将数据排序.例5是直接计算方差，解决此题的关键是熟记方差的计算公式.2017年全国各地中考试题中对统计量的直接计算的试题也很多，如山东省日照卷、广东卷、浙江省杭州卷、广西贵港卷、河南卷、山东省威海卷等都出现了对平均数、中位数、众数和方差的直接计算.

（2）借助图表计算.

例6 （贵州·安顺卷）如图1是根据某班40名同学一周的体育锻炼情况绘制的条形统计图．那么该班40名同学一周体育锻炼时间的众数、中位数分别是（）.

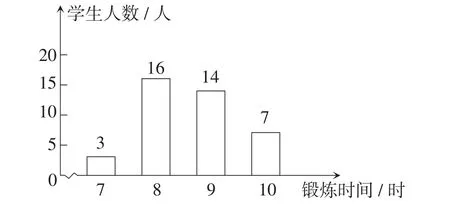
图1

（A）16，10.5（B）8，9

（C）16，8.5（D）8，8.5

解析：众数是一组数据中出现次数最多的数，即8；由中位数的定义可知，将这组数据从小到大的顺序排列后，应取第20和第21个数据的平均数为中位数，而这两个数据都是9，所以这组数据的中位数是9.故此题选择选项B.

例7（湖南·常德卷）如图2是根据我市某天七个整点时的气温绘制成的统计图，则这七个整点时气温的中位数和平均数分别是（）.

图2

（A）30，28（B）26，26

（C）31，30（D）26，22

解析：由图2可知，把7个数据从小到大排列为22，22，23，26，28，30，31，中位数是第4位数，第4位是26，所以中位数是26．平均数是（22×2+23+26+28+30+31）÷7=26，所以平均数是26．故此题选择选项B.

例8（海南卷）今年3月12日，某学校开展植树活动，某植树小组20名学生的年龄情况如表1所示.

表1

则这20名同学年龄的众数和中位数分别是（）.

（A）15，14（B）15，15

（C）16，14（D）16，15

解析：因为12岁的有1个人，13岁的有4个人，14岁的有3个人，15岁的有5个人，16岁的有7个人，

所以出现次数最多的数据是16.

所以20名学生年龄的众数为16岁.

因为一共有20名学生，

所以其中位数应该是第10名和第11名学生的年龄的平均数.

求得中位数为（15+15）÷2=15.

所以20名学生年龄的中位数为15.

故此题选择选项D.

【评析】以上三道试题都是借助图表求统计量.例6是条形图，例7是折线图，例8是统计表.统计图和统计表是描述数据的重要手段，解决这类问题的关键是读懂统计图和统计表所包含的数据信息，并且能将原始数据根据需要进行整理.同样，在2017年全国各地的中考试题中考法类似的还有江苏省苏州卷、四川省宜宾卷、青岛卷、浙江省丽水卷、湖北省十堰卷、湖北省黄冈卷、四川卷等，其中以表格形式出现最多.

（3）已知一个统计量，求其他量.

例9（江西卷）已知一组从小到大排列的数据2，5，x，y，2x，11的平均数与中位数都是7，则这组数据的众数是____．

解析：因为一组从小到大排列的数据2，5，x，y，2x，11的平均数与中位数都是7，

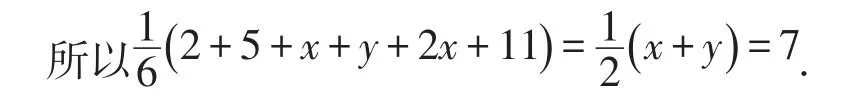
解得y=9，x=5.

所以这组数据的众数是5．

故此题答案为5．

【评析】此题是已知平均数和中位数求众数，解决此题需要结合平均数和中位数的定义，得到两个条件，联立方程组求得x和y的值.此题考查了学生对几个数据分析量的意义及求法的理解和掌握程度，以及综合运算的能力.与此题考法类似的还有浙江省宁波卷和内蒙古通辽卷.

3.突出统计思想，强化应用意识

抽样与数据分析里体现的数学思想主要有随机思想、样本估计总体、统计推断等.突出统计的基本思想可以使学生形成统计特有的观念，让学生体会用数据说话，以样本估计总体，预测结果的意义.学生在感悟这些思想方法后，不仅可以提高思维品质，而且还为他们今后进一步学习概率统计知识做铺垫.

（1）考查用样本估计总体的思想.

用样本估计总体是统计学的重要思想，也是统计价值的应用体现.面对一组数据能引发思考，能够推测可能的结果，以及自觉运用统计的方法解决有关的问题是统计的学习目标.2017年全国各地很多中考试题都侧重于考查利用样本估计总体的思想.

例10（浙江·台州卷）家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康.某市药监部门为了解市民家庭处理过期药品的方式，决定对全市家庭做一次简单随机抽样调査．

（1）下列选取样本的方法最合理的一种是____（只需填上正确答案的序号）．

①在市中心某个居民区以家庭为单位随机抽取；

②在全市医务工作者中以家庭为单位随机抽取；

③在全市常住人口中以家庭为单位随机抽取．

（2）本次抽样调査发现，接受调査的家庭都有过期药品，现将有关数据呈现如图3和图4所示.

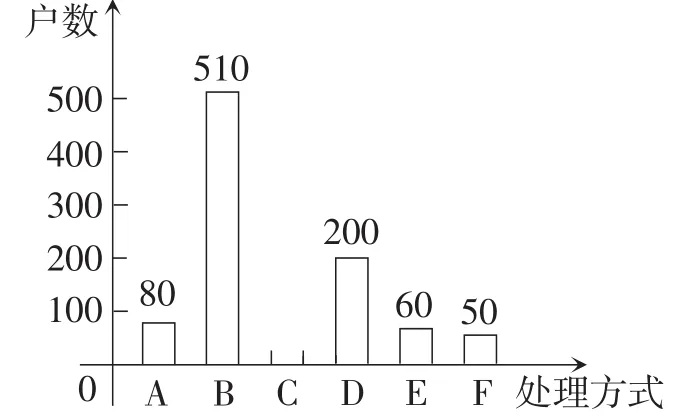
图3

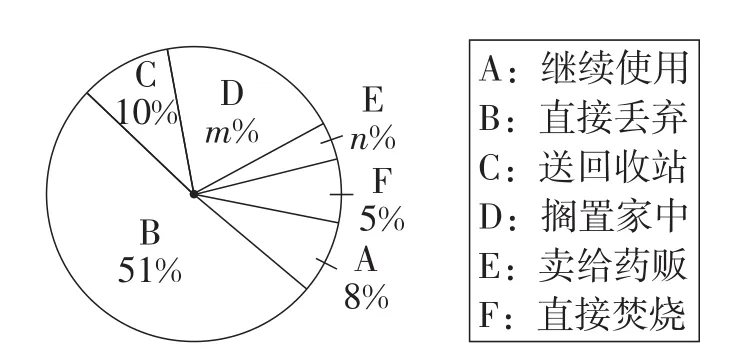
图4

①m=____，n=____；

②补全条形统计图；

③根据调査数据，你认为该市市民家庭处理过期药品最常见的方式是什么？

④家庭过期药品的正确处理方式是送回收点，若该市有180万户家庭，试估计大约有多少户家庭处理过期药品的方式是送回收点．

解析：（1）简单随机抽样，即按随机性原则，从总体单位中抽取部分单位作为样本进行调查，以其结果推断总体有关指标的一种抽样方法.随机原则是在抽取被调查单位时，每个单位都有同等被抽到的机会，被抽取的单位完全是偶然性的.由此可以得出答案为③.

（2）①抽样调査的家庭总户数为80÷8%=1000.

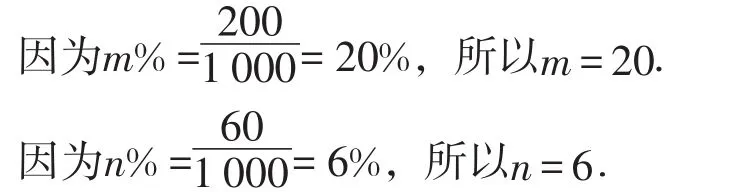
故此题答案为20，6.

②C类户数为1000-（80+510+200+60+50）=100，补充的条形统计图如图5所示.

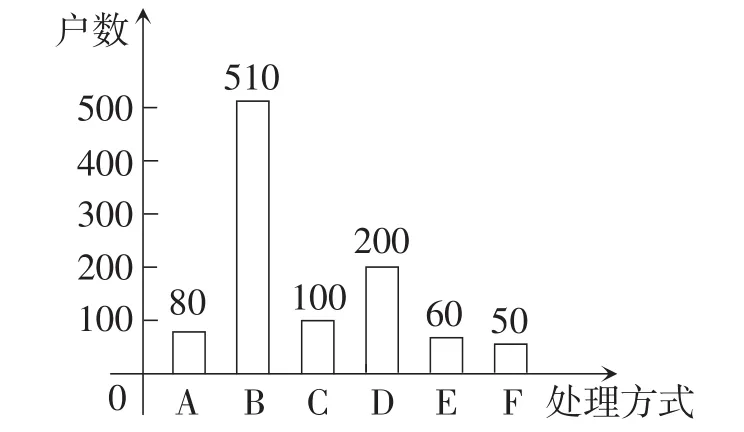
图5

③根据调査数据，即可知道该市市民家庭处理过期药品最常见的方式是B类.

④180×10%=18（万户）.

若该市有180万户家庭，估计大约有18万户家庭处理过期药品的方式是送回收点.

例11（山东·临沂卷）为了解某校学生对《最强大脑》《朗读者》《中国诗词大会》《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如表2、图6所示的统计图表.

表2：学生最喜爱的节目人数统计表

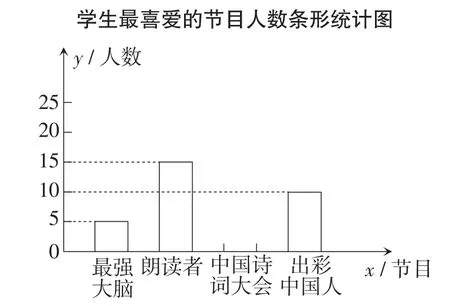
图6

根据以上提供的信息，解答下列问题.

（1）x=_____，a=_____，b=_____；

（2）补全如图6所示的条形统计图；

（3）若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少？

解析：（1）根据《最强大脑》的人数除以所占的百分比确定出x的值为50，进而求出a与b的值，即20和30.

（2）根据a的值，补全条形统计图即可（如图7）.

图7

（3）因为1000×40%=400.

所以该校约有400名学生最喜爱《中国诗词大会》.

【评析】例10中出现两个统计图，第（1）小题考查了抽样调查的注意点，第（2）小题分四个小问，前三问是根据图中数据进行相应计算，并补全图形，第四问根据样本结果推测全市180万户家庭有多少户家庭处理过期药品的方式是送回站点，考查了用样本估计总体的思想.例11出现一个条形统计图和一个统计表，也是先进行数据计算，再用样本估计总体进行推断.两道题中都着重考查了用样本估计总体的思想.2017年各地的中考试题中考查这一思想的不在少数，如山东省德州卷和青岛卷，浙江省绍兴卷、宁波卷、金华卷和嘉兴卷，四川省泸州卷、南充卷、广安卷、达州卷，广西贵港卷，江苏省盐城卷、连云港卷和徐州卷，湖南省湘潭卷、张家界卷、岳阳卷，湖北省宜昌卷等.

（2）运用数据进行合理性解释和推断.

学统计不仅要学会从图中获取信息，用公式进行计算，更重要的是要有统计意识，学会用统计的思想方法考虑问题，用统计知识推断或帮助我们做出决策.在做具体推断时要依据问题要求和实际情况进行多角度思考，力戒判断的片面性.2017年全国各地中考试题中这类题目也出现较多.

例12（内蒙古·通辽卷）某校举办了一次成语知识竞赛，满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀，这次竞赛中，甲、乙两组学生成绩分布的折线统计图如图8所示，成绩统计分析表如表3所示.

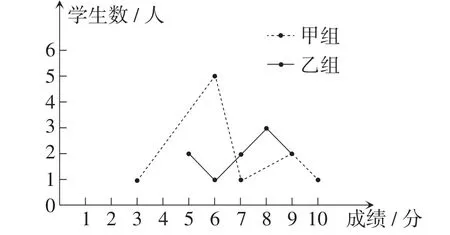
图8

（1）求出如表3所示的成绩统计分析表中a，b的值.

表3

（2）小英同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察表3判断，小英是甲、乙哪个组的学生.

（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组.试写出两条支持乙组同学观点的理由.

解析：（1）由图8可知，因为甲组成绩从小到大排列为3，6，6，6，6，6，7，9，9，10，所以其中位数a=6，

乙组学生成绩的平均分为

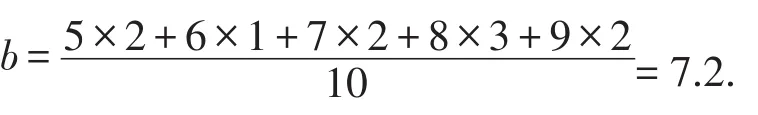
（2）因为甲组的中位数为6，乙组的中位数为7.5，而小英的成绩位于全班中上游，

所以小英属于甲组的学生.

（3）①乙组的平均分高于甲组，即乙组的总体平均水平高；

②乙组的方差比甲组小，即乙组的成绩比甲组的成绩稳定.

【评析】此题第（1）小题要求统计表中a，b的值，解决这一问的关键是读懂题意.从统计图中整理出甲、乙两组学生的成绩和对应人数，再根据中位数与平均分的计算方法算出a，b的值.第（2）小题主要考查统计量的意义，根据题意明确需参考的统计量是中位数，只要进行两组中位数计算就能判断小英属于哪一组.第（3）小题的考点也是统计量的意义，但从问题设计上要比第（2）小题含蓄，它没有说明从哪个角度入手，需要学生自己去选择，要综合比较两组的平均数、中位数、方差做出说明，对学生的数据分析观念和应用意识提出了更高的要求.

4.与概率、代数综合，凸显方法的应用

对数据分析知识的考查，多数是以单一形式出现，一般不涉及其他知识.但是近年来也出现了将数据分析知识与其他知识联系起来进行综合考查的题目，如将数据分析与概率和代数知识综合.2017年全国各地中考试题中这类题目的形式活泼，对考查学生的能力很有意义.

（1）与概率综合.

例13（重庆A卷）重庆某中学组织七、八、九年级学生参加“直辖20年，点赞新重庆”作文比赛，该校将收到的参赛作文进行分年级统计，绘制了如图9所示的两幅不完整的统计图，根据图中提供的信息完成以下问题.

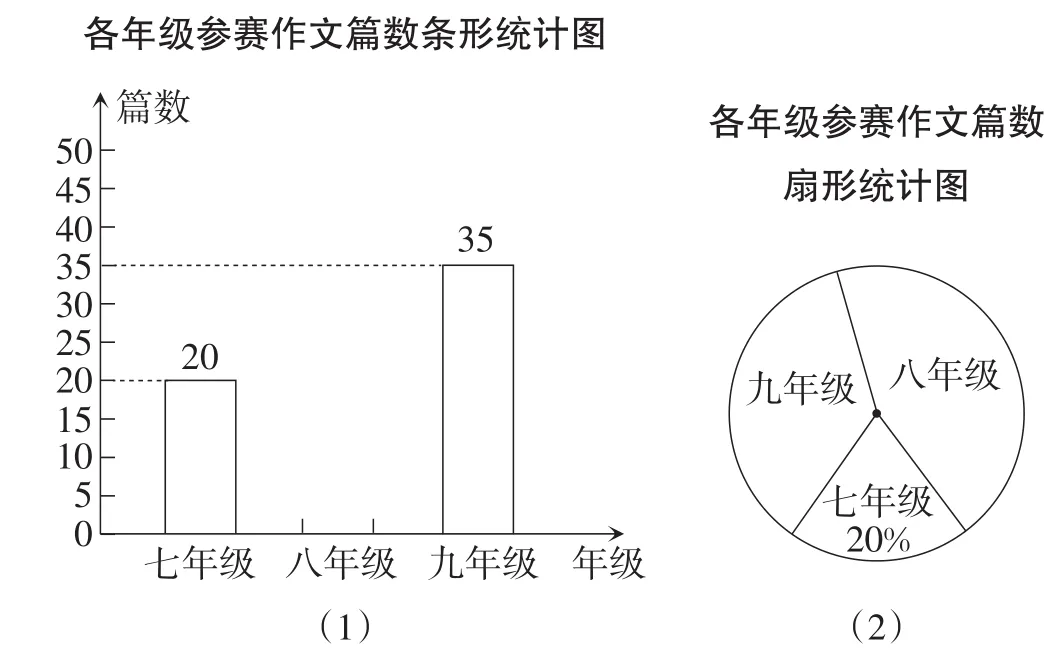
图9

（1）扇形统计图中九年级参赛作文篇数对应的圆心角的度数是_____，并补全条形统计图；

（2）经过评审，全校有4篇作文荣获特等奖，其中有一篇来自七年级，学校准备从特等奖作文中任选两篇刊登在校刊上，试利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.

解析：（1）由图9可知，20÷20%=100.

100-20-35=45，补全的条形统计图如图10所示.

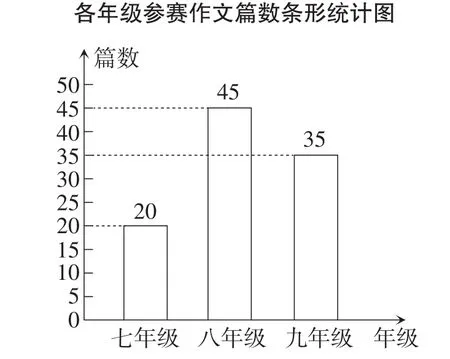
图10

（2）假设4篇荣获特等奖的作文分别为A，B，C，D，其中A代表七年级获奖的特等奖作文．

画树状图法（如图11）：共有12种等可能的结果，七年级特等奖作文被选登在校刊上的结果有6种，

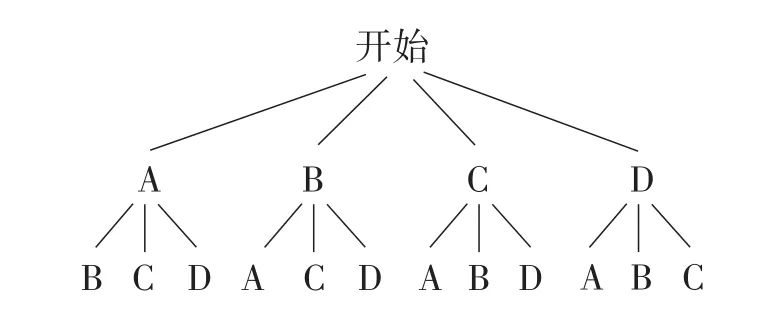
图11

【评析】在2017年全国各地中考试题中，出现了大量统计与概率综合性考查的试题.例如，重庆卷，江苏省苏州卷、无锡卷，贵州省黔东南卷，山东省枣庄卷、烟台卷，湖北省襄阳卷、十堰卷、荆州卷、孝感卷、咸宁卷，湖南省长沙卷，四川省自贡卷，新疆生产建设兵团卷，青海省西宁卷，广西河池卷等.这些试题均考查了利用题中的数据信息进行统计方法的正确选择，通过计算进行决策和判断，并综合利用概率知识解决问题，问题涉及到数据分析和概率两个知识点，但共用一组时，问题设计自然，过渡巧妙.

（2）与代数、方程、不等式综合.

例14（浙江·衢州卷）根据衢州市统计局发布的统计数据显示，衢州市近5年国民生产总值数据如图12所示，2016年国民生产总值中第一产业、第二产业、第三产业所占比例如图13所示.

图12

图13

根据图中信息，解答下列问题.

（1）求2016年第一产业生产总值（精确到1亿元）；

（2）2016年比2015年的国民生产总值增加了百分之几（精确到1%）？

（3）若要使2018年的国民生产总值达到1573亿元，求2016年至2018年我市国民生产总值的平均年增长率（精确到1%）.

解析：（1）1300×7.1%≈92（亿元）．

答：2016年第一产业生产总值大约是92亿元.

（2）（1300-1204）÷1204×100%=96÷1204×100%≈8%．

答：2016年比2015年的国民生产总值大约增加了8%；

（3）设2016年至2018年我市国民生产总值的年平均增长率为x，

根据题意，得1300(1+x)2=1573.

解得(1+x)2=1.21.

解得x=0.1或x=-2.1（负值不符合题意，舍去）．

所以2016年至2018年我市国民生产总值的年平均增长率约为10%.

【评析】此题中三道小题均需要从题中获取数据进行计算，其中第（3）小题需结合一元二次方程知识进行解决.抽样与数据分析和代数知识的综合，体现了这一板块知识在中考考查的综合性，也凸显出不同板块知识的自然融合.

二、解法分析

在《标准》中，数据分析观念包含着如下三层意思.第一，经历数据分析的过程，体会数据中蕴含着信息；第二，掌握数据分析的基本方法，根据问题的背景选择合适的方法；第三，通过数据分析，感受数据的随机性.根据《标准》，各地的中考试题考查的重点是会收集、整理、描述、分析数据，感受数据分析的基本过程，会将数据用于决策，体会其中蕴含的随机意识和统计基本思想.因此，在解题方面应做好以下三点：（1）理解概念，准确运算，合理选择；（2）具备读图、释图、作图能力，灵活进行数据整理；（3）培养数据分析观念，强化应用意识.

1.理解概念，准确运算，合理选择

2017年全国各地的中考试题中有单个概念作为考点的，但也有一些试题中涉及到了多个概念的判断.相对来说，这些试题综合性较高，解决此类题目的关键是准确理解各个概念，分清不同的概念所代表的意义，能在具体的问题情境中准确运算，并合理选择统计量决策.

例15 （四川·眉山卷）下列说法错误的是（）.

（A）给定一组数据，那么这组数据的平均数一定只有一个

（B）给定一组数据，那么这组数据的中位数一定只有一个

（C）给定一组数据，那么这组数据的众数一定只有一个

（D）如果一组数据存在众数，那么该众数一定是这组数据中的某一个

解析：给定一组数据，那么这组数据的平均数、中位数一定只有一个，故选项A，B正确；给定一组数据，那么这组数据的众数不一定只有一个，故选项C错误；如果一组数据存在众数，那么该众数一定是这组数据中的某一个，故选项D正确.故此题选择选项C.

【评析】此题考查了对平均数、中位数、众数的意义的理解，而不是单纯地对统计量进行计算.从三个统计量的求法中可以发现平均数、中位数应是唯一确定的，众数是不确定的.解决这道题不但要知道如何计算统计量，而且要从统计量的定义与算法中概括出结果是否确定，因此也是要建立在对概念深刻理解的基础上的.

例16（江苏·徐州卷）在《朗读者》节目的影响下，某中学开展了“好书伴我成长”读书话动，为了解5月份八年级300名学生读书情况，随机调查了八年级50名学生读书的册数，统计数据如表4所示.

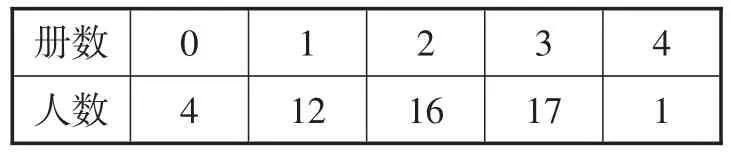
表4

关于这组数据，下列说法正确的是（）.

（A）中位数是2（B）众数是17

（C）平均数是2（D）方差是2

解析：观察表格，可计算出平均数为

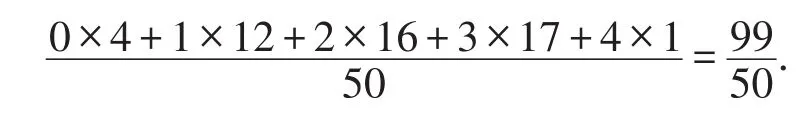
因为这组样本数据中3出现17次，出现次数最多，

所以这组数据的众数为3.

因为将这组数据从小到大排列后处于中间的两个数为2，

所以这组数据的中位数为2.

故此题选择选项A.

【评析】此题考查的是各统计量的计算，数据以表格形式出现，这就要求学生先理解表格中数据的意义，不然就会造成判断错误.例如，选择选项B的学生就是没有理解好册数与人数到底哪个是我们所统计的数据，而造成错误的判定，中位数、平均数、方差都需要进行计算，但此题先判断中位数会简单点，总共50名学生，应该将数据从小到大排列后取第25个和第26个数据的平均数，而此题中第25个和第26个数据都是2，因此中位数为2，故选项A正确.

数据分析的首要任务是先要准确地进行各统计量的计算.在2017年全国各地的中考试题中出现了大量对平均数、中位数、众数和方差计算的试题，数据呈现方式有直接排列或用统计图表给出的，在不同的背景下呈现，关键是要准确理解题意，正确进行运算.

2.强化读图、释图、作图能力，灵活进行数据整理

数据分析不仅要求学生会用统计图表表示数据，还要求学生理解各种统计图表表示的意义和作用.2017年全国各地的中考试题多以现实的统计图表为载体，注重考查学生读图、释图的能力.

例17（贵州·遵义卷）贵州省是我国首个大数据综合实验区，大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是部分四类生活信息关注度统计图表，试根据图14、图15中提供的信息解答下列问题.

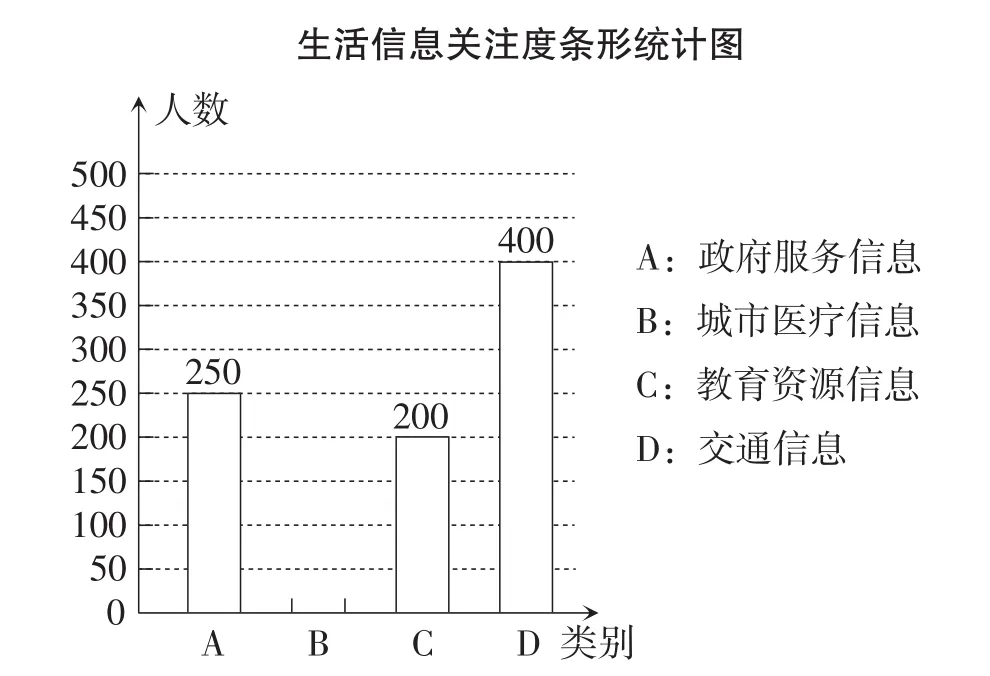
图14

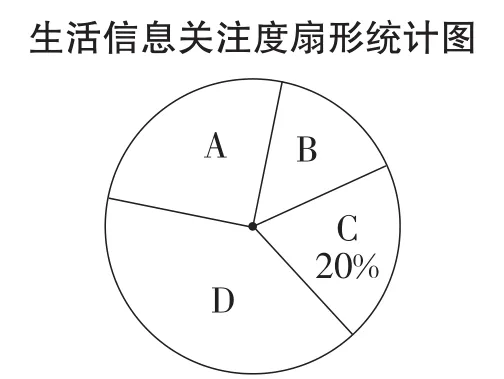
图15

（1）本次参与调查的人数为___；

（2）关注城市医疗信息的人数为___，并补全条形统计图；

（3）扇形统计图中，D部分的圆心角的度数是___；

（4）说一条你从统计图中获取的信息.

解析：（1）由C类别人数占总人数的20%，得本次参与调查的人数为200÷20%=1000.

所以本次参与调查的人数为1000人.

（2）根据各类别人数之和等于总人数，可得B类别的人数.所以关注城市医疗信息的有150人.补全条形统计图如图16所示.

图16

（4）由条形统计图，可知市民关注交通信息的人数最多.

例18（河南卷）为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如表5和图17所示的两个尚不完整的统计图表.

表5：调查结果统计表

图17

试根据以上图表，解答下列问题.

（1）填空：这次被调查的同学人数共有____，a+b=____，m=____；

（2）求扇形统计图中扇形C的圆心角度数；

（3）该校共有1000人，试估计每月零花钱的数额x在60≤x＜120范围的人数.

解析：（1）用B组的人数除以B组人数所占的百分比，即可得这次被调查的同学的人数.利用A组的人数除以这次被调查的同学的人数，即可求得m的值.用总人数减去A，B，E组的人数，即可求得a+b的值.答案分别为50，28，8.

（2）先求得C组人数所占的百分比，乘以360°，得扇形统计图中扇形C的圆心角度数，即（1-8%-32%-16%-4%）×360=40%×360=144°.所以扇形统计图中扇形C的圆心角度数为144°.

（3）用总人数1000乘以每月零花钱的数额x在60≤x＜120范围的人数的百分比即可求得，即1000×.所以每月零花钱的数额x在60≤x＜120范围的人数为560人.

【评析】统计图和统计表是描述数据的重要手段，可以直观地表示数据，它是获取数据的一种重要形式.以上两道试题均考查了学生读图、释图、作图的能力，因此，要具备准确地从图表数据中获取信息和处理信息的能力.培养学生对不同的统计图表的内在联系和本质特征的理解能力，这也是《标准》的要求.

3.培养数据分析观念，强化应用意识

学习统计最有效的方法是真正投入到产生和发展统计的全过程.在丰富的实例中体会抽样的必要性和随机抽样的重要性，并根据样本的平均数、方差等统计量估计总体的特征，体会用样本估计总体的思想，从而学会用数据解决生活中与统计有关的问题的意识，建立数据分析观念，强化应用意识.

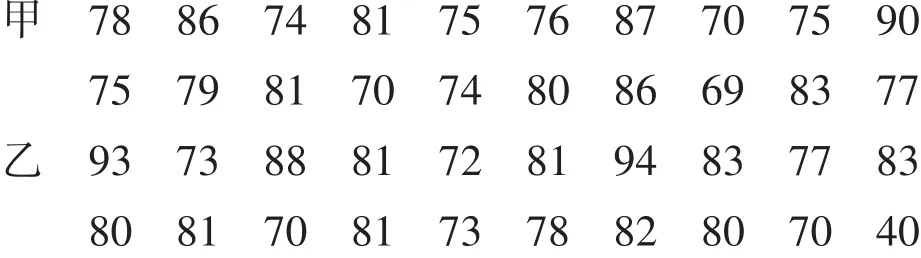
例19（北京卷）某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，试补充完整.

收集数据：从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下.

整理、描述数据：按如表6所示的分数段整理、描述这两组样本数据.

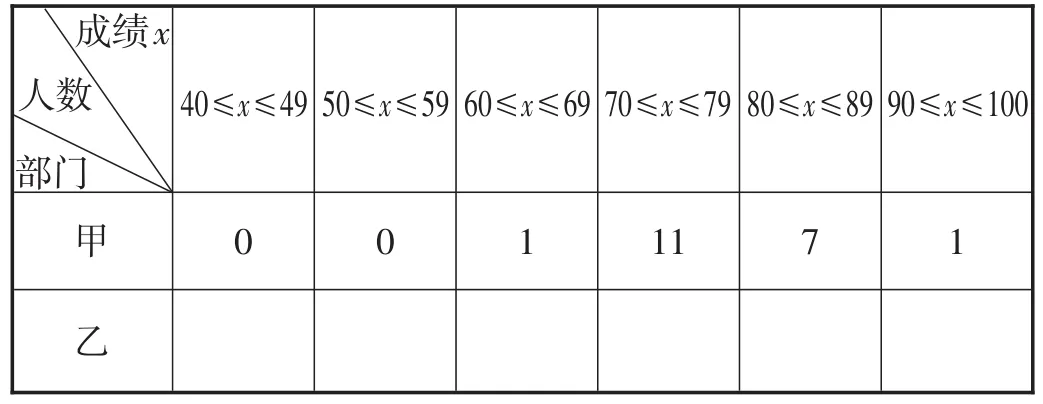
表6

说明：成绩80分及以上为生产技能优秀，70～79分为生产技能良好，60～69分为生产技能合格，60分以下为生产技能不合格.

分析数据两组样本数据的平均数、中位数、众数如表7所示.

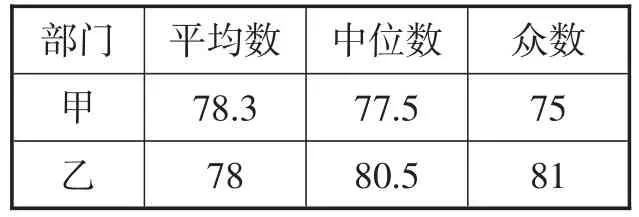
表7

得出结论：

（1）估计乙部门生产技能优秀的员工人数为____；

（2）可以推断出____部门员工的生产技能水平较高，理由为______（至少从两个不同的角度说明推断的合理性）.

解析：（1）按题中表格进行各分数段人数整理，可知乙部门样本的优秀率为，则整个乙部门的优秀率也是60%，因此估计乙部门生产技能优秀的员工人数为400×60%=240（人）；

（2）答案不唯一，言之有理即可.

可以推断出甲部门员工的生产技能水平较高，理由如下.

①甲部门生产技能测试中，测试成绩的平均数较高，表示甲部门生产技能水平较高；

②甲部门生产技能测试中，没有生产技能不合格的员工．

可以推断出乙部门员工的生产技能水平较高，理由如下.

①乙部门生产技能测试中，测试成绩的中位数较高，表示乙部门生产技能水平优秀的员工较多；

②乙部门生产技能测试中，测试成绩的众数较高，表示乙部门生产技能水平较高．

【评析】此题注重呈现统计过程的完整性，结合具体情境在第（1）小题中先进行简单的样本估计总体的计算，第（2）小题中要对哪个部门员工的生产技能水平较高进行推断，并要求从两个角度进行合理性说明.至于从什么角度说明，题中并没有提供思路，这就要求学生根据统计知识合理地选择恰当的统计量进行说明，重视对用统计知识进行推断与决策的考查.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］吴增生.用数学发展智慧：基于脑、适于脑、发展脑的数学教学策略［M］.南昌：江西教育出版社，2016.

［4］王华.2016年中考“事件的概率”专题解题评析［J］.中国数学教育（初中版），2017（3）：46-53，64.

［5］王宇刚，张英.2015年中考数学试题“抽样与数据分析”专题解题评析［J］.中国数学教育（初中版），2016（3）：18-26.