“平行线分线段成比例定理”证法探析

张艳娇，李海东

（人民教育出版社中学数学室）

一、问题提出

笔者近日收到一封读者来信，提出平行线分线段成比例定理是研究相似图形的一个基本理论，建议教材给出证明过程，并提供了如下证明方法（以下统称“面积法”）.

已知：如图1，l1∥l2∥l3，他们分别与直线a，b相交于点A，B，C和点D，E，F.求证：

图1

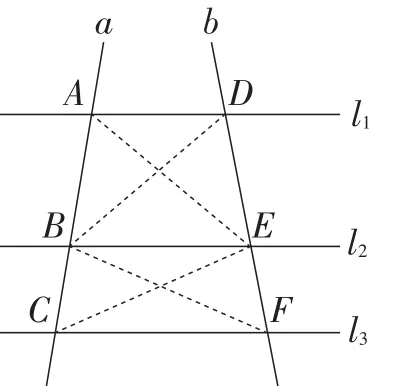
图2

证明：如图2，连接AE，BD，CE，BF.

因为l1∥l2∥l3，

所以S△ABE=S△DEB，S△BCE=S△EFB.

笔者针对这一定理的证明进行了研究，发现多篇文献也提到了这一面积证法.《义务教育数学课程标准（2011年版）》（以下简称《标准》）对这一定理的要求是掌握基本事实，即两条直线被一组平行线所截，所得的对应线段成比例.上述面积法看似简洁清楚，为什么《标准》要求以基本事实的形式呈现，而不要求给出证明呢？之前版本的教材是如何呈现这一定理内容的呢？

二、教材梳理

翻阅历年来人教版的教材，多个版本的教材力图呈现这一定理发生、发展的过程（如1960年版，1963年版，1978年版，1981年版等）.其中1960年版和1963年版先利用平行线等分线段定理证明“平行于三角形一边的直线截其他两边，截得的线段对应成比例”，再进一步证明平行线分线段成比例定理.1978年版和1981年版则在平行线等分线段定理的基础上，直接研究平行线分线段成比例定理，再以推论的形式给出定理在三角形中的应用.下面以1978年版为例介绍教材对这一定理的呈现方式.

（1）教材在《全日制十年制学校初中课本（试用本）数学》第三册首先给出了平行线等分线段定理，并加以证明.

定理：如果一组平行线在一条直线上截得的线段相等，那么在任何一条与平行线相交的直线上截得的线段也相等.

证明过程略.

（2）在《全日制十年制学校初中课本（试用本）数学》第四册以如下形式介绍平行线分线段成比例定理.

如图3，设平行线l1，l2，l3分别截直线a和b于点A，B，C和点D，E，F，我们来研究AB∶BC和DE∶EF之间的关系.

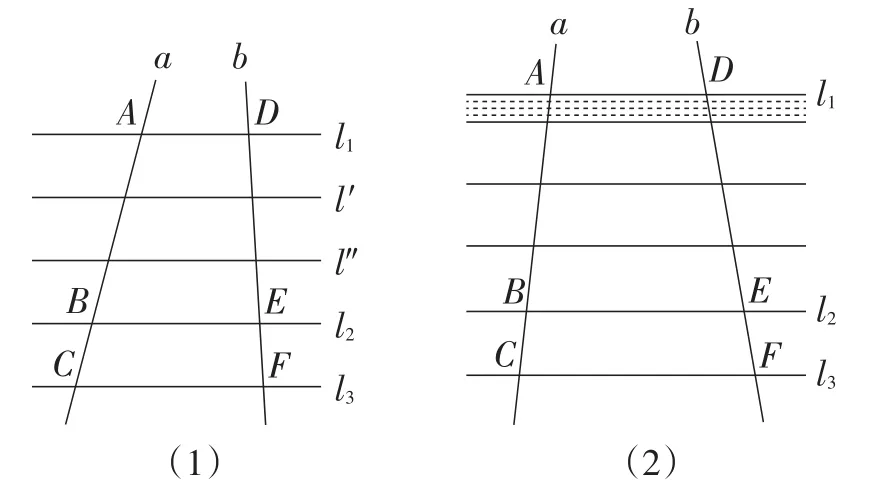
图3

我们知道，线段AB和BC的比是以某一长度单位度量它们所得的量数的比，而且，不论采用哪个长度单位，它们的比都相等.因此，我们取BC为长度单位来度量线段AB.

②如果量3次还有余，量4次不足，而用BC的某一个分数，例如，作单位量剩余线段，恰好4次量尽（如图3（2））. 那么以为长度单位时，BC和AB的量数分别是10和34.因此运用像①中那样作l1的一些平行线的方法，可以知道，因此，也可以得到

这样，我们就得到平行线分线段成比例定理三条平行线截两条直线，所得的四条线段对应成比例.

在1990年版及以后的教材中，对定理的证明进行了弱化.如1990年版及2001年版教材以为特例引出结论，2004年版及现行教材则设置了如下的探究栏目，引导学生通过度量发现规律.

探究：如图4，任意画两条直线l1，l2，再画三条与l1，l2都相交的平行线l3，l4，l5.分别度量l3，l4，l5在l1上截得的两条线段AB，BC和在l2上截得的两条线段DE，EF的长度，相等吗？任意平移l5,还相等吗？

通过对教材的上述梳理，可以发现各版本教材都没有用面积法来证明平行线分线段成比例定理.面积法看似简洁清楚，为什么教材中没有采用呢？

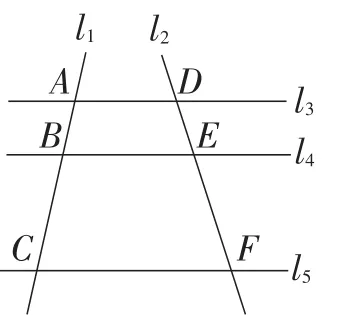
图4

三、面积法解析

上述面积法用到了“同底等高的三角形面积相等”这一结论，其依据是三角形的面积公式.我们回顾一下小学阶段对面积的学习，以人教版教材为例，教材在介绍三角形面积公式时，将三角形的面积转化为平行四边形面积的一半来处理，而平行四边形的面积，是通过割补的方法转化为长方形的面积推导出来的.因此，长方形的面积公式是三角形面积公式的理论基础.

教材在介绍长方形和正方形的面积计算公式时，采用了如下步骤.

第一步，呈现了两名学生用画格子或用面积单位测量长方形面积的活动；第二步，安排了用面积单位摆拼多个长方形的活动，并用表格记录长、宽和面积，以此发现面积单位的个数与长、宽之间的关系；第三步，画出了两个长方形，要求学生量出长和宽，再计算面积.学生测量时会发现第二个长方形的长与宽相等，从而得出正方形面积公式.

在上述对长方形面积公式的推导中，“边长为1cm的正方形面积是1cm2”是作为基本事实给出的.这就涉及了一个问题：以厘米为单位度量，边长是整数的长方形可以由上述摆拼的方法直接得出面积.如果长方形的边长是分数，假设一边长为cm（m，n是正整数），另一边长为1cm，则将n个长方形沿长为cm的一边摆成一列，可拼成一边长分别为mcm和1cm的长方形，面积为mcm2，所以原长方形的面积为新长方形面积的,即原长方形面积为cm2.同理，可得边长为有理数的长方形都可以通过摆拼的方法转化成边长为整数的情况，因此可以得出其面积.如果长方形的边长是无理数呢？由于无理数不能表示成分数的形式，所以边长为无理数的长方形面积公式不能用度量或用摆拼的方法得出.因此，边长为无理数的三角形的面积计算公式也无法据此得出.要想获得长方形面积公式的严格证明，需要用到有理数列逼近无理数的知识，小学阶段显然是无法给出证明的.

联系我们前面提出的问题，用面积法证明平行线分线段成比例定理，是建立在边长为无理数的三角形面积公式依然成立的前提下的，其证明实际也需要用到高等数学中无理数理论及极限的知识.与之前教材中的证明思路相比，两者的理论基础一致，都需要用到高等数学的知识.考虑到初中学生的理论基础及认知水平，教材在此处无法给出定理的严格证明，《标准》也是将这一定理作为基本事实给出.教师在授课时不必强调这一定理的证明过程，应引导学生认识这一定理的推论在判定三角形相似时的作用.

［1］赵维晶，陈吉凯.“平行线分线段成比例”定理的另一证明方法［J］.黑龙江教育（中学版），2004（7/8）：48.

［2］沈颂豪.“平行线分线段成比例定理”的初等证法［J］. 苏州教育学院学报,1998（3）：46.

［3］姚晓风.平行线分线段成比例定理的面积证法［J］. 安徽教育学院学报，2000（6）：63.