序列凸优化的小天体附着轨迹优化
2018-03-16刘延杰朱圣英崔平远
刘延杰,朱圣英,崔平远
(1. 北京理工大学宇航学院,北京 100081;2.深空自主导航与控制工信部重点实验室,北京 100081;3.飞行器动力学与控制教育部重点实验室,北京 100081)
0 引 言
小天体蕴含着丰富的科学信息,相关研究的开展有助于人类认识生命的起源与进化,抵御外来天体的撞击威胁[1]。近年来,随着人类科学技术的发展和经济实力的提升,小天体探测方式逐渐向附着探测和采样返回探测发展。附着探测的开展是人类从目标小天体获得科学信息的有效途径,也是未来人类进行小天体资源利用的前提条件。
目前,人类已经实施了多次小天体附着任务,包括美国宇航局(NASA)的近地小行星交会任务(Near Earth asteroid rendezvous,NEAR),日本宇航局(JAXA)的隼鸟号(Hayabusa)任务和欧空局(ESA)的罗塞塔(Rosetta)任务。此外,日本的“隼鸟2号”(Hayabusa 2)任务在2014年12月发射,预计对C类小行星1999 JU3进行为期一年半的探测,并完成采样返回。美国的OSIRIS-REx探测器在2016年9月发射,对C类小行星101955 Bennu进行采样返回探测,预计2023年返回地球[2]。
小天体附着轨迹的设计对探测器能否安全、准确到达预设的具有科学探测价值的目标区域起着决定性的作用,所设计的轨迹需要能够安全、准确地到达指定着陆点,满足初末状态约束、路径约束、控制约束等多重约束条件,同时使某项重要的性能指标最优化,如燃耗、时间等。
小天体质量体积比较小,形状不规则,这导致其附近呈现不规则弱引力场。引力场建模是研究和分析小天体附近运动行为的基础。经典的球谐系数模型在邻近小天体的空间范围内存在着不收敛的问题[3]。应用多面体模型可以建立小天体附近全局有效的引力场模型,但是该方法计算效率较低[4]。通过改变球谐系数模型引力势函数的提取因子,使勒让德多项式的收敛条件得到改变,可以建立内球谐引力场模型,该模型可确保引力势函数表达式在与中心小天体相切的球体范围内收敛[5]。
轨迹优化方法主要包括基于庞特里亚金极小值原理的间接法和基于参数化方法的直接法。在间接法应用方面,文献[6]和文献[7]首先求解光滑程度较高的能量最优问题,通过引入同伦参数,将能量最优问题逐步转化为燃耗最优问题,最终得到燃耗最优轨迹。同伦方法并不能从根本上解决间接法的协态初值敏感问题,求解轨迹优化问题仍然存在一定困难。
直接法无需推导优化问题的横截条件,避免了求解两点边值问题的协态初值敏感问题,因而得到了广泛的应用。文献[8]和文献[9]在轨迹优化中考虑了动力学参数和状态不确定性的影响,分别将闭环敏感度矩阵方程和误差传播协方差矩阵引入优化指标,进而采用高斯伪谱法对轨迹优化问题进行解算。在小天体附着轨迹优化方面,直接法仍然以高斯伪谱法为主,解算过程耗时较长,并且解的精度依赖于对状态变量和控制变量的初始猜测。
凸优化算法是直接法的一种,具有形式简单,计算效率高的特点[10]。它的子类——二阶锥规划问题(SOCP),在航天器轨迹设计与优化方面得到了广泛应用[11-12]。二阶锥规划问题要求性能指标和动力学方程为线性,且约束条件满足二阶锥约束。对动力学和约束条件进行离散化以后,采取内点法[13]对参数优化问题进行求解,可以确保寻优结果能够在有限次迭代内收敛到全局最优解。
本文首先采用内球谐模型对目标小天体周围引力场进行精确建模;通过约束条件松弛、动力学方程线性化、动力学和约束条件离散化,将小天体附着多约束轨迹优化问题转化为一个可以迭代求解的二阶锥规划问题,并通过内点法进行解算;最后以216 Kleopatra[14]小行星为目标小天体,对上述过程进行仿真求解,以校验算法的可行性和有效性。
1 小天体附着动力学模型
1.1 内球谐引力场模型
引力场建模是研究和分析小天体附近运动行为的基础,本文采用内球谐引力场模型对小天体周围引力场进行精确建模,内球谐坐标系下引力加速度的表达式为[5]:
(1)
(2)
(3)

(4)
式中:xi,yi,zi分别为内球谐坐标系下探测器的位置信息。内球谐引力系数可以通过最小二乘法进行采样估计,计算式为:
(5)
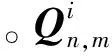
(6)
g可以通过任意已知的引力场模型计算得到,例如多面体模型[4]、质子群模型[15]等。为了确保式(5)为一个满秩系统,数据点个数Ndata应该至少为n2+2n个。内球谐系数确定以后,由式(1)~(3)可以快速求出内布里渊球内任意点的引力加速度。所构造内布里渊球应该与小天体表面的目标着陆点相切,球心选取应保证探测器下降轨迹包含在内布里渊球内部。
1.2 动力学方程及坐标转换
定义小天体固连坐标系如下:坐标原点o位于小天体的质心,z轴沿小天体自旋轴方向,x轴沿小天体最小惯量轴方向,y轴满足右手系法则。在小天体固连坐标系下,探测器的附着动力学方程可以写为:
(7)

探测器附着动力学方程是在小天体固连系下推导得到,而内球谐引力场模型的引力加速度解算是在内球谐坐标系进行的,两者之间需要进行坐标转换。为了简化计算,可以令内球谐坐标系的三个坐标轴xi,yi,zi分别与小天体固连坐标系的x轴、y轴、z轴平行,如图1所示。此时,两个坐标系间的转换关系为:
ri=r-Δr
(8)
式中:Δr表示内球谐坐标系原点与小天体质心之间的位置矢量差。
2 小天体附着轨迹优化方法
本节首先建立小天体附着多约束轨迹优化方程,进而通过约束条件松弛、动力学方程线性化、动力学和约束条件离散化,将原始轨迹优化问题转化为一个可以迭代求解的二阶锥规划问题,并通过内点法进行解算。
2.1 小天体附着轨迹优化问题描述
探测器应该满足如下的边界条件:
(9)
式中:r0和v0为探测器在初始时刻的位置和速度,m0表示探测器初始时刻的质量,rt为目标着陆点,vt为终端速度约束,对于软着陆问题,vt=0。此外,探测器推力应该满足如下控制约束:
(10)
式中:Tmax为发动机推力最大值。以燃耗作为优化指标,可以表述如下:
(11)
式中:tf为附着所需时间。
优化指标(11),动力学方程(7),边界约束(9)及控制约束(10)构成小天体附着燃耗最优轨迹优化方程。
2.2 序列凸优化算法

(12)

(13)
松弛后的优化问题可以写为:

minJT,Γ=∫tf0Γdτ s.t. r=v=-2ω×v-ω×(ω×r)+g+Tm=-ΓIspger(0)=r0v(0)=v0m(0)=m0r(tf)=rfv(tf)=03×1T2x+T2y+T2z≤Γ0≤Γ≤Tmaxìîíïïïïïïïïïïïïïïïïïï(14)

二阶锥规划问题要求系统的动力学方程必须是线性的,所以需要对式(14)中的微分方程组进行线性化处理。定义一组新变量如下:
(15)
将以上变量代入式(14)。此时,动力学方程为:
(16)
边界约束条件为:
(17)
控制约束条件为:
(18)
式中:p0(t)=ln(m0-Tmaxt/Ispge),优化指标可以写为:
(19)
通过以上线性化过程,优化变量从[T,Γ]转换为[u,σ],从而消除了原动力学方程中分母变量m带来的非线性问题。

其中,
(20)
式(20)中各矩阵定义为:
其中,uk,σk, ▽Vk分别表示u,σ, ▽V在时间节点tk时刻的值。离散化后的轨迹优化问题可以概括如下:

minJuk,σk=∑Nk=0σk s.t. X0=[rT0,vT0,p0]TMXN=[rTf,01×3]Tuk≤σk0≤σk≤Tmaxe-p0(tk)[1-(pk-p0(tk))]ìîíïïïïïï(21)
式中:M=[I6,06×1],k从0取到N。经过离散化处理以后,微分方程约束被转化为代数方程约束。原来的轨迹优化问题转换为一个离散的参数优化问题。
式(21)中的终端状态XN需要由式(20)递推得到。递推过程中,需要求解每个时间节点处的引力加速度信息,通常情况下,引力加速度是关于位置r的非线性函数,这使得式(21)不是一个标准的二阶锥规划问题,不能直接采用内点法进行求解。为此,本文采用一种迭代算法来进行优化问题解算,即首先假设引力加速度为一个常量,例如▽V0,此时式(21)成为一个二阶锥规划问题,采用内点法可以得到此时的最优轨迹;以得到的轨迹作为参考轨迹,由式(1)~(3)计算该轨迹上每个时间节点的引力加速度值,再代入式(21),采用内点法进行求解,得到一条新的轨迹,将得到的新轨迹作为下一次迭代的参考轨迹;经过多次迭代,直到轨迹收敛,即前后两次迭代得到的优化轨迹之差小于某一个固定值ε,从而得到小天体附着燃耗最优轨迹。以上每次迭代过程,都需要求解一次二阶锥规划问题,这种迭代算法也被称作序列凸优化算法。
3 仿真结果及分析
本节以216 Kleopatra小行星为目标小天体进行仿真分析,以校验算法的可行性和有效性。216 Kleopatra小行星尺寸约为217×94×81 km,光谱类型为M类。216 Kleopatra小行星多面体模型如图2所示,仿真参数设置如表1所示。

时间x/my/mz/mvx/(m·s-1)vy/(m·s-1)vz/(m·s-1)m/kgt=0-1501086010-1034100500t=tf-1126006340-12520000-
根据探测器的初始位置和目标着陆点,构造包含附着轨迹的内球谐引力场模型。采用多面体模型作为参考,阶次n选为30,所构造内球谐引力场模型误差分布如图3所示。从图3可以看出,误差由内布里渊球球心沿半径方向逐渐增大,最高不超过6%,可以满足轨迹优化精度需求。
小行星216 Kleopatra的自旋角速度为3.2411×10-4rad/s,发动机比冲Isp=300 s,推力幅值Tmax=100 N,仿真时间tf=1000 s,离散时间节点N=500。采用序列凸优化算法,进行轨迹优化解算,内点法由Matlab环境下的MOSEK[16]软件实现,令ε=0.3 m,则经过四次迭代以后,轨迹最终收敛,优化轨迹如图4所示。优化得到的末端时刻探测器的质量为479.9 kg,即消耗燃料20.1 kg。
探测器推力矢量大小随时间变化曲线如图5所示。可以发现,推力大小满足最优控制的bang-bang控制形式,推力变化大概可以分为三个阶段,在前期,发动机处于饱和状态实现对探测器动力加速;在中间阶段,将发动机关闭,令探测器自由运动,达到节省燃料消耗的目的;在最终阶段,发动机全开提供反向推力,实现探测器的软着陆。在发动机工作的时段,总推力的大小基本保持在100 N,即发动机在点火工作时处于最大推力状态,只是推力方向不断变化。
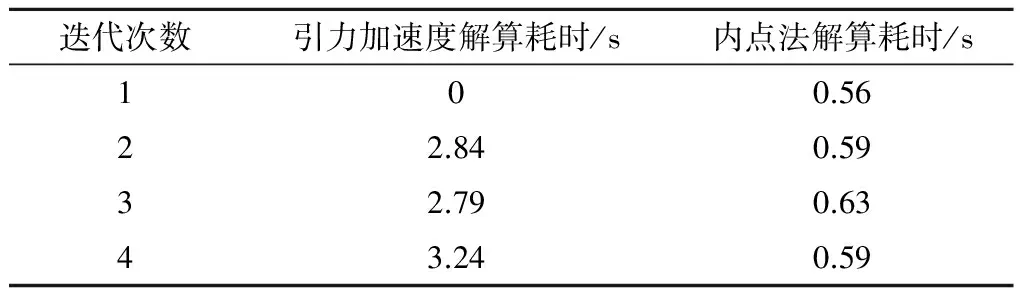
迭代次数引力加速度解算耗时/s内点法解算耗时/s100.5622.840.5932.790.6343.240.59
每次迭代引力加速度估计和优化耗时如表2所示。由于内球谐引力场模型为幂级数形式,避免了求解线积分和面积分的过程,使得计算效率较多面体模型有了极大地提升。此外,将原始轨迹优化问题转换为二阶锥规划问题以后,形式简单,求解快速,尽管增加了迭代过程,但总耗时仅为11.24 s。
为了进一步验证凸优化算法在轨迹优化计算效率方面的优势,采用高斯伪谱法进行对比分析,离散节点个数N同样设为500。高斯伪谱法采用Matlab环境下的GPOPS-II软件实现[17],两种方法沿x方向的优化轨迹如图6所示。由图6可知,高斯伪谱法优化轨迹与序列凸优化轨迹几乎吻合,优化得到的末端时刻探测器的质量同为479.9 kg,高斯伪谱法的优化用时达到了32830.49 s。仿真结果表明,本文所采用的序列凸优化算法可以在不降低优化性能的前提下,极大地提升小天体附着轨迹优化问题的求解效率。
4 结束语
本文针对小天体附着多约束轨迹优化问题,提出了一种基于序列凸优化的轨迹优化算法。首先采用内球谐引力场模型,对形状不规则的小天体进行引力场精确建模;通过约束松弛、线性化和离散化处理,将小天体附着多约束轨迹优化方程转换为一个可以迭代求解的二阶锥规划问题,并由内点法得到燃耗最优轨迹。数学仿真结果显示,采用序列凸优化算法得到的附着轨迹以零速度到达预定着陆点,符合各项约束条件,并实现燃耗最优的目标。
[1] 崔平远, 乔栋. 小天体附近轨道动力学与控制研究现状与展望[J]. 力学进展, 2013(5): 526-539. [Cui Ping-yuan, Qiao Dong. State-of-the-art and prospects for orbital dynamics and control near small celestial bodies[J]. Advances in Mechanics, 2013(5): 526-539.]
[2] 崔平远, 袁旭, 朱圣英, 等. 小天体自主附着技术研究进展[J]. 宇航学报, 2016, 37(7): 759-767. [Cui Ping-yuan, Yuan Xu, Zhu Sheng-ying, et al. Research progress of small body autonomous landing techniques[J]. Journal of Astronautics, 2016, 37(7): 759-767.]
[3] Scheeres D J, Williams B G, Miller J K. Evaluation of the dynamic environment of an asteroid: applications to 433 Eros[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(3): 466-475.
[4] Werner R A, Scheeres D J. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy, 1996, 65(3): 313-344.
[5] Takahashi Y, Scheeres D J, Werner R A. Surface gravity fields for asteroids and comets[J]. Journal of Guidance, Control, and
Dynamics, 2013, 36(2): 362-374.
[6] Ren Y, Shan J J. Reliability-based soft landing trajectory optimization near asteroid with uncertain gravitational field[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(9): 1810-1820.
[7] Yang H, Baoyin H. Fuel-optimal control for soft landing on an irregular asteroid[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1688-1697.
[8] 胡海静,高艾,朱圣英,等. 考虑跟踪制导的小天体着陆轨迹闭环优化方法[J]. 宇航学报, 2015, 36(12): 1384-1390. [Hu Hai-jing, Gao Ai, Zhu Sheng-ying, et al. Closed-loop trajectory optimization for precision landing on small bodies considering tracking guidance[J]. Journal of Astronautics, 2015, 36(12): 1384-1390.]
[9] Hu H, Zhu S, Cui P. Desensitized optimal trajectory for landing on small bodies with reduced landing error[J]. Aerospace Science and Technology, 2016, 48: 178-185.
[10] Liu X, Lu P, Pan B. Survey of convex optimization for aerospace applications[J]. Astrodynamics, 2017, 1(1): 23-40.
[11] Acikmese B, Ploen S R. Convex programming approach to powered descent guidance for Mars landing[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1353-1366.
[12] Blackmore L, Acikmese B, Scharf D P. Minimum-landing-error powered-descent guidance for Mars landing using convex optimization[J]. Journal of guidance, control, and dynamics, 2010, 33(4): 1161-1171.
[13] Nesterov Y E, Todd M J. Self-scaled barriers and interior-point methods for convex programming[J]. Mathematics of Operations Research, 1997, 22(1): 1-42.
[14] Descamps P, Marchis F, Berthier J, et al. Triplicity and physical characteristics of asteroid (216) Kleopatra[J]. Icarus, 2011, 211(2): 1022-1033.
[15] Park R S, Werner R A, Bhaskaran S. Estimating small-body gravity field from shape model and navigation data[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 212-221.
[16] Andersen E D, Roos C, Terlaky T. On implementing a primal-dual interior-point method for conic quadratic optimization[J]. Mathematical Programming, 2003, 95(2): 249-277.
[17] Patterson M A, Rao A V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software, 2014(41): 1.
