基于增量调制的ICCP地磁匹配序列生成方法
2018-03-16段修生齐晓慧
段修生,肖 晶,齐晓慧
(1. 石家庄铁道大学机械工程学院,石家庄 050043;2. 陆军工程大学石家庄校区无人机工程系,石家庄 050003)
0 引 言
地磁导航是一种基于地理信息的导航方式,相比卫星导航和地形导航等方式,地磁导航具有无源、无辐射、隐蔽性强、误差不随时间积累等特点,且能够进行全天候、全地域导航[1],是修正惯导系统(Inertial navigation system, INS)累积误差的一种有效方式。匹配算法是地磁匹配导航系统的核心,是影响导航精度和效率的关键因素。地磁匹配算法的基本原理是对一段时间内积累的地磁测量序列与预先存储在计算机中的地磁基准图进行相关计算,进而得到载体的位置,其实质是通过一定方法确定INS指示航迹与载体真实航迹之间的空域变换关系[2]。地磁匹配算法可分为轮廓匹配(Contour matching, CM)算法[3-4]和迭代最近等值线点(Iterated closest contour point, ICCP)匹配算法[5-6]。两者的不同之处在于,CM算法构造了一个纯平移的变换模型来求解空域变换,认为INS只存在位置误差;而ICCP算法考虑了匹配过程中的速度误差和航向误差,将地磁匹配模型简化为一个以刚性变换为基础的仿射变换模型,因此仿射变换模型更接近实际系统中测量航迹与真实航迹间的复杂变换。
寻找最近点的效率是影响ICCP算法实时性的关键[6],这不仅与算法的搜索空间、搜索策略等因素相关,还与匹配序列的长度相关。如果增加匹配序列的长度,算法的搜索时间会成倍增加。为提高ICCP算法的性能,学者们从搜索空间、搜索策略等多个方面进行了改进。例如,ICCP算法为了在地磁图上找到与磁场测量值最接近的等值线,往往要遍历整个磁场区域,Liu等[7]和Komiya等[8]分别通过设置滑动窗口和优化搜索空间缩小了算法的搜索范围;此外,蚁群优化算法(Ant colony optimization, ACO)[9]、遗传算法(Genetic algorithm, GA)[10]等智能搜索策略也被引入ICCP算法以提高算法性能。这些改进措施中匹配序列的获取都建立在等间隔采样的基础上[3, 5]。
然而,采样间隔设置不合理会增大匹配误差,甚至导致匹配失败。地磁场是弱磁场,主磁场以平缓变化为主,地面上1000 km以下的水平面内地球主磁场总强度的变化率仅为0.02~0.03 nT/m[11],加之变化场和载体自身磁场的影响,磁场测量的真实值很可能被淹没,即使是局部变化较为丰富的地磁异常场,这个问题也不能忽视。虽然地磁测量误差补偿可以有效降低环境磁场的影响,但补偿后的余差和磁传感器的测量噪声仍可能导致磁场测量值混淆而无法匹配[12-13]。此外,如果采样间隔较小,匹配序列各位置对应的磁场变化也小,由于不同载体装载的磁传感器的分辨率各不相同,如果磁传感器无法分辨匹配序列中的磁场变化,匹配算法依然无法进行。从这个角度看,匹配序列中采样间隔的设置是有效匹配的前提,需要相关理论进行指导。
另一方面,序列长度是生成匹配序列必须设置的一个参数。有学者建议用地磁序列的自相关系数下降到1/e(e=2.718)时对应的位移量作为匹配长度设置的参考,但对实际应用的指导意义不大[14]。实际上,影响序列长度的因素很多,很难在理论上给出统一的建模方法。为了解决算法精度和实时性之间的矛盾,有学者提出了逐点迭代匹配[14]和实时迭代评价的估计方法[15],其基本思想都是在每一步迭代求解后判断算法匹配结果是否满足所设准则,并以此确定匹配序列的长度。因此,可以将匹配序列长度等参数的设置问题转化为优化问题求解:将判定准则转化为解析形式的目标函数,并选择合适的优化算法,则可通过匹配仿真试验得到统计意义下的最佳匹配参数。
本文以飞行器地磁匹配导航为研究背景,利用通信理论中增量调制的方法指导地磁匹配序列中匹配点的选取,并通过BPSO算法对序列长度等参数进行优化,提出了一种基于增量调制的ICCP地磁匹配序列生成方法,该方法可依据不同的磁场信息调节匹配序列长度。
1 基于增量调制的地磁匹配序列生成
1.1 生成匹配序列的约束条件
载体运动轨迹上地磁场的测量值可视为一条包含了不同频率成分的信号。为保证匹配序列对应的磁场值能够完整地保留载体航迹上的磁场信息,匹配点的选择首先需要满足采样定理,即:
fs≥2fmax
(1)
式中:fs是采样频率。对载体航迹上的磁场信号进行傅里叶变换,则fmax可根据其能量谱确定。
图1是一条典型航路上磁场信号傅里叶变换的能量谱。由图1可知,地磁信号的能量主要集中在低频,这意味着采样周期Ts(Ts=1/fs)的取值不能太大。本文取fmax及之前的频率成分的能量总和不小于磁场信号总能量的96%。
地磁图的精度也会影响匹配序列的选择。局部高精度地磁图的获取通常有两种方法:实地测量法[16-17]和地磁模型插值法[18-19],所得磁图多以网格形式保存在导航计算机中。考虑到不能在同一个网格内重复采样,相邻两个匹配点的距离应大于等于一个磁图网络对应的距离,即:
(2)
式中:Ts为采样周期,d为地磁图网格间距,v为载体的运动速度,ng为载体一个采样周期内经过的磁图网格数。
为了避免由磁场起伏不太明显和磁传感器测量精度限制等因素导致的地磁测量值的混淆,还应该考虑匹配序列中相邻点的磁场变化:只有当地磁测量序列某一点与匹配序列前一个点的磁场变化不小于规定阈值时,该点才会被加入到匹配序列中,即:
FPi-FPi-1≥δ
(3)
式中:FPi为匹配序列中Pi点对应的磁场强度测量值,δ为所设阈值,对应增量调制的量阶。
1.2 地磁匹配序列的生成
增量调制用一位二进制码表示信号的变化,规则简单且利于实现,可用于指导生成匹配序列。其基本思想为:在载体航迹规划阶段依据INS积累误差的特性及背景磁场的特点选择若干校正点进行地磁匹配以对INS进行校正,在满足约束条件(1)和(2)的情况下,对航迹上磁场测量值进行增量调制,选择磁场变化满足所设量阶的位置构成匹配序列。
记载体运动过程中磁传感器输出的地磁场测量信号为F(t),量化后的阶梯地磁曲线为F′(k),则:
F′(k)=F′(k-1)+sgn[F(kTs)-F′(k-1)]δ
(4)
式中:δ为增量调制的量阶,Ts为采样周期。函数sgn(x)的定义为:
(5)
设调制后的地磁序列为FC(k),则基于增量调制规则对F(t)的编码过程可以描述为:
(6)
图2为利用增量调制原理对某一航迹的磁场测量信号进行编码的示意图。
依据增量调制规则,量阶为δ时,地磁场测量信号F(t)被编码为“010111111000”的序列。当编码序列中连续出现两个“1”或“0”,即式(7)成立时,表明对应采样时刻的磁场变化超过了所设量阶,条件(3)满足。此时,取当前采样时刻对应的INS输出位置作为地磁匹配序列中的一个元素,如图中的Pi(i=1, 2, …, 7)点。依此类推,当匹配序列积累到一定长度时,再利用ICCP算法进行匹配,逼近地磁匹配序列对应等值线上的最近点序列。
FC(k)⊕FC(k-1)=0,k=2,3,…,n-1
(7)
式中:n为序列FC的长度,“⊕”为异或运算符号。
基于增量调制生成匹配序列的过程实质上是一种变间隔采样策略。对于起伏较大、信息丰富的磁场区域,如果等间隔采样所得的匹配序列上磁场变化大于量阶δ,则等间隔采样所得的匹配序列与基于增量调制的匹配序列完全相同,此时前者可视为后者的特例;在磁场起伏相对平缓的区域,增量调制的采样间隔为等采样间隔的整数倍。
1.3 匹配序列长度的影响
设m1为磁传感器等间隔采样获得的磁场测量序列,m2为相应采样时刻地磁图的读图值,序列长度为N,则m1,m2中对应元素之差Δm可以表示为:
Δm=m1-m2
(8)
假设εm是大于Δm中每个元素的绝对值的一个较小的数,记作|Δm|<εm,根据Ingemar[20]的理论,εm越小,则两磁场序列越相似,误匹配的概率越高。
若m1,m2服从高斯分布,则关于Δm的联合概率密度函数可以表示为:
(9)
式中:N为匹配序列长度,C为Δm的协方差矩阵。
对C进行特征分解:
C=UΛUT
(10)
式中:U为特征向量矩阵,Λ为对角阵,对角线上的元素为C对应的特征值。
用变量替换法,设Δm=Uy,代入式(9)进行解相关计算,整理得到:
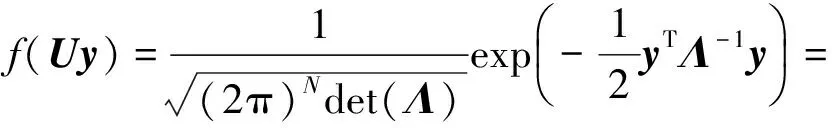
(11)
式中:y中各元素yi(i=1,2,…,N)是相互独立的高斯随机过程,λ为C的特征值。
根据y与Δm的关系,可以构造一个P(|Δm|≤εm)的上界:
P(|Δm|≤εm)≤P(|y|≤ε)=
(12)
式中:ε不小于εm。
若协方差阵C正定,则λi>0,进而:
(13)
结合式(12)和式(13)可知,地磁误匹配的概率随匹配序列长度的增加而降低。由于等间隔采样时序列长度的增加等价于匹配距离的增加,因此更确切地讲,误匹配概率随着匹配距离的增加而降低。由于任何非高斯分布的函数都可由若干高斯分布函数的和无限逼近,因此m1,m2不服从高斯分布时这一结论也成立。
然而,当匹配距离增加到一定程度时,匹配算法精度改善有限,而时间代价大大增加;另一方面,匹配距离还受采样频率、载体运动特性和INS性能等因素的影响,难以像地磁匹配序列与误匹配关系一样在理论上精确建模。此外,虽然ICCP算法假设磁传感器无测量误差,但实际应用中为了避免各采样时刻的磁场测量值因噪声影响而导致匹配失败,量阶的设置除了考虑航迹上磁场的变化情况,还应考虑地磁补偿后的噪声水平。
2 基于BPSO的匹配序列的参数优化
由上述分析可知,基于增量调制生成地磁匹配序列一共需要确定两个参数:匹配序列长度L和量阶δ。本文避开了匹配序列长度复杂的建模过程,对L和δ进行联合优化,寻找两者在一定条件下的最佳组合,这样,不同航迹上不同校正点处的量阶和匹配序列长度会随着规划航迹上磁场的变化而调整,增强了算法对磁场环境的适应性。
2.1 参数优化的原理及流程
BPSO是一种离散的群智能优化算法,原理简单且收敛速度快。本文结合BPSO算法给出量阶δ和匹配序列长度L的一种估计方法,其流程见图3。
如图3所示,首先,在载体航迹规划阶段可依据INS的误差积累特性和导航区域的磁场信息选择若干校正点对INS的积累误差进行校正。在每一个校正点处,分别确定参数δ和L的搜索范围并对其进行二进制编码。然后,选择合适的目标函数,并在所设参数范围内利用BPSO算法进行寻优,找到使目标函数值最小的粒子,该粒子所在位置即为所求解。最后,对最优解进行解码即可得所设校正点处δ和L的最佳值。
以下对几个关键问题进行说明:
1)δ和L搜索范围的确定及编码
根据增量调制的原理,对于磁场起伏较大的航迹,量阶δ的取值应该适当增大;当磁场起伏较小时,δ应适当减小。本文依据地磁异常模型NGDC-720中磁场的变化情况,当δ在1 nT至15 nT之间取值时,可以满足实际需求。
根据ICCP算法原理,当L≥3时算法才能进行,因此设L搜索范围的最小值为3。L搜索范围的最大值对应校正点之前的航迹取δ范围内的最大值生成的匹配序列的长度。
举例说明δ和L的编码过程:设δ在1 nT至7 nT之间取值,L∈[3, 30],则δ需要三位编码,L需要五位,算法的搜索范围为[00011001, 11110111],其中,前五位代表L,后三位代表δ。
2)目标函数的建立
本文参数优化问题的目标函数f(x)为:
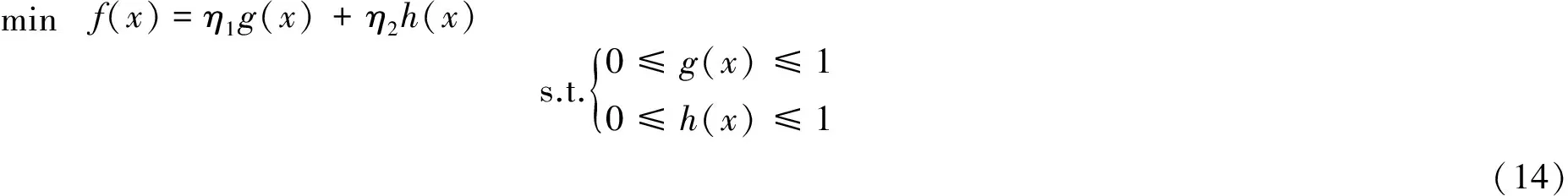
minf(x)=η1g(x)+η2h(x)s.t.0≤g(x)≤10≤h(x)≤1{ (14)
式中:x为决策解,对其进行解码可以得到最佳匹配序列长度L和量阶δ;函数g(x)为用本文方法生成的序列进行匹配的位置误差的归一化函数,h(x)为算法平均迭代一次所用时间的归一化函数,g(x)和h(x)的取值范围都为[0, 1]。η1,η2为可调因子,调节匹配精度与匹配时间的比重。优化目标为在搜索空间内确定合适的匹配序列长度L和量阶δ,使函数f(x)取值最小。
对g(x)和h(x)进行归一化处理主要是为了消除量纲的影响。函数归一化的方法有很多,本文采用较为简单的线性归一化方法。以g(x)为例,其归一化函数定义为:
(15)
式中:x1,x2是归一化函数的两个端点,依据实际应用中地磁图网格的精度及导航系统对算法精度的要求而定。本文取x1为1个地磁图网格对应的距离,x2为2个地磁图网格对应的距离。h(x)与g(x)的定义类似,不再赘述,对应端点依据对实时性的要求而定。不失一般性,文中分别取x1=0.5 s,x2=2 s。
3)算法的终止条件
算法的终止条件为:在连续几次迭代中目标函数的取值变化都在较小的范围内或达到所设的最大迭代次数。
上述方法具有以下特点:(1)直接以匹配精度和时间为基础构建优化目标函数,保证了算法的性能;(2)以航迹上校正点之前的磁场测量值为基础生成匹配序列,而不是从该点开始积累匹配序列,提高了算法的效率;(3)各校正点处的参数可在航迹规划阶段离线计算,而在任务执行阶段直接调用,进一步保证了算法的时效性。
2.2 基于NGDC-720模型的参数优化算例
以地磁异常场模型NGDC-720为数据源,随机选择经纬度范围分别为[54.8°, 56.8°]N,[45.0°, 47.0°]E的磁场区域,记作区域一,通过Kriging插值法建立精细化模型作为背景磁场,如图4所示,磁场网格的分辨率为250 m。在区域内随机生成若干航迹, 对匹配序列长度及增量调制的量阶进行设计。图中还标出了三条路径代表航迹上的磁场变化,“*”为所选的校正点。
以区域一的路径一为例,由于区域一磁场变化比较剧烈,可将δ和L的搜索范围适当扩大以保证匹配精度。因此,路径一上δ和L的搜索范围分别设置为[1 nT, 15 nT]和[3, 31];BPSO优化算法中种群数目设为30,迭代次数设为100,图5为该航迹在不同δ和L下目标函数的取值。
图5中,利用增量调制原理生成的地磁匹配序列进行匹配时,不同δ和L下的匹配精度和时间不同,因此目标函数的取值各不相同。从变化规律看,虽然δ和L较小时匹配算法用时较少,但相应匹配距离较短,算法的精度无法保证,目标函数取值较大;当δ和L增加到一定程度后,目标函数取值较小,且在最小值处,匹配算法能够在保证匹配精度的基础上减小匹配时间。对于区域一的路径一,当δ=15 nT,L=22(图中小旗所在位置)时,目标函数取到最小值1.41,说明在路径一的校正点处选择该组参数生成匹配序列可以获得较好的匹配效果。
3 仿真校验
3.1 无磁场测量噪声时各方法的比较
以区域一的路径一为例,假设载体沿规划航迹以35m/s的速度做等高匀速直线运动,到达校正点时INS的积累误差为790 m。分别用本文方法和等间隔采样生成的地磁匹配序列进行比较,其中本文方法的量阶δ及匹配序列长度L采用BPSO算法的优化值,等间隔采样的时间间隔按条件(1)和条件(2)的约束设置为24 s。为了提高最近点搜索的效率,依据INS误差的统计特性将ICCP算法的搜索范围设置在±3σ以内[15],其中,σ为INS自上次更新以来所产生的漂移。匹配误差按下式计算:
(16)
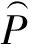
设匹配算法迭代次数为300,当相邻两次迭代的匹配误差的变化量小于1 m时,迭代终止,输出匹配结果。图6为路径一上不同方法的匹配结果图。
图6 (a)为不同匹配序列的匹配结果。将航迹末端的图像放大,见图6 (b),其中,INS指示航迹上符号“△”为当前时刻INS的指示位置,规划航迹上“□”为当前时刻载体规划的位置。由图6可知,由于INS的误差积累,在当前时刻载体位置已有较大偏差,基于增量调制原理和等间隔采样获得的匹配序列在地磁等值线的约束下,收敛到各匹配点磁场测量值对应等值线上的最近点序列,证明了本文方法的有效性。就匹配结果看,基于增量调制的ICCP算法的校正结果更接近载体的规划航迹,校正效果优于相同匹配距离的等间隔采样ICCP算法。从参与匹配的序列看,等间隔采样的匹配序列匹配点较多且均匀分布,而基于增量调制的匹配序列考虑了各匹配点对应的磁场变化,匹配点较少且非均匀分布。
为衡量各匹配序列的匹配效果,图7给出了不同方法在迭代过程中的匹配误差和对应匹配序列上磁场的变化。图7(a)中,三种算法都能减小INS的积累误差。匹配序列长度相同时,等间隔采样的匹配序列和基于增量调制的匹配序列平均迭代一次所用的时间相当,分别为1.64 s和1.87 s;前者的匹配误差为665.30 m,后者的匹配误差为267.97 m。对比图7(b)可知,此时基于增量调制的匹配序列能够利用较多的磁场信息参与匹配,保证了算法的精度。匹配距离相同时,等间隔采样的匹配序列平均迭代一次所用的时间为27.21 s,而基于增量调制的匹配序列耗时为1.87 s,这是因为增量调制方法控制了匹配序列间磁场的起伏变化,能够用较短的序列进行匹配,提高了算法的效率。此外,相同匹配距离时基于增量调制的ICCP算法的匹配精度也较高。
在区域一内随机生成若干条航迹进行匹配,仿真条件及载体的运动规律等保持不变,表1给出了匹配结果。
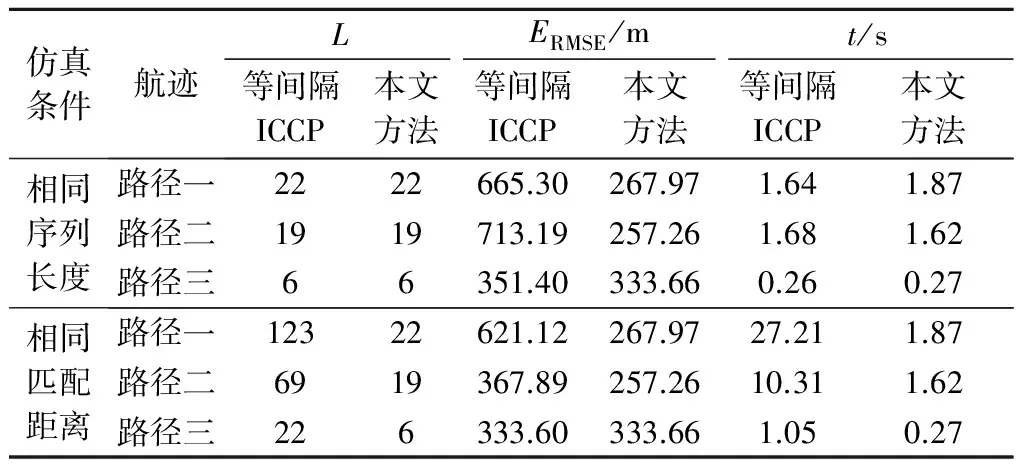
表1 区域一不同条件下算法的比较Table 1 Comparison of algorithms under different conditions in area 1
当匹配序列长度相同时,从匹配误差看,所有航迹上本文方法的匹配误差均小于等间隔采样的ICCP算法,且在路径一和路径二上,本文方法的匹配结果远优于等间隔采样的ICCP算法;从算法的执行时间看,等间隔采样的ICCP算法与基于增量调制的ICCP算法迭代一次的时间相当。对等间隔匹配序列而言,当匹配序列长度增加时,匹配结果有所改善,但相应匹配时间也增加。匹配距离相同时,一般来说两种算法匹配精度相当,有些情况下本文算法性能更好。但本文算法的突出优势是匹配序列更短,实时性大大提高。例如表中路径一上,基于增量调制生成匹配序列对匹配算法时间压缩非常明显。仿真试验还表明,基于增量调制的匹配序列一般不需要太长即可获得较好的结果。
3.2 有磁场测量噪声时各方法的比较
考虑磁传感器有测量噪声的情况,假设磁场测量噪声服从均值为0 nT,方差为5的高斯分布[12], 其他的仿真条件及载体的运动规律等保持不变,对各种序列生成方法进行比较。图8给出了路径三在不同条件下的匹配误差。由图8可知,虽然地磁测量值含有噪声,但各方法对INS的积累误差还有一定的校正作用。匹配结束后,本文方法的匹配误差为381.51 m,与其相同匹配序列长度的等间隔采样ICCP算法的匹配误差为465.99 m,与本文方法相同匹配距离的等间隔采样ICCP算法的误差为566.83 m。与表1不考虑磁场噪声的情况相比,各方法匹配精度都有所下降,但本文方法受噪声影响最小,而相同匹配距离的等间隔采样匹配序列的匹配效果最差。
3.3 磁场起伏不明显区域各方法的比较
为验证所提序列生成方法在磁场起伏不明显的区域的匹配性能,在NGDC-720异常场模型上随机挑选一块经纬度范围分别为[33.8°, 35.8°]N,[15.0°, 17.0°]E的区域,记作区域二。通过Kriging插值建立该区域的精细化模型,模型分辨率依然为250 m。表2给出了区域一和区域二的几个统计特征。可见,区域二的磁场起伏比较平缓。

表2 磁场的几个统计特征Table 2 Several statistical features of two magnetic areas
以区域二的路径一为例,首先利用BPSO算法离线估计其在校正点处生成匹配序列所需的量阶δ和匹配序列长度L。区域二磁场起伏较小,可适当减小搜索范围以避免匹配的距离过长。本文设δ和L的搜索范围为[1, 8]和[3, 10]。BPSO算法的种群数目和迭代次数保持不变。当δ=7 nT,L=7时,目标函数取值最小。之后考虑是否含有磁场测量噪声,用不同方法生成匹配序列,并在多条航迹上进行匹配,表3、表4给出了两条航迹的匹配结果。

表3 无磁场测量噪声时不同条件下各方法的比较Table 3 Methods comparison under different conditions when no magnetic noise exists
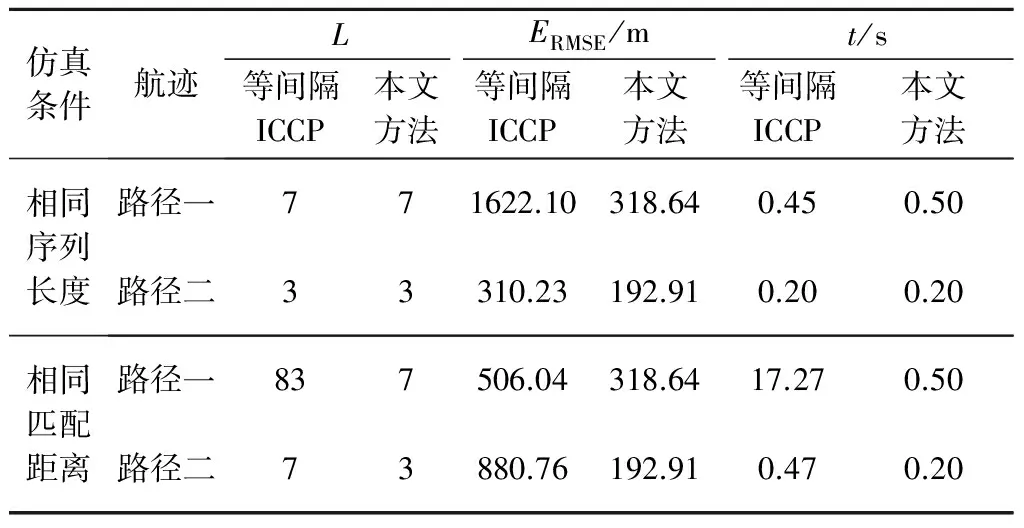
表4 含磁场测量噪声时不同条件下各方法的比较Table 4 Methods comparison under different conditions when magnetic noise exists
表3的路径一上,相同匹配序列长度的等间隔采样ICCP算法匹配误差为784.53 m,几乎无法修正INS的积累误差。这主要是因为区域二磁场总体起伏较小,等采样间隔获取的匹配序列磁场变化也较小,可利用的磁场信息有限,要提高匹配精度,只能增加匹配距离;匹配距离较长的等间隔采样ICCP算法和基于增量调制的ICCP算法取得了更好的匹配结果,匹配误差分别为161.65 m和159.92 m。表中其他航迹上基于增量调制的匹配序列的误差均小于等间隔采样生成的匹配序列,且匹配序列长度相同时,两种方法执行一次迭代的平均时间相当。增加匹配序列长度时,等间隔采样ICCP算法的匹配结果有所改善,但时间代价太大;基于增量调制的匹配序列由于长度更短,匹配消耗的时间更少,且匹配结果也不低于等间隔采样的ICCP算法。
表4中,区域二磁场的总体起伏比较小,因此只加入了均值为0 nT,方差为0.5的测量噪声以保证有效匹配。从各方法消耗的时间看,基于增量调制的匹配序列与相同匹配序列长度的等间隔采样序列平均迭代一次用时相当,而比相同匹配距离的等间隔采样序列所用时间更短。例如路径一上,基于增量调制的匹配序列迭代一次用时0.50 s,而相同匹配距离的等间隔采样匹配序列为17.27 s,可见本文方法具有显著优势。从匹配精度看,路径一相同序列长度时等间隔采样ICCP算法和路径二相同匹配距离时等间隔采样ICCP算法的匹配结果已无法修正INS积累误差(预设积累误差为790 m),而本文方法依然能够有效匹配,说明其在磁场起伏不太明显的区域也具有较好的适应性。
综上所述可得以下结论:1)当匹配距离相同时,本文算法所用匹配序列的长度更短,大大缩短了匹配时间;当匹配序列长度相同时,本文算法与等间隔ICCP算法耗时相当,但由于本文算法匹配距离更长,因此本文算法匹配精度提高明显。2)无论有无磁场噪声,基于增量调制的ICCP地磁匹配算法性能都优于等间隔ICCP算法,并且在含噪声的情况下,基于增量调制的ICCP算法优势更明显。3)本文算法可依据背景磁场信息自适应调整生成匹配序列所需的参数,可在保证算法精度的基础上尽量降低时间消耗。
4 结 论
本文提出了一种基于增量调制的ICCP地磁匹配序列生成方法,通过设置合理的目标函数将匹配序列长度等参数的设计问题转化为优化问题求解,使地磁匹配序列能够依据规划航迹的磁场信息及导航系统对精度和实时性等要求进行调整,以适应不同的应用背景。试验证明了所提方法的可行性和有效性,即使在磁场起伏不太明显的区域及磁传感器有测量噪声时,该方法也具有良好的适应性。
[1] 郭才发, 胡正东, 张士峰, 等. 地磁导航综述[J]. 宇航学报, 2009, 30(4): 1314-1319. [Guo Cai-fa, Hu Zheng-dong, Zhang Shi-feng, et al. A survey of geomagnetic navigation [J]. Journal of Astronautics, 2009, 30(4): 1314-1319.]
[2] Lin Y, Yan L, Tong Q X. Underwater geomagnetic navigation based on ICP algorithm[C]. The 2007 IEEE International Conference on Robotics and Biomimetics, Sanya, China, December 15-18, 2007.
[3] Wu Z T, Hu X P, Wu M P. An experimental evaluation of autonomous underwater vehicle localization on geomagnetic map [J]. Applied Physics Letters, 2013, 103 (10): 9-18.
[4] Han Y, Wang B, Deng Z, et al. An improved TERCOM-based algorithm for gravity-aided navigation [J]. IEEE Sensors Journal, 2016,16 (8): 2537-2544.
[5] Song Z G. The improved ICCP algorithm based on procrustes analysis for geomagnetic matching navigation[C]. International Conference on Design, Manufacturing and Mechatronics, Wuhan, China, April 17-18, 2015.
[6] Wang S, Lu Z, Zhang J, et al. Evaluation of ICCP algorithm for geomagnetic navigation based on hardware-in-the-loop simulation [J]. Journal of Beijing University of Aeronautics & Astronautics, 2015, 41 (2):187-192.
[7] Liu M, Wang B, Deng Z, et al. Improved ICCP algorithm and its application in gravity matching aided inertial navigation system[C]. Chinese Control Conference, Nanjing, China, July 28-30, 2014.
[8] Komiya K, Miyashita S, Maruoka Y, et al. Control of autonomous mobile robot using map matching with optimized search range [J]. Electrical Engineering in Japan, 2015, 190(4): 66-75.
[9] 王跃钢, 贾磊, 单斌, 等. 自适应SA-ACO地磁匹配导航算法[J]. 中国惯性技术学报, 2014, 22(1):89-93. [Wang Yue-gang, Jia Lei, Shan Bin, et al. Adaptive SA-ACO geomagnetic matching navigation algorithm [J]. Journal of Chinese Inertial Technology, 2014, 22(1): 89-93.]
[10] 朱占龙, 杨功流, 王艳永, 等. 一种基于自适应遗传搜索策略的地磁匹配算法研究[J]. 测控技术, 2014, 33(6): 146-149. [Zhu Zhan-long, Yang Gong-liu, Wang Yan-yong, et al. Research on geomagnetic matching algorithm based on adaptive genetic searching strategy [J]. Technology of Measure and Control, 2014, 33(6):146-149.]
[11] 梁莹. INS/地磁匹配组合导航系统技术研究[D]. 哈尔滨:哈尔滨工程大学, 2010. [Liang Ying. Research on technologies of INS/Geomagnetic matching integrated navigation System [D]. Harbin: Harbin Engineering University, 2010.]
[12] Ge Z, Liu S, Li G, et al. Error model of geomagnetic-field measurement and extended Kalman-filter based compensation method [J]. PLoS ONE, 2017, 12(4): e 0173962.
[13] Liu Z, Zhang Q, Pan M, et al. Compensation of geomagnetic vector measurement system with differential magnetic field method [J]. IEEE Sensors Journal, 2016, 16(24): 9006-9013.
[14] 刘颖, 曹聚亮, 吴美平. 无人机地磁辅助定位及组合导航技术研究[M]. 北京:国防工业出版社, 2016: 32-37.
[15] 黄斌, 孙永荣, 王丽娜, 等. 地磁导航的迭代评价匹配算法[J]. 南京航空航天大学学报, 2012, 44(4):565-569. [Huang Bin, Sun Yong-rong, Wang Li-na, et al. Iterative evaluation matching algorithm for geomagnetic navigation [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(4):565-569.]
[16] 赵塔, 朱小宁, 程德福, 等. 水下地磁导航技术中的地磁场空间差分测量方法[J]. 吉林大学学报(工学版), 2017, 47(1):316-322. [Zhao Ta, Zhu Xiao-ning, Cheng De-fu, et al. Geomagnetic field spatial difference measuring method for underwater geomagnetic navigation technology [J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 316-322.]
[17] Wang P, Hu X P, Wu M P. Matching suitability analysis for geomagnetic aided navigation based on an intelligent classification method [J]. Journal of Aerospace Engineering, 2014, 228 (2): 271-283.
[18] 李明明, 黄显林, 卢鸿谦,等. 基于矩谐分析的高精度局部地磁场建模研究[J]. 宇航学报, 2010, 31(7):1730-1736. [Li Ming-ming, Huang Xian-lin, Lu Hong-qian, et al. Modeling of high accuracy local geomagnetic field based on rectangular harmonic analysis [J]. Journal of Astronautics, 2010, 31(7): 1730-1736.]
[19] Zhao Y, Chang S, Li W, et al. Boundary compensation approach in geomagnetic map preparation based on BEMD [J]. Earth Science-Journal of China University of Geosciences, 2014, 39 (11):1617-1624.
[20] Ingemar N. Terrain navigation for underwater vehicles using the correlator method [J]. IEEE Journal of Oceanic Engineering, 2004, 29 (3): 906-915.
