液体圆柱射流在气流中的破碎特性实验研究

邓 甜, 蒋 帅, 高绪万

(中国民航大学, 天津 300300)

0 引 言

从低污染排放航空发动机燃烧室技术的发展方向可以看出，燃油直接射入预混预蒸发装置从而与空气充分混合形成混合油气进而燃烧是未来的研究重点，这就要求研究燃油在空气气流流动中的破碎、雾化、蒸发以及油气混合程度，其中，对液体射流破碎数学模型的研究能够为燃烧室设计提供参考。近年来，液体射流在横向气流中破碎的研究方式主要为射流破碎机理的研究以及射流破碎特性无量纲参数与相关物理参数之间的数值关系研究。在科技没有很发达之前主要采用阴影法等基础光学方法对横向气流中的射流破碎特性进行研究[1]。射流破碎的初始破碎是研究雾化的基础内容，这部分内容的研究会直接决定二次雾化模型的精确度与准确性。Wu P.K.等人[2]通过实验研究对横向气流中射流破碎的机理进行了归纳与分析，得出了较为翔实的实验结论，总结了破碎过程中射流破碎的不同机理，包括加强毛细力破碎、袋式破碎、复合破碎以及剪切力破碎。Samir等人[3]则把表面波分解为毛细管型与加速度波型。这些研究都把横向气流中射流的破碎与由空气气动力所产生的表面波联系了起来。

对于横向气流射流的穿透深度也得到了很多学者的重视与研究。Schez等人[4]通过理论分析认为对于最大穿透深度发生所在的位置而言，应该要使得射流液柱在气动力的作用下将原有的动量方向转换90°直到其方向与横向气流的方向一致。他还通过实验研究得到了射流穿透深度是6.25倍喷嘴孔径的结论，通过大量实验对比，Schez认为射流液柱的穿透深度与液气动量比应该也存在着某种关联。Lubarsky等人[5]则通过实验认为射流的穿透深度与射流的雷诺数存在指数关系。总的说来，目前国内外学者对于穿透深度经验公式的拟合尚存在较大区别，表1总结了学者们在文献中拟合的数学关系式[6-14]。

1 实验装置及条件

本文采用的射流破碎实验台，如图1所示，分为气源、液源、观测实验段、图像处理和喷嘴等。实验中的气源系统为空压机以及与之相连的高压气罐，气罐内储存空压机产生的0.8MPa高压空气。液源由高压储液罐以及与之相连的压缩空气构成的，通过将压缩空气通入储有液体水的液罐中，实现储液罐内高压环境，在压力的作用下，液体水通过管道被压入喷嘴，达到液体射流的目的。喷嘴为直射式，其孔径为1mm，长径比为20。实验中观测段是四面为有机玻璃的通道，横向气流从上游进入；观测段下游下为喷嘴入口，喷嘴安装方向为竖直方向。观测段下游区域同时装有风速计，用来测量横向气流的流速；高压液罐出口处安装流量计，用来测量液体射流流量。图像采集系统包含高速相机、图像采集处理计算机以及光源3个部分。本文采用IDT公司的NX3-S4型号高速相机，其最大分辨率(1280pixel×1024pixel)时最高帧率为3750fps。实验工况如表2所示，表中下标j代表射流，g代表横向气流。

表1 穿透深度关系式拟合结果表Table1 Penetration result summary

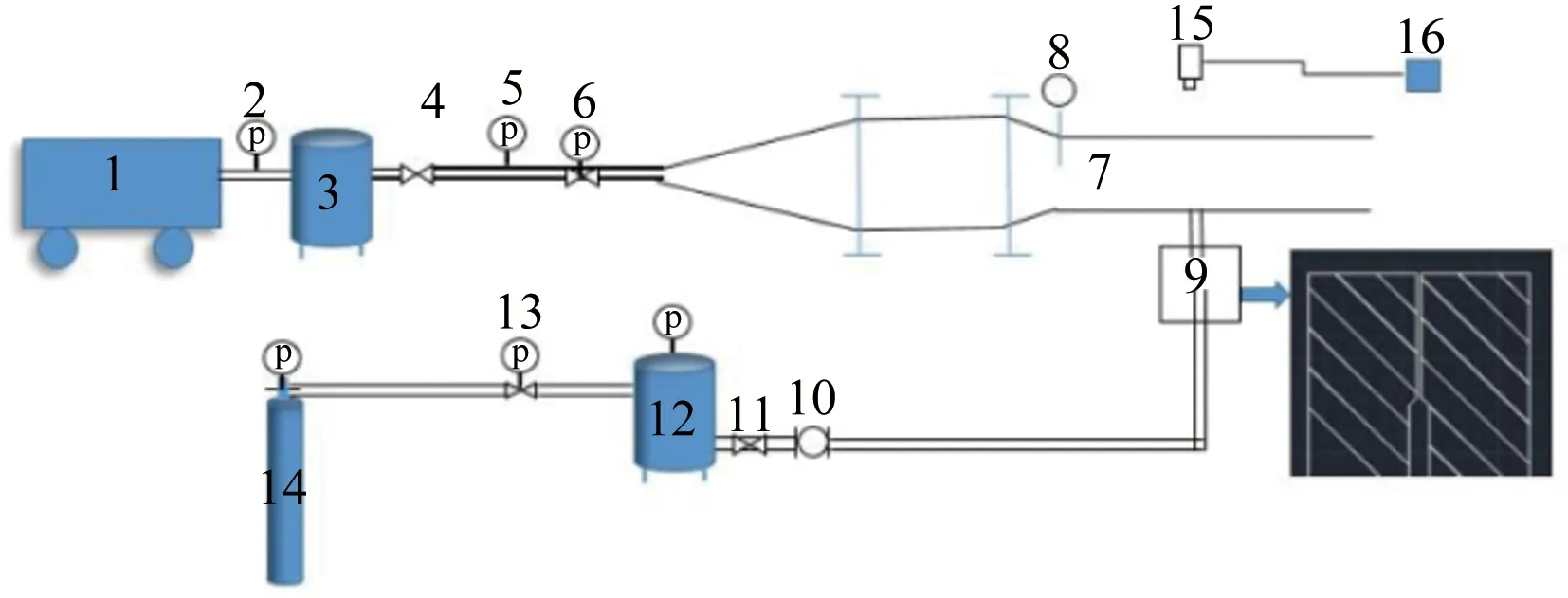
1. 空压机; 2. 压力计; 3. 储气罐; 4. 截止阀; 5. 压力计; 6. 减压阀; 7. 观测段; 8. 风速计; 9. 喷嘴; 10. 流量计; 11. 截止阀; 12. 压力储液罐; 13. 减压阀; 14. 高压气罐; 15. 高速相机; 16. 处理计算机

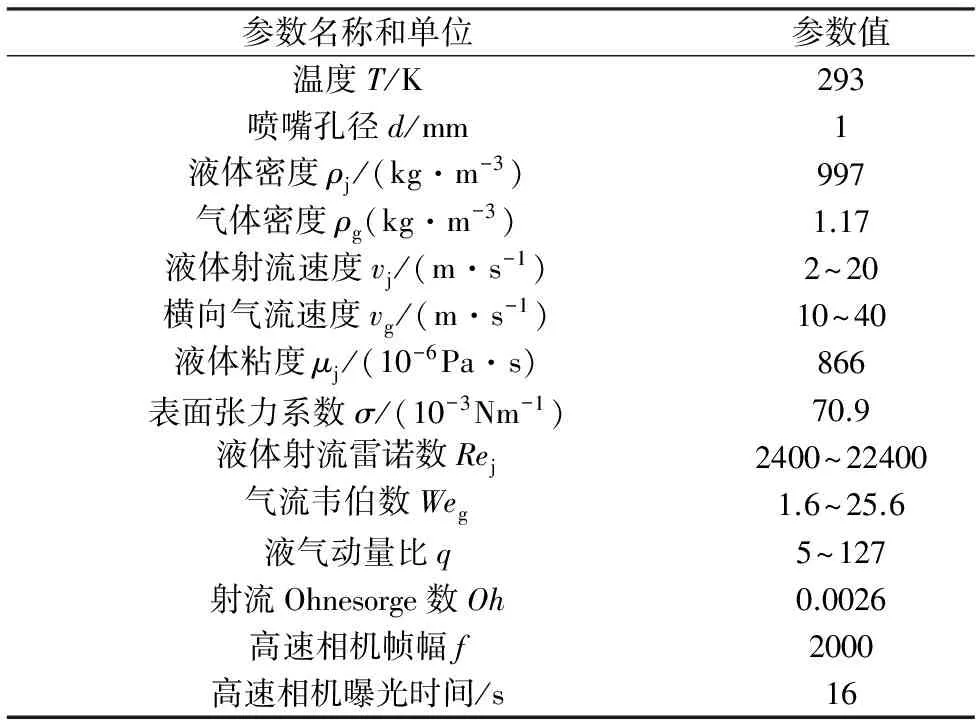
表2 实验工况及参数设置Table 2 Experimental parameters

2 实验结果与分析

本文对表2中的每个工况进行10次实验，然后对物理量取平均，并用这些均值进行相关数学关系式拟合，而对于图片分析则采用10张图中物理量与均值最接近的1张作为该工况下的实验结果图。定义射流方向为y方向，横向气流方向为x方向，液体射流主液柱首次断裂产生第1颗液滴的位置为破碎点，如图2所示。

2.1 表面波发展趋势

射流液柱的发展与破碎的根本原因是表面波的存在与发展，因此对表面波进行定性与定量的分析是建立射流破碎物理模型的基础。

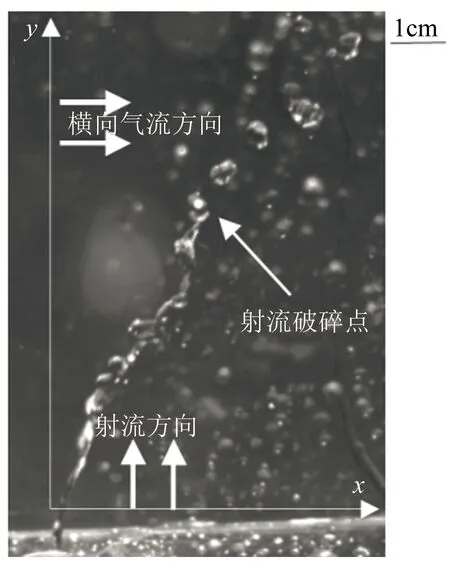
图2 射流相关参数定义

图3是4张连续拍摄到的射流液柱图，射流速度vj为5m/s，气流速度vg为25m/s，气流韦伯数Weg为10，液气动量比q为34，其图片采集顺序依次为a、b、c、d，时间间隔为0.0005s。

从图3可以发现，射流从喷嘴中喷出后的最开始一段距离内，其表面比较光滑，且并未发现有表面波现象。随着射流在横向气流中的发展，液柱表面开始出现抖动，且能够观察到小振幅的蛇形波现象。这种蛇形波极其不稳定，在横向气流的作用下不断发展，呈现出螺旋流动状态。在表面张力的继续作用下，液体向着波峰位置汇聚，并最终断裂破碎，产生液滴。为了进一步研究表面波与液滴的产生过程，图4对射流液柱进行局部放大。

图4中可以看出，液体射流在横向气流中的发展过程中所剥离出的大液滴的尺寸是喷嘴孔径的3.5倍左右，与文献[15]对比，其液滴尺寸为无横向气流时液滴尺寸的2倍，证明了在横向气流中的射流液柱的表面波作用更为强烈，其可以将更多的液体汇聚到波峰处，产生尺寸较大的液滴。液柱破碎产生大液滴的同时也会产生部分小液滴，这些小液滴产生的机理与无横向气流时射流液柱破碎产生液滴及“卫星液滴”机理相似，但是不同之处在于，横向气流中液柱破碎产生的“卫星液滴”会在横向气流的作用下继续向下游发展，而不是与大液滴汇聚后继续向下游发展。液柱在横向气流的作用下，其迎风面和背风面受力不一致，导致表面波不再是轴对称表面波，而迅速发展为高阶非轴对称表面波形式。同时在横向气流的作用下，射流液柱以一种回旋的形式向下游发展，且其不稳定性大大增加。

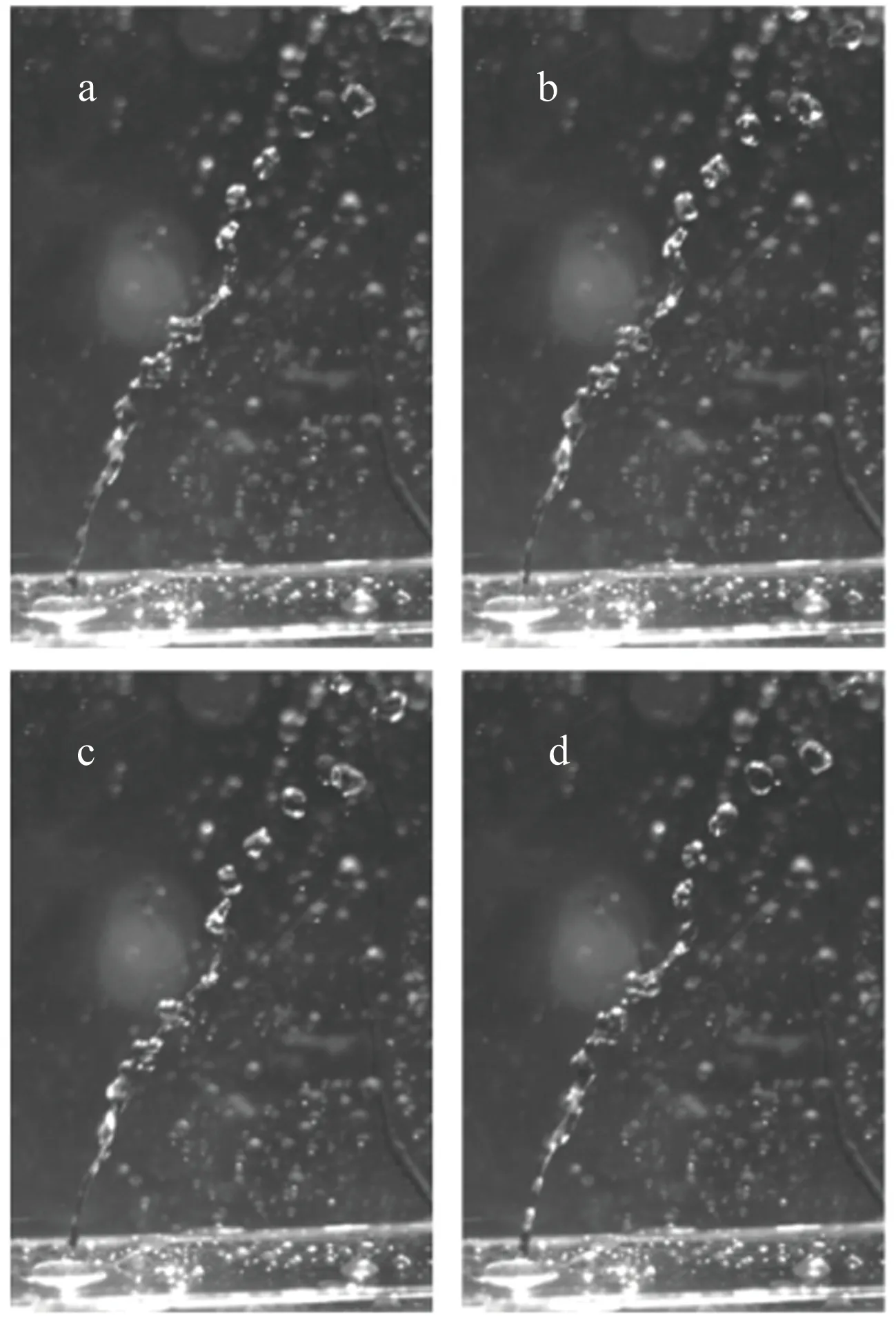
图3 射流液柱在横向气流中的发展与破碎(vj=5m, q=34)

Fig.3Developmentandbreakupofthejetinthecrossflow(vj=5m,q=34)

图4 表面波与断裂处局部放大图

下面对破碎点附近的表面波波长(表面波2个波峰之间的距离)进行定量分析，实验拍照时设置标尺并测量波长值，如图4所示。为了使分析结果更具有一般性，本文定义无量纲表面波波长，即原始波长与喷嘴孔径的比值：λ/d，研究该无量纲波长与气流韦伯数之间的关系。采用恒定液体射流速度5m/s,气流韦伯数在1.6～9之间变化，得到的实验结果如图5所示。

①比较两组治疗前与治疗3个月后房颤负荷与平均心率（HR）；②比较两组预后情况，治疗3个月后与6个月进行随访，调查永久性房颤发生率。

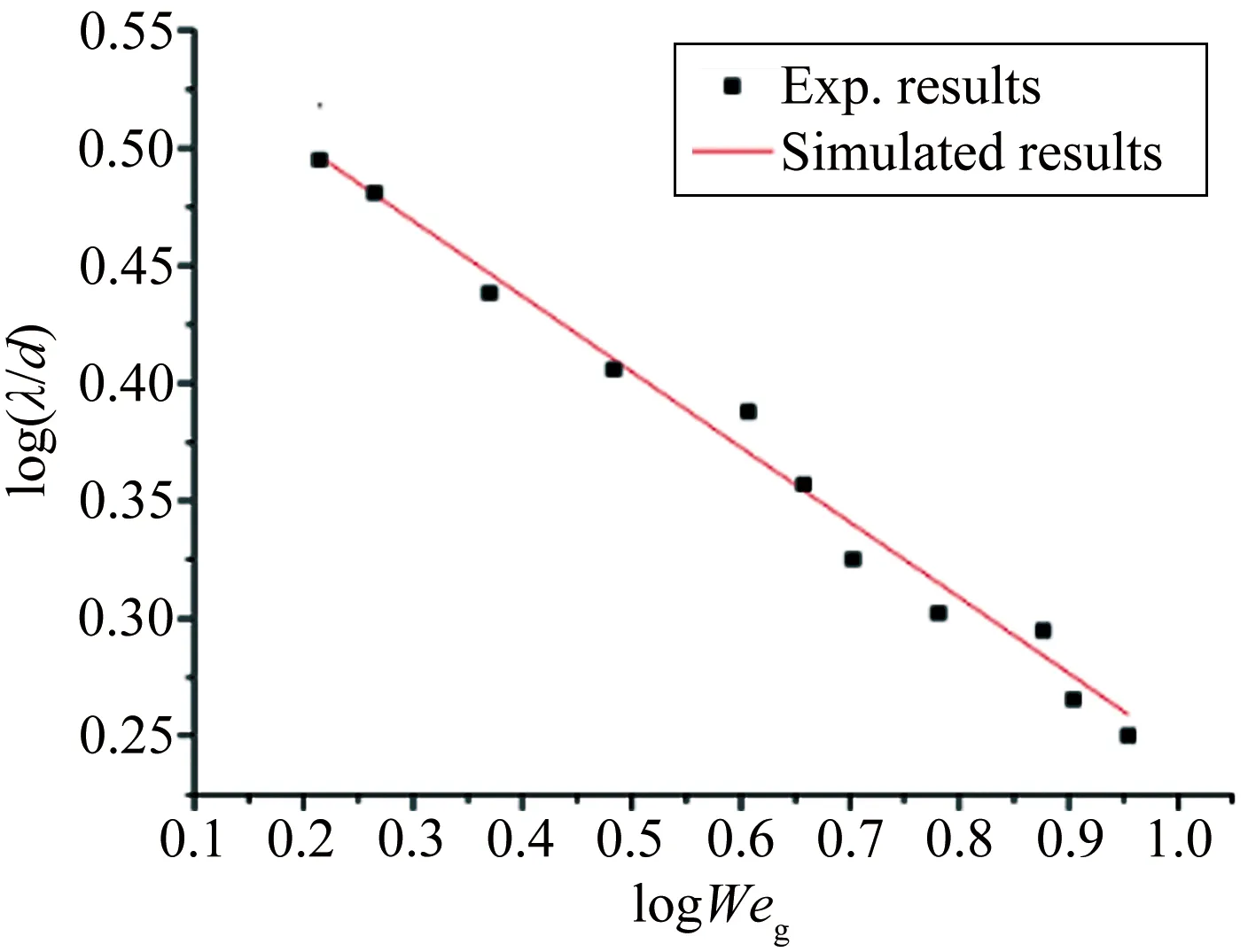
图5 无量纲表面波波长与气流韦伯数关系图

可以看到，在低韦伯数情况下，表面波的波长随着气流韦伯数的增加而减小。韦伯数的增加意味着气动力的增加，而气动力的增加会使得表面波发展更快，液柱更加不稳定，其表面波波长则会更短。相反，如果韦伯数减小，也就意味着表面张力的增加，此时气动力对液柱的影响为低频扰动，其数学关系拟合如公式(1)。

(1)

文献[16]中理论推导的指数为-0.5，比此处值更为小。而理论值是针对普遍情况下射流表面波推导而得到的，因此可以得出低气流韦伯数情况下液体射流的表面波受气流韦伯数影响更小。

2.2 射流破碎位置与发展轨迹

对于射流破碎位置与射流发展过程中流动轨迹的分析也是对横向气流中射流发展破碎模型建立的关键一步，是表征射流主液柱发生断裂的衡量工具。射流液柱破碎位置分为横向破碎位置与轴向破碎位置，如图6所示。破碎轴向距离y与破碎横向距离x分别对应了破碎点在y轴与x轴上的投影值。与无量纲波长研究类似，本部分也对无量纲破碎距离进行研究。射流液柱破碎位置主要取决于气流动量与液体射流动量之间的关系，二者相互作用，共同决定了射流的流动轨迹与射流发生破碎的位置。故研究射流轨迹以及射流破碎位置与液气动量比q之间的关系。

图6 射流液柱破碎点参数定义

破碎位置的实验结果如图7所示。下面对2个方向上的破碎距离分别进行拟合，得到如下结果。

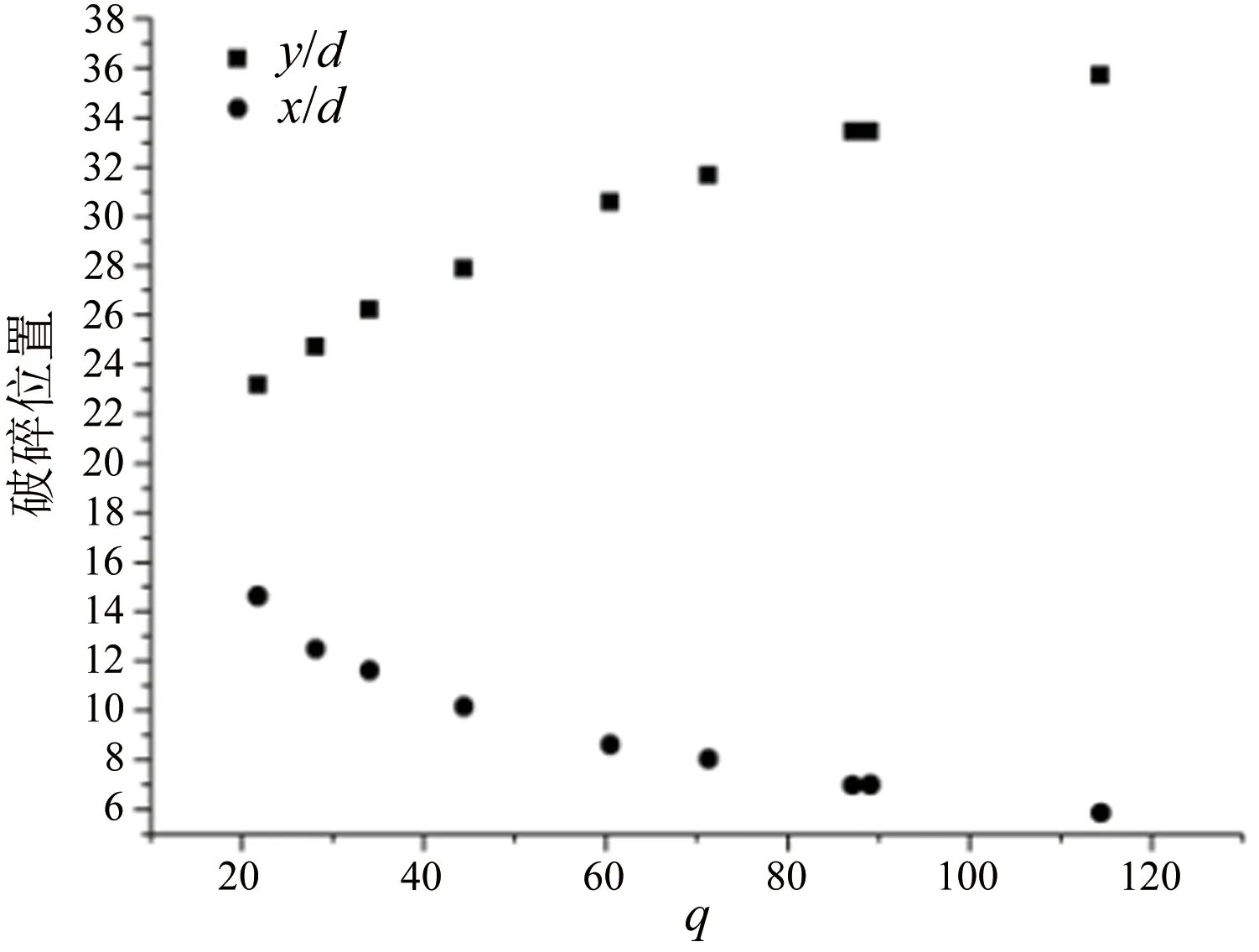
图7 无量纲破碎位置参数与q关系图

2.2.1横向破碎位置拟合

对无量纲横向破碎距离与液气动量比的关系进行拟合，如图8所示，发现前者与后者的-0.51幂指数成正比，如式(2)所示。随着液气动量比q的增加，射流的横向破碎距离减小，这是由于气动力的增加，表面产生较多的小振幅表面波，使得射流液柱不稳定增加，进而导致其在横向距离的破碎距离减小。

x/d=68.9q-0.51

(2)

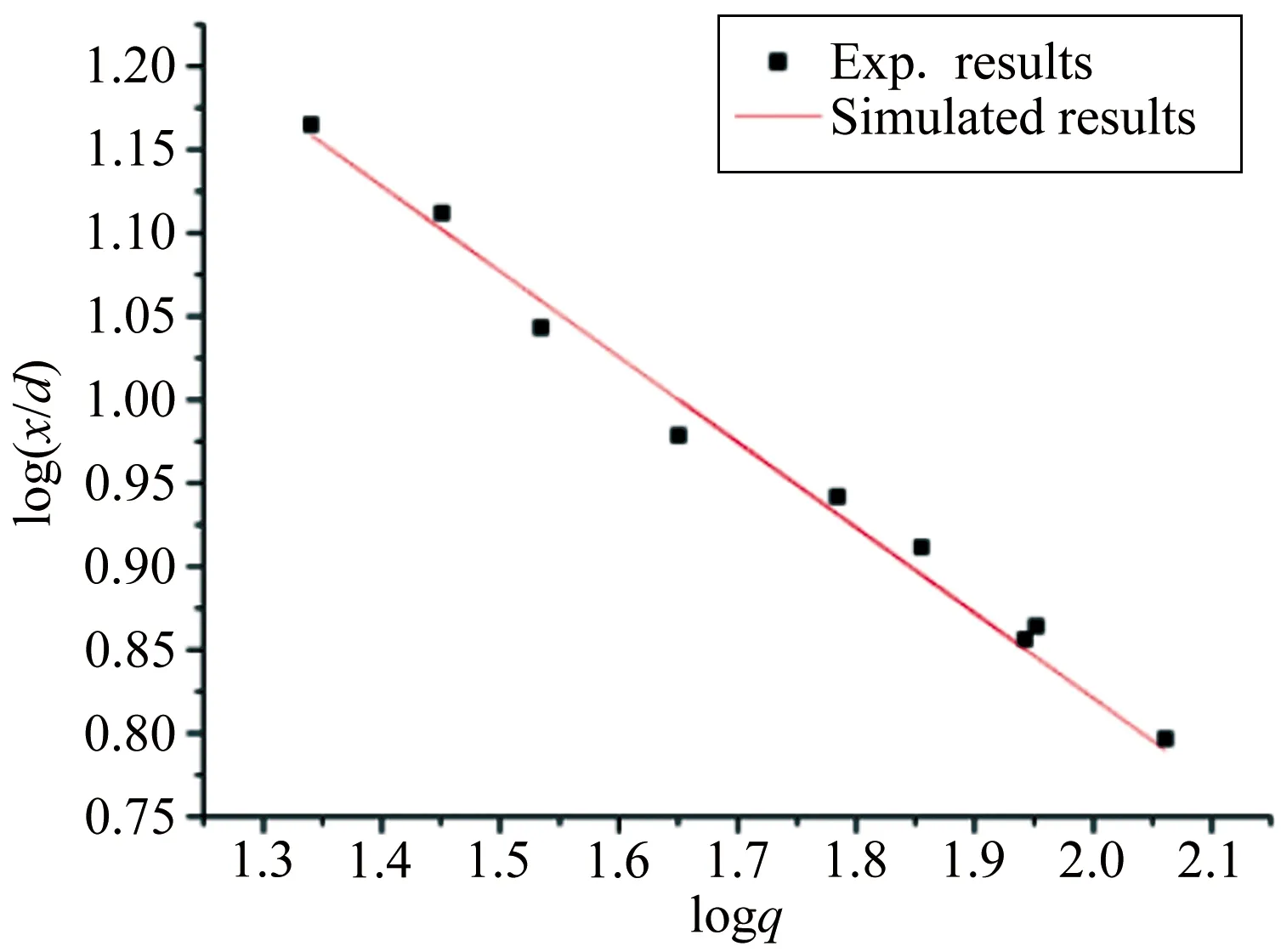
图8 无量纲横向破碎距离与液气动量比拟合关系图

Fig.8Relationbetweenthefracturepointinx-directionandthemomentumratiooftheliquidjettotheair

2.2.2轴向破碎位置拟合

轴向破碎位置与液气动量比的关系如图9所示，通过拟合得到前者与后者的0.27指数幂成正比，如式(3)所示。此处的结果与横向距离随着液气动量比q增大而减小的结果相反，这是因为随着液气动量比的增大，射流的动量足以抵抗横向气流动量，因此其在轴向的穿透距离将会随之而增加。

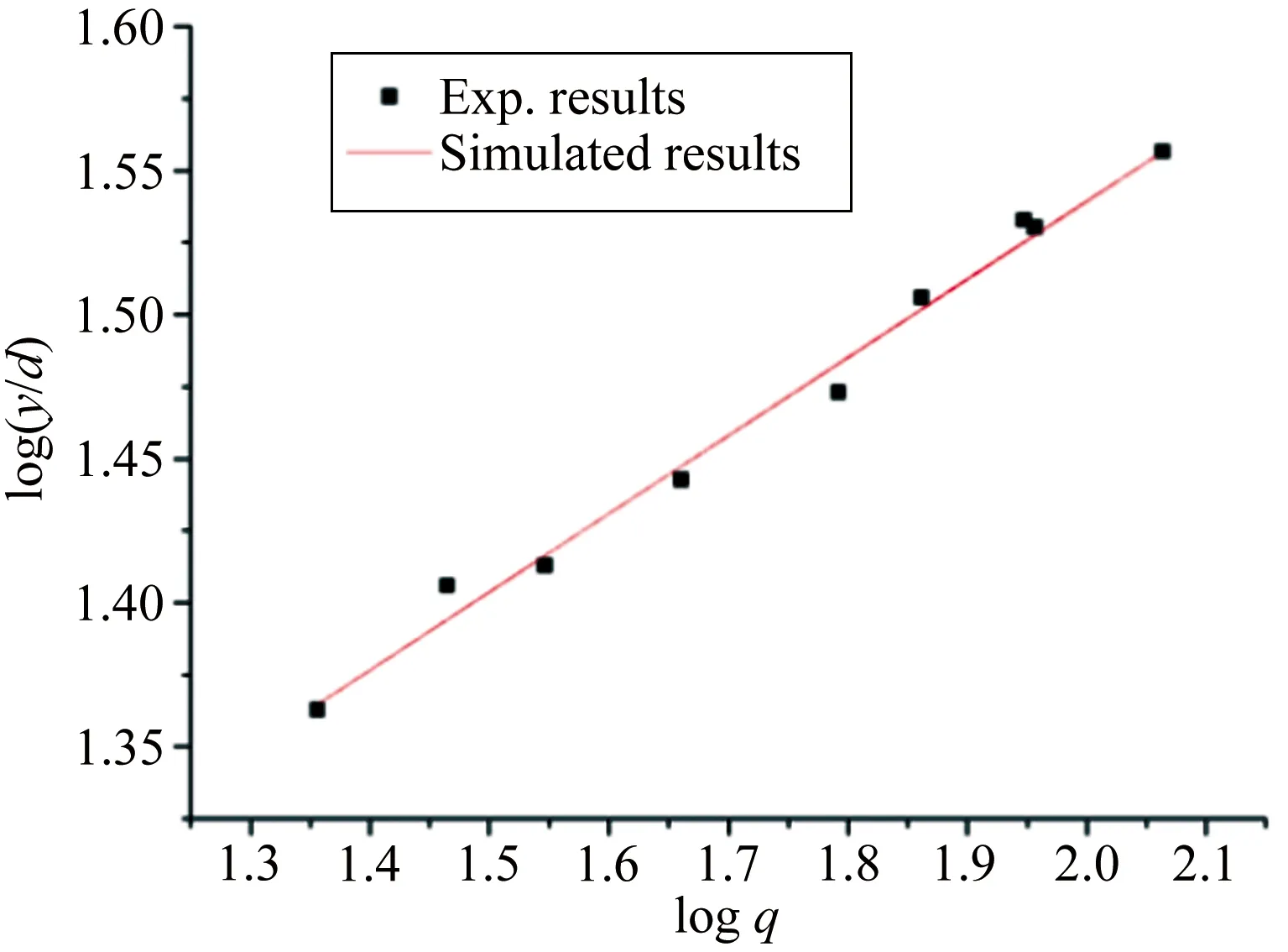
图9 无量纲轴向破碎距离与液气动量比拟合关系图

Fig.9Relationbetweenthefracturepointiny-directionandthemomentumratiooftheliquidjettotheair

y/d=9.96q0.27

(3)

2.2.3射流发展轨迹拟合

在上述破碎距离与液体动量比间关系的基础上，可以进一步推导射流的流动轨迹与液气动量比之间的近似关系。假设射流在轴向方向的速度为匀速，即该方向上的运动轨迹与时间呈线性关系，而横向方向上存在一个气动力，因此假设横向方向为加速运动，即该方向上的运动轨迹是时间的二次函数，故射流的流动轨迹应该呈现出二次函数的形式，即y/d的平方与x/d成基本线性关系。结合上面所得到的2个关系式，稍加变形与处理，可以得到射流发展过程的轨迹方程，如式(4)所示。

y/d=1.21q0.531(x/d)0.5

(4)

2.3 液柱断裂后液滴运动状态

射流液柱在低气流韦伯数下的横向气流中破碎后产生的液滴将会继续发展并破碎，因此，液滴是射流一次雾化的产物，也是二次雾化的原始形态。而往往液滴的速度将会决定二次雾化是否发生以及发生后液雾的空间分布和液雾的尺寸分布，因此对于射流一次雾化产物，即大液滴的研究将会决定二次雾化模型的精准性。下面将研究主液柱破碎后产生的液滴在横向气流中进一步发展的过程，主要研究液滴在横向气流中2个方向的速度与气流韦伯数及液气动量比之间的关系。

对于液滴速度的分析通过高速相机采集到的照片进行分析。如图10所示，a、b 2幅图采集序号已知，通过高速相机帧率便能得到时间差，经处理，可以得到2幅图中同一液滴的位置移动距离，进而便可以得到液滴在横向气流中发展的速度信息。

2.3.1液滴的轴向速度

由物理理论可知，射流射出后液柱断裂所产生的液滴速度应与射流速度类似，因此，本文首先研究该假设是否符合实验，取液柱断裂瞬间产生的液滴在原始射流方向即轴向方向(y方向)的速度v与射流初始速度vj之间的比值作为研究对象，研究该无量纲参数v/vj与气流韦伯数、液气动量比之间关系。结果如图11所示。

从图11可以看出气流韦伯数对液滴在轴向上的速度并没有太明显的影响，而受液气动量比影响较大。当液气动量比q<15时，射流液柱断裂产生的液滴的速度与射流初始速度差距较大，速度损失甚至可以达到50%。这是因为当液气动量比较小时(q<15)，横向气流动量较大，导致液柱很快发生x方向上的弯曲，这样一方面导致液体射流在横向气流的作用下受到y方向上的阻力，另一方面，液柱的弯曲也会使射流液柱在垂直y方向上的总体横截面积变大很多，导致液柱本身受到的气体阻力变大，使得液柱前锋速度损失较大，在其破碎为液滴后液滴速度自然也会降低。并且在这个阶段，无量纲轴向速度与q基本呈现一个线性关系，通过拟合，关系式如式(5)所示。

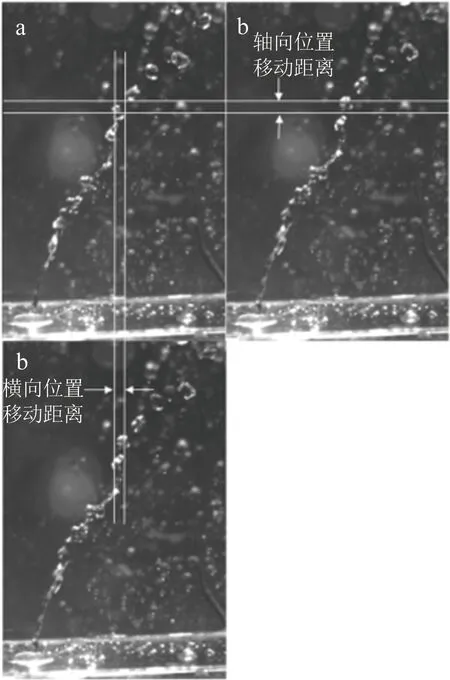
图10 液滴速度计算方法

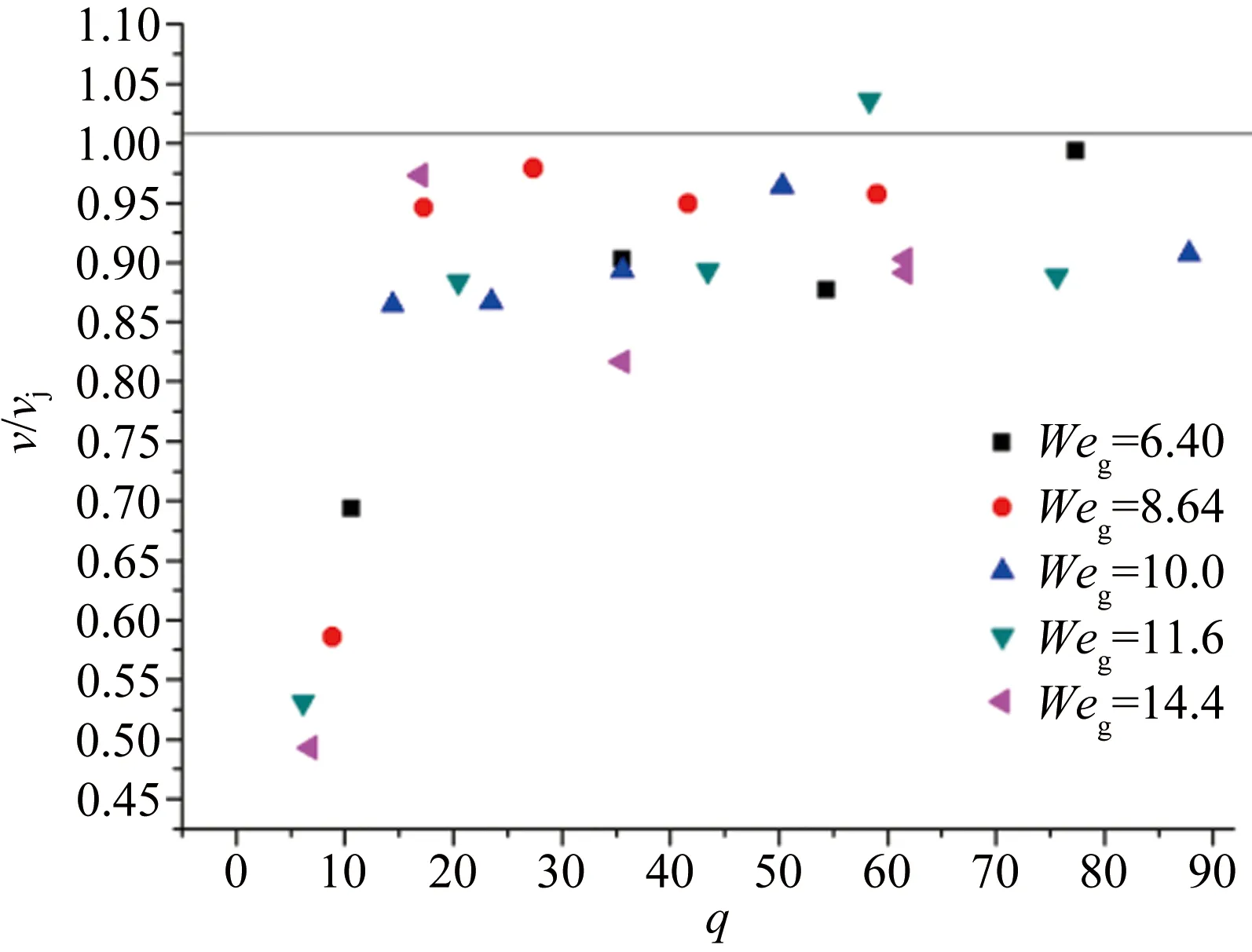
图11 液滴轴向方向速度与气流韦伯数及液气动量比的关系

Fig.11RelationshipbetweentheaxialvelocityofliquidblobandtheWebernumberoftheairwiththemomentumratio

v/vj=0.043q+0.3

(5)

当液气动量比q达到20以后，可以看到液滴在轴向上的速度总体损失不大，基本符合上文开始时候的假设，即液滴在y方向上的速度与射流初始速度近似，基本维持在0.9～1.0。

此外，从图11中也能观察到存在液滴速度甚至超过了射流初始速度的情况。研究这些情况时的照片，我们发现此时液滴在破碎前表面波恰好收缩，也就导致液滴靠近上游区域的液柱会通过表面波的形式将部分动能传递给液滴，致使液滴的速度变大。

2.3.2液滴的横向速度

类似地，研究液滴无量纲的横向速度(液滴横向速度u与气流横向速度vg的比值)与气流韦伯数和液气动量比的关系,结果如图12所示。

从图12中可以看出，断裂后的液滴在横向气流方向上的速度与横向气流的关系基本保持一致，二者的比值主要集中在0.1附近。液体射流最初并没有x方向上的速度，随着横向气流的作用，二者发生动量交换，液柱也就产生了x方向上的速度。该速度基本是由横向气流速度决定，二者的关系不随气体韦伯数与液气动量比的变化而变化。

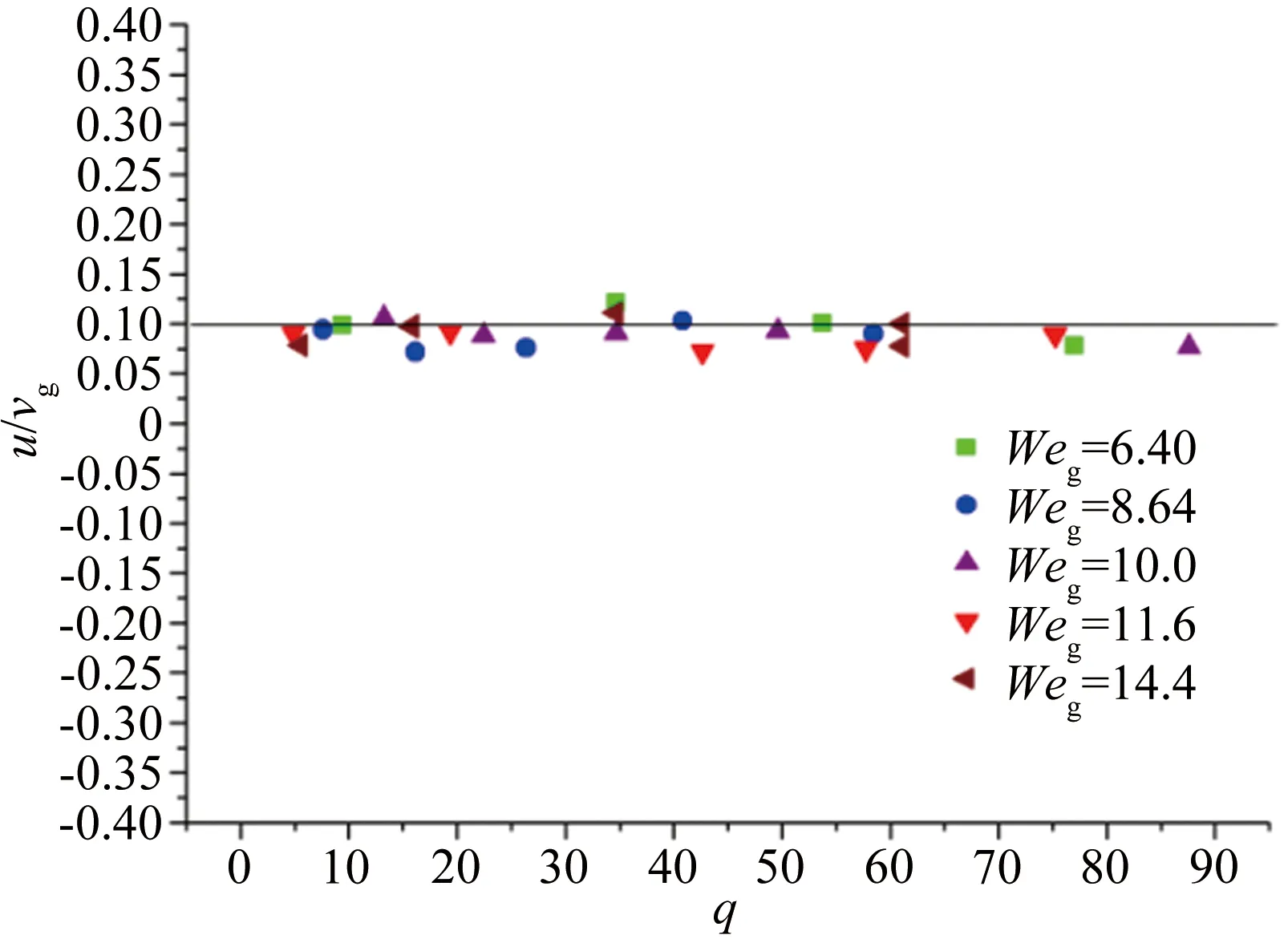
图12 液滴横向方向速度与气流韦伯数及液气动量比的关系

Fig.12RelationshipbetweentheverticalvelocityofliquidblobandtheWebernumberoftheairwiththemomentumratio

3 结 论

(1) 横向气流中，射流液柱表面的表面波与静止空气中液柱表面波发展存在差异，其一开始即已经为非对称表面波，且为高阶非对称表面波。液柱的发展呈现出回旋的形态，高度不稳定。随着表面波发展，射流发生断裂，产生出小液滴，液滴尺寸在喷嘴孔径的3.5倍左右。

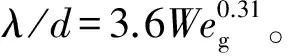
(3) 射流液柱横向破碎距离及轴向破碎距离与液气动量比之间关系分别为x/d=68.9q-0.51，y/d=9.96q0.27，射流轨迹为y/d=1.21q0.531(x/d)0.5。

(4) 对低韦伯数下液柱断裂后产生的较大尺寸的液滴进行分析，得到了其在断裂瞬间的速度信息。该速度在轴向方向上存在一个临界液气动量比值(q=15)，当q小于15时，该方向上无量纲速度与q成线性关系；当q大于15，该方向上无量纲速度基本稳定在0.8～0.9之间，且与气流韦伯数无明显关系。而该速度在横向气流方向上，与液气动量比和气体韦伯数之间也没有明显关系，基本维持在横向气流速度的0.1倍左右。

[1]Ashgriz N, Yarin A L, Yarin A L, et al. Handbook of atomization and sprays[M]. Springer US, 2011: 79-80.

[2]Wu P K, Kirkendall K A, Fuller R P, et al. Breakup processes of liquid jets in subsonic crossflows[J]. Journal of Propulsion & Power, 2015, 13(1): 64-73.

[3]Samir T, San-Mou J, Hukam M, et al. Liquid jets in subsonic crossflow[C]. AIAA Aerospace Sciences Meeting and Exhibit, 2005,2(1): 34-37.

[4]Schetz J A, Ranger A A. Aerodynamic shattering of liquid drops[J]. AIAA Journal, 1969, 7(2): 285-290.

[5]Lubarsky E, Shcherbik D, Bibik O, et al. Fuel jet in cross flow-experimental study of spray characteristics[M]. Advanced Fluid Dynamics, 2012: 176-177.

[6]Bellofiore A, Cavaliere A, Ragucci R. Air density effect on the atomization of liquid jets in crossflow[J]. Combustion Science & Technology, 2007, 179(1): 319-342.

[7]Ragucci R, Bellofiore A, Cavaliere A. Breakup and breakdown of bent kerosene jets in gas turbine conditions[J]. Proceedings of the Combustion Institute, 2007, 31(2): 2231-2238.

[8]Bellofiore A. The penetration characteristics of normally injected kerosene liquid jet in high weber number flow[C]. 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2007, 16(4): 71-82.

[9]Chen T, Smith C, Schommer D, et al. Multi-zone behavior of transverse liquid jet in high-speed flow[C].31st AIAA Aerospace Sciences Meeting and Exhibit, 2013, 2: 122-129.

[10]Wang Q, Mondragon U M, Brown C T, et al. Characterization of trajectory, break point, and break point dynamics of a plain liquid jet in a crossflow[J]. Atomization & Sprays, 2011, 21(3): 203-219.

[11]Amighi A, Eslamian M, Ashgriz N. Trajectory of a liquid jet in high pressure and high temperature subsonic air crossflow[J]. Proceedings of Iclass, 2009,1(3):211-218.

[12]Tambe S, Jeng S M, Mongia H, et al. Liquid jets in subsonic crossflow[J]. AIAA Journal, 2004,15(9): 56-71.

[13]Yoon H J, Hong J G, Lee C W, et al. Correlations for penetration height of single and double liquid jets in cross flow under high-temperature conditions[J]. Atomization & Sprays, 2011, 21(8): 673-686.

[14]Phillips J C, Pch M, Thomas N H. Air flow and droplet motions produced by interaction of flat-fan sprays and cross flows[J]. Atomization & Sprays, 2000, 10(1):83-104.

[15]万云霞, 黄勇, 朱英. 液体圆柱射流破碎过程的实验[J]. 航空动力学报, 2008, 23(2):208-214.Wan Y X, Huang Y, Zhu Y. Experiment on the breakup process of free round liquid jet[J]. Journal of Aerospace Power, 2008, 23(2): 208-214.

[16]Less D M, Schetz J A. Transient behavior of liquid jets injected normal to ahigh-velocitygas stream[J]. AIAA Journal, 2015, 24(24): 1979-1986.