基于PCA算法的机载LiDAR点云平面分割算法研究

叶玲洁，颜远青

(1.广州市城市规划勘测设计研究院，广东 广州 510060； 2.珠海大横琴科技发展有限公司，广东 珠海 519000)

1 引 言

在建筑物的三维重建中，屋顶面提取是其中最关键的部分[1]，后续工作都在屋顶面准确提取的基础上进行。按照屋顶面的平整度，可以将屋顶面分为平面式屋顶和曲面式屋顶，现代建筑中尤其是城市建筑物，一般都较为规则，屋顶面多为平面式，而对于曲面式屋顶，难以直接用参数定义其曲面形状，常规的做法是对其构建Delaunay三角网，以三角面片的形式来拟合曲面。本文的研究重点主要是针对平面式屋顶面，因此对曲面式的屋顶面不进行研究讨论。

在屋顶面分割算法中，目前常用的主要是RANSAC(Random Sample Consensus，随机抽样一致性)算法[2]、区域增长算法[3]、三维霍夫变换算法[4]、聚类算法等。区域增长算法首先选定一个种子区域，根据屋顶面点云与种子区域的法向量夹角、空间位置关系不断地拓展面片，该方法分割效果良好，但是算法中参数选取较为困难，同时由于法向量的计算易受噪声点影响，进而使得算法增长出错误的平面。RANSAC是一种随机参数估计算法，首先从点云中随机选取三个点，计算出平面参数，然后计算其他点与该平面的偏差，当偏差小于阈值，则该点为局内点，不断迭代找到局内点最多的平面，则为最优平面模型。RANSAC能鲁棒的估计模型参数，但是其迭代次数必须足够多才能得到准确的结果，效率低下。

在进行平面拟合时，常用的方法是最小二乘法进行平面拟合，但最小二乘法对于自变量与因变量无法区分的情况，适应性差[5]，在实际中，一般认为接近垂直于地面的屋顶面是不存在的，以Z坐标作为因变量来对屋顶面进行最小二乘拟合平面。同时，在屋顶面点云存在噪声点的情况下，对拟合结果影响很大。

本文利用PCA(Principal Component Analysis，主成分分析法)来计算点云的法向量，并以区域增长法来对平面进行分割。PCA算法可以有效减小噪声点对法向量计算的影响，改善区域增长的结果。

2 平面拟合

本文中采用PCA的方法对点云进行平面拟合。PCA是一种数学变换的方法，利用降维的思想在变换中保持变量的总方差不变，将给定的一组变量线性变换为另一组不相关的变量，并且使变换后的第一变量的方差最大，即第一主成分，其他分量的方差依次递减[6]。在本文中的变量为三维点坐标的集合，其变量为X、Y、Z三个坐标值，则经过变换后，应有三个主成分，对于一个空间平面，在平行于平面的方向上点集分布最为离散，方差最大，在垂直于平面的方向上，点集分布最为集中，方差最小，即空间平面的第三主成分为垂直于空间平面的向量。由于平面拟合最关键的为法向量的拟合，利用PCA得到点集的第三主成分，即能进一步拟合出平面方程，如图1所示。

图1 PCA变换原理

对于在坐标系XYZ下的待拟合平面点云，利用主成分分析法对其进行分析，可得到三个按照从大到小排列的特征值λ1、λ2、λ3，对应的主分量分别为V1、V2、V3，其中V1和V2组成了待拟合平面的一组基，V3与V1、V2正交，为垂直于待拟合平面的法向量。如图1，在XYZ坐标系下的点云，经过主成分分析后，三个主成分分量V1、V2、V3组成了新坐标系X′Y′Z′的三个基，V1和V2为平面X′O′Z′的一组基，V3为O′Z′方向的基，即所拟合平面的法向量。

PCA过程如下：

(1)特征中心化。即每一维的数据都减去该维的均值，变换之后每一维的均值都变成了零。特征中心化后的点集P，如式(1)，其中，xi、yi、zi为中心化后点坐标：

(1)

(2)计算三个坐标的协方差矩阵。协方差矩阵C为：

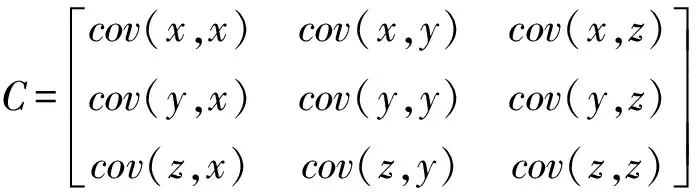
(2)

其中，cov(x，y)为x坐标和y坐标的协方差，cov(x，x)为x坐标的方差，协方差计算公式如式(3)，xi、yi为中心化后点坐标：

(3)

当协方差大于零时说明x和y是正相关关系，协方差小于零时x和y是负相关关系，协方差为零时x和y相互独立。

(3)计算协方差矩阵C的特征值和特征向量。所计算出来的特征值按照从大到小排序，分别为λ1、λ2、λ3，其所对应的特征向量分别为ξ1、ξ2、ξ3。显然，两个较大λ所对应的特征向量ξ1、ξ2为待拟合平面的一组基，而ξ3为待拟合平面的法向量，其三个分量分别为a、b、c。

若已知待拟合平面经过点p(x0，y0，z0)p(x0，y0，z0)，则拟合平面为式(4)：

a(x-x0)+b(y-y0)+c(z-z0)=0

(4)

采用主成分分析法拟合平面的方法，对于存在噪声点的情况，也能很好的拟合出结果。因为在一个平面点云中，噪声点偏离平面的距离相对于平面的范围较小，对拟合结果的影响可以忽略。

3 法向量计算

传统的平面分割算法中，对于点的法向量计算通常是采用以点为圆心，r为半径的一个邻域，取邻域内的所有点云进行最小二乘拟合，这种方法在平滑变化的曲面上，计算的结果不会有太大偏差，但是在边缘处，法向量难以确定，其结果是不准确的[7]。

本文中，首先对点的法向量进行计算。在选择点云的邻域点时，把当前表面情况考虑进去，即对于在同一个平面上，且空间上相邻近，则认为是邻域点，若不在同一个平面上，即使空间上相邻近，也不视为邻域点[8]。

图2 初始邻域点的选择

法向量计算的主要步骤如下：

(1)定义所求点的r邻域，搜索到其所有邻域点，并进行平面拟合，拟合结果为Φinit。其中，如图2，初始的邻域点为在以所求点为球心，r为半径的区域内的所有点，都认为是所求点的邻域点；

(2)计算邻域点到Φinit的距离di的中误差σ，将距离di小于两倍中误差的点权值设为1，距离di大于两倍中误差的点权值设为0。重新拟合平面Φinit；权值计算公式如(5)：

(5)

(3)多次拟合，直到所拟合的平面参数不再改变或者改变量小于阈值，此时拟合的平面为Φi。则Φi的法向量为所求点的法向量。

图3 法向量求解过程

法向量的求解过程，也就是所求点处平面的拟合过程，可以用图3表示，初始拟合的平面采用了r邻域内的所有点云进行拟合，其结果为Φinit，邻域内与Φinit的距离小于2σ的权值为1，如图中黄色点，将权值为1的点重新拟合，多次拟合，最终结果为Φi，从图3中可看出，此时所采用的用来拟合Φi的邻域点为待求点的r邻域内，且在同一个平面内的点。如图4，将以待求点为球心，r为半径的区域内，与待求点在同一个平面内的点，作为待求点的邻域点，以最终确定的邻域点来计算所求点的法向量。

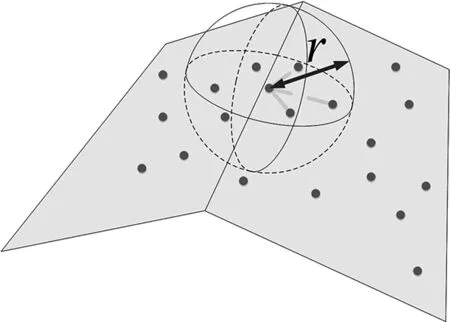
图4 最后邻域点的确定

4 平面分割

本文中平面分割的主要算法为区域增长，主要步骤如下[9]：

(1)生成分割结果列表L，种子点队列S，当前区域点列表Q；

(2)计算所有点的法向量和曲率。点pi对应的法向量、曲率分别为ni、ci；

(3)选择曲率最小且未聚类点作为种子点，将其添加到种子点队列S和当前平面点列表Q中；

④若种子点队列S为空时，当前平面提取完成，将当前平面点列表Q保存到分割结果列表L中；重置Q。

(5)最后的分割结果保存在列表L中。

在将点云数据进行平面分割后，同一个平面上的点云将被划分到同一个聚类中。此时，对其进行平面拟合，计算出平面参数。做法是采用PCA算法计算得到平面的法向量，即平面参数a、b、c，将点集内所有点求其中心，以其中心作为平面上点，计算出平面参数d。

5 实验与分析

图5 人字形屋顶面的区域增长算法分割结果

图6 锥形屋顶面的区域增长算法分割结果

图7 L形屋顶面的区域增长算法分割结果

图5、图6、图7，为三组不同数据，采用传统的区域增长对数据进行平面分割的结果，其中，angle为角度阈值，可以看出，在平面上无噪声或者噪声较少的情况下，区域增长算法提取出来的平面内部点较为连续，不会出现空洞，但在边缘处的点云无法很好地分割开。这是因为边缘处的点云法向量计算困难，无法得到其正确的法向量，因此边缘处的点云分割较为零碎，而本文中设定，当点数少于阈值时，不判别为一个平面，即一个平面上，必须有足够多的点，才能被识别出。本文设置阈值为20个点。同时，区域增长的参数不容易设置，对于不同形状的点云需要不同的参数，使得建筑物平面点云自动化分割难以实现，制约了建筑物自动化三维重建的可能。

图8 锥形屋顶面的RANSAC算法分割结果

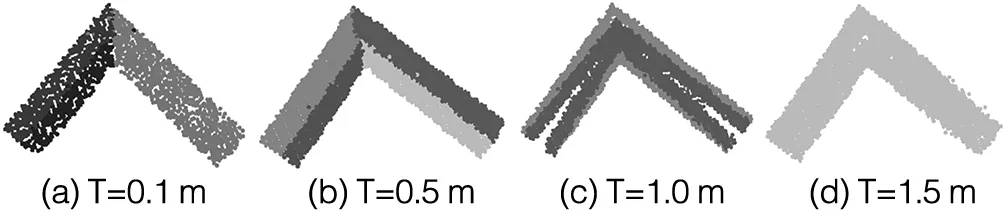
图9 L形屋顶面的RANSAC算法分割结果

图8、图9，为两组数据，采用了RANSAC算法对数据进行平面分割的结果，其中，T为阈值。可以看出，RANSAC在参数合适的时候能够较好地分割出平面。但是，RANSAC提取出的每个平面并不是等价的，第一个被提取出的平面总是会拥有更多的点，这一点在图8的T=1.0 m时表现比较明显。此外，参数不合适时，出现各种错误情况，如T=0.1 m时，平面中出现很多空洞，这是由于机载LiDAR扫描的点云在高程方向有一定的波动，但被RANSAC错误地滤掉；在第一组T=1.5 m和第二组T=1.0 m时，则出现全局最优，RANSAC只把全局内，分配到当前平面点数最多的判别为平面。

图10本文算法结果与影像对比

图10为本文算法分割结果与实际影像对比，可以看出分割的结果较为准确，在平面相交的边缘处也没有因为点云法向的不确定性而导致的错误分割或者边缘缺失的情况。

而对于图11类型的穹顶建筑，本文算法无法适应。

图11 穹顶屋顶建筑

6 结 语

本文简单介绍了常用的平面分割算法，包括三维霍夫变换、RANSAC算法和区域增长算法。三维霍夫变换需要将点云变换到属性空间，计算量较大，一般较少使用；RANSAC算法需多次迭代，效率低下，在参数不合适的时候，也容易出现全局最优而导致分割错误，此外，若第一个提取的平面拥有更多的点也导致后续提取的平面质量不断下降；区域增长算法对边缘处的法向量计算比较困难，随之出现的是边缘处的点云无法很好地分割到平面上。

本文采用PCA算法拟合局部平面的方法，并根据点到平面的距离设置权值，迭代多次后得到最准确的平面及其所对应的法向量，由于所选择的邻域一般较小，所迭代次数相对于RANSAC算法大大减少。但在屋顶面点云数量较少的情况下，噪声点对屋顶面法向量计算影响变大，容易导致法向量计算出错，从而使得分割结果错误。计算出法向量后，再以区域增长算法来对点云数据进行分割，经过实验，其结果准确，分割效果良好。根据本文算法进行点云平面分割，其结果可应用于建筑物的建模、点云分类等。本文算法主要针对平面点云的分割，对于平顶、坡顶甚至多平面复合型建筑物屋顶点云分割效果较好，但对于穹顶、曲面建筑物屋顶点云无法适用，笔者将继续深入研究并加以改进。

[1] 胡伟，卢小平，李珵等. 基于改进RANSAC算法的屋顶激光点云面片分割方法[J]. 测绘通报，2012(11)：31～34.

[2] 李娜，马一薇，杨洋等. 利用RANSAC算法对建筑物立面进行点云分割[J]. 测绘科学，2011，36(5)：144～145.

[3] 李宝顺，岑红燕，包亚萍等. 基于平面提取的点云数据分割算法[J]. 计算机应用与软件，2014，31(7)：145～148.

[4] 黄先锋. 利用机载LIDAR数据重建3D建筑物模型的关键技术研究[D]. 武汉：武汉大学，2006.

[5] 浮丹丹，周绍光，徐洋等. 基于主成分分析的点云平面拟合技术研究[J]. 测绘工程，2014，23(4)：20～23.

[6] 王松，夏绍玮. 一种鲁棒主成分分析(PCA)算法[J]. 系统工程理论与实践，1998(1)：10～14.

[7] 杨斌. 机载LiDAR点元数据建筑物半自动提取方法研究[D]. 阜新：辽宁工程技术大学，2012.

[8] Kim C，Habib A，Pyeon M，et al. Segmentation of Planar Surfaces from Laser Scanning Data Using the Magnitude of Normal Position Vector for Adaptive Neighborhoods[J]. Sensors，2016，16(2)：140.

[9] 杨洋，张永生，张皓等. 基于LiDAR数据的建筑物自动化重建[J]. 测绘科学技术学报，2010，27(2)：123～126.

[10] 姜如波. 基于三维激光扫描技术的建筑物模型重建[J]. 城市勘测，2013，3：113～116.