骨料形状及含量对碱硅反应引起的膨胀的影响

贾红刚

(许昌学院 数学与统计学院,河南 许昌461000)

碱硅反应是指混凝土骨料中的硅酸与碱发生的有害化学反应，其反应产物为硅胶体，硅胶体吸水后可导致混凝土集料体积增大，从而在混凝土内部产生很大的应力，引起混凝土内部损伤开裂,导致混凝土强度、刚度降低.碱硅反应主要的影响参数有碱含量、骨料活性、配合比、相对湿度、骨料尺寸分布、骨料结构、外力、温度等.

有关碱硅反应的参数化研究很多.Leger等[1]应用有限元数值方法研究了温度、湿度、骨料活性对碱硅反应导致的膨胀以及由膨胀引起的机械性能属性的影响,表明碱硅反应对混凝土属性有比较大的影响.Ramyar等[2]探讨了骨料尺寸和角性对碱硅反应导致的膨胀的影响,得出了压碎活性骨料对膨胀的影响比未压碎的明显,中间尺寸的骨料角形对膨胀影响明显,而其他尺寸的角性影响可以忽略.应力对碱硅反应导致的膨胀的影响也有报道[3-6],这些研究表明，应力对碱硅反应导致的各向异性膨胀可以被精确量化,应力可以降低或升高碱硅反应导致的膨胀.应力因素可以与其他因素比如碱含量耦合起来影响膨胀，但是大多仅限于单一应力因素的影响，很少有文献综合考虑骨料含量和形状研究其对碱硅反应导致的膨胀的影响.Dunant[5]研究了圆形、椭圆形骨料形状及试样形状对碱硅反应引起的膨胀的影响,但没有分析更一般的角性骨料如三角形、矩形骨料,结果表明骨料及试样形状对碱硅反应引起的膨胀曲线的诱导期形状和膨胀有重要影响.杜成斌、孙立国[7]提出了二维、三维任意形状混凝土骨料的模拟方法，得出了任意多面体骨料混凝土试件的极限承载力要大于相应圆球骨料试件的极限承载力、任意多面体骨料试件所对应的位移相对较大的结论,但是没有讨论骨料形状对碱硅反应引起的膨胀的影响.李运成等[8]研究了随机凸多面体骨料模型生成及细观有限元剖分,也是仅限于几何模型生成.Giorla[9]分析了不同形状的骨料对混凝土蠕变的影响,表明三角形骨料使得材料变得更硬,而椭圆形骨料有最大的蠕变(约为0.8)各向异性，圆形骨料几乎没有各向异性,但他没有分析不同形状的骨料对混凝土碱硅反应引起的各向异性膨胀的影响.Gao[10]讨论了耦合的试样尺寸和骨料尺寸因素对混凝土碱硅反应引起的膨胀的影响,研究表明骨料活性硅含量影响尺度效应,提出的微观模型能够量化这种尺度效应.李崇智等[11]讨论了不同岩性石粉对混凝土性能的影响.

1 扩展有限元简介

图1 圆形骨料(夹杂)富集

扩展有限元法是由Belytschko和Black[12]于1999年首次提出的一种基于单元分解法的新型有限元方法.扩展有限元的优点在于:在模拟裂纹或界面演化的过程中,不需要重新划分网格,不连续边界不需要与有限元边界一致.特别适用于模拟混凝土碱硅反应引起的膨胀,因为混凝土碱硅反应过程中,由于涉及复杂的几何界面演化,骨料和砂浆界面的模拟以及反应产物凝胶的膨胀引起骨料与凝胶边界的复杂变化,使得这些问题只有靠扩展有限元才能高效率地去模拟.本文中扩展有限元主要用于去富集骨料与凝胶边界.对于圆形骨料(夹杂)富集(图1),Moes[13]提出了一种绝对值富集函数,该函数可以写为:

(1)

其中:I表示有限元节点，x是坐标，NI是节点形函数，ζI是夹杂界面水平集函数节点值.

对于一般形状的骨料夹杂富集,使用如下的帽子型函数:

(2)

其中：Γinclusion表示骨料边界,proj是映射算子,x是坐标.

2 ASR膨胀模型

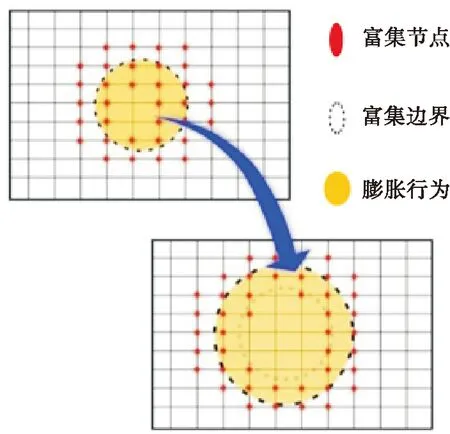
图2 XFEM富集更新

本文采用Dunant[5]所提出的ASR膨胀模型，该模型属于局部ASR反应膨胀微观结构模型.混凝土微观结构由随机堆积方法生成，骨料尺寸分布来自于对应实验中所采取的尺寸分布，最大最小骨料尺寸比为50，最小骨料尺寸为200 μm，该模型认为ASR生成的产物凝胶团随机分布在骨料里,而不是在骨料界面或其它地方,反应活性区定位在骨料中，由于活性区大小远远小于骨料，它们随着反应的进行不断扩展，因此这里用XFEM软不连续类型的富集函数来显式模拟凝胶团及其扩展，如图2所示，使用该模型可以准确地在每一个模拟步表示几何演化，凝胶假定为线弹性，人为地施加给它应变变形，并且由于凝胶受到周围的约束力，因此当反应进行到一定程度时，就会在骨料中出现损伤，当外界环境不变时,ASR生成的产物凝胶量由骨料里生成的凝胶量及凝胶所在位置决定，随ASR反应程度增大而增大.并假定混凝土是三相复合材料,由圆形或椭圆骨料,凝胶及砂浆组成,在这里，把骨料形状推广至包括圆形、椭圆形、三角形、矩形等等,不同形状的骨料总面积保持不变,为体现混凝土材料属性的非均匀随机分布,在混凝土中，骨料及灰浆矿物质属性是随其所在空间位置变化的，其力学性质也会在局部变化，因此，在骨料或灰浆单元，这种变化的力学属性的影响用Weibull随机分布律来模拟，这种局部力学属性p遵循以下的统计分布律：

p=pprescribed·(1-η)+pprescribed·η·ω.

(3)

其中：ω是随机韦伯分布变量，η为随机属性份数，η=0.2,这里的η设置是为了使模拟的数值结果与实验结果相符.

为简单起见,用二维片式微观细观结构取代实际的3D结构(图3),采用和实验试样尺寸一样的数值试样(0.07×0.07混凝土棱镜),以方便对比实验结果.

在数值实验中,混凝土颗粒尺寸分布份数采用Bolomey参考曲线提出的方法，为方便同Dunant的实验结果做对比,在所有的数值算例中,所有的混凝土配合比和颗粒尺寸分布和Dunant类似.骨料、凝胶以及砂浆均为线弹性材料,其杨氏模量分别为59 GPa、22 GPa和12 GPa,泊松比均为0.3,试样尺寸为7 cm×7 cm,所有的骨料方位与混凝土浇注方向可以成任意角度,最大骨料直径取8 mm或16 mm,它们随机分布在数值试样中,相互之间不相交,相邻骨料间的最小距离取为0.000 01 m.

图3 二维混凝土微观结构

3 数值结果及分析

算例一:耦合的骨料形状和骨料含量对碱硅反应导致的混凝土膨胀的影响.

在这个例子中,模拟了混凝土在零应力条件下的ASR膨胀,数值试样为一矩形的2D片式结构,骨料形状假定为圆形、矩形(尺寸比为0.6)、三角形(尺寸比为0.6或1)和椭圆形(尺寸比为0.6)，骨料填充率(用fill表示,骨料总面积与试样面积之比)为34%、50%、60%、62.5%.最大骨料直径取8 cm,试样尺寸为7 cm×7 cm.

图4给出了圆形、三角形和矩形骨料含量为62.5%时平行于浇注方向的ASR膨胀随时间变化的关系图,与Dunant的ASR膨胀与时间的变化趋势实验结果相符.图5给出了圆形、三角形和矩形骨料含量为34%时平行于浇注方向的ASR膨胀随时间变化的关系图.图6给出了椭圆形、矩形和三角形骨料形状和骨料含量ASR膨胀随反应程度变化的趋势，与Dunant的ASR膨胀与时间的变化趋势实验结果相符，从Dunant的ASR膨胀反应程度的变化趋势实验结果可以看出，圆形骨料膨胀是各向同性的，椭圆形骨料的膨胀曲线最接近试验结果.事实上，ASR导致的膨胀关于浇筑方向是各向异性的，这种各向异性的大小取决于骨料类型(比如形状)和试样形状，其中骨料形状通常被用来分析混凝土膨胀的各向异性.图7显示了矩形、三角形和圆形骨料混凝土Von Mises应力分布.

图4 骨料形状和骨料含量(fill=62.5%)对ASR膨胀的影响(均为平行于浇注方向的膨胀)

图5 骨料形状和骨料含量(fill=34%)对ASR膨胀的影响(均为平行于浇注方向的膨胀)

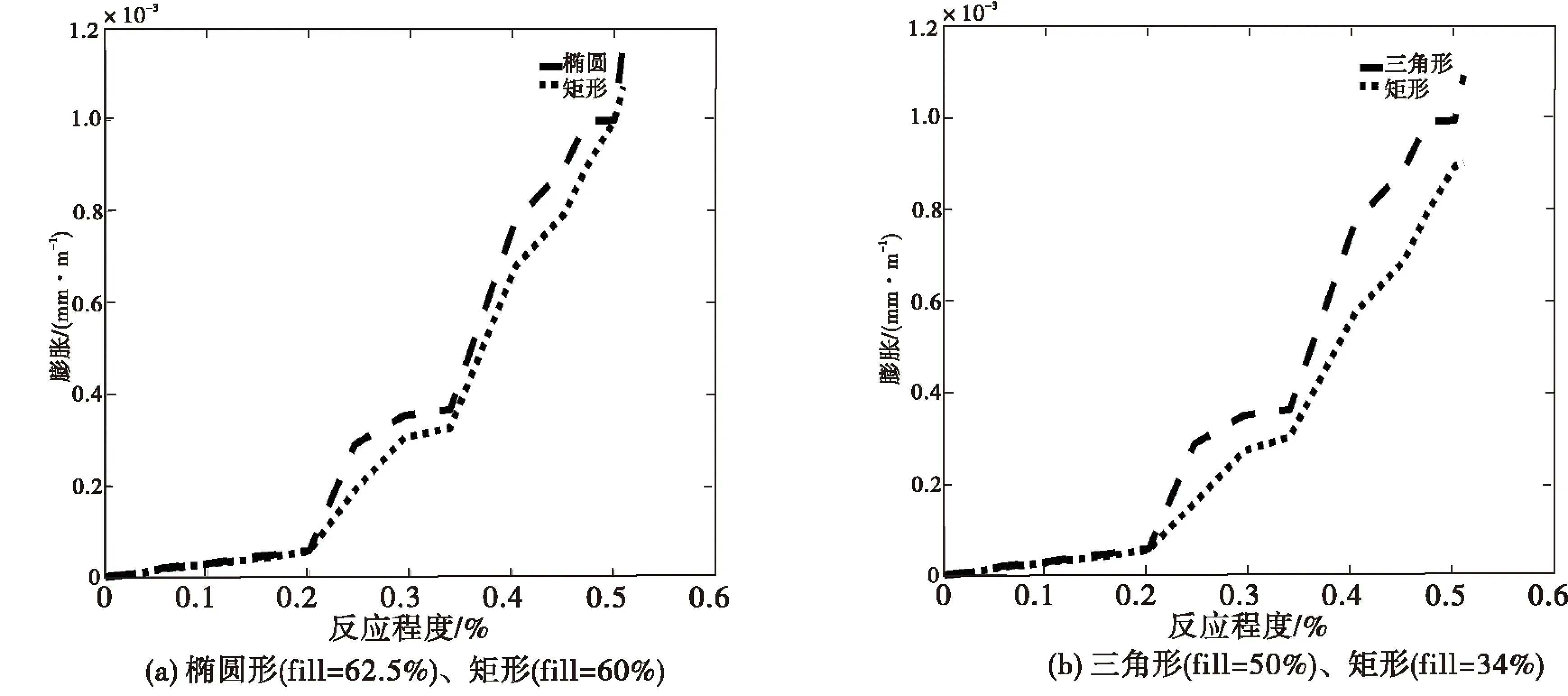
图6 骨料形状和骨料含量对ASR膨胀的影响(均为平行于浇注方向的膨胀)

图7 Von Mises混凝土应力分布(fill=34%)

从图4-图7可以看出,当骨料含量相同时，三角形骨料膨胀量最小，圆形骨料膨胀量最大，椭圆形及矩形骨料膨胀量在三角形和圆形之间.这是由于三角形骨料角性最大，应力分布有奇异性存在，奇异应力场的处理方法是在奇异点附近单元采用四分之一奇异单元，因而其刚度表现的更硬些，因而膨胀量最小,而圆形骨料最光滑，没有角性，其应力分布更光滑，其刚度表现的更小些，因而膨胀量最大.而当骨料形状相同时，随着骨料含量的升高，ASR膨胀量增大，这是由于骨料含量大时，混凝土中可获得的活性骨料面积更大，因而反应程度更高，导致膨胀量更大些.

4 结论

本研究克服了参数研究中常常忽略的耦合的骨料形状和骨料含量因素对混凝土碱硅反应引起的膨胀及应力分布的影响,研究表明:

(1)当骨料含量相同时，圆形骨料碱硅反应引起的膨胀最大,三角形膨胀最小，其他形状如椭圆形、矩形在两者之间.

(2)三角形骨料表现得刚度更硬,圆形最软.

(3)骨料形状对混凝土碱硅反应引起的应力分布有重要影响，有角性骨料产生奇异应力场，奇异应力场的处理方法是在奇异点附近单元采用四分之一奇异单元，而圆形骨料应力场更光滑，三角形骨料产生应力集中.

(4)骨料形状对混凝土碱硅反应引起的膨胀曲线的诱导期及形状有不可忽略的影响.

[1] Leger P, Cote P, Tinawi R.Finite element analysis of concrete swelling due to alkali-aggregate reaction in dams[J]. Computers & Structures, 1996, 60(4): 601-611.

[2] Ramyar K, Topal A, Andic O.Effects of aggregate size and angularity on alkali-silica reaction[J].Cement and Concrete Research, 2005, 35(11): 2 165-2 169.

[3] Berra M, Faggiani G, Mangialardi T, et al. Influence of stress restraint on the expansive behaviour of concrete affected by alkali silica reaction[J]. Cement and Concrete Research, 2010, 40(9): 1 403-1 409.

[4] Multon S, Toutlemonde F. Effect of applied stresses on alkali-silica reaction induced expansions[J]. Cement and Concrete Research, 2006, 36(5): 912-920.

[5] Dunant C. Experimental and modelling study of the alkali-silica reaction in concrete[D]. Lausanne: Ecole Polytechnique Fédérale de Lausanne, 2009.

[6] Mohsen B H. Mechanical Effects of Alkali Silica Reaction in concrete studied by SEM-image analysis[D]. Lausanne: Ecole Polytechnique Fédérale de Lausanne, 2006.

[7] 杜成斌,孙立国.任意形状混凝土骨料的数值模拟及其应用[J].水利学报,2006,37(6):662-667.

[8] 李运成,马怀发,陈厚群,等.混凝土随机凸多面体骨料模型生成及细观有限元剖分[J].水利学报,2006,37(5):588-592.

[9] Giorla A B. Modelling of Alkali-Silica Reaction under Multi-Axial Load[D]. Lausanne: Ecole Polytechnique Fédérale de Lausanne, 2013.

[10] Gao X X, Multon S, Cyr M, et al. Alkali-silica reaction (ASR) expasion: Pessimum effect versus scale effect[J]. Cement and Concrete research, 2013(44): 25-33.

[11] 李崇智,张方财,刘雷霆,等.不同岩性石粉对混凝土性能的影响研究[J].混凝土,2015(12):56-59.

[12] Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International journal for numerical methods in engineering, 1999, 45(5): 601-620.

[13] Moes N, Cloirec M, Cartraud P, et al. A computational approach to handle complex microstructure geometries[J]. Computer methods in applied mechanics and engineering, 2003, 192(28-30): 3 163-3 177.