从电磁学发展过程看麦克斯韦方程组的对称性

邓卫鹏

(阳泉师范高等专科学校 基础部，山西 阳泉 045000)

麦克斯韦方程组的创建流程及未来的开发态势，均和有关物理理论思维与物理方程形式的对称特性紧密相关，这个流程兼有唯象和抽象的特征，这两种特征现象彼此交替产生.奥斯特于公元1820年发现电流周围能够产生磁场.根据对称性的思维方式，磁场亦可形成电流.该理论的提出实际上具有唯象性，法拉第最终通过实验证实了该推断.按照法拉第电磁感应定律：变化的磁场方能够让导体形成电流.大量实验也证明了静态的磁场不能使导体中形成电流.麦克斯韦认为，变化的磁场之所以能够使导体中形成电流，是因为变化的磁场可以形成涡旋型电场，利用对称性这种抽象思维模式，大胆推测变换的电场亦可形成磁场即位移电流假说.麦克斯韦方程组的积分形式为

(1)

(2)

其中,

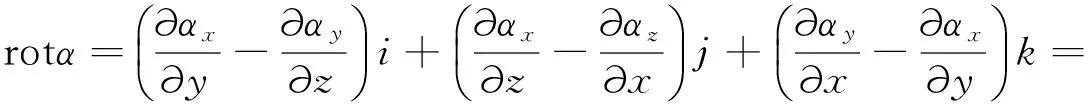
(3)

关于麦克斯韦方程组的微分表达式，我们可以通过使用高斯公式与斯托克斯公式二者结合获得公式(4)[1，2].

(4)

而麦克斯韦方程组的边值表达式为[3]

(5)

通过这些公式发现，关于麦克斯韦方程组的表述形式具有对称性，被誉为“美学上真正完美的对称形式”[4-6].然而应当注意，麦克斯韦方程组并没有绝对的对称性，由于电场内具有自由电荷，但是磁场内并没有自由磁荷(磁单极子).如果存在磁单极子，则麦克斯韦方程组才能真正变得高度对称.很多物理学家在此类对称性理论的引导下，坚决认为麦克斯韦方程组的最终模式应当具有高度的对称特性，尽管目前并未发现磁单极子，然而这并不能说明它一定不存在，何况按照狄拉克的相关理论，应当具有磁单极子，因此，物理学家对于磁单极子的探寻始终在进行.不过同样也有人认为物理领域讲的对称特性是相对的，不对称才是绝对的.

文章依次从静态与时变这两种类型的电磁场着手分析关于麦克斯韦方程组具有的对称性，进而深化对于电磁基本理论的认识.

1 静态电磁场

静态电磁场是电磁场的一类特殊形式，其场源不随时间而变化，所以其产生的场同样不随时间而发生改变，在这种条件下，电场与磁场各自独立出现.

1.1 静电场

静电场是指静止的且电荷量保持恒定的电荷激发的不随时间变化的一类静态场.静电场中并列存在的两个核心定理分别是静电场的高斯定理与环路定理.

静电场的高斯定理[1]在真空环境下，静电场内任意一个闭合曲面中的电通量其实就是曲面中电荷的代数和除以ε0，也就是(6)式，其中，q表示闭合曲面S所包围起来的自由电荷.对于有介质的情形，我们引入一个辅助性的矢量电位移矢量D，见(7)式(P为极化强度，χ为介质的极化率，ε(见(8)式)为绝对介电常数)，可以得到(9)式，化简即可得(10)式，把(7)式代入(10)式，可以得出(11)式，此式称为有介质存在的高斯定理.由(11)式，按照高斯公式，能够获得静电场的散度表达式(12)式.该式子表明，静电场具有发散特性，电荷所处的地方就是静电场的源头.

(6)

D=ε0E库+P=ε0(1+x)E库=εE库,

(7)

其中，

ε=ε0(1+x).

(8)

(9)

(10)

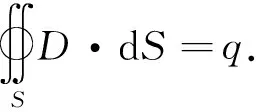
(11)

▽·D=ρe.

(12)

静电场的环路定理[1]静电场强沿着任意一条闭合曲线的环路积分等于零，即(13)式

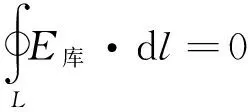
(13)

1.2 恒定磁场(恒定电流产生的磁场)

磁场的“高斯定理”[1]在稳恒电流磁场中，通过任何闭合曲面S的磁通量恒定为零，也就是(14)式.该式表明，电流磁场属于无散场；而静电场具有发散性，电荷所处的地方则是静电场的源头.磁感应线和电场线也有区别：电场线始于正电荷终于负电荷，或始于正电荷终于无穷远，或始于无穷远终于负电荷；而磁感应线具有持续性，它可以处于闭合状态，也可以从无限远的位置开始，于无限远的位置结束.由(14)式，按照高斯公式，能够获得关于恒定磁场的散度表达式(15)式.此式说明，稳恒磁场实际上属于一个没有通量源的矢量场.

(14)

▽·B=0.

(15)

安培环路定理[1]在真空环境下，磁感应强度B沿着任意闭合环路L所产生的线积分(环流)，等于穿越这一环路的全部电流强度的代数和I的μ0倍，见(16)式.如果有磁介质出现，安培环路定理表达式即为(17)式(其中，I0、I′分别表示穿越L的传导电流和磁化电流的强度).引入物理量磁化强度M进一步化简(17)式可以得出(18)式，从便利的角度考虑，再引进一个具有辅助性特征的矢量磁场强度H，见(19)，式中g是一个反映磁介质磁特性的量，(19)式变形可得(20)式，因此(18)式可变为(21)式，这个式子就是在具有磁介质的情形下的安培环路定理.

(16)

(17)

(18)

(19)

B=μH.

(20)

(21)

2 时变电磁场(两大假设)

在这种时变型的电磁场内，变化的磁场会形成电场，变化的电场也会形成磁场，时变型的电磁场内着重陈述了电场和磁场跟随时间从而发生变化的相互联系.

麦克斯韦假设一：空间变化的磁场会形成具有时变特征的涡旋电场(感生电场)，即著名的法拉第电磁感应定律[1].

(22)

其中，E=E库+E感，q为闭合曲面S所包围的自由电荷.

由(13)和(22)，根据斯托克斯公式，可以得到库仑电场和感生电场的旋度表达式，即(23)式.由(6)和(22)可知：E库为发散场，E库线从正电荷开始到负电荷终止；而E感是无散场，E感线是无头无尾的连续曲线.E库是位场(无旋场)，可以引入电位概念；而E感为涡旋场(非位场)，无法引进电位概念.由于感生电场为涡旋场，因此在变化的磁场内，只有处于静止状态下的闭合线圈中才有形成感生电动势的可能.

麦克斯韦假设二：麦克斯韦位移电流假说——变化着的电场激发涡旋磁场.

在研究分析可变电流磁场时，通过使用安培环路定理，发现和电荷守恒定律具有一定的冲突.麦克斯韦基于此情形下大胆地提出了著名的全电流定律与涡旋电流假说[1].

麦克斯韦假设在一般(例如非稳恒)情形下高斯定理仍旧成立，即(11)式.(11)式两边对时间t实施求导即(24)式，通过移项化简就得到(25)式，引入位移电流密度jd即(26).麦克斯韦假设在非稳恒条件下，磁感应强度H沿着任意闭合曲线的线积分(环流)满足(27)式.由(27)式，按照斯托克斯公式，能够获得关于时变磁场的旋度表达式(28).

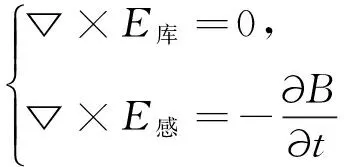
(23)

(24)

(25)

其中，

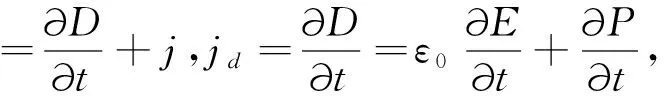
(26)

(27)

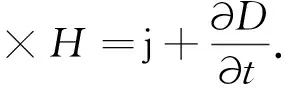
(28)

位移电流、传导电流是两个不同的物理概念，共同点在于它们能够依据同样的规律引发磁场，其他方面则完全不一样.在真空环境下，位移电流仅仅等同于电场强度的矢量改变，并未出现电荷或任何其它形式的物理运动；另外，位移电流并不生成焦耳热，对于真空环境而则言更加显著.

3 结语

关于位移电流的假说，说明麦克斯韦在处理电磁场理论问题的时候选用了动力学方法，实验也证实了这一点.麦克斯韦方程组适合于静态和时变的电磁场中.磁场和电场在变化的空间中充相互交织[5]，形成电磁场.麦克斯韦创建的电磁场理论是是电磁思想的革命性转变.我们经过对有关麦克斯韦方程组的内容、创建流程、物理意义，以及不同电磁条件下实施的探讨分析，深化了对于麦氏方程组的认识.

[1] 梁灿彬，秦光戎，梁竹健.电磁学[M].北京：高等教育出版社，1980.

[2] 郭硕鸿.电动力学[M].北京：高等教育出版社，1997.

[3] 冯慈璋.电磁场[M].北京：人民教育出版社，1979.

[4] 程守沫，江之永.普通物理学[M].6版.北京：高等教育出版社，1982.

[5] 陈康生.电磁场与电磁波[M].北京：高等教育出版社，2007.

[6] 邹祖莉.用科学发展观探究《电磁学》中的对称性[C].贵州省科学技术优秀学术论文集，2004：426-428.