基于线性锥规划的风电最优潮流研究*

薛琢成，杨冰芳(上海理工大学 电气工程系，上海 200093)

0 引 言

近年来，我国风电装机容量连续4年位居世界第一[1-2]。因风力资源的间歇性和波动性，对于风力发电，风速的不确定性会对电网潮流带来较大冲击，所以探讨风电并网对电网最优潮流的影响具有重要意义。

目前，最优潮流优化方法大致分为经典算法和智能算法两大类。经典算法主要包括：牛顿法和简化梯度法[3-4]。随着人工智能和机器学习的兴起和不断改进，智能算法逐步应用到电力系统中，智能算法主要包括：群类优化算法以及遗传算法等[5-6]。文献[7]在风电场最优潮流模型中，以电压波动和网损最小为目标，利用改进粒子群算法求解，大幅降低了网损和电压越界的可能性；文献[8]通过简化异步风电机等效稳态模型，利用混沌优化方法计算风电场最优潮流，得到了更为精确的结果；文献[9]指出传统优化算法存在局限性，在数学上不能严格证明求解结果一定是原问题的最优解，求解过程容易陷入局部最优。随着凸优化理论的发展，其具有全局最优的特性给研究带来了新方向，其关键之处是通过松弛方法处理，将最优潮流的非线性规划问题转换为凸优化问题。最为常用的松弛方法包括半定规划(SDP)和二阶锥规划[10-13]。

本研究考虑风电出力随机特性建立风电最优潮流模型，在潮流计算中将风电场出力从PQ节点注入[14]，其有功功率即为机械功率，与风速变化有直接关系，利用Weibull分布生成随机风速，计算风电场的有功和无功功率[15]。

1 风电场数学模型

1.1 风机稳态数学模型

简化后的等值电路如图1所示。

图1 异步电机简化等值电路x1—定子电抗；r2/s—转子折算后的电阻，s<0；x2—转子折算后的电抗；xm—励磁阻抗；U—异步电机端电压；I—异步电机电流值

则风机输入电力网络的有功功率Pe为：

(1)

其中，xk=x1+x2。

由此可得，发电机滑差为：

(2)

其吸收的无功功率为：

(3)

1.2 风速模型及风电场输出功率模型

大量研究表明，风电场的风速模型近似服从韦伯(Weibull)分布。设某一已知电力系统的风电场，其风速为v，则该风速的概率密度函数表达式为：

(4)

其数学期望和方差分别为：

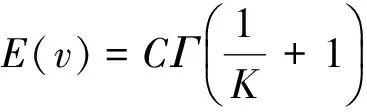
(5)

式中：C—尺度参数，其值即为该风电场的风速的期望值；K—形状参数，反映Weibull分布的偏斜度；Γ—Gamma函数。

这两个参数的精度影响风速分布的精度，其中K的近似值可由实际风电场测风所得到数据得到。

对于小规模的分布式风电场，可以认为该风电场内的所有风机受风速影响相同，因此其出力可以表示为：

(6)

(7)

式中：PW—单台风机出力；Pr—风轮输出额定功率；Cp—风轮的功率系数；A—风轮扫掠面积；ρ—空气密度；v—风速；vci—切入风速；vr—额定风速；vco—切出风速；k1和k2—风速在(vci，vr)区间内风机出力曲线参数，共同决定了风机出力的大小。

故节点i风电场的输出总功率为：

PWi=NWiPW

(8)

式中：NWi—节点i所接风电场装机的总台数。

假定每台风机以恒定功率因数运行，则节点i风机吸收无功总量为：

QWi=PWitanθi

(9)

式中：θi—节点i风电场的功率因数角。

2 风电最优潮流模型

最优潮流就是当系统的结构参数及负荷情况给定时，通过控制变量的优选，使得找到的系统运行状态能满足所有指定的约束条件，并能使系统的某一个性能指标或者目标函数达到最优时的潮流分布，即：

(10)

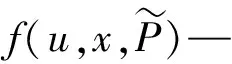
2.1 目标函数

发电成本只为常规机组燃料消耗：

(11)

式中：f—系统总发电成本；ai，bi，ci—每台发电机对应的经济参数；NG—系统发电机数；PGi—每台发电机的出力。

2.2 功率平衡约束

正常工作状态下系统的功率平衡方程为：

(12)

2.3 安全运行约束

(13)

3 二阶锥规划模型

3.1 二阶锥标准型

SOCP具备锥规划的所有特性。二阶锥规划是在一个仿射空间和有限个二阶锥笛卡尔积的交集上求一个线性函数极值的问题。其目标函数须为线性，可行域由线性等式或线性不等式约束与旋转锥或二阶锥不等式约束组成[16]，标准形式为：

ming(x)
s.t.Ax=b,x∈C

(14)

式中：g(x)—目标函数；Ax=b—线性约束，A∈Rn,x∈Rn×m,b∈Rm；C—二阶锥约束。

锥规划的基本形式有二阶锥和旋转二阶锥两种：

(15)

锥规划作为线性规划的推广，是半定规划的特例，属于凸规划的一种，在数学上能严格证明具有全局最优解，而不会陷入局部最优中。利用相关数学求解器(如CPLEX、YALMIP)求解，可以进一步提升计算效率。

3.2 二阶锥变换

目标函数中带有二次项，不满足二阶锥规划形式，故做以下变换:

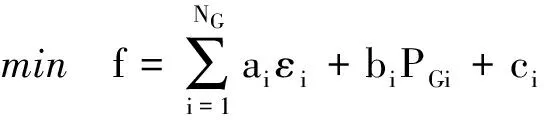
(16)

式中：εi—引入的中间哑变量[17]；E—单位矩阵，把原模型转化为二阶锥模型求解。

本研究交流潮流中的约束大多为非线性和非凸性，增大了求解难度。因此通过加入中间变量，转化为二阶锥形式，成为凸规划问题。现进行如下变换，设：

(17)

则原先潮流中功率平衡约束条件变为：

(18)

安全运行约束中非线性约束变为：

(19)

(20)

增加二阶锥表面约束：

(21)

由式(18～21)构成了系统潮流的二阶锥形式，由于式(21)含有二次项，可行域在二阶锥表面，整个模型仍为非凸规划问题。为便于求解，将式(21)松弛为：

(22)

经过SOC松弛后，可行域变为二阶锥体，成为凸规划问题。松弛原理如图2所示。

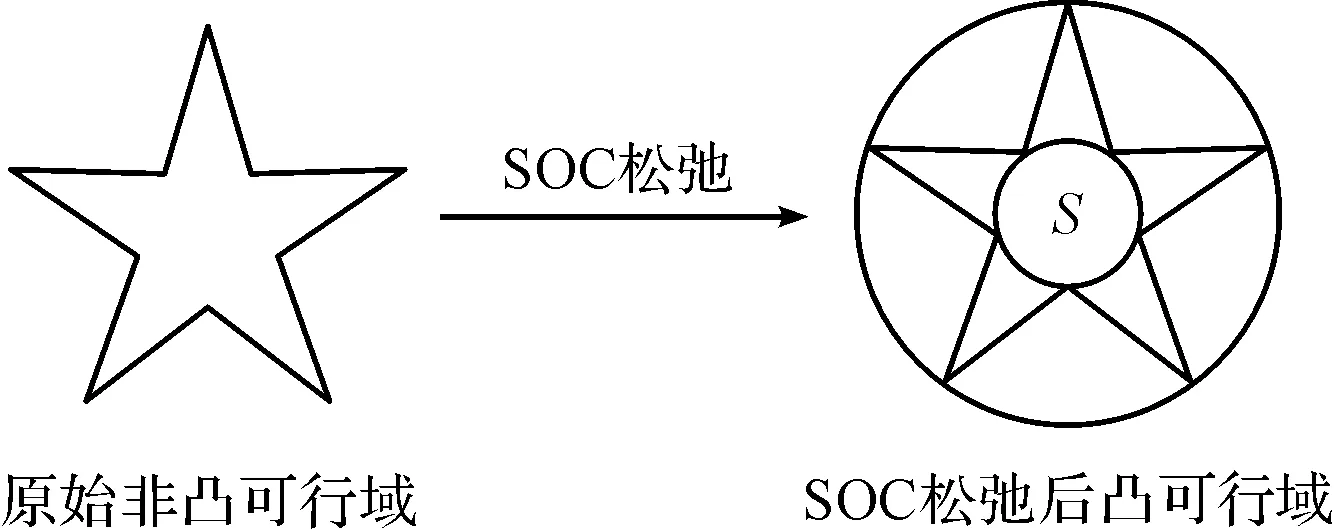
图2 二阶锥松弛原理

松弛后得到的最优解S表示原问题的下界解，若最优解在松弛前的可行域内，则说明S就为原问题的最优解，该松弛为严格松弛[18-19]。松弛后的模型可以用YALMIP[20]数学优化软件包求解。

4 实验及结果分析

本研究选择IEEE9和IEEE14节点系统来测试提出的模型与算法，并将其与混沌优化和线性规划作比较。在IEEE9节点系统中将等值风场接入3号节点，系统包含9条支路、3台发电机。设定风机功率因数120°，风电机组切入风速3 m/s，额定风速13 m/s，切出风速20 m/s。

在额定风速为13 m/s情况下系统的最优潮流分布情况如表1所示。

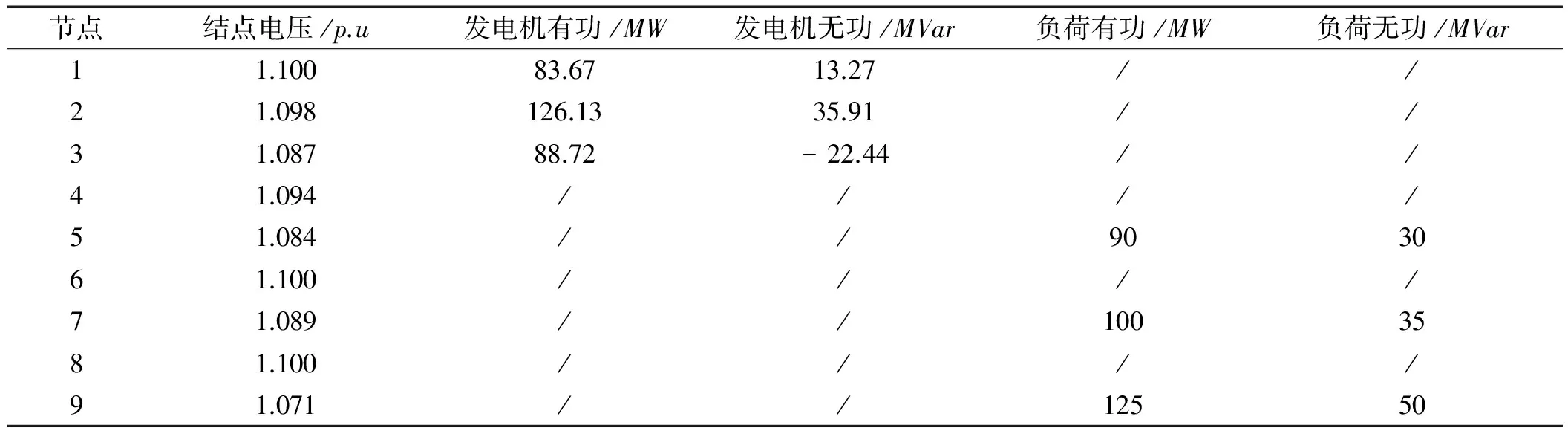
表1 采用SOCP的IEEE9节点潮流计算结果

从结果可以看出，此时节点电压趋近所设电压约束的上限，说明此时无功充足，电压稳定裕度较大，系统能承受的负荷增长空间较高，能给风电场提供更多的无功供给。

SOCP与混沌优化法和线性规划的计算结果如表2所示。

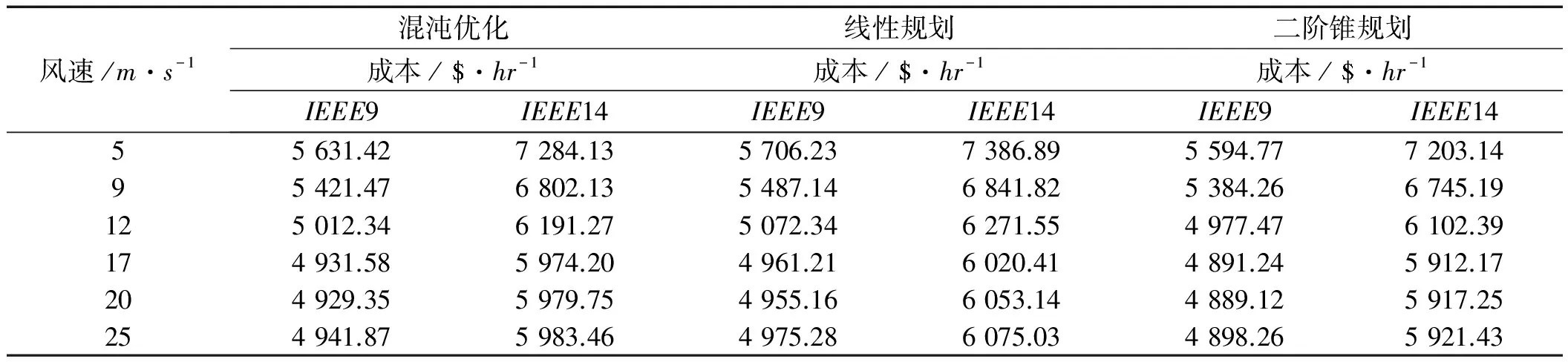
表2 优化前后发电费用对比

其中，部分数据参考文献[7]，将风电场接入14号节点。从中可以得出：(1)在不同风速条件下，随着额定风速的增大，发电成本随之减少，但超过约17 m/s后，成本不再减少，呈现出略有上升的趋势，所以风电的经济效益在某些条件下出现饱和现象；(2)混沌优化后的模型比线性规划求解的发电成本要更低，在这3种优化方法的对比中，利用二阶锥规划求解模型得出的成本最低，随着节点数的增多，效果更明显。

为验证松弛前后的有效性，在式(16)和式(22)最优解处取等号是否满足，故作出如下分析，引入公式：

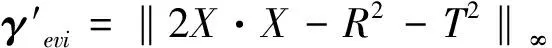
(23)

其中，元素是节点偏差量的无穷范数。其分布趋势如图3所示。

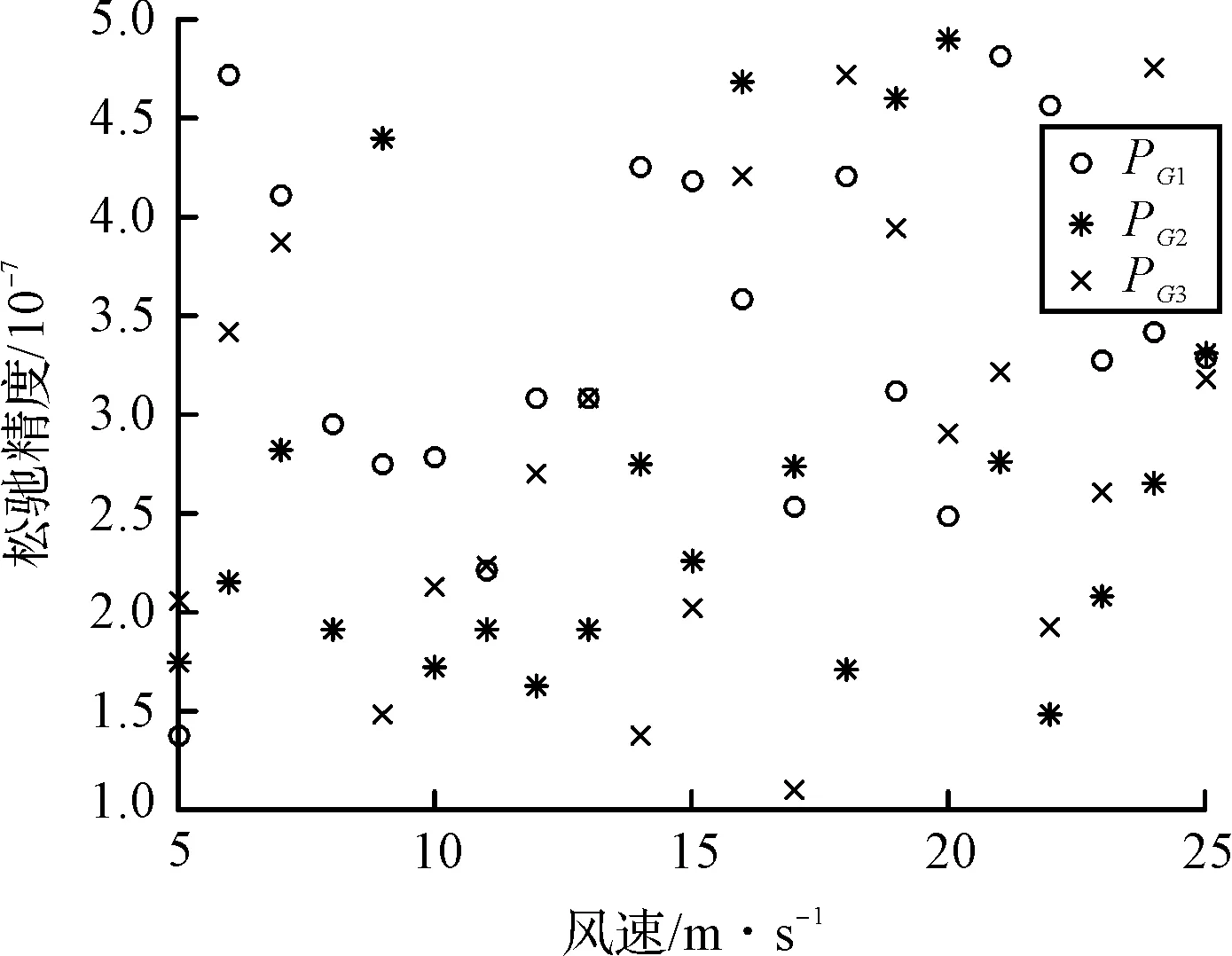
图3 发电机变量松弛偏差散点图

图3中，3种散点类型分别表示发电机1、2、3的松弛偏差量。从图中可以发现经过二阶锥松弛之后的发电机的出力以及中间变量偏差最大值都在10-7数量级，满足潮流的收敛判据，说明本文的松弛方法准确可靠。

5 结束语

在考虑风电出力不确定情况下，本研究建立了风电最优潮流模型，并在IEEE9和IEEE14节点系统中进行了仿真。研究结论如下：

(1)在最优潮流中考虑在不同风速下风电出力的随机特性，通过二阶锥规划求解，把非线性约束转换为若干线性约束，通过与线性规划和混沌优化方法的分析比较可以得出：在保证最优解的同时，降低了计算的复杂程度；

(2)在电力系统中加入风电会有更好的经济效益；随着风速的增加，系统的发电成本随之降低，但存在上限。

[1] 电力简讯.国家电网公司在京发布《国家电网公司促进新能源发展白皮书(2016)》[J].电力与能源,2016(2):171.

[2] 周姝灿，唐俊熙.风电、储能参与系统调频的协调控制策略研究[J].机电工程技术，2017，46(11)：31-35.

[3] 诸骏伟,金心明,朱正明.一种快速收敛的牛顿法最优潮流[J].东南大学学报：自然科学版,1992,22(4):1-7.

[4] 袁智强,侯志俭.优化算法与最优潮流[J].华东电力,2002,30(2):1-6.

[5] 刘前进,许慧铭,施 超.基于人工蜂群算法的多目标最优潮流问题的研究[J].电力系统保护与控制,2015，43(8):1-7.

[6] DEVARAJ D, BANU R N. An improved genetic algorithm approach for security constrained optimal power flow with corrective action[J].InternationalJournalofPower&EnergyConversion,2013,4(4):355-368.

[7] 吴杰康,程鹏飞,赵莎莎.基于协调粒子群算法的含风电场电力系统最优潮流计算[J].现代电力,2011,28(6):87-91.

[8] 张 伟,卫志农,刘玉娟.基于混沌优化的含风电场的最优潮流计算[J].中国电力,2011,44(10):25-28.

[9] 博赛克斯 D P.凸优化理论[M].北京：清华大学出版社,2015.

[10] JABR R A. Exploiting sparsity in SDP relaxations of the OPF problem[J].PowerSystemsIEEETransactionson,2012,27(2):1138-1139.

[11] 白晓清,韦 化, FUJISAWA K.求解最优潮流问题的内点半定规划法[J].中国电机工程学报,2008,28(19):56-64.

[12] KUANG X, GHADDAR B, NAOUM-SAWAYA J, et al. Alternative LP and SOCP hierarchies for ACOPF problems[J].IEEETransactionsonPowerSystems，32(4)：2828-2836.

[13] KOCUK B, DEY S S, SUN X A. Strong socp relaxations for the optimal power flow problem[D]. Atlanta: Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology,2015.

[14] 鲍海波,韦 化.考虑风电的电压稳定概率评估的随机响应面法[J].中国电机工程学报,2012,32(13):77-85.

[15] 赵俊华,文福拴,薛禹胜,等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化,2010,34(20):22-29.

[16] 李洪美,崔翰韬,万秋兰.考虑电动汽车充电策略的配网重构二阶锥规划模型[J].中国电机工程学报,2015,35(18):4674-4681.

[17] 丁 涛,柏 瑞,孙宏斌,等.基于鲁棒均值-方差优化的发电自调度算法及鲁棒代价分析[J].中国电机工程学报,2015,35(2):319-326.

[18] FARIVAR M, LOW S H. Branch flow model: relaxations and convexification (Parts I, II)[J].IEEETransactionsonPowerSystems,2013,28(3):2554-2564.

[19] YANG W, ILICÉ M D, QIAO L, et al. Convexification of bad data and topology error detection and identification problems in AC electric power systems[J].IetGenerationTransmission&Distribution,2015,9(16):2760-2767.

[20] JOHAN L. YALMIP: a toolbox for modeling and optimization in MATLAB[J].SkeletalRadiology,2011,41(3):287-92.