基于图像的NAO机器人松协调运动研究*

王宪伦，姜鹏鹏，冯现东，崔玉霞(青岛科技大学 机电工程学院，山东 青岛 266042)

0 引 言

在工作任务复杂或环境多变时，双臂机器人与单臂机器人相比具有以下技术优势[1]：适用范围广、协作能力强、可靠性高，所以双臂机器人应用领域非常广泛。如在工业领域中，完成复杂的装配作业、搬运较重的货物、维修构型复杂的工件等，在一些危险而恶劣的放射环境中代替人类完成不能现场完成的任务，如核电站维护。在服务领域，双臂机器人可以较好地模拟人类行为，如医疗看护机器人可以代替护士来看护病人，养老机器人可以解决老年人生活中的各种不便。近几年国内外双臂机器人产业迅速发展，例如，美国Rethink公司的Baxter[2]，该机器人已在美国的一些企业进行了测试，代替人完成大量作业；瑞士ABB公司的FRIDA[3-4]，该项目联合了多个世界范围内技术力量雄厚的高校和研究所，对机器人操作的安全性、精密性，机器人控制的柔顺性等方面进行了系统性研究；法国Aldebaran机器人公司的NAO机器人[5-6]，已经被全球50个国家的550间顶尖高校和实验室购买作为研究工具；北京理工大学研制的“汇童”5代机器人[7]，实现了与人的乒乓球对打。

双臂机器人技术是机器人领域中的研究热点，而协调运动更是机器人领域中关键技术之一。丁希仑等将机器人协调运动分为松协调和紧协调两种，松协调是指在同一工作空间中分别执行各自无关的作业任务，紧协调是指在同一工作空间中执行同一或多项作业任务。松协调过程中机械臂所需定位精度与实际应用中所要求的最小精度有关，如在倒水或拧松螺丝时，协作要求的精度远小于机器人本体定位精度，使用基于图像的视觉伺服对机器人各构件的加工与装配精度要求降低，受构件磨损的影响较小，故只需保证机器人构件的刚性，进而大大降低了相应制造维护成本。

本研究采用基于图像视觉伺服来实现NAO机器人双臂协调运动中的松协调任务。

1 目标识别

机械臂、工具和目标上具有一些图像特征点，但这些特征点不通用、不易控制和识别，因此一般在关键的地方设置Mark点。NAO机器人能识别NAO-Mark点，但该Mark点的识别算法要求Mark点在图像上有较大面积才能识别。而在机器人协调运动中采用的Mark点图像面积较小，较大的图像面积会极大的限制协调过程的运动空间。故本研究提出了一种形如NAO-Mark的标记并对该标记的编码解码和定位提取识别过程进行了分析与实现。设最外圆半径为R，该标记的外边采用宽度为0.2×R的环形，在环形内将一个圆分割为n等分，并涂为黑色或白色，8等分的标记称为Mark-8，如图1所示。

图1 Mark-8

1.1 Mark-8标记的编码解码

Mark-8标记的编码过程为：以任意白色与黑色的交界线开始，将一圆环逆时针等分为8份。按照逆时针顺序依次编码，若该等份为白色则置为1，反之则置为0，从左到右依次排开，再将编码按位取反。以图1为例，从水平的分界线开始按逆时针依次编码得10100100，再按位取反得01011011，换算成十进制则为91。

从编码中获得标记旋转不变的唯一编码即识别码，并将从任意编码获得唯一性识别码的过程称为解码过程。以图1定义轮换操作，将编码进行左移操作得101001000，再将最前一位放到最后一位得轮换编码01001001。可知任意8位编码共有7个轮换编码，取该编码及其7个轮换编码中最小值作为识别码。

1.2 Mark-8标记的定位提取识别

在含编码标记的图像中提取出编码域是实现进一步提取的前提，而Mark-8标记其外部分割线为圆，其投影到图像中应表现为圆或椭圆，故通过识别椭圆状轮廓即可实现编码域在图像中的分割提取。本研究采用基于Canny算子的边缘检测法，然后对检测到的边缘进行初步筛选，去除长度过小的边缘，本研究中将长度小于10的边缘视为过小，对剩下的边缘利用最小二乘法进行椭圆拟合。

对任意位置的椭圆，其一般方程为：

f(x,y)=x2+Axy+By2+Cx+Dy+E=0

(1)

设定构成轮廓的点个数为N(N>5)，则对轮廓点作为最小化目标进行求解与拟合即可得椭圆，如下式所示：

(2)

FITZGIBBON[8]用最小二乘法对式(1)在多种情形下的求解进行了详细分析。由最小二乘法所求得式(1)中参数可进一步获得拟合椭圆5个基本参数：

(3)

(4)

(5)

(6)

(7)

所得椭圆中心像坐标(xc,yc)即为目标Mark点的像坐标。评估轮廓扁圆的程度，用所得椭圆短轴b的长度比上其长轴a的长度，得到的比值即b/a作为评判值。通过设定评判阈值即可将过扁的轮廓去除。

为了便于从图像提取编码，本研究将Mark目标区域通过透视变换变换到一个方形图像中。利用拟合轮廓得椭圆中心(xc,yc)、长轴a、短轴b、转角θ，同时为截取过程中不破坏椭圆轮廓，在计算中将长短轴扩大一定倍数，按照如下算法即可求解出将椭圆包裹的旋转矩形各角点坐标：

anew=a×scalar,bnew=b×scalar,xp1=xc-sin(θ)×anew-cos(θ)×bnew,
yp1=yc+cos(θ)×anew-sin(θ)×bnew,
xp2=xc+sin(θ)×anew-cos(θ)×bnew,
yp2=yc-cos(θ)×anew-sin(θ)×bnew,
xp3=2xc-xp1,
yp3=2yc-yp1,
xp4=2xc-xp2,
yp4=2yc-yp2。

因识别标记的图像大小为100×100，旋转矩形四角点与该图像上4点分别对应，对应关系为：(xp1,yp1)↔(0,0)、(xp2,yp2)↔(100,0)、(xp3,yp3)↔(100,100)、(xp4,yp4)↔(0,100)。由上述4个对应点对即可求得相应的透视变换矩阵，应用该透视变换将目标区域映射到标记识别图像中，提取的结果如图2(a)所示。对提取图像进行直方图均衡化，并阈值化处理，得到结果如图2(b)所示。

图2 Mark-8图像的提取结果

经过透视变换后Mark标记的中心即椭圆的中心位于识别图像的中心，故标记图像中的环形部分在对数极坐标图像中将表现为一条直线，而用来编码的扇形域就会在对数极坐标图像中形成间隔的条文。本研究对二维图像进行变换得对数极坐标图像。取缩放比M=20，则得到的条纹图如图3所示。

图3 条文图像

1.3 目标坐标系的确定

在NAO机器人松协调过程中起主要作用的是两个机械臂的末端连杆，其上有手爪等执行器，为了固定工件或工具还需特定夹具。在基于图像视觉伺服过程中，并不需要正逆运动学等计算来获取两末端坐标系的确切描述，仅需在工件或工具上放置适当数量标记点，便可通过视觉系统求解得工件(或工具)坐标系。但该过程不仅对放置标记的数目有要求，且需已知各标记在工件坐标系中的三维位置。本研究提出一种解决方案：首先设计夹具来夹取工件或工具，再设计特定夹具装到机械臂的末端，使得用该夹具夹取带夹具的工件或工具时能保证工件或工具在末端连杆系中处于固定位姿，然后向工件或工具上添加适当数量Mark点标记，并用已标定的含视觉机械臂系统识别出各Mark点标记在末端坐标系中位置。同类型臂下Mark点标记位置在末端系中位置不变，即工件或工具被未视觉标定同类臂夹取时可以通过Mark点标记识别出其位姿。

2 视觉控制流程

本研究实现松协调策略的情形和方法如下：加持工件的为工件臂，加持工具的为工具臂，设工件臂上有4个标记点则在内参已知的相机下可通过PnP问题求解在相机坐标系下工件坐标系位姿[9]。设工具臂上有一标记点称为工具点，则机械臂的松协调过程变为使工具点在工件坐标系下按给定规律运动。此时工件臂位姿由规划器获得，使工件按指定轨迹运动。为使所求工具点为唯一空间点，至少需两个内参已知的相机来组成视觉系统。

控制流程图如图4所示。

(1)从各相机图像中得到所有标记点描述及其像坐标，并用标记点识别码从知识库获得该标记点的分类来判断其属于工件标记点还是工具标记点；(2)在各相机坐标系中用工件标记点坐标和知识库中该点在工件坐标系下的位置来重建工件坐标系，再由工具点在工件坐标系下运动规律计算得工具点的目标位置并用相机成像模型得到工具点的目标像坐标；(3)将工具点当前像坐标和目标像坐标的差值带入视觉伺服控制算法，求得工具臂关节角向量来控制工具臂的运动。

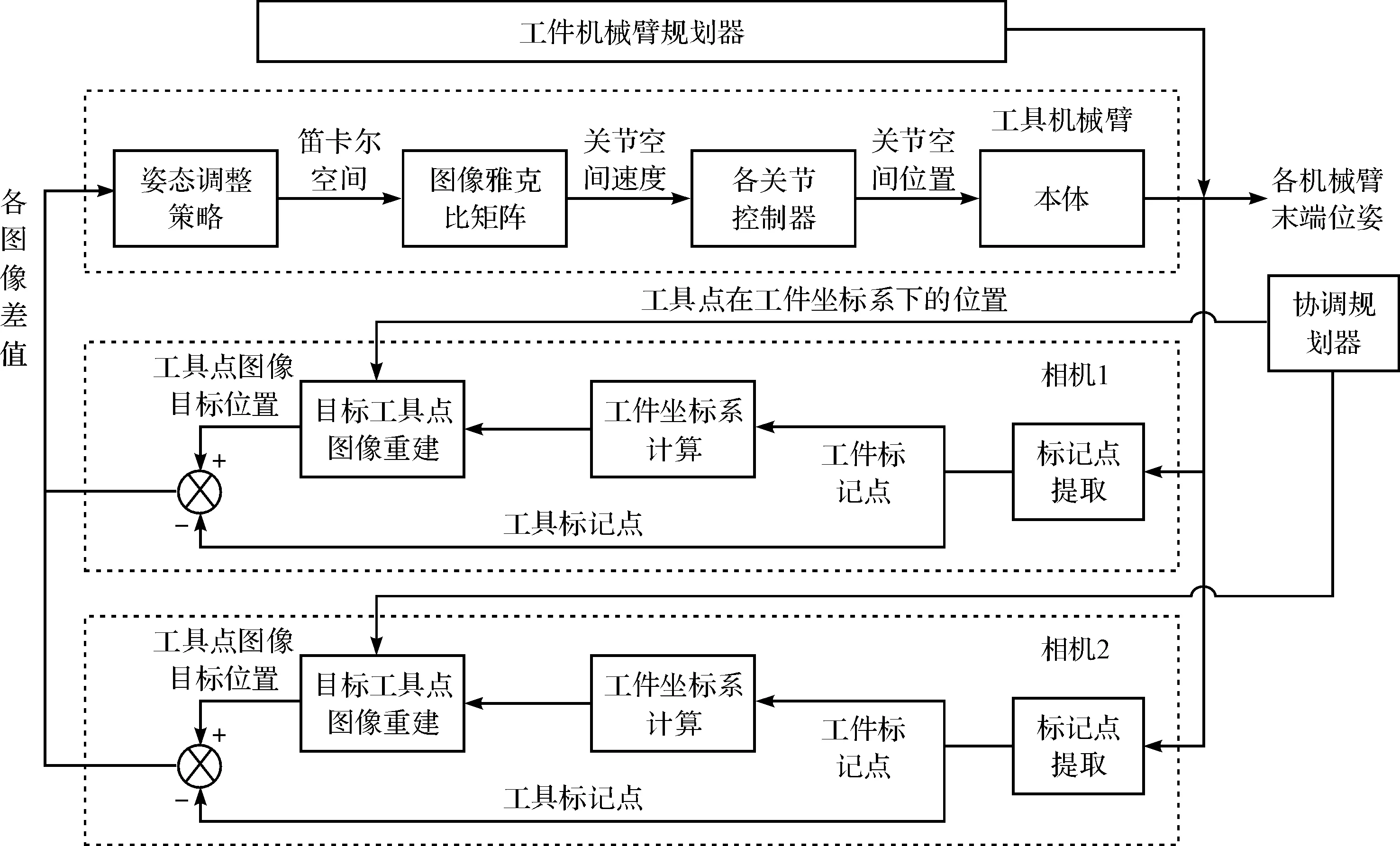
图4 松协调控制图

3 实验及结果

该实验用NAO机器人的左右两臂构成双臂机器人系统，利用NAO机器人的下摄像机和一个固定在世界坐标系下的相机来构成视觉系统。令NAO机器人的左臂为工件臂、右臂为工具臂。在工件臂末端放置四个Mark-8标记，作为工件标记。在工具臂末端放置一个Mark-8标记，作为工具点。

初始状态下其外观配置如图5所示。

图5 机器人松协调实验环境

此时机器人头部运动链的关节角向量为：[-0.006 18,-0.227 074]T；

左臂运动链的关节角向量为：

[0.495 4,-0.150 7,-1.023 2,-0.751 6,1.813 1]T；

右臂运动链的关节角向量为：

[0.638 2,0.015 3,1.060 0,0.906 6,-1.811 7]T。

两机械臂的初始状态在机器人下相机{BCam}和外部相机{CamPP}的图像如图6所示。

图6 两机械臂的初始状态

初始状态下，由Mark标记识别法可得各标记点在相机中的像坐标，如表1所示。

表1 初始状态时各标记点在各相机中的图像坐标

让NAO机器人左右臂各随机运动5次，每次运动后各机械臂的关节角如表2所示。

表2 五次随机运动的关节角

同时从机器人下相机图像所得各标记点的图像坐标如表3所示。

表3 各标记点在NAO机器人下相机中的图像坐标

求得4个工件标记点在左臂末端坐标系下的位置和工具标记点在右臂末端坐标系下的位置如表4所示。

表4 各标记点在其所属机械臂末端坐标系中的坐标

使工具臂随机运动10次，求得初始状态工具臂的图像雅克比矩阵：

由于NAO的机械臂仅有5个自由度，不能保证任意空间位姿可达，故令工件臂运动链关节角从[0.495 4,-0.150 3,-1.023 2,-0.751 6,1.813 1]T运动到[0.445 4,-0.070 3,-1.023 2,-0.851 6,1.713 1]T，工具点在工件坐标系下从[10.032 4,-86.666 1,75.174 5]T运动到[5.032 4,-76.666 1,75.174 5]T，则在两个相机下理想的运动轨迹如图7所示。

采用本研究的控制方法所得运动轨迹则如图8所示。

图7 理想运动轨迹

图8 仿真运动轨迹

从图中可以看出：该运动方案具有较高可行性，存在运动精度稍低、抖动的问题。这主要是由于仿真控制的细分数量较低，实验中所用细分数为10，即将整个协调运动过程分成了10步来求解，导致其结果的稳定性下降；其次所求初始状态下图像雅克比矩阵有一定误差，导致在起始几个运动过程中的误差相对较大。提高仿真的细分数显然能够提高运动稳定性，但计算次数会增加，这对应于控制过程中控制周期的缩短，进而对整个系统的要求都会提高。初始状态下的雅克比矩阵的精度与采集次数及识别精度有关，可以通过增加采集次数或大量学习的方法来提高。

4 结束语

本研究提出了一种Mark标记点的视觉识别及相对定位方法，在NAO机器人左臂末端附有4个Mark点，在右臂末端附有一个Mark点，用NAO机器人左臂模拟加持工件的机械臂，右臂模拟加持工具的机械臂，利用NAO的下相机和一个外部相机构成视觉系统，构成基于图像的协调运动环境。对基于图像的松协调运动进行了仿真实验，验证该方法的可行性。该方法对精度要求较低的松协调运动任务有很大研究价值。

由于NAO机器人本身精度较低，因此在下一步研究中，需要进一步改进松协调控制方法，提高NAO机器人的定位精度，更好地完成松协调运动。

[1] 丁希仑.拟人双臂机器人技术[M].北京:科学出版社,2011.

[2] JU Zhang-feng, YANG Chen-guang, MA Hong-bin. Kinematics modeling and experimental verification of baxter robot[C]. Proceeding of the 33rd Chinese Control Conference,Nanjing:IEEE,2014.

[3] KOCK S, VITTOR T, MATTHIAS B, et al. Robot concept for scalable, flexible assembly automation: a technology study on a harmless dual-armed robot[C].2011 IEEE International Symposium on Assembly and Manufacturing,Tampere:IEEE,2011.

[4] STOLT A, LINDEROTH M, ROBERTSSON A, et al. Force controlled robotic assembly without a force sensor[J].IEEEInternationalConferenceonRoboticsandAutomation,2012,44(8):1538-1543.

[5] SHAMSUDDIN S, ISMAIL L I, YUSSOF H, et al. Humanoid robot NAO: review of control and motion exploration[C].2011 IEEE International Conference on Control System, Computing and Engineering, Penang:IEEE, 2011.

[6] SHAMSUDDIN S, YUSSOF H, ISMAIlL L, et al. Initial response of autistic children in human-robot interaction therapy with humanoid robot NAO[J].IEEEInternationalColloquiumonSignalProcessingandItsApplications,2012,79(4):188-193.

[7] 艳 涛.汇童机器人第4、5代集体亮相[J].机器人技术与应用,2012(4):44.

[8] FITZGIBBON A, PILU M , FISHER R B. Direct least square fitting of ellipses[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1999,21(5):476-480.

[9] 徐 德,谭 民,李 原.机器人视觉测量与控制[M].北京：国防工业出版社,2011.