对分治法解决三维最近点对问题的优化
2018-03-15李俊杰楼吉林
李俊杰,楼吉林
(浙江农林大学暨阳学院,诸暨 311800)
0 引言
三维最近点对问题,是指如何在三维坐标系中找出一对距离最近的点。该问题是计算机算法、计算几何中的经典问题,在图像处理、空中交通管制、智能交通、化学反应、物理变化、材质检测、天文观测等领域都有广泛应用,确定性算法可以达到O(nlogn)的时间复杂度[1]。
三维最近点对问题可以描述为:在空间集合S中,存在n个点依次记为P1,P2,...,Pn(n≥3)。其中任意的Pi与Pj(j≠i)组成一个点对,该点对距离记为dij,求所有点对距离中的最小距离dmin=min{dij(Pi,Pj)|Pi∈S,Pj∈S}。由Pi和Pj所组成的最近点对可能多于一对,本文只讨论如何求出一对点对的情况。
1 问题分析
在解决三维最近点对问题之前,我们可以通过二维最近点对问题的算法来进行类比,第一步采用分治法对空间进行划分。例如,在三维坐标系V中,存在n个点依次记为P1,P2,...,Pn(n≥3),为了将这n个点尽可能均匀的划分到两个空间V1和V2中,可以先计算点集中各点x轴的中位数,并构造一个垂直于x轴的平面x(P)=k来作为分割平面[2]。其中空间V1={x(Pi)≤kx|Pi∈V,k∈N},V2={x(Pj)>kx|Pj∈V,k∈N}。通过递归算法,计算出V1和V2中的最小点对距离的d1和d2,令dm=min{d1,d2}。
第二步同样类比二维情况,求出dl=min{dij(Pi,Pj)|Pi∈V1,Pj∈V2},即在 V1 与 V2 中各取一点,所组成的最近点对距离。其方法是:在第一次进行分割的原分割面kx的基础上做两个与之平行的切面x1=kx+dm与x2=kx-dm(k∈N),将属于两切面之间的点按照z轴坐标进行排序。故属于x1≤xi≤kx范围内的点Pi(xi,yi,zi)所能组成最短距离的另一个端点Pj(xj,yj,zi)一定存在以下关系:kx≤xj≤x2;同时易知,与 Pi组成最近点对的另一端点Pj一定在以Pi为球心,以dm为半径的半球面内,即{sqrt((xi-xj)2+(yi-yj)2+(zi-zj)2)≤dm|xj>xi}。故只要找出上述两式的集合,即可得出需要进行判别的端点Pj所属的范围。但由于计算机进行上述操作所耗费的时间远远大于预期,以至于不能直接进行运算,于是需要采用更加巧妙的方法。不难发现,Pi和Pj中的点具有以下稀疏的性质[3]:对于Pi中的任意一点,Pj中的点必定落在一个dm*2dm*2dm的长方体中。从上述分析可以想到利用该半球面的外接长方体(dm*2dm*2dm)来代替球面进行判断,来减小计算量。随后,只要逐次比较kx≤xj≤x2空间与该外接长方体空间的交集空间内的所有点即可得到以Pi,Pj为端点的最短距离。
不过,直接利用外接长方体对Pj进行筛选,会造成少量多余的计算,每进行一次距离运算,则至少进行了5次加法运算与3次乘法运算,增加了算法在时间上的消耗。那么根据硬件的实现原理,如果可以将一部分的乘法运算转化成运算速度更快的加法运算,则能够在一定程度上提升算法效率。如图1所示。

图1 点Pi判别空间的切割图
对半球面的外接长方体进行切割,四个切割面用虚线表示(图中只给出了两个)分别为可以看出,四个切割面以外的空间是不需要进行计算的。令时,待运算的点Pj可以直接排除。由于鸽舍原理,在未进行切割时dm*2dm*2dm的长方体中最多仅能存在24个满足条件的点[3]。通过计算可以得到未切割时所求长方体体积为4dm3,所切割部分为图2所示的阴影部分。
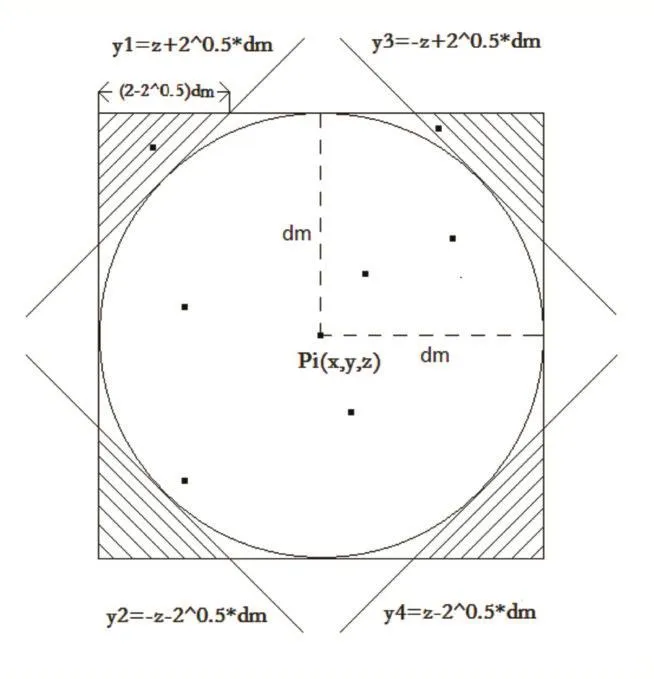
图2 点Pi判别空间的切割面侧视图
第三步,dmin=min(dl,dm)即为在三维坐标系V中,这n个点所组成点对的最小距离。
2 算法设计
2.1 算法描述
通过上述的分析,可以得到分治法求三维最近点对函数Part3()的伪代码如下:


2.2 算法复杂度分析
在算法Part3的第一步中,进行了查找各点x轴坐标的中位数并进行划分的操作,易知时间复杂度为O(n)[3]。
第二步为递归运算,满足公式T(n)=2T(n/2)+O(n),n≥4,且假设 n=2的 k次方,可证:
T(n)=2T(n/2)+O(n)
=2T(n/4)+2O(n/2)+O(n)
=...
=O(n)+O(n)+...+O(n)+O(n)+O(n)
=k*O(n)
=O(k*n)
=O(nlog2n)
即第二步算法的时间复杂度为O(n*logn)。
第三步为常数时间。
第四、五步在分治操作之前采用了预排序,对点集的y轴和z轴分别进行了快排操作,可知时间复杂度为 O(n)。
第六步根据鸽舍原理可得,在判别空间内最多只需要对有限的24个点进行扫描,且在加入判断条件的前提下,大约可以减少1/6的运算量,因此此处的时间复杂度亦为O(n)。
第七步为常数时间。
综上所述,该优化算法整体的时间复杂度为O(n*logn),相较于经典的三维最近点对算法,优化的地方在于:将部分乘法运算转化成了加减法运算,提升了端点在不同区域内计算距离的速度;排除了距离运算公式因重复进行迭代法而产生的时间冗余,减少了距离计算所耗费的时间。
[1]Shamos M I,Hoey D.Closest-Point Problems[C].Foundations of Computer Science,1975.Symposium on.IEEE,1975:151-162.
[2]胡金初.空间最近点对的计算机算法研究[J].计算机科学,2008,35(1):233-235.
[3]王晓东.计算机算法设计与分析[M].电子工业出版社,2012.
