一种融合个体属性与社交关系的民航旅客价值度量方法

丁建立，刘晓庆，王家亮

1.中国民航大学 计算机科学与技术学院， 天津 300300 2.中国民航大学 天津市智能信号与图像处理重点实验室，天津 300300

随着中国经济的高速增长和国民收入的普遍提高，民航已不再仅仅是高收入人群的出行选择，而是成为了一种大众化、平民化的出行方式，民航和铁路之间以及各航空公司之间的竞争日趋激烈。旅客资源的质量和数量成为航空公司致胜的关键，因此对旅客的细分和研究[1-4]成为当前的研究热点。如何评估旅客价值、挖掘旅客关系及发现潜在高价值旅客，成为各航空公司抢夺旅客资源、提高核心竞争力的重要因素。

目前国内外对于民航旅客价值的研究主要集中在旅客个体价值层面，通过构建RFM(Recency, Frequency, Monetary)模型，根据旅客乘机时间近度系数R、乘机频率F、花费金额M等特征，综合计算旅客个体当前实际产生的价值[5]。为了挖掘旅客潜在价值，徐冰宇等提出构建旅客-航线二部图[6]，基于随机游走预测旅客未来出行概率，计算旅客潜在价值，但该模型仅考虑了旅客与航线的关系，忽略了旅客与旅客之间的相互影响。

2014年韩敏提出旅客价值排序Passenger Rank算法[7]，认为旅客除了个体价值外，其在社会网络中的影响价值也应该考虑在内，该算法分别计算旅客独飞价值和网络价值并加权求和获得旅客总价值，但其将独飞价值作为旅客个体价值，而实际上旅客独飞和共飞时自身消费的所有价值都应该属于旅客个体价值，且在计算旅客网络价值时，只考虑了旅客拓扑关系，忽略了旅客个体价值的差异导致的影响力差异，仅根据拓扑结构计算节点的网络价值，不够准确和全面。

目前国内外对于民航旅客关系网络构建和旅客价值度量的研究存在以下问题：首先，民航旅客关系网络的构建只局限于分析PNR(Passenger Name Record)数据，通过旅客同订单关系，计算旅客间乘机关联度以量化旅客关系[8]，而实际上，旅客间存在同一订单的显式关系和不同订单的隐式关系，而不同订单的隐式关系更具挖掘价值；其次，对旅客价值度量的方法过于简单和单一，没有综合考虑旅客个体价值及其在社会关系网络中的相互影响，而旅客价值既取决于个体价值又受其社交关系的影响。

为了解决以上问题，本文提出了一种融合个体属性与社交关系的民航旅客价值度量方法，采用改进的RFMc(Recency, Frequency, Monetary, cab class)模型计算旅客个体价值并根据多关系评价(Multi-Relationship Evaluation,MRE)模型获得旅客关系系数，构建旅客社交关系网络，采用PageRank算法模型模拟旅客价值的网络传递，最终实现可动态调整旅客个体价值和社交关系权重系数的旅客价值度量方法。

1 PageRank算法

PageRank算法最初用于解决页面排序问题，它基于网页之间的链接，根据全局网页的链接情况计算各个网页的重要程度。PageRank算法认为，在Web图模型中一个网页入链数量越多，则该网页越重要；链入该网页的网页质量越高，则该网页越重要。即网页的质量由链入该网页的数量和质量共同决定，这就是PageRank算法的数量和质量假设。

基于以上两个假设，PageRank算法首先赋予所有网页相同的初始重要性得分，其次通过公式ri+1=Mri迭代计算来更新每个网页的PageRank得分，直到得分趋于稳定，获得最终的重要性得分结果，其中r为网页重要性得分向量，M为转移概率矩阵。考虑到一些出度或入度为零的网页(也称为孤立网页)，在原基础上增加了阻尼系数α进行平滑处理，计算公式变为：ri+1=αMri+(1-α)e，其中e表示从任一网页不经过链路而随机跳到任意网页的概率向量。这里假设，用户以等概率跳转到任意网页节点，故e取值为[1/N,1/N,…,1/N]，其中N为网页数量。

PageRank算法的提出吸引了一大批学者对其进行研究，为了解决PageRank算法忽略了主题相关性这一问题，斯坦福大学计算机科学系提出了Topic-sensitive PageRank算法[9]，提高了结果的相关性和主题性，使得用户的个性化查询得以实现。Kamvar等在2003年提出基于块的个性化算法——BlockRank[10]，从更粗粒度的角度提高了算法计算效率。2009年一种基于主题级随机游走的排序算法[11]被提出，解决了Topic-sensitive PageRank算法中需要预定义主题的问题。朱凡微等在2015年提出基于可用性Hub选择的有计划逼近完全个性化PageRank算法[12-13]，使得算法的计算效率和准确度得以动态调整。2016年魏巍等充分运用丰富的节点信息和网络拓扑信息，提出了一种基于多源异构大规模图结构的排序算法[14]，实现了半监督的图节点排序。

PageRank算法的一系列改进使其在对图结构重要节点排序方面具有高可扩展性和高有效性，因此也越来越广泛地被应用于各研究领域，包括关键字提取[15-17]，作者、论文、期刊等网络的节点重要性排序[18-20]等。

与网页排序和其他图节点排序相似，社交网络中的旅客对于航空公司的价值，既包含其个体消费价值，又包含其社交关系价值，综合旅客个体价值和社交关系的综合度量才是对旅客价值的全面度量。况且，旅客成长趋势受其所在社交网络的影响，一个目前个体消费价值较低的旅客与高价值旅客关系越亲密，其消费潜力越大，未来成长为高价值旅客可能性就越大。基于这一思想，本文充分挖掘旅客订票和离港数据，通过RFMc模型计算旅客个体价值，并通过MRE模型分析旅客关系，构建民航旅客社交关系网络，充分利用PageRank算法在大规模图节点排序中的高效性和高可扩展性，设计实现民航旅客价值排序(Civil Aviation Passengers Value Rank, CAPV-Rank)算法，通过旅客间的价值传递模拟真实世界里旅客间的相互影响，并通过权重因子动态调整旅客个体价值和社交关系对旅客价值度量的权重系数，实现旅客个体价值计算、旅客网络价值计算、融合旅客个体价值和网络价值的混合计算等多种旅客价值度量模式，并根据旅客当前个体价值和社交关系预测旅客未来价值，进而挖掘潜在高价值旅客。

2 民航旅客社交关系网络模型和CAPV-Rank算法

定义1民航旅客社交关系网络：被定义为无向加权网络G=(P,E,V,W)，P为所有旅客集合，E为所有旅客关系集合，V为所有旅客个体价值集合，W为所有关系权重集合。

民航旅客社交关系网络模型包括旅客个体价值计算(RFMc)模型和多关系评价(MRE)模型，是旅客价值排序CAPV-Rank算法设计的基础。

2.1 RFMc模型

定义2旅客个体价值：根据旅客个体消费数据计算旅客个体对于航空公司的价值，也指旅客对航空公司的利润贡献值。

传统的RFM模型使用顾客消费近度、消费频率和消费金额来综合衡量顾客价值。从PNR数据中可以得到旅客的乘机金额、乘机时间和乘机频率，针对民航的具体情况和特点，引入舱位等级C对应的票价折扣来表示旅客当次消费对航空公司的价值贡献等级，提出RFMc模型计算民航旅客个体价值，其中MC为结合舱位等级计算得到的旅客相对乘机总金额。

2.1.1 旅客相对乘机总金额MC

考虑到民航的特殊性，不同的飞机舱位等级和折扣为航空公司带来的实际盈利率不同，因此在分析旅客消费金额时应区别对待。

将舱位等级C(对应票价折扣)作为票价的权重计算旅客相对消费总金额MC：

(1)

式中：ci为旅客第i次乘机的票价折扣；mi为旅客第i次乘机的票价；k为购票次数。

2.1.2 乘机时间近度系数R

定义3最近乘机时间t：旅客最近一次乘机时间与当前时间(使用该模型计算旅客个体价值的时间)间隔。

定义4乘机平均周转时间t0：旅客相邻两次乘机时间间隔的平均值:

(2)

式中：tsum为旅客总乘机次数；ti为旅客第i次和第i+1次乘机时间间隔；ts为预计算得到的全旅客集的平均周转时间。

定义5乘机时间近度系数R：旅客再次乘机的可能性:

(3)

乘机平均周转时间t0反应了旅客相邻两次乘机间隔的期望值，当最近乘机时间t小于等于平均周转时间t0时，R值为1；当t大于t0时，旅客再次乘机的可能性逐渐降低，R值逐渐减少。

2.1.3 乘机频率F

旅客乘机频率F反应了旅客的活跃度和忠诚度，乘机频率越大活跃度和忠诚度越高，则该旅客对于航空公司的价值越大。

综上，将旅客相对乘机总金额、乘机时间近度系数和乘机频率加权求和，获得旅客个体价值v：

v=ω1MC+ω2R+ω3F

(4)

式中：ω1、ω2和ω3为各指标的权重系数。考虑到各个指标的测量尺度不同，需将MC、R和F标准化后再加权求和。

2.2 MRE模型

旅客同乘关系包含同订单的显式同乘关系和不同订单的隐式同乘关系，MRE多关系评价模型融合订单数据和离港数据，量化旅客显隐式双层关系并融合时间因素进行多关系的综合评价。

2.2.1 旅客同订单关系

定义6旅客同订单关系：指同一订单的旅客关系，旅客的一次同订单关系包括该订单的旅客数量、旅客舱位等级差和订单生成日期。

根据PNR数据构建全体旅客的同订单关系，用Pij表示旅客i和旅客j的同订单关系序列，Pij[k]={|[ci[k]-cj[k]|,s[k],tp[k]}是序列中的第k项纪录，表示旅客i和旅客j第k次同订单的订单数据，其中：s[k]为该订单的旅客数量，tp[k]为该订单生成日期，ci[k]为该订单中旅客i的舱位等级(对应票价折扣)。

(5)

式中：sp[k]为旅客i和旅客j第k次同订单关系得分。

2.2.2 旅客同乘关系

定义7同乘关系：指乘坐同一航班的旅客关系，包括碰巧同乘关系和约定同乘关系。一次同乘关系包括该次同乘的航班起飞日期、旅客座位距离、值机序号距离、舱位等级差等属性。

据离港数据构建全体旅客的同乘关系，用Dij表示旅客i和旅客j的同乘关系序列，Dij[k]={|[dci[k]|,|dseat[k]|,|dclass[k]|,td[k]}是序列中的第k项纪录，表示旅客i和旅客j第k次同乘时的航班数据，td[k]为该航班起飞日期，dci[k]为旅客i和旅客j的值机序号距离，dseat[k]为旅客i和旅客j航班座位的欧氏距离，dclass[k]为旅客i和旅客j的舱位等级差。

(6)

(7)

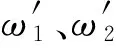
2.2.3 融入时间因素的多关系综合评价

旅客价值按照边权不均匀传递，旅客关系越亲密边权越大则获得的传递价值越大，因此边权计算的科学性、准确性直接影响旅客价值度量结果。

RFM模型根据顾客消费近度系数R预测顾客再次消费的可能性。同样，对于民航旅客，本文认为旅客关系也具有时间相关性：最近同行过的旅客，再次同行的可能性更大，关系更亲密；相反，即使曾经同行多次，但近两年都没有同行记录，也要考虑是否该旅客关系已经消失。基于以上考虑，设定观测时间窗口，观察时间窗口内的旅客关系，引入时间衰减因子τ，使得旅客关系具有时间感知性。

假设旅客旅客i和旅客j最后一次同订单(或同乘)时间为t，则旅客i和旅客j同订单(或同乘)关系的时间衰减因子τ可表示为

(8)

式中：T-t′为观测时间窗口的长度；T为时间窗口的结束时间；t′为时间窗口的起始时间。t≤t′表示在观测时间窗口内旅客未发生同订单(或同乘)关系，则认为该关系消失，令τ=0。

引入时间衰减因子后，旅客同订单关系得分可表示为式(9)，旅客同乘关系得分为式(10)：

(9)

(10)

式中：τPij为旅客i和旅客j同订单关系的时间衰减因子；τDij为旅客i和旅客j同乘关系的时间衰减因子。

将旅客同乘关系得分和同订单关系得分规范化后加权求和，获得旅客关系总得分。计算公式为

(11)

式中：Wij为旅客i和旅客j的关系总得分；ωp、ωd分别为同订单关系权重、同乘关系权重，ωp<ωd。

2.3 CAPV-Rank算法设计

2.3.1 传统PageRank算法

有个成语叫狡兔三窟，那是指动物们。现代某些贪官，狡猾地常爱玩脚踏两只船的伎俩。他们的攀援术是谁有用就依附谁，多头出击。他们认为，“脚踏两只船”是一种生存之道。如果只会死心塌地地踏着一条船划着一支桨独行于风雨之中，实在是有些“虚度了丰富多彩的人生”。这些人，生活的理念是，宝贵的生命可不能在一棵树上吊死。在一艘船里葬身，那多亏！所以，他们的生存之道是，多给自己留条后路，多踩几条船才会无后顾之忧，哪条船更稳上哪条，不损毫发，何乐而不为？

在Web图模型中，网页为节点，网页间的链接关系为边，节点得分即表示网页重要性。节点得分通过边向邻居节点传递，节点i的得分等于其从邻居节点获得的得分总和，表达式为

(12)

式中：ri为节点i的得分；N(i)为节点i的邻居节点；O(j)为节点j的出度。

为了解决悬挂节点，引入阻尼系数α，加入虚链路使节点得分不仅可以从邻居节点沿实际链路传递获得，还可以从任意节点沿虚链路传递获得，节点i得分表达式为

(13)

式中：α为阻尼系数，表示节点沿实际链路继续传递的概率；1-α为沿虚链路随机跳转概率；N为网页数量。

推广至所有节点，节点得分向量计算公式为

(14)

2.3.2 CAPV-Rank算法

1) 引入旅客价值转移概率矩阵M

(15)

式中：N(i)为节点i的邻居节点集。由式(15)可知Mij≠Mji，这是因为虽然Wij=Wji，但旅客i和旅客j自身的社交关系不同，该组关系在各自社交关系中所占的比重不同，因此转移概率不同。

2) 引入个性化转移向量U

在民航旅客社交关系网络G中，V为通过RFMc模型计算得到的旅客个体价值集合，vi表示旅客i的个体价值，定义旅客个性化转移向量为U=[u1u2…un]，n为旅客数量，ui为旅客i的个性化转移概率，表达式为

(16)

传统PageRank算法中所有节点得分和为1，由于旅客数为千万量级，旅客价值规范化和为1会导致各旅客价值极小，不利于收敛性的判定，因此将旅客价值总和初始化为n。

3) 融合旅客个体价值和社交关系计算旅客i的价值得分ri为

(17)

式中：阻尼系数α用来调整社交关系和旅客个体价值对旅客价值度量的影响程度，0≤α≤1。

4) 推广至全旅客集，融合旅客个体价值和社交关系计算旅客价值得分向量，即

(18)

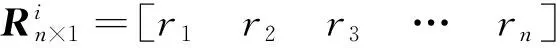
设置迭代终止条件为

‖Ri+1-Ri‖2≤ε

PageRank算法收敛性已得到证明，CAPV-Rank算法只是基于PageRank算法做了参数调整，显然也是收敛的。无论赋予怎样的初值，最终R会趋于一个稳定值，即为旅客价值。

3 网络模型构建中的问题和算法讨论

3.1 旅客身份识别

由于PNR和离港数据中旅客证件信息庞杂，同一旅客每次乘机可能使用不同的证件信息。为了准确计算旅客个体价值和评价旅客关系，旅客身份识别成为网络模型构建中首要解决的关键问题。

本文将PNR数据进行数据关联和身份聚合，构建旅客证件信息列表，添加旅客序列号PSG_ID作为旅客的唯一标识，如表1所示。

其中旅客序列号[1,2,3,…,n]是旅客的唯一标识，证件号均进行过加密处理。由表1可知，旅客1对应3种证件类型和3个证件号。

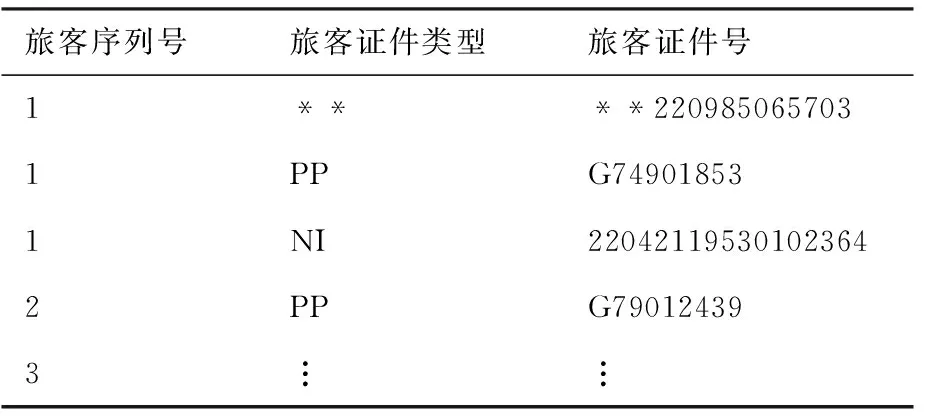
表1 旅客证件信息列表样例Table 1 Example of passenger document information

3.2 旅客关系识别

3.2.1 删除假隐式关系

由于旅客隐式同乘关系有的特征明显，例如值机序号相连且座位相邻，据此可以判断这两位乘客可能是约定的同乘关系，具有一定的社会关系；有的隐秘不易被发现，例如虽然同乘时座位和值机序号不都相邻，但是同乘多次，据此也可判断乘客之间有一定的社会关系；还有些旅客同乘关系仅有一次，且该次同乘中座位号或值机序号不都相邻，本文认为这种情况极可能是碰巧同乘而旅客双方并不存在社会关系。

因此，结合构建好的旅客同乘关系和同订单关系，若两位旅客不存在同订单关系，同乘关系仅有一次且该次同乘值机序号和座位号不都相邻，则将这两位旅客视为碰巧同乘并将二者之间的同乘关系删除。

3.2.2 保护真实旅客关系

有些多于两人的小团体出行，内部成员不可能两两都座位相邻、值机序号相邻，但其存在一定的社会关系，为保护这些真实旅客关系不被误认为假隐式关系，需要在构建旅客同乘关系时，首先识别离港数据中的同行小团体，并将团体内部成员之间的所有同乘关系均设置为值机序号相邻且座位相邻。

3.3 模型中的参数设置

对于式(4)中RFMc指标权重的分配问题，由于行业背景不同、对客户的关注层面不同，因而没有统一的分配方案。在民航背景下，旅客个体价值体现在旅客对于民航利润的贡献值，而旅客相对乘机金额MC是旅客实际消费贡献值的直观体现，对民航收益影响最大；其次，旅客乘机频率F反映了旅客的活跃度和忠诚度，是旅客价值度量需要考虑的重要因素；最后，综合旅客消费近度系数R和旅客平均周转时间可以预测旅客再次乘机的概率。因此在民航旅客个体价值计算的权重分配中，应遵循值度最重、频度次之、近度最次的原则。

对于式(8)，本文将时间窗口长度设为两年，表示若旅客在最近两年内没有发生同乘(或同订单)关系，则认为旅客关系消失，将曾经积累的关系清零。例如：在2016年5月1日使用本模型评价旅客关系，设定时间窗口为两年，则时间窗口结束时间T为2016-05-01，起始时间t′为2014-05-01。若旅客i和旅客j最后一次同订单(或同乘)时间为2015年5月1日，则t=2015-05-01，计算可得τ=365/730=0.5，若t≤t′，表示旅客在观测时间窗口内没有发生同订单(或同乘)关系，即令τ=0。由于本文使用的训练数据集为一年的数据，时间窗口设为2年，因此τ值均大于0.5。实际应用中，时间窗口的长度可视情况而定。

3.4 CAPV-Rank算法讨论

CAPV-Rank算法既可用来进行多模式下的旅客价值度量，又可用来预测旅客未来价值的变化趋势，挖掘潜在高价值旅客。

3.4.1 旅客价值度量

旅客价值度量帮助航空公司进行旅客管理并制定各种营销策略，基于不同的业务需要，旅客价值度量的出发点和立足点不同，则度量标准不同。

CAPV-Rank算法可以通过调节α权重因子，灵活调整旅客个体价值和社交关系对旅客价值度量的影响系数：

1) 当α=0时，Ri+1=αMRi+(1-α)U=U，忽略了社交关系对旅客价值的影响，仅通过RFMc模型分析旅客个体实际消费情况来度量旅客价值。与传统RFM相比，RFMc模型考虑了舱位等级不同而带给航空公司不同的利润价值，更适用于民航背景下的旅客价值计算。

2) 当α=1时，Ri+1=αMRi+(1-α)U=MRi，忽略了旅客个体价值，仅根据旅客之间的社交关系采用改进的PageRank算法模型衡量旅客价值。与传统带权PageRank算法不同的是，本文构建旅客社交网络时，分析了PNR数据和离港数据双数据源，对旅客关系挖掘得更彻底进而价值度量更全面。

3) 当0<α<1时，Ri+1=αMRi+(1-α)U，是融合了旅客个体价值和社交关系的混合度量方法，真正将个体价值融入社交关系网络并使其参与到旅客价值迭代计算的过程中，对旅客价值度量更全面，且通过α动态调整旅客个体价值和社交关系的权重，满足多变的业务需求。

3.4.2 旅客价值预测

1) 预测旅客个体价值，挖掘潜在高价值旅客

CAPV-Rank算法认为旅客价值受其所在社交网络的影响，当前价值较低的旅客与高价值旅客联系越紧密，消费潜力越大，未来成为高价值旅客的概率越大，因此根据旅客当前个体价值和社交关系预测旅客未来个体价值，通过参数α控制社交关系对旅客价值的影响系数，根据训练数据和测试数据寻求最佳的α，使其达到较好的预测效果。

根据参数确定后的式(18)计算得到旅客个体价值的预测结果为Rn×1=[r1r2…rn]T，Un×1=[u1u2…un]T为旅客当前个体价值，则旅客的潜在价值向量Tn×1为

Tn×1=Rn×1-Un×1

(19)

从Tn×1中选择最大的前k个值，即为潜在价值最大的k个旅客。

2) 预测旅客价值相对生长速度

旅客价值相对生长速度是旅客增加的价值和原有价值的比值，当前个体价值越小而潜在价值越大，潜在价值相对生长速度越快。定义旅客潜在价值相对生长速度为RT，表达式为

(20)

从RT中选择最大的前k个值，即为相对生长速度最快的k个旅客。与旅客潜在价值预测相比，预测旅客相对生长速度，更有助于发现当前价值很小而潜在价值相对较大的旅客。

4 实验与分析

4.1 实验数据

本文实验用到的数据来自于民航订座系统中2015、2016年旅客订票(PNR)数据和离港(Departure)数据，其中PNR数据集中每一行是一个旅客关于某次行程的订票记录，Departure数据集中每一行是一个旅客关于某次行程的离港记录。考虑到本文提出的旅客价值度量模型依赖于旅客真实的社交关系网络，对网络的完整性要求较高，因此以中国某航空公司为研究目标，从订座系统的全数据集中提取出该航空公司2015、2016两年都有乘机记录的全旅客出行数据集，该数据集共有旅客2千多万名，旅客出行记录1.6亿多条，其中2015年7千多万条，2016年8千多万条。

共生成3个数据集：D1(2015年全旅客出行数据集)，D2(2016年全旅客出行数据集)，D3(2015和2016两年的全旅客出行数据集)。

根据3.1节构建的旅客证件信息列表，将数据集中的旅客证件号替换为对应的旅客序列号PSG_ID，作为旅客的唯一标识。同时，为方便计算旅客个体价值，将数据集中的舱位等级代码替换为各代码对应的票价折扣，其中头等舱票价为全价的1.5倍，公务舱票价为全价的1.3倍，超级经济舱票价等于全价的1倍，其他普通经济舱为全价的0.95～0.25倍不等。

4.2 基准算法

1) RFMc模型。根据旅客历史消费记录，获得旅客乘机时间近度系数R、乘机频率F和消费金额M度量旅客价值。

2) 加权PageRank算法。分析PNR数据，根据旅客历史订单构建旅客同行关系网络，将旅客同订单次数作为边权重，使用加权PageRank算法度量旅客价值。

3) Passenger Rank算法[7]。该算法分为两个独立过程：使用RFMc模型计算旅客价值，将独飞次数占乘机总次数的比例与旅客价值相乘作为旅客个体价值；使用加权PageRank算法计算旅客网络价值，最后将两部分加权求和得到旅客总价值。

Passenger Rank算法使用RFM算法与加权PageRank分别单独计算旅客个体价值与网络价值再求和，在计算旅客个体价值和网络价值时都具有局限性：首先，旅客个体价值是旅客个体消费带给航空公司的利润价值，因此无论是旅客独飞还是与他人同行，旅客本身花费的机票价格都应该归为其个体价值；其次，不同于其他行业，不同舱位等级为航空公司带来较大的利润差异，也体现了旅客不同的消费水平，因此也应该作为旅客个体价值的衡量标准之一；最后，计算旅客网络价值时，不仅应该考虑旅客关系的强弱，还要考虑旅客因个体消费水平不同对网络的影响力也截然不同。

4) 随机游走算法。随机游走算法通过分析旅客个体出行数据，构建旅客-航线二部图网络，再使用随机游走模型预测旅客未来可能选择的航线，最后根据航线价值预测旅客未来价值。

4.3 算法功能分析和实验设计

CAPV-Rank算法融合了旅客当前个体价值和社交关系，既可用于旅客价值度量又可进行旅客个体价值预测：① 进行旅客价值度量时，参数α控制旅客个体价值和社交关系对于旅客价值度量的权重分配，参数α的设置主要依托于具体的业务背景和目的，可以根据需要进行调整；② 进行旅客个体价值预测时，参数α协调旅客个体消费的稳定性和社交关系对旅客价值的影响，可以根据训练数据和测试数据寻求最佳的α，以达到更好的预测效果。

4.3.1 对旅客价值的度量

由于旅客价值是不确定的概念，且在不同的业务需求、业务背景下，由于出发点和立足点不同，对旅客价值的度量标准也不同，因此很难直接证明本文提出的CAPV-Rank算法对旅客价值度量的准确性优于其他算法，但就算法灵活性和稳定性而言，CAPV-Rank算法明显优于其他算法。

1) 算法灵活性

当前业界对民航旅客价值的研究主要有旅客个体价值度量和网络价值度量。与传统度量方法不同的是，CAPV-Rank算法可以通过调节参数α，实现多种旅客价值度量模式，如3.3.1节所述，在α=0时实现旅客个体价值度量，在α=1时实现旅客网络价值度量，在0<α<1时实现融合旅客个体价值和社交关系的混合价值度量，且在各种模式下，都优于现有算法。

2) 混合价值度量的稳定性

仅根据旅客实际个体消费数据计算旅客个体价值具有滞后性，且由于旅客短期消费不稳定，使得旅客价值计算结果稳定性较差；而融合了旅客个体消费水平和社交关系的总体价值，在事实消费数据的基础上结合旅客社交关系综合度量旅客价值，社交关系的影响减弱了旅客个体短期不稳定消费对旅客价值度量的影响，因而对旅客价值度量稳定性更好。

综上，在旅客价值度量方面主要检验：① 参数α对旅客价值度量结果的影响；② CAPV-Rank算法的稳定性与其他基准算法的稳定性比较。

4.3.2 对旅客个体价值的预测

1) 混合算法具有前瞻性，可以根据旅客当前个体价值和旅客社交关系预测旅客未来个体价值，α为进行旅客个体价值预测时，旅客受社交关系的影响系数，也可以称为旅客向邻居旅客学习的步长因子，α越大，社交网络对旅客价值预测结果影响越大。

2) 根据旅客个体价值的预测结果，挖掘潜在高价值旅客和高生长速度旅客。

因此，对旅客价值预测主要检验：① 参数α对旅客个体价值预测准确性的影响；② 算法对潜在高价值旅客挖掘和高生长速度旅客发现的准确性与基准算法的比较。

4.4 算法评价指标

本文采用Spearman等级相关系数作为旅客价值度量稳定性和旅客个体价值预测准确性的评价指标，采用Jaccard相似系数作为潜在高价值旅客挖掘和潜在高生长速度旅客发现的准确性评价指标。

4.4.1 Spearman等级相关系数

Spearman等级相关系数用来估计两个变量X、Y之间的相关性，如果两个变量取值的两个集合中均不存在相同的两个元素，那么当其中一个变量可以表示为另一个变量的很好的单调函数时，两个变量之间的相关系数可以达到+1或-1。

斯皮尔曼等级相关系数f计算公式为

(21)

本实验中的Xrank为待检验算法(基准算法或者不同α下的CAPV-Rank算法)在数据集D1上计算的旅客价值向量R1的排序结果向量，其中Xrank i为第i个旅客价值在Xrank中的排名。Yrank在进行不同实验时，分别为：① 进行α因子的影响检验时，Yrank为不同α下的CPAV-Rank算法在数据集D1上计算的旅客价值向量R1的排序结果向量；② 进行算法稳定性检验时，Yrank为待检验算法在数据集D3上计算的旅客价值向量R3的排序结果向量；③ 进行旅客个体价值预测的准确性检验时，Yrank为待检验算法数据集D2上计算得到旅客个体价值向量U2的排序向量。其中Yrank i为第i个旅客价值在Yrank中的排名。

Spearman等级相关系数越大，说明采用该算法在两个数据集上计算结果的相关性越大，算法稳定性越好，对旅客个体价值预测越准确。

4.4.2 Jaccard相似系数

Jaccard相似系数核心思想是计算两个集合A和B的交集元素在A，B的并集中所占的比例，用符号J(A,B)表示。其具体定义为

(22)

本实验中集合A是指由待检验算法在数据集D1上输出的旅客潜在价值列表T(或相对生长速度列表RT)中潜在价值(或相对生长速度)最大的k个旅客，而集合B是在数据集D1和D2上计算旅客价值U1和U2，获得旅客实际个体价值变化UG=U2-U1(或旅客实际相对生长速度向量UG/U1)，取出值最大的k个旅客生成的集合。

J(A,B)越大(最大值为1)表示集合A与集合B相同的元素越多，也即算法预测准确性越好。

4.5 实验与结果分析

实验共分为两部分：① 检验参数α对算法性能的影响；② 比较本文提出的算法与基准算法在旅客价值度量方面的稳定性和预测的准确性。

4.5.1 参数α对算法性能的影响

1) 对旅客价值度量结果的影响

令α=(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1)计算旅客价值，并与使用RFMc模型得到的旅客价值做Spearman等级相关性分析，结果见图1。

当α=0时，R=U，与通过RFMc模型计算旅客个体价值结果相等，故相关性为1。随着α的增加，CAPV-Rank算法与RFMc算法计算结果相关性逐渐减弱。

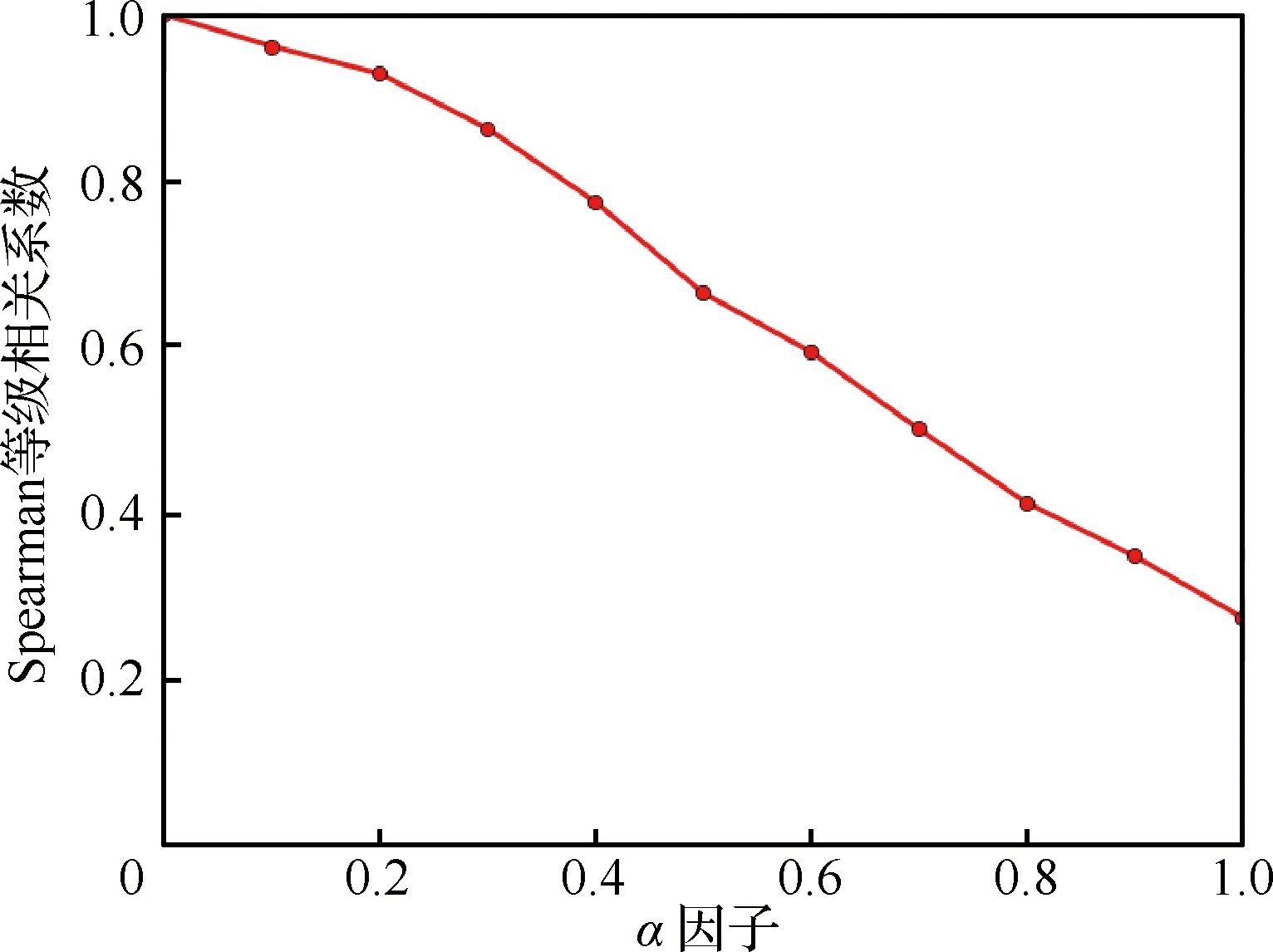
图1 α因子对计算结果的影响Fig.1 Influence of α on calculation result

2) 对预测结果准确性的影响

在不同α下使用CAPV-Rank算法计算旅客个体价值，并与第2年旅客真实个体价值做Spearman等级相关性分析，结果见图2。

由图2可以看出当α=0.4时，CAPV-Rank算法在旅客个体价值预测效果最好，因此令α=0.4，在实际应用中，为达到最佳的预测效果，可以进行更细致的参数寻优。

4.5.2 与基准算法的比较

1) 旅客价值度量

分别采用α=0.4下的CAPV-Rank算法、Passenger Rank算法[7]、加权PageRank算法和RFM模型在数据集D1和数据集D3上进行民航旅客价值计算，将计算结果进行Spearman等级相关性分析，Spearman等级相关系数越大，对旅客价值度量的稳定性越好，结果见表2。

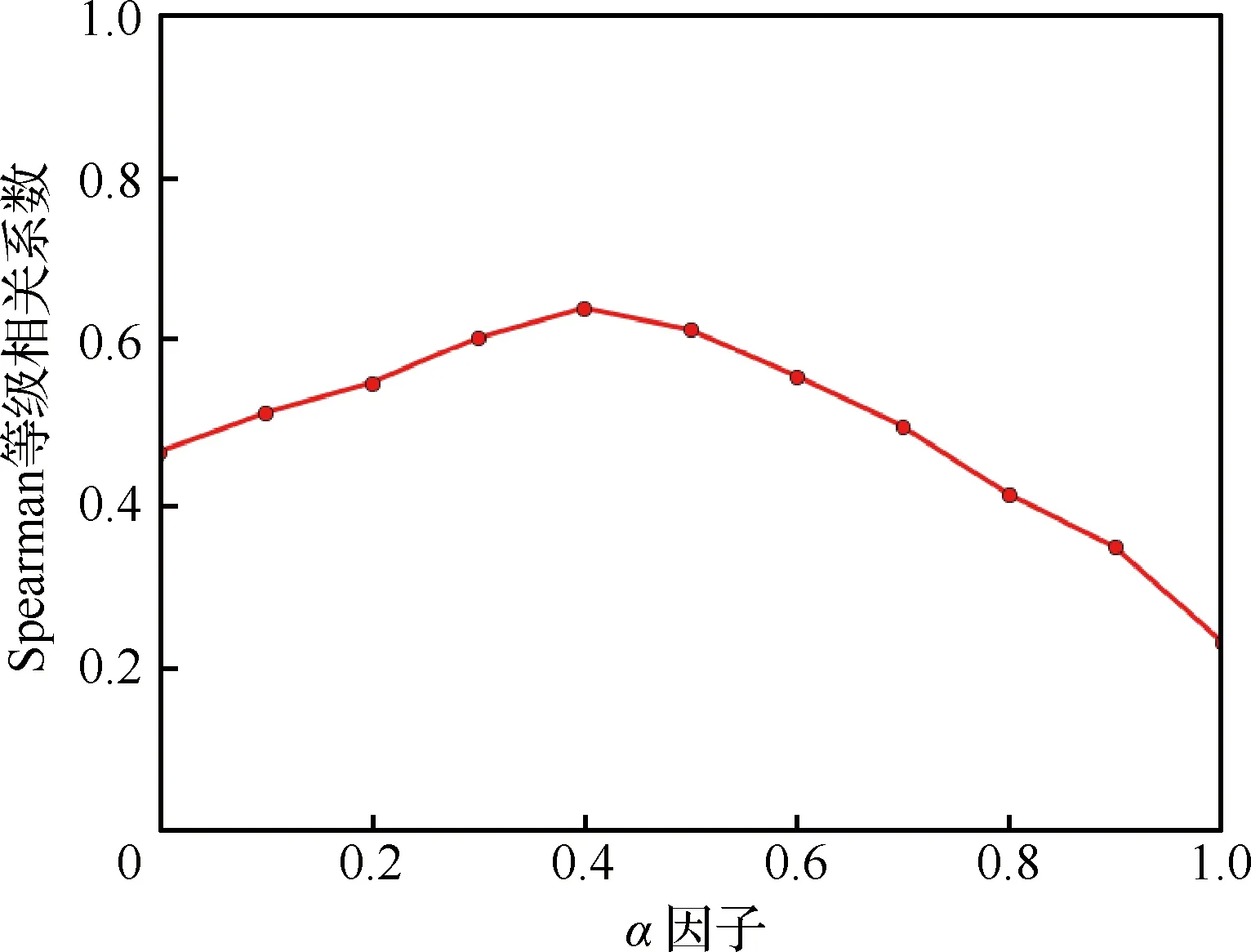
图2 不同α下预测结果的准确性Fig.2 Accuracy of the prediction with different α

表2 度量结果的稳定性Table 2 Stability of measurement results

算法Spearman等级相关系数CAPV-Rank算法(α=0.4)0.822PassengerRank算法0.781加权PageRank算法0.544RFM模型0.693

2) 旅客个体价值预测

分别将采用α=0.4下的CAPV-Rank算法、Passenger Rank算法[7]、加权PageRank算法和RFM模型在数据集D1上进行旅客个体价值计算的结果与在数据集D2采用各自算法计算的旅客个体价值结果进行Spearman等级相关性分析，Spearman等级相关系数越大，对旅客个体价值预测的准确性越好，结果见表3。

随机游走算法[6]建立旅客-航线二部图网络，通过预测旅客未来可能选择的航线来计算旅客潜在价值，该算法只考虑旅客与航线的关系，忽略了同行旅客之间的相互影响，而且由于绝大多数旅客出行数据极少，导致预测准确率较差。CAPV-Rank算法综合考虑旅客个体消费水平和同行旅客的影响，对旅客潜在价值具有更好的预测效果。

由表2和表3可以看出，CAPV-Rank算法与其他算法相比，度量稳定性和预测准确性更好。

表3 对旅客个体价值预测的准确性Table 3 Accuracy of individual value prediction

3) 潜在高价值旅客挖掘

分别使用CAPV-Rank算法、随机游走算法在数据集D1上计算旅客潜在价值，将计算结果与旅客真实价值变化结果作Jaccard相关性分析(k=2 000 000)，结果见表4。

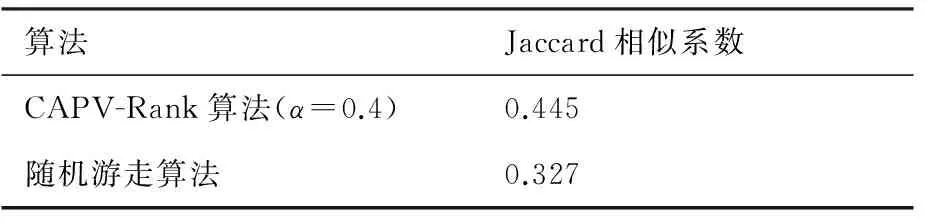
表4 潜在价值预测的准确性Table 4 Accuracy of potential value prediction

4) 潜在高生长速度旅客发现

分别使用CAPV-Rank算法、随机游走算法在数据集D1上预测旅客价值相对生长速度，将预测结果与旅客真实价值相对生长速度结果作Jaccard相似性分析(k=2 000 000)，结果见表5。

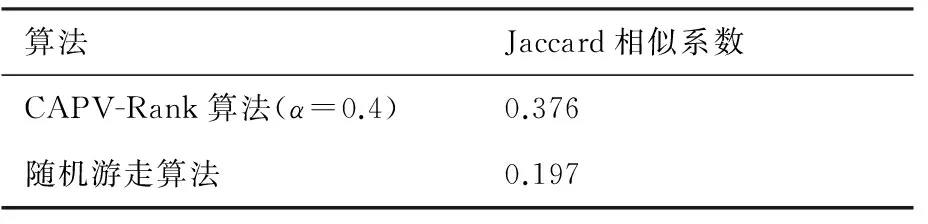
表5 相对生长速度预测的准确性Table 5 Accuracy of relative growth rate prediction

与潜在价值预测相比，潜在生长速度预测有助于发现当前旅客个体价值更小、潜在价值更大的旅客。随机游走算法仅根据旅客个人消费预测潜在价值，严重依赖于旅客个体消费数据，而个体价值更小的旅客出行数据更少，因此预测准确性更差。CAPV-Rank算法构建旅客社交关系网络，根据旅客真实社交关系预测旅客价值，解决了数据稀疏造成的预测准确率低下的问题，在旅客价值预测、潜在高价值旅客挖掘和潜在高生长速度旅客发现方面更准确。

5 结 论

1) 本文提出的CAPV-Rank算法既可以实现旅客价值度量又可以预测旅客未来个体价值及挖掘潜在高价值旅客。

2) CAPV-Rank算法进行旅客价值度量时，可以根据不同需求和目的，动态调整旅客个体价值和社交关系权重因子，实现旅客个体价值度量、旅客网络价值度量、融合旅客个体属性与社交关系的混合价值度量3种度量模式，适应各种业务场景，满足不同业务需求。

3) 进行旅客个体价值计算时，引入舱位等级C，将传统RFM模型改进为RFMc模型计算旅客个体价值，更适合民航背景下的旅客个体价值度量。

4) 进行混合价值度量时，CAPV-Rank算法在事实消费数据的基础上结合旅客社交关系综合度量旅客价值，社交关系的加入克服了旅客个体短期不稳定消费对旅客价值度量的影响，因而对旅客价值度量稳定性更好。

5) 进行旅客价值预测和潜在高价值旅客发现时，CAPV-Rank算法可以动态调整因子，训练获得使预测效果最佳的步长因子α，有效预测旅客价值、挖掘潜在高价值旅客和高生长速度旅客。

6) 本文深入挖掘多数据源中的旅客关系，构建旅客显隐式双层关系网络，解决了非同订单的旅客同乘关系易被忽略、真实旅客关系难以识别等问题，为今后旅客群体的分类、旅客社交关系识别及旅客行为偏好研究提供了新的解决思路。

[1] 冯霞, 徐冰宇, 卢敏. 民航旅客订票行为细分及群体特征分析[J]. 计算机工程与设计, 2015, 36(8)： 2217-2222.

FENG X, XU B Y, LU M. Booking behavior subdivision and characteristic analysis of civil aviation passenger[J]. Computer Engineering and Design, 2015, 36(8): 2217-2222 (in Chinese).

[2] 潘玲玲. 基于旅客行为的航空旅客细分模型研究及其实现[D]. 南京： 南京航空航天大学, 2012: 1-57.

PANG L L. The research and realization of civil aviation customer segmentation based on customer behavior[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012: 1-57 (in Chinese).

[3] 林友芳, 王琨琨, 周超, 等. 基于社交网络的民航旅客偏好建模[J]. 北京交通大学学报, 2014, 38(6): 33-39

LIN Y F, WANG K K, ZHOU C, et al. Modeling the preference of air passengers based on social network[J]. Journal of Beijing Jiaotong University, 2014, 38(6): 33-39 (in Chinese).

[4] 王坤坤. 民航旅客座位偏好建模与应用研究[D]. 北京： 北京交通大学, 2015: 1-48.

WANG K K. Research of modeling the seat preference of civil aviation passengers and its applications[D]. Beijing: Beijing Jiaotong University, 2015: 1-48 (in Chinese).

[5] 曹卫东, 白亮, 聂笑盈. 基于Map/Reduce的民航高价值旅客发现方法[J]. 计算机工程与设计, 2015, 36(4): 1078-1083.

CAO W D, BAI L, NIE X Y. Method of discovering high-value passengers of civil aviation based on map/reduce[J]. Computer Engineering and Design, 2015, 36(4): 1078-1083 (in Chinese).

[6] FENG X, XU B Y, MIN L, et al. Potential high-value passengers discovery by random walk on passenger-route heterogeneous network[J]. Journal of Computational & Theoretical Nanoscience, 2015, 12(8): 1568-1593.

[7] 韩敏. 基于社会网络的民航旅客价值排序算法研究与实现[D]. 北京： 北京交通大学, 2014: 22-38.

HAN M. The research and implementation on ranking the aviation passengers’ values based on social network[D]. Beijing: Beijing Jiaotong University, 2014: 22-38 (in Chinese).

[8] 冯霞, 李勇, 陈卉敏. 民航旅客社会网络构建方法研究[J].计算机仿真, 2013， 30(6): 51-54, 142.

FENG X, LI Y, CHEN H M. Research on constructing social network of airline customers from data of PNR[J]. Computer Simulation, 2013, 30(6): 51-54,142 (in Chinese).

[9] HAVELIWALA T H. Topic-sensitive PageRank[C]∥International Conference on World Wide Web, 2002：517-526.

[10] KAMVAR S D, HAVELIWALA T H, MANNING C D, et al. Exploiting the block structure of the web for computing PageRank[R]. Palo Alto, San Francisco: Stanford University Technical Report, 2003: 1-13.

[11] YANG Z, TANG J, ZHANG J, et al. Topic-level random walk through probabilistic model[M]∥Advances in Data and Web Management. Berlin: Springer Berlin Heidelberg, 2009: 162-173.

[12] 朱凡微, 吴明晖, 应晶. 高效个性化PageRank算法综述[J]. 中国科技论文, 2012, 7(1): 7-13.

ZHU F W, WU M H, YING J. Efficient personalized PageRank computation: A survey[J]. China Sciencepaper, 2012, 7(1): 7-13 (in Chinese).

[13] ZHU F W, FANG Y, CHANG C C, et al. Scheduled approximation for personalized PageRank with utility-based hub selection[J]. The VLDB Journal, 2015, 24(5): 1-25.

[14] WEI W, GAO B, LIU T Y, et al. A ranking approach on large-scale graph with multidimensional heterogeneous information[J]. IEEE Transactions on Cybernetics, 2016, 46(4): 930.

[15] WAN X, XIAO J. Single document keyphrase extraction using neighborhood knowledge[C]∥National Conference on Artificial Intelligence, 2008: 855-860.

[16] LI D, LI S, LI W, et al. A semi-supervised key phrase extraction approach: learning from title phrases through a document semantic network[C]∥Proceedings of the, Meeting of the Association for Computational Linguistics, 2010: 296-300.

[17] SIDDIQI S, SHARAN A. Keyword and keyphrase extraction techniques: A literature review[J]. International Journal of Computer Applications, 2015, 109(2): 18-23.

[18] MIHALCEA R, TARAU P. TextRank: Bringing order into texts[J]. Unt Scholarly Works, 2004: 404-411.

[19] AMJAD T, DING Y, DAUD A, et al. Topic-based heterogeneous rank[J]. Scientometrics, 2015, 104(1): 1-22.

[20] DING Y. Topic-based PageRank on author cocitation networks[J]. Journal of the Association for Information Science and Technology, 2011, 62(3): 449-466.