基于Magic Formula轮胎模型的动力学试验与建模技术研究

周波 钱留华 李衡

摘要：轮胎特性是研究汽车动力学的基础，特别是轮胎的侧偏特性对汽车的操纵稳定性有着非常重要的影响。而实际应用过程中，由于缺乏轮胎动态力学特性试验及建模技术的研究，轮胎模型参数往往难以获得。本文应用Magic Formula轮胎模型建模方法，从轮胎动态力学特性试验、轮胎模型参数辨识和模型的精度验证等方面开展了深入研究，最终建立了Magic， Formula轮胎模型。并通过相关的仿真与试验研究，验证了该模型的精度及其在极限工况下的仿真能力。

关键词：Magic Formula轮胎模型;轮胎动力学试验;参数辨识;精度验证

1 前言

在汽车动力学研究中，对轮胎模型的准确描述是整车动力学分析的基础。由于汽车行驶时，所有地而作用力都是通过轮胎作用到汽车上，因此轮胎的力学特性对汽车操纵稳定性有着非常重要的意义。特别是轮胎的侧偏特性，它决定车辆操纵稳定性，影响车辆制动安全性、行驶平顺性、前轮摆振和车辆侧向振动等重要特性。因此在对上述车辆动力学特性的分析、仿真研究中，建立一个能够准确描述轮胎特性的轮胎模型，其重要性和必要性是显而易见的^[1-3]。

轮胎模型的构建一般分为两种，一种是理论模型（物理模型），即通过对车轮结构和变形机理的数学描述，建立剪切力和回正力矩与相应参数的函数关系，较有影响的是Cim模型、Fiala模型等。轮胎理论模型是在轮胎物理结构和变形机理研究的基础上建立的对轮胎力和力矩的数学描述，由于理论模型形式复杂，计算效率地，因此在车辆动力学研究中应用有很大困难。另一种是经验公式或半经验公式模型，它是通过对大量的轮胎力特性的试验数据进行回归分析，将轮胎力特性通过含有拟合参数的公式有效地表达出来，比较有影響的是Pacejka提出的Magic Formula（魔术公式）模型以及郭孔辉院士建立的UniTire（幂指数公式）半经验模型。

Magic Formula轮胎模型是1987年由荷兰Delft理工大学的Pacejka教授提出，后被称为“魔术公式”轮胎模型，这是一个基于试验数据的经验轮胎模型，通过大量试验数据拟合得到。试验通过专用的试验台架或试验车进行，这种试验设备能够排除次要因素，模拟出待定的轮胎行驶条件.准确地再现轮胎的各种工作情况。试验过程中用于检测各类数据的仪器要求很高的精度和灵敏度，并配备有功能强大的数据处理系统，从而保证试验数据的准确可靠。Magic Formula轮胎模型只用一套公式就可完整地表达纯工况下轮胎的力学特性，故称之为“魔术公式”，其轮胎力特性的表达准确和简洁，适应工况范围广，在汽车操纵动力学研究应用比较广泛，在现今的轮胎特性描述中，魔术公式越来越占据主导地位，其拟合的精度高，并且在极限值以外的一定范围内仍可应用，并且具有较高的置信度，适合于汽车动力学模拟、控制等领域进行理论分析和预测。因此本文采用Magic Formula轮胎模型进行具体的轮胎特性分析^[3]。

2 Magic Formula轮胎模型介绍

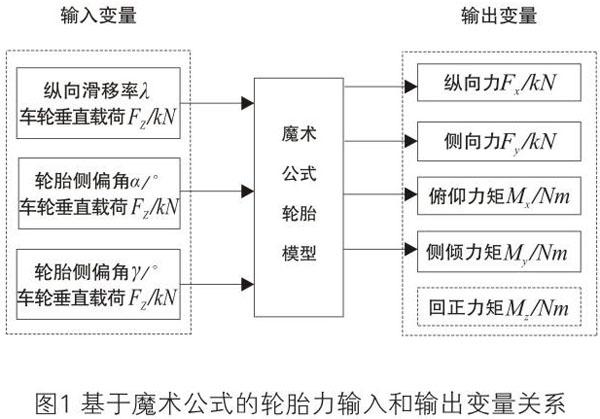
Magic Formula轮胎模型采用SAE标准轮胎运动坐标系，基于魔术公式的轮胎力计算输入和输出变量关系如图1所示：

图1基于魔术公式的轮胎力输入和输出变量关系

Magic Formula是利用三角函数来建立稳态条件下的轮胎纵向力、侧向力和回正力矩模型的，只用一套公式就完整地表达了轮胎的力特性，公式表达如下：

式中，Y为侧向力、纵向力或回正力矩;X为侧偏角或纵向滑移率;D为峰值因子;B为刚度因子;C为曲线形状因子;E为曲线曲率因子;为曲线水平方向漂移;为曲线垂直方向漂移。

3 轮胎动力学试验

轮胎动力学台架试验对设备的精度和灵敏度要求较高，并且对于设备的操作和后期的数据处理，需要深厚的专业知识和经验，国内汽车主机厂一般不具备轮胎动力学试验能力。由于轮胎动力学试验的复杂性和先进性，技术往往严格保密。国内个别高校和研究机构在该领域开展了较深入的研究，建立了轮胎动力学试验和建模能力，如吉林大学、中汽研等。一些国内轮胎生产公司也逐步引入相关试验设备，但试验能力和数据处理方面经验相对不足。国外相关研究开展较早，工程经验相对成熟，如德国的FKA和北美的MTS等。

3.1 轮胎动态试验台架

在郭孔辉院士带领下，吉林大学开发的平板式轮胎动态特性试验台，如图2所示：

该轮胎力学特性试验台主要由四个系统构成，即计算机主控制系统，液压伺服系统，机械运动系统和信号采集系统，其性能技术指标如表示：

北美的MTS轮胎动态力学特性试验台，如图3所示，其性能技术指标如表2所示。

3.2 轮胎动态测试试验

本文以某ADVANCE 305/80R20轮胎为试验对象，进行纯侧偏、纯纵滑、纯侧倾、动态垂直刚度、轮胎有效滚动半径、复合侧偏侧倾、复合侧偏纵滑试验的力学特性测试及数据处理。

3.2.1 轮胎稳态侧偏力学特性试验

试验工况描述：

l）轮胎垂直载荷（N）： 3920、7840、14700、16660、18130、19600

2）轮胎胎压（KPa）：450

3）轮胎侧偏角（Degree）：0、±0.5、±l、±1 5、±2、±4、±6、±8、±10

试验结果见图4和图5所示：

3.2.2轮胎稳态侧倾力学特性试验

试验工况描述：

1）轮胎垂直载荷（N）： 14700、16660、18130、19600

2）轮胎胎压（KPa）：450

3）轮胎侧偏角（Degree）：0、±2、±4、±6、±8、±10

试验结果见图6图7所示：

3.2.3 轮胎稳态纵滑力学特性试验

试验工况描述：

1）轮胎垂直载荷（N）：14700、16660、18130、19600

2）轮胎胎压（KPa）：450

3）制动滑移率（一）：按设备能力做至最大试验结果见图8所示：

3.2.4 轮胎复合侧倾侧偏试验

试验工况描述：

1）轮胎垂直载荷（N）：14700、16660、18130、19600

2）轮胎胎压（KPa）：450

3）轮胎侧倾角（Deg）：6、--6

4）轮胎侧偏角（Degree）：0、±0.5、±1、±1.5、±2、±4、±6、±8、±10

侧倾角为6deg时，试验结果见图9和图10所示：

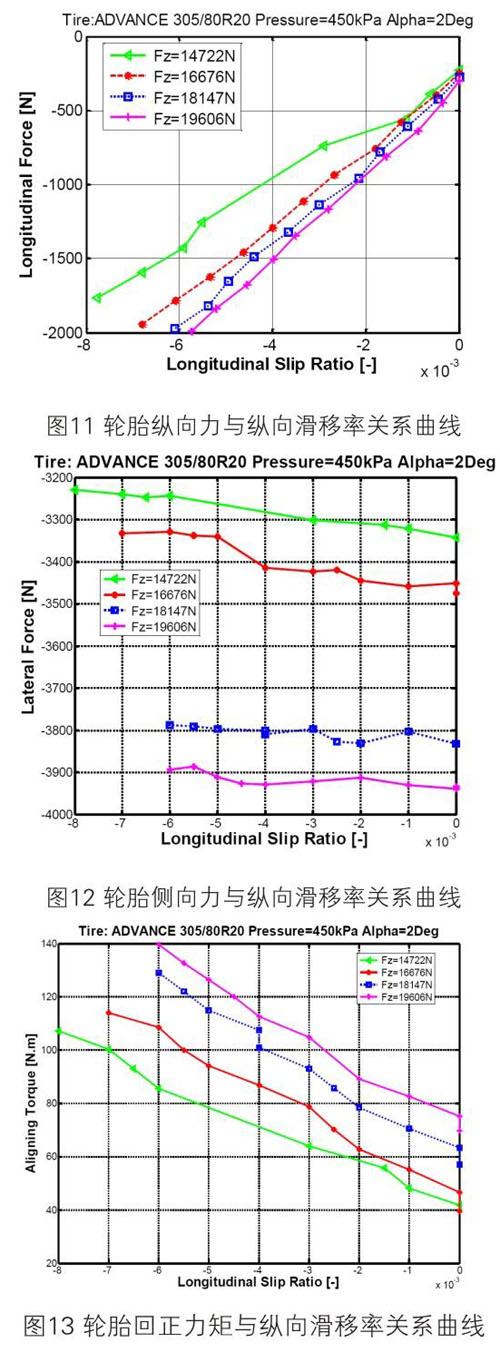
3.2.5 轮胎复合侧偏纵滑试验

试验工况描述：

1）轮胎垂直载荷（N）：14700、16660、18130、19600

2）轮胎胎压（KPa）：450

3）轮胎侧偏角（Degree）：2、4

侧偏角为2deg时，结果见图11、图12和图13所示。

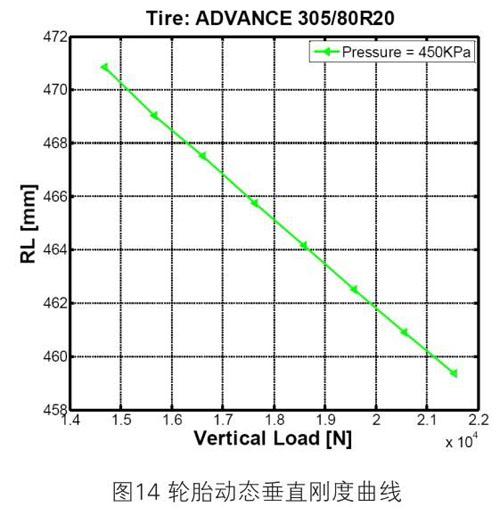
3.2.6 轮胎动态径向刚度试验

试验工况描述：

1）轮胎垂直载荷（N）：14700、15680、16660、17640、18620、19600、20580、21560

2）轮胎胎压（KPa）：450

试验结果见图14所示：

3.2.7 轮胎有效滚动半径试验

试验工况描述：

1）轮胎垂直载荷（N）：14700、15680、16660、17640、18620、19600、20580、21560

2）輪胎胎压（KPa）：450

试验结果见图15所示：

4 轮胎动力学模型的建立

4.1 轮胎模型建立过程

根据轮胎动态试验所得试验数据，建立轮胎模型的主要过程，如图16所示：

1）参数辨识：如前文介绍，Magic Formula轮胎模型是由一套数学公式来描述轮胎的力学特性，通过对大量的轮胎力特性的试验数据进行回归分析，将轮胎力特性通过含有拟合参数的公式有效地表达出来。轮胎模型各工况包含大量的参数因子，通常通过数据专业的数据处理软件，将各工况下的参数因子辨识出来;

2）模型构建：由于Magic.Formula轮胎模型在行业的广泛应用，其模型已形成标准的参数格式文件，只需将上一步辨识得到的各参数因子，按照正常的位置填人轮胎模型文件即可;

3）试验对标：在专业分析软件中建立虚拟轮胎试验台，开展相应的测试T况的仿真，将仿真结果与测试试验结果比较，已达到模型精度验证的目的。

其中，参数辨识过程最为重要，难度最大。由于过程复杂，通常需要具备一定的辨识经验。

4.2 轮胎模型参数辨识

Magic Formula轮胎模型主要包含以下三组特性参数^[4]，如图17所示：

1）力和力矩特性参数：纯纵滑、纯侧偏和复合工况下的轮胎稳态响应，图17中绿色部分;

2）轮胎基本属性参数：轮胎垂直刚度、轮胎有效滚动半径、轮胎接地印记长度宽度、松弛长度等，图17中浅蓝色部分;

3）轮胎包容特性和轮胎带束特性参数，图17中红色部分。（高版本轮胎模型需求）参数辨识的基本思想，如图18所示：

1）将试验数据的一部分作为输入（如垂直载荷、侧偏角、侧倾角、纵向滑移率、标称载荷、自由半径等），给定模型参数一组初值，根据轮胎模型公式，计算出输出量（如纵向力、侧向力、回正力矩等），然后求出模型输出变量与试验测试值之差的平方和;

2）若求出的值小于一个很小的量（用户设定的值），则认为这组模型参数值可以很好的表达出试验数据的，停止迭代，输出这组模型参数值作为参数辨识的结果值;

3）若求出的值不小于这一小量，则在模型参数初始值基础上修改模型参数，重复上一步骤，直到仿真值与试验值之差的平方和小于设定的小量，停止迭代，将最后一组模型参数值输出，作为参数辨识的结果值。

通常采用专业辨识软件工具开展数据回归，拟合出各工况下的轮胎参数因子，需要设置各待拟合参数的初始值，上下边界值，拟合步数等。残留标准差按下式计算。

由于轮胎模型的工况较多，每个工况待辨识的参数很多，这里不一一列举，仅以纯纵滑工况下的纵向力参数辨识为例，如图19所示：

轮胎纯纵滑工况纵向力随纵向滑移率变化特性参数辨识结果如表3所示：

4.3轮胎模型的精度验证

在ADAMS/Car中，集成了一个评估单个轮胎在各种激励和其它条件下特性的试验台Testrig，如图20所示。轮胎试验台是一个独立的，不依附于整车或子系统的模型工具。轮胎试验台在某种程度上可以说是轮胎属性文件的图形化工具^[3]。

虚拟的轮胎试验台中包含有一个包含轮胎的车轮，车轮安装在心轴上并通过弹簧、预加载的大作用力、同定高度心轴与试验台的平台路面接触。

虚拟轮胎试验台可以模拟轮胎实际动态测试试验的相关工况。平台上的路面可以是同定或运动，路面自身形态可以是平坦或有凸块（凹坑）或通过属性文件自定义，轮胎的运动可以增加转角（轮胎侧偏变量），轮胎自转（纵向滑移变量），相对路面的倾角（侧倾角），轮胎中心的垂直和纵向位移，初始轮胎的回转速度和纵向速度可用轮胎属性文件中的轮胎自由半径计算。

将建成的轮胎属性文件在虚拟轮胎试验台上开展响应工况的仿真，将仿真结果与试验结果对标，可实现轮胎模型的精度验证。以纯纵滑工况下的纵向力试验对标为例，如图21所示：

5 轮胎模型的应用

为验证轮胎模型在整车动力学仿真中的合理性，利用ADAMS进行整车操纵稳定性仿真。车辆模型的参数均为实际测得，轮胎模型是通过完成轮胎力学特性测试、参数辨识建立的Magic Formula轮胎模型。本文列举了有代表性的开环角脉冲及闭环蛇形工况，并与整车试验结果进行了对比，具体工况定义及仿真结果如下所示。

1）角脈冲工况

车速为80km/h，试验时的方向盘转角如图22所示，车辆的横摆角速度仿真及试验曲线如图23所示：

2）蛇形工况

车速为30km/h，蛇形试验为闭环试验，本文为验证所建立轮胎模型的精度，将实际的方向盘转角作为输入，如图24所示。车辆的侧向加速度仿真及试验曲线如图25所示：

图25 蛇行仿真车身质心侧向加速度结果曲线

从以上整车角脉冲及蛇形工况的仿真及试验数据对比可以看出，所建立的Magic Formula轮胎模型能很好地仿真车辆的操纵稳定性，并具有较高精度。

6 总结

本文首先介绍了Magic Formula轮胎模型的理论基础，其次介绍了国内外具有代表性的轮胎动力学特性的试验台架，并结合一款具体轮胎介绍了主要轮胎测试工况;根据Magic Formula轮胎模型的建模方法，结合轮胎模型参数辨识和轮胎模型精度验证等手段，建立了Magic Formula轮胎模型。最后，将建立的轮胎模型进行了整车操纵稳定性典型工况下的仿真分析，通过与试验数据的比较，验证了所建轮胎模型的合理性和精度。

通过在轮胎动力学试验与建模技术方面的研究工作，掌握了建立轮胎模型的一般方法和主要流程，对Magic Formula轮胎模型有了较为深入的理解。然而，由于轮胎动力学学科本身的技术复杂性，以及缺少轮胎测试台架等条件，对轮胎模型的研究还比较有限，进一步工作主要针对适用于平顺性、耐久性分析的高频轮胎模型开展研究，以拓展车辆动力学中轮胎模型的应用领域，提升车辆性能仿真的精度。

参考文献：

[1]郭孔辉汽车操纵动力学[M].长春：吉林科学技术出版社.1991.

[2]郭孔辉，管欣汽车性能设计技术的进展[J].中国机械工程，1997，8（1）94-96.

[3]卢荡轮胎动态侧偏特性建模及对汽车操纵稳定性的的影响[D].长春：吉林大学汽车工程学院2003.

[4]ADAMS 2017 help. Tire Models. Using the PAC2002 Tire Model. Basics of the Magic Formula in PAC2002.

[5]ADAMS 2017 help. Adams Tire Tools. Tire TestRig.