数学支架式教学中支架的类型

陈晨

【摘要】支架式教学模式突出了学生在学习中的主体地位，有利于培养学生的自主探究能力.进行支架式教学关键点就在于“支架”，“支架”按照性质来分，可以分为认知支架和情感支架.

【关键词】数学；支架式教学；支架的类型

支架式教学源于苏联著名心理学家维果茨基提出的“最近发展区”理论.支架式教学就是教师在学生的最近发展区内提供支架，帮助学生跨越最近发展区.其中，“支架”的原意是指建筑行业中使用的“脚手架”，这里用来比喻对学生解决问题和建构意义起辅助作用的概念框架.在支架式教学模式中，最重要的问题是弄清楚支架的类型有哪些，只有弄清楚有哪些支架，才可以依照不同支架的特点选择适合教学内容的相应支架.支架的类型多种多样，我们按支架的性质来分，可分为认知支架和情感支架.

一、认知支架

认知支架指的是学生在认知过程中教师提供的概念框架.按照不同的形式，认知支架可以分为以下几类：问题类、实物类和情境类.

（一）问题类认知支架

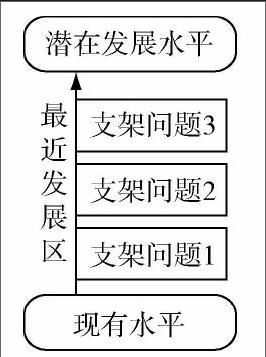
问题类认知支架就是将所要学的新理论知识隐含在一个或几个支架问题中，然后再将支架问题分解为若干子问题，学生通过对这些问题进行分析、讨论，得到讨论结果，然后再由教师进行综合、归纳，最后得出问题的正确答案，达到潜在的发展水平.

过程如图所示.

例如，在学习n边形的内角和时，学生现有的水平是知道三角形的内角和为180°，潜在发展水平是掌握n边形内角和公式.教师可首先提出问题一：四边形的内角和是多少？怎么得来的？学生通过思考讨论可能会得到可以将四边形分成两个三角形.教师可再提出问题二：五边形的内角和是多少？经过这两个问题的铺垫，学生可能会联想到可以将n边形分成若干个三角形.紧接着教师提出问题三：n边形可以分成多少个三角形？学生得出正确答案之后，教师就可以提出最后一个问题：n边形的内角和是多少？即到达了潜在发展水平.

（二）实物类认知支架

实物类认知支架就是教师借助实物演示数学中抽象的情境概念框架.实物类支架不但包括直观教具，也包括计算机课件.实物类支架的作用主要是直观性很强，学生能够尽快直接的学到教师所教内容.同时，运用实物类支架也能够吸引学生的注意，激发学生的好奇心，提高学生的学习兴趣，同时也增加了课堂的趣味性.

实物类认知支架最简单的例子就是小学数学课堂上教师为了让学生学会数数，使用手指、糖果、火柴棒等实物让其和抽象的数字建立联系，等学生掌握之后，再撤去这些实物.通过实物进行演示，教师将课堂还给学生，让学生自主探索，教师所要做的就是在学生停止不前的时候给予提示.在运用实物类支架时教师要注意所用实物要适当，否则不但不会帮助学生理解还会困扰学生，同时，实物演示也不可太过复杂.在条件允许的情况下，应鼓励学生自己动手操作.

（三）情境类支架

情境类支架就是教师将抽象的数学问题寓于具体情境中提供的概念框架.创设的情境多种多样，总的来说有创设游戏情境，创设实际情境，创设现实情境，创设过程展示情境，创设悬念情境，创设竞赛情境，创设类别、猜想情境，创设争论性情境，创设动态情境等.

设置情境性支架能够创造轻松的课堂氛围，吸引学生学习兴趣，激发学生学习动机，对知识的学习有促进作用.例如，独立事件同时发生的概率的教授.在课开始前，教师可设置这样的一个情境：俗话说：“三个臭皮匠顶上一个诸葛亮”，能顶得上吗？比如，在一次有关“三国演义”的知识竞赛中，三个臭皮匠能答对题目的概率分别是50%，45%，40%，诸葛亮答对题目的概率为80%，如果将三个臭皮匠组成一组与诸葛亮比赛，各位选手独立解题，不得商量，团队中只要有一人解出即为获胜，答对题目多者为胜方，问哪方胜？在这样直观生动情境下，既激发了学生学习的兴趣，引起学生的认知冲突，又能促进学生对独立事件概念的理解，同时又把原来冷冰冰的数学知识变成了生动有趣的感性材料，使枯燥的数学知识变成了富有人文气息的数学关怀，能够让教学取得良好的教学效果.

二、情感支架

德国教育学家第斯多惠说：“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞”.有效的情感支架对于学生的学习过程具有明显的推动能力，因此，教师应采取各种手段去创设情感情境，让学生以饱满的热情参与到学习当中去.例如，在讲解等差数列求和公式这一新知识时，可以将德国大数学家高斯10岁那年聪明解答“1+2+3+…+100=？”的故事以及其他数学家对等差数列的研究和发展做出的贡献介绍给学生，学生聚精会神了解这些知识，会不自觉被数学家那种大胆探索，不断开拓的精神所感染，从而加强情感教育，激发学生学习数学的自觉性和积极性.然后再给出下面的问题：在一个堆放铅笔的V形架的最下面一层放一支铅笔，往上每一层都比它下层多放一支，最上面一层放100支铅笔，问这个V形架上共放多少支铅笔？学生通过教师的启发，很快便会得到下面的结果：1+2+3+…+99+100=50×101=5 050，进而构建出等差数列前n项和公式.

综上所述，支架式教学的支架的类型各不相同，各有各的长处和弊端.无论在教学中采用何种方式的支架，都要考虑学生的“最近发展区”，只有这样搭建的支架，才能让学生通过支架去构建数学知识的大厦，也才会逐步使学生学会自己去设计支架，掌握学習数学的好方法，培养进一步学习的能力.

【参考文献】

[1]杜军.“支架式”教学应重视“脚手架”的搭建[J].教育理论与实践，2005（7）：51.

[2]洪树兰.数学“支架式教学”[D].昆明：云南师范大学，2005：33-34.

[3]黄晓华.初中数学支架式教学的主要类型及特征[J].数学教学通讯，2004（4）：33-34.