数形结合在解决函数问题中的应用

胡光启

【摘要】数形结合是对于客观事物的抽象性反映，数学学习过程中处处渗透着数形结合的思想.数与形问题的解决，是为了培养学生们的思维和判断能力，并且构成合理的数学教学任务.本文通过对于函数图像和几何图形的了解，结合实际教材的情况，分析数形结合在现实问题中的使用的意义和作用.

【关键词】数形结合；抽象性；函数

函数的图像和性质是对于数学问题解决的突破口，函數的图像是数学函数解析式的直观反应.通过图像的形式可以了解函数和变量之间的关系，函数的图像代表着函数的性质.中学阶段函数的理论对于数与形的解读具有很重要的作用.函数的分析，既可以帮助数形结合问题的数据分析，同时也可以帮助解决应用的问题.数形结合的理论和思想是形成数与形之间对应关系重要，通过对数与形之间的相互关系的转化，来解决数学问题的思考.就目前的数学教材来说，如何才能更好地加强对于数与形在数学学习中的应用，就需要通过大量的实证，了解函数题解答过程中的研究和分析.

一、数形结合思想的基本理念

数和形在数学研究过程中具有重要的作用，数形的研究，不仅仅是对于物体数量分析的研究，更重要的是为了研究物体的形状的计算.数形结合的思想就是将物体的数量、精确程度和物体形状的直观性不断结合在一起.数形结合将抽象的数学语言，通过直观性的图形不断的转换加以表达，帮助人们把抽象的思维和形象联系在一起.数形结合的方式不仅仅说明了数量之间的关系，而且还可以将复杂的问题变得更加简单.数形结合是解答日常问题的重要方法，数形结合的思维是需要将数学中与之对应的基本对象和关系进行很好的考查和结合.数形结合的思想可以通过充分发挥代数和几何学科的理论，来解决代数方程中的问题.数学的结合思想形成了数学的思想.通常情况下我们可以将数形的发展，变成数学发展中和谐性的统一.

二、数形结合思想在数学学习过程中的地位和作用

数形结合是通过数量的形状和图像的性质来加以转化的，数形结合的方式可以将抽象的思维和形象的思维，不断结合在一起.让抽象的数量和直观的图形结合在一起来研究数量的抽象性质，因此，数形结合是几何和代数之间的解决问题的方式.

（一）数形结合在数学中的作用

数形结合是培养学生分析数学问题和解决数学问题的基础，数形结合的理念贯穿于数学发展之中.数形几何是中学数学学习过程中的一种基本理念，数形结合可以通过运用人们常用一些思维，将所有的数学问题都加以解决.最主要的数形结合更具有直观性和生动性，对于数学问题的解答更具有规范性和严谨性.

（二）数形结合在数学学习过程中的价值

数形结合的主要方式是将数量的关系和图形之间不断地变化，数形结合是数学信息的转换.数量的抽象性质说明了数据的形象美，而图像的性质说明了数量的表现，是数形结合的方式.数形结合通常情况下是需要来研究曲线和方程的对应关系，实数和数轴上的点的对应关系.数形结合也是研究函数的发展关系以及代数式和等式的发展关系.

（三）数形结合在数学学习中的运用

数形结合在一定程度上使用的范围较广，在数学问题解答的过程中，解答区域定义域和值域，都需要运用到数形结合的思想.数形结合不仅仅可以方便解题的思路，同时还可以避免存在更加复杂或者是无用的计算，让学习数学过程中的计算问题加以解决.

（四）数学数形结合的思想可以更快地解答函数题中的问题

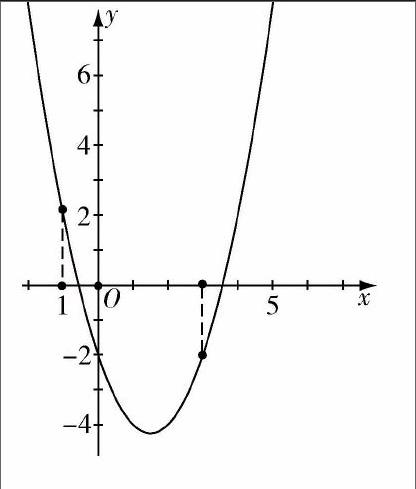
数形结合的方式，可以方便对于函数的图像、函数的性质以及函数理论问题的解决.有助于应用函数的性质分析和解决问题的分析.比如，在研究函数的值域求解方面，我们就可以发现数形结合的应用有重要的作用，如右图所示：

借助图像可知道，该函数的值域为-174，2.

由图我们可以知道，在数学学习过程中常见问题就是对于函数的求解问题，数形结合的思想可以更好地通过图像让我们了解出函数的值域分析，并在区间内解决函数的值域问题.

三、结束语

数形结合的思想是数学问题思考的一种模式，数形结合是解决数学问题的主要主线.数形结合的思想，让复杂的问题变得更加简单化.数形结合可以把抽象的数据变得更加直观.数形结合将几何图形不断结合在一起，加强对于数学事物的本质把握和规律的总结，数形结合的思想具有灵活性和创造性.在实际生活中函数运用过程，需要通过多方位、多角度的思考来选择合适的分析路径.要想学好函数就需要掌握丰厚的基础知识和熟练的技术技巧，数形结合是数学学习过程中的重要一部分，在数学学习思想中，涉及的环节很多，因此，要想加强对于数学的学习能力，首先需要提高思维认识和创新能力.

【参考文献】

[1]赵发源.九年义务教育初中数学教材中的数学思想和方法[J].甘肃教育，1995（Z1）：73-74.

[2]孟灵芬.数形结合思想在初中数学中的地位和作用[J].教育艺术，2008（2）：77.

[3]岑惠燕.数形结合思想的教学意义[J].新课程（综合版），2011（10）：87-88.

[4]吴方淼.运用数形结合思想解题的常用策略[J].中学教学参考，2009（5）：67-68.

[5]王林全，吴友昌.初等数学解题研究：第2版[M].北京：科学出版社，2009.

[6]汤服成.中学数学解题思想方法[M].桂林：广西师范大学出版社，2005.