基于点云数据算法的高程校准模型

(长江水利委员会 长江中游水文水资源勘测局，湖北 武汉 430010)

1 研究背景

在洪水风险图绘制、涉河工程设计洪水计算、山洪灾害分析评价等工作中，均需要获得准确的地形高程数据，但实际往往难以实现。例如，长距离油气管道工程可能需要穿越河流，而很多河流只有小比例尺的地形资料和少量岸上地形数据，缺乏穿越断面实测水下地形或断面高程数据，给穿越断面的水位流量关系计算分析造成了不利影响；在洪水风险调查工作中一般仅进行沟道断面测量和宅基地测量，很少开展地形测绘工作，测点数据无法保证洪水淹没线(等高线)的准确勾绘，给风险等级评价及风险图的准确绘制造成影响。为了解决上述问题，在现有的少量地形或高程成果数据基础上，通过技术手段对其进行补充完善十分必要。

GoogleEarth软件可提供全球任意区域的公开高程数据，但其平面坐标系统及高程基准和实际应用的不同，而且精度较低，尤其是绝对高程数据。本文通过相关算法，利用测区已有的少量测量数据关联GoogleEarth的海量高程数据，进一步推求区内任意点的高程，并在此基础上建立测区数字地面模型。

2 点云校正算法

通过七参数转换模型可获取GoogleEarth的平面坐标系统和实地坐标系统间的关系；通过相关下载工具(如91卫图助手)等可获取GoogleEarth的海量高程数据，因此，关于其平面坐标转换和高程数据获取问题本文不做赘述。但需说明，GoogleEarth获取的海量高程数据并非实际测量中用到的正常高，需要进一步转换。一般情况下，任意点的Google-Earth高程与正常高之间的高程转换关系可用以下公式表示：

ζ=H-Hr

(1)

式中，H为GoogleEarth高程;Hr为正常高;ζ为GoogleEarth高程和正常高差值。

在测区选取同时具备GoogleEarth高程和正常高的测点, 利用二者的差值，根据高程差值与平面坐标的关系，用最小二乘法求出其高程转换模型，再内插出测区任意点的高程差值, 从而推求出任意点的正常高。

针对目前高程拟合的研究现状，通过两种拟合方法的高程转换模型即空间曲面函数法和数学曲面逼近法，实现对GoogleEarth点云数据的校正[1-5]。

2.1 空间曲面函数法

当测区已知点布设成一定区域面时，可以用空间曲面函数法求定任意点的正常高。假设测量区域内任意点的坐标为P(x，y)，GoogleEarth高程和正常高差值为ζ(x，y)，则其空间曲面函数为

(2)

式中，ai为待定参数，当测区已知点数量不小于参数个数时，可推求出参数ai，进一步求出测区任意点的GoogleEarth高程和正常高差值。

根据测区情况的不同，可选择不同的参数转换函数进行拟合。基于测区区域面大小，空间曲面函数法可概括为平面函数法和曲面函数法。

2.1.1 平面函数法

平面函数法即为线性内插，在小范围区域内(本文一般为2 km以内)，可以认为GoogleEarth和正常高的起算面趋近于平面。此时，GoogleEarth高程和正常高的函数关系为

ζ(x，y)=ao+a1x+a2y

(3)

式中，ai(i=0,1,2)为未知参数，已知点的数量不少于3个。

四参数曲面函数和平面函数法类似，选用公式(2)的前3项和第5项进行拟合，函数曲面的表达式为

ζ(x，y)=ao+a1x+a2y+a3xy

(4)

式中，ai(i=0,1,2,3)为未知参数，已知点数量至少4个。

2.1.2 曲面函数法

当测区范围较大时(本文一般为2 km以上)，为获得高精度的转换结果，应尽可能多的利用测区已有控制成果，求出相应的空间曲面函数。本文以6个未知函数参数为例，其曲面函数的数学模型可以表示为

ζ(x，y)=a0+a1x+a2y+a3x2+

a4xy+a5y2

(5)

若已知测区内高程差值点的个数不小于6个，则可根据最小二乘法VTPV=min求出以上未知参数ai(i=0,1,2，…，5)，由此根据公式(5)可推求出测区任意点的高程差值，再根据公式(1)即可求得任意点的正常高。

2.2 数学曲面逼近法

本文建立数学模型，用多个曲面高度逼近测量区域的高程差值，然后根据GoogleEarth高程来计算常规基准下的正常高。建立任意点和所有已知点函数关系，将这些函数的值迭加起来，获取最佳的曲面拟合结果。根据上述思路，假设测区内任意点的坐标为P(x，y)，其高程差值为ζ(x，y)，则其数学曲面逼近法的数学模型为

(6)

式中，aj为未知参数，Q(x,y,xj,yj)为x和y的二次核函数，其中核心在(xj,yj)处，ζ可由二次式的和确定，故称多面函数；(x，y)为高程差值待求点的坐标，(xj，yj)为高程差值已知的点的坐标。核函数一般可取[2-5]：

Q(x,y,xj,yj)=(x-xj)2+(y-yj)2+δk

(7)

式中，δ为光滑因子，k取值一般为1/2，-1/2，3/2。分别对应于以下3种类型：

正双曲面型：

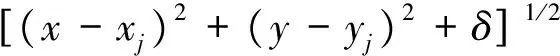
(8)

δ当其值为0时，正双曲面退化为圆锥面。

倒双曲面型：

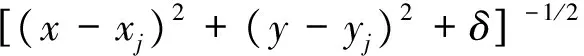
(9)

三次曲面型：

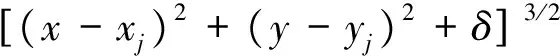
(10)

式(6)可表示为

ζ=Qa

(11)

未知参数a可根据已测点的垂直速率值按最小二乘法计算得到：

a=(QTQ)-1QTζ

(12)

于是任意点p的高程差值可求得：

ζp=Qpa=Qp(QTQ)-1QTV

(13)

再根据公式(1)便可求得任意点的正常高。

2.3 实例分析

本文以山洪灾害调查工作中的一个沿河村落作为研究对象，研究区域内布设有4个控制点(G1～G4)、3个控制断面以及相关的宅基地测量点，分布情况见图1。

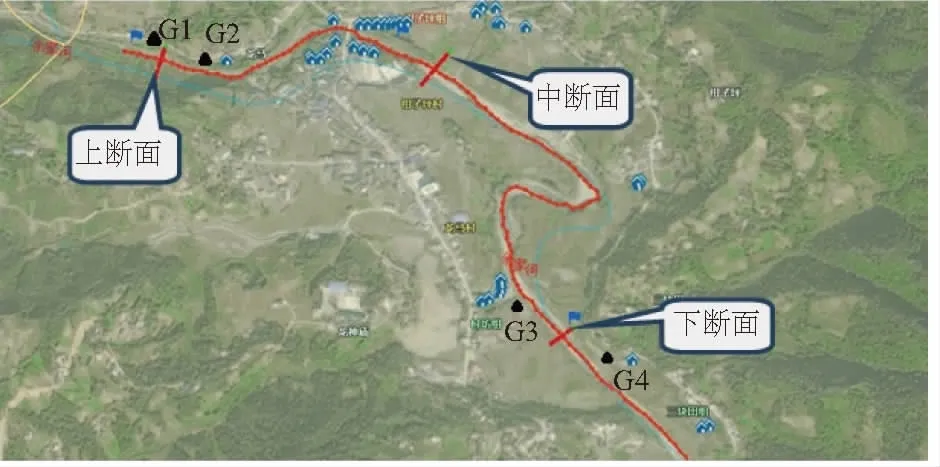
图1 测区点位分布

由于研究区域河道长度大于2 km，本文分别采用曲面函数法和数学曲面逼近法进行高程模型的转换，并在此基础上进行精度分析。

(1) 沿河村落主要从4个控制点和3个断面中选取已知点，4个控制点参与计算；选择地势平坦、测量精度较高的3个已知点参与计算，通过平面坐标基准转换在GoogleEarth中读取相应位置的GoogleEarth高程，从而完成7组同时具备Google-Earth高程和实测正常高程已知点的选择。

(2) 分别通过曲面函数法和数学曲面逼近法计算7组已知点，求解未知参数，得到相应的高程转换模型。

(3) 将已测量过的断面和宅基地点分别代入2种高程转换模型，得到其对应的正常高，利用所得的2种正常高与测量已知高程对比，来验证两种转换模型的转换精度，其精度对比如表1。

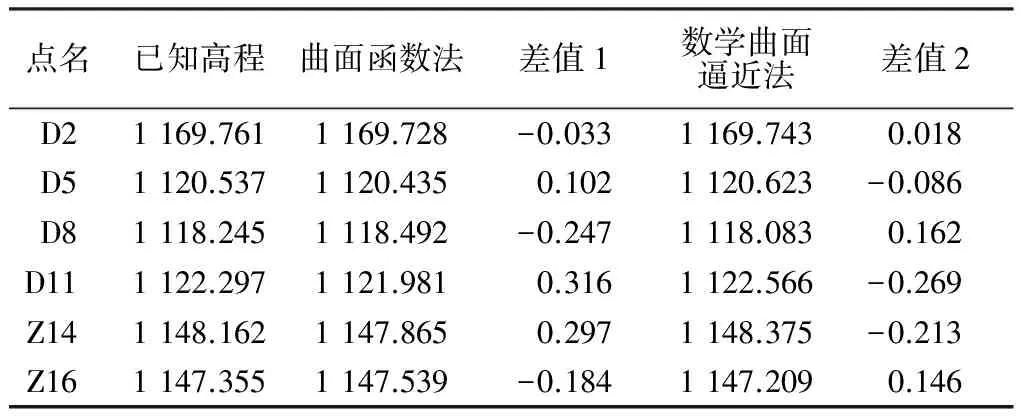
表1 部分测点两种方法精度对比 m

从表1可以看出，两种转换模型都能满足山洪灾害调查测量的精度要求。总体而言，数学曲面逼近法的精度比曲面函数法的精度略高。其不足之处在于，对于地势高差较大或者高程变化急剧时，曲面函数法精度损失较为严重；对于数学曲面逼近法，其核函数的选取，以及平滑因子都会对精度产生较大影响，要多次尝试。

3 数字地面模型的建立

通过GoogleEarth点云数据校准实现了测区任意点的GoogleEarth高到正常高的改算，批量获取研究区域内GoogleEarth点云的正常高；再利用MapGIS软件调入点云数据，基于点云高程数据建立三角网和初设数字地面模型，并通过图像分析系统把下载好的卫星影像转换为MSI格式，再利用MSI文件装入纹理文件可完成基于GoogleEarth的数字地面模型的建立，见图2。

图2 数字地面模型示意

4 结 语

本文提出了用空间曲面函数法和数学曲面逼近法两种点云校正算法来实现从GoogleEarth高程到正常高的转换。结合实例比较分析表明，空间曲面函数法和数学曲面逼近法都可满足实际生产中的应用，但也存在其相应的局限性，实际生产中应根据测区的自然条件和已知点的分布等情况选择合适的转换模型；在GoogleEarth点云数据校正后可利用MapGIS软件建立数字地面模型，实现测区高程可视化，为山洪灾害调查评价或其他行业服务。

[1] 雷伟伟，郑红晓.二次曲面拟合法在区域似大地水准面精化中的应用[J].测绘与空间地理信息，2008，31(6)：38-42.

[2] 江在森.中国西部大地形变监测与地震预测[M].北京：地震出版社，2001.

[3] 刘万林，王利，赵超英.GPS水准的有限元法与多面函数法的加权综合模型[J].地球科学与环境学报，2004，26(3)：49-51.

[4] 张菊清，刘平芝.抗差趋势面与正交多面函数结合拟合DEM数据[J].测绘学报，2008，37(4)：527-530.

[5] 黄立人，陶本藻，赵承坤.多面函数拟合在地壳垂直运动研究中的应用[J].测绘学报，2003，22(1)：25-31.