基于物理层安全特征的不可信中继行为预测

付晓梅, 陈 莉, 常 帅

(1. 天津大学海洋科学与技术学院, 天津 300072; 2. 天津大学电气自动化与信息工程学院, 天津 300072)

0 引 言

传统的信息传输安全性是通过密钥加密技术实现的[1]。随着计算能力的不断提高,依赖于密钥复杂度的密钥加密技术的安全性受到挑战。 物理层安全技术从另外一个思路,即利用无线信道的衰落特性来防止窃听者获取传输信息[2-3],实现安全传输。其基本思想是利用无线信道衰落特性,使窃听信道条件差于合法信道条件,从而实现安全传输。但是,当源节点与目的节点之间的合法信道条件差于源节点与窃听节点之间的窃听信道条件时,安全传输将难以保障。近年来,协作通信通过中继节点协作转发接收到的信号或协作干扰窃听节点[4-6]可以打破上述信道条件限制,通过提高合法信道条件或降低窃听信道条件,从而实现安全传输,成为研究热点。

然而,在实际应用中,节点在分布式环境下,由于节点自身能量制约或被恶意节点控制,节点行为不仅有协作行为,还存在自私、恶意阻塞等行为的可能。这些不可信行为使系统的安全性能受到很大影响。文献[7-8]研究了中继节点的自私行为对物理层安全性的影响,自私行为会降低安全性;文献[9-11]研究了中继节点的恶意阻塞行为对物理层安全性的影响,恶意阻塞使安全的系统不再安全。上述研究表明中继节点表现出的自私、恶意阻塞等不可信行为对系统的安全性影响很大,所以建立中继行为模型以对不可信行为进行检测是保障安全性传输的前提。

博弈理论是研究具有斗争或竞争性质现象的数学理论和方法。博弈论考虑游戏中个体的预测行为和实际行为,并研究它们的优化策略。博弈分为静态博弈和动态博弈,动态博弈指双方的行动有先后顺序并且后行动者可以知道先行动者的策略。将博弈理论应用于物理层安全性研究是近年来的研究热点,主要应用博弈理论进行中继节点的选择[12-15],其前提是对节点的行为类型已知。本文基于随机博弈理论对节点行为类型进行预测,随机博弈是一类由一个或多个参与者进行的、具有状态转移概率的动态博弈,被应用于与状态转移相关的利益冲突的模型研究中[16-19]。

本文基于随机博弈理论,研究中继节点行为的物理层安全特征,建立中继节点的动态行为预测模型,获得中继节点产生不可信行为的概率。

主要包括以下两个部分:①建立基于随机博弈的不可信中继节点的行为预测模型,获得中继行为出现的概率;②研究基于连续时间马尔可夫链(continuous-time Markov chain, CTMC)的物理层安全特性。

1 系统模型

中继信道模型如图1所示,S为源节点,R为中继节点,可能表现出协作、自私或恶意干扰行为,E为窃听节点,D为目的节点。信道系数h:{hsd,hsr,hrd,hse}是零均值的复高斯随机变量,分别表示源节点S到目的节点D,源节点S到中继节点R,中继R到目的节点D,源节点S到窃听节点E的信道路径损耗和衰落;N:{nsd,nsr,nrd,nse}是相应信道的方差为N0的加性高斯白噪声。源节点S的传输功率为Ps,协作中继节点R的传输功率为Pr。

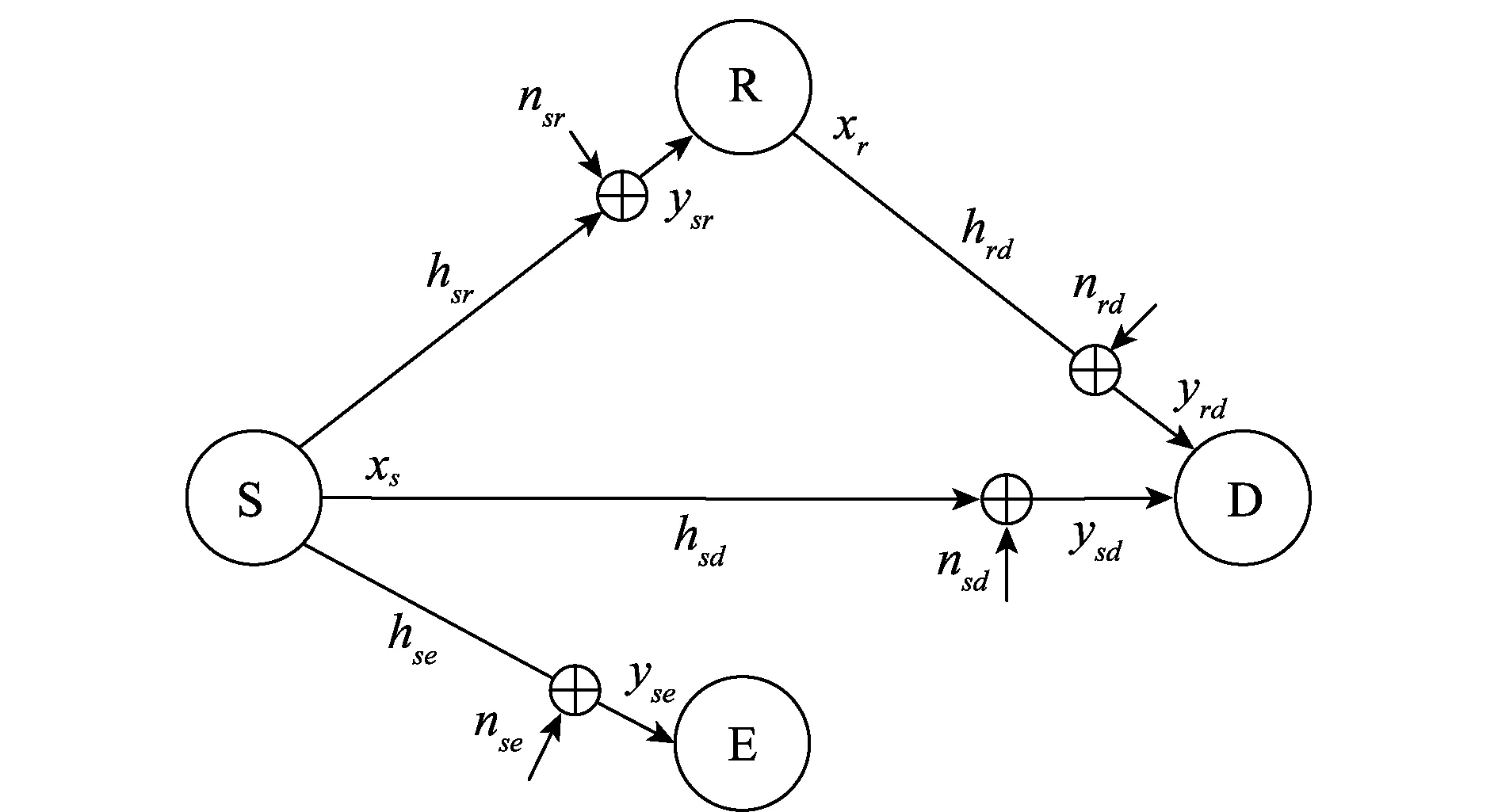
图1 中继信道模型Fig.1 Relay channel model

信息传输过程包括两个时隙,第一时隙,源节点S通过广播信道将符号信息传输到目的节点、中继节点和窃听节点,接收到的信号分别为ysd,ysr,yse:

(1)

(2)

(3)

第二时隙,协作中继节点将接收到的信号放大转发到目的节点。目的节点在第二时隙接收到的信号yrd为

(4)

令

(5)

式中,β表示中继节点R的放大增益。两个时隙接收信号进行最大比合并,则目的节点接收到的信号yrd为

(6)

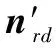
(7)

(8)

从图1的中继信道模型可以看出,源节点到目的节点的信道与中继节点到目的节点的信道为主信道M,源节点到窃听节点的信道为窃听信道W。该系统的物理层安全性能指标为安全容量[9]即为最大保密通信容量,表示为

(9)

式中,CS表示物理层安全容量;CM与CW分别为主信道与窃听信道的信道容量。

中继的不可信行为主要包括:

(1) 协作行为:放大转发接收到的信息给目的节点;

(2) 自私行为:为了节约自身的能量拒绝帮助转发信号;

(3) 恶意行为:发送干扰信息。

下面分别讨论完全协作、自私以及恶意拥塞行为下的相应的物理层安全容量的表征。

当中继完全协作时,安全容量为

(10)

当中继自私时,不向目的节点转发任何信息,即Pr=0,此时安全容量为

(11)

当中继恶意发送干扰噪声到目的节点时,此时信道噪声包括加性白噪声和干扰噪声,信道安全容量为

(12)

2 中继行为物理安全随机博弈模型

2.1 零和随机博弈

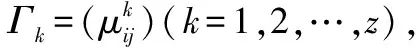
(13)

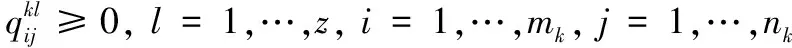
vk=val(Δk)

(14)

(15)

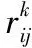
2.2 中继行为的随机博弈模型

随机博弈由一系列阶段组成。在博弈每一阶段的起始,博弈处于某种特定状态,每一参与者选择某种行动,获得取决于当前状态和所选择行动的收益。博弈发展到下一阶段,处于一个新的随机状态,这一随机状态的概率分布取决于先前状态和各位参与者选择的行动。将协作物理层安全系统可以看作是一个状态机,不可信行为的中继节点会影响系统的物理层安全性,系统则试图阻止中继节点的不可信行为,两者以目标冲突的联合行动使得系统状态发生转移,所以运用随机博弈来建立协作通信不可信中继节点的行为模型是合理的。

图2是基于CTMC建立的状态转移图,反映了不同中继节点行为对系统安全性能的影响程度。其中Gkl表示从状态k转移到状态l的马尔可夫过程,H,F,S,SM,M为博弈系统的状态。状态H和状态F分别表示中继节点行为为完全协作时的系统健康态和任意节点意外故障造成的系统失效态。S表示中继节点行为自私时的系统状态,SM表示中继节点行为是自私或恶意时系统状态,M表示中继节点行为可能为恶意时系统状态。

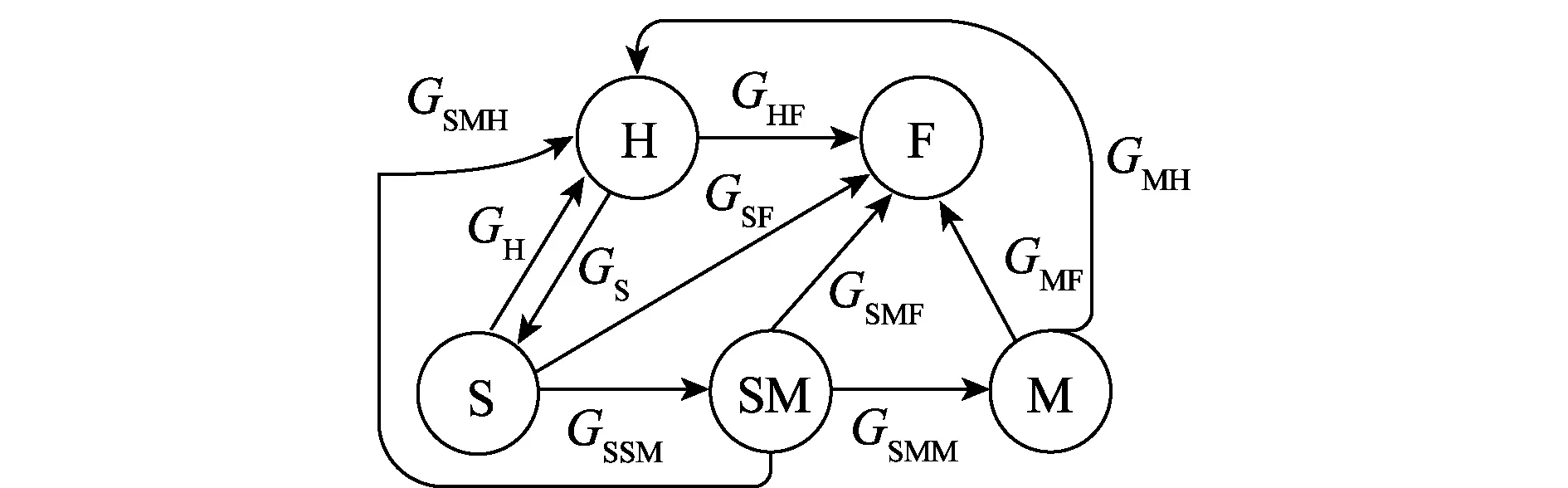
图2 状态转移图Fig.2 State transition diagram

本文重点研究中继节点行为所影响的S,SM,M状态,则博弈状态集合为Γ={ΓS,ΓSM,ΓM}。在状态ΓS时中继的行为集合{合作,自私};在状态ΓSM时中继的行为集合{合作,自私,恶意} ;在状态ΓM时中继的行为集合为{合作,恶意}。

定义两参与者零和随机博弈模型为一个五元组Ω(N,Γ,A,Q,U),设随机博弈中参与者Ⅰ为不可信行为的中继节点,参与者Ⅱ为系统,其中:

(1)N={中继节点,系统} 为参与者的集合;

(2)Γ={ΓS,ΓSM,ΓM}为博弈状态的集合,表示中继的自私行为状态、自私或恶意行为状态以及恶意行为状态。各个状态对应的是随着中继节点行为变化后,系统表现出的不同阶段状态;

被班主任误解或错怪的学生，会感到委屈、生气，担心班主任对自己有看法，影响自己进步，疑虑重重，心神不宁。

(3)A=A1×A2表示行为集合,其中A1={合作,自私,恶意}为中继节点的行为集合,A2={有惩罚,无惩罚}为系统所采取的行为集合;

(4)Q:Γ×A×Γ是随机博弈状态转移概率函数矩阵;

(5)U:Γ×A1×A2→为随机博弈收益函数矩阵。

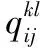
(16)

(17)

(18)

状态S与状态SM之间的转移概率、状态SM与状态M之间的转移概率为

(19)

(20)

(21)

maxαkminβkE(αk,βk)=

(22)

任意一个博弈元素val(Δk)的值都可以通过下式计算而得:

val(Δk)=E(αk*,βk*) for allΓk∈Γ

(23)

则中继节点行为的最优混合策略为

α*=(αS*,αSM*,αM*)

(24)

2.3 博弈收益

博弈模型的收益为策略组合下博弈者获得的效用,收益矩阵反应参与者的行为策略。表1给出参与者Ⅰ为中继节点,参与者Ⅱ为系统在不同行为下的随机零和博弈收益矩阵。

表1 通用收益矩阵

在无线衰落信道环境下,遍历安全容量定义为安全容量的期望,反映的是无线系统能够提供的平均安全容量大小。基于表1中的通用收益矩阵,本文采用遍历安全容量Cse作为参数衡量博弈收益。

系统的遍历安全容量为

(25)

式中,hsr,hsd,hrd为信道系数,相互独立且具有相同的概率分布。在协作系统中,系统总功率为Ptot。在两个参与者的博弈模型中,源节点和中继的初始功率分配为Ps=ξ1Ptot,Pr=ξ2Ptot(ξ1+ξ2≤1),双方行为的变化通过调节系数ξr和ξp来反映,使双方的收益产生变化,其中ξpξ1+ξrξ2≤1且ξp≥1,ξ2≥1。

从表2中的遍历安全容量收益矩阵可以看出,在中继节点选择协作且系统没有选择惩罚时,中继节点的安全容量收益为零;若系统进行惩罚,中继节点会因为选择合作行为而得到应有的奖励,此情形下,中继节点安全容量收益为正值;中继节点选择恶意行为而系统没有惩罚,则恶意使系统收益减小的值即为中继节点恶意行为时的正收益;中继节点选择恶意行为且系统对其恶意行为进行惩罚时,会采取相应行为举措,中继节点没有获得因恶意行为而产生相应的收益,其所减少的收益为中继节点得到的负收益。中继节点自私或恶意行为的情形相同,因此收益值将会影响中继的行为。

表2 遍历安全容量收益矩阵

3 仿真实验

图3和图4仿真了不同系统状态下遍历安全容量Cs作为博弈收益时,中继行为的稳定概率与ξr和ξp关系曲线变化图形。图3为状态S下中继节点选择自私行为的稳定概率,图4为状态M下中继节点选择恶意行为的稳定概率。仿真参数如下:Ptot=10-4W,Ps=Pr=10-8W,ξr=ξp=10-4,N0=10-8W。λSSM=1/3,λSMM=3,φHS=1/160,φSH=1/40,φSMH=1,φSM=3,φFM=1/24,μ=1/120。

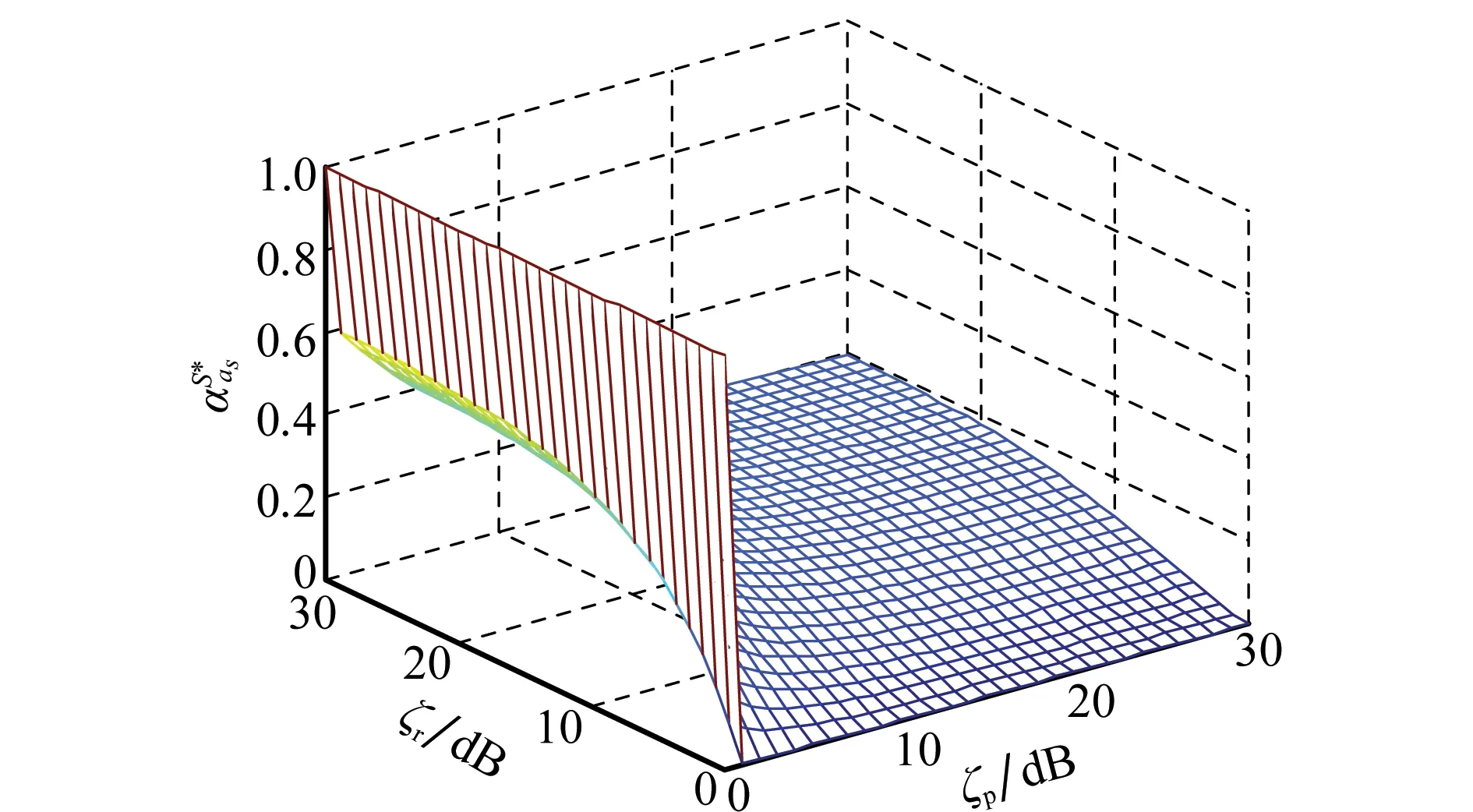
图3 中继自私行为的稳定概率Fig.3 Selfish behavior probability with ergodic secrecy

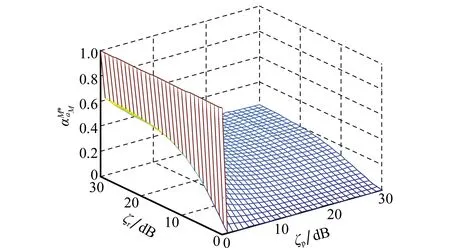
图4 中继恶意行为的稳定概率Fig.4 Malicious behavior probability with ergodic secrecy

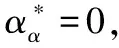
4 结束语

本文针对协作系统中中继节点行为的复杂性,基于零和随机博弈理论,利用Markov链的随机性刻画中继节点行为,捕获系统状态与中继行为之间的关系,提出了一种中继节点行为预测的方法,获得了中继节点不同行为的稳定概率,进而可以有效地进行不可信行为预测,为防御策略的选取提供依据。

[1] WYNER A D. The wire-tap channel[J]. Bell Labs Technical Journal, 1975, 54(8):1355-1387.

[2] LEUNG-YAN-CHEONG S, HELLMAN M. The Gaussian wire-tap channel[J]. IEEE Trans.on Information Theory, 2003, 24(4):451-456.

[3] CSISZAR I, KORNER J. Broadcast channels with confidential messages[J].IEEE Trans.on Information Theory,2003,24(3):339-348.

[4] WANG H M, LUO M, XIA X G, et al. Joint cooperative beamforming and jamming to secure AF relay systems with individual power constraint and no eavesdropper's CSI[J]. IEEE Signal Processing Letters, 2012, 20(1):39-42.

[5] HOANG T M, DUONG T Q, VO N S, et al. Physical layer security in cooperative energy harvesting networks with a friendly jammer[J].IEEE Wireless Communications Letters,2017,6(2):174-177.

[6] SALEM A, HAMDI K A. Improving physical layer aecurity of AF eelay networks via beam-forming and jamming[C]∥Proc.of the Vehicular Technology Conference (VTC-Fall), 2016:1-5.

[7] LÜ L, CHEN J, YANG L, et al. Improving physical layer security in untrusted relay networks: cooperative jamming and power allocation[J]. IET Communications, 2017, 11(3):393-399.

[8] WANG W, HUANG K Z, ZOU Y. Cooperation incentive mechanism for selfish users based on trust degree[C]∥Proc.of the International Conference on Information Science & Technology, 2016:204-209.

[9] HOU L J, FU X M. Physical layer security with dynamic behaviour cooperator based on coalitional game[J]. IET Communications, 2014, 8(8):1258-1264.

[10] WANG K, YUAN L, MIYAZHAKI T, et al. Strategic anti-eavesdropping game for physical layer security in wireless coo-perative networks[J]. IEEE Trans.on Vehicular Technology, 2017, PP(99):1-1.

[11] LUO G Y, LI J L, LIU Z H, et al. Physical layer security with untrusted relays in wireless cooperative networks[C]∥Proc.of the IEEE Wireless Communications and Networking Conference, 2017: 1-6.

[12] NAMVAR N, SAAD W, BAHADORI N, et al. Jamming in the internet of things: a game-theoretic perspective[C]∥Proc.of the IEEE Global Communications Conference, 2016: 1-6.

[13] FU X M, LI L, ZONG Q. Bayesian coalitional game in physical layer security[J]. Wireless Personal Communications, 2015, 85(3):1237-1250.

[14] TANG X, REN P, WANG Y, et al. Combating full-duplex active eavesdropper: a hierarchical hame perspective[J]. IEEE Trans.on Communications, 2016, 65(3): 1379-1395.

[15] HE W B, ZHANG W, BAI W, et al. Improving physical layer security in underlay D2D communication via stackelberg game based power control[C]∥Proc.of the International Conference on Computer, Information and Telecommunication Systems, 2016:1-5.

[16] WANG Y, LI J, MENG K, et al. Modeling and security analysis of enterprise network using attack-defense stochastic game petri nets[J].Security & Communication Networks,2013, 6(1):89-99.

[17] SHEN S, HAN R, GUO L, et al. Survivability evaluation towards attacked WSNs based on stochastic game and continuous-time Markov chain[J]. Applied Soft Computing, 2012, 12(5):1467-1476.

[18] LÜ J J, WANG Y, LI J Y, et al. Security analysis for web service behaviors based on hierarchical stochastic game model[J]. Chinese Journal of Electronics, 2015, 24(3):449-454.

[19] BOUCHTI A E, NAHHAL T. Cyber security modeling for SCADA systems using stochastic game nets approach[C]∥Proc.of the International Conference on Future Communication Technologies, 2016:42-47.