需求量加权的累计等待时间式多车型应急车辆路径问题研究

裴宏波，邓 烨，卢厚清

(陆军工程大学 野战工程学院， 南京 210007)

在应急车辆路径问题研究中，时效性和公平性是区别于一般车辆路径问题的显著特点。但这两者必须兼顾，如果单独强调时效性则造成物资的失衡或浪费，而一味强调公平性又会造成抢救时机的错失。因此，应急车辆路径规划的目标就是尽量提高资源利用率，即系统总成本尽量低的基础上，使时效性和公平性最优。本文将应急车辆路径问题的时效性和公平性解释如下：时效性，应急事件发生后为了及时有效控制事件发展，必须优先解决主要矛盾，具体来说，就是优先服务需求量大的点或急迫程度高的点；公平性，应急事件发生后，为避免供应时间差异过大引起社会动荡，不论需求量差异多大，每个点都应公正平等的对待，具体来说，就是不能因为优先服务“大客户”而使“小客户”等待时间太长。因此，传统成本最小化目标已不能恰当反映受灾点的真实需求[1]，考虑时效性和公平性必须重点考虑救援物资到达每个受灾点的时间[1]。学者们对此提出不同的思路：Nikolakopoulou ]等[2研究了关于以平衡车辆使用时间为目标的车辆路径问题 (BUTVRP)，该类问题的目标是在现有车辆能力下，以车辆使用时间的差最小，但当车辆使用时间的差达到最小时，各个车辆的使用时间也可能都很大。Zhang等[3]针对时间要求提出了最快完成车辆路径问题(FTVRP)，以最后一个车辆完成任务的时间最小为目标。刘霞等[4]考虑了最小最大车辆路径问题，该问题也考虑最长子线路最短，但其路径包含返回车场的路程。Ngueveu等[5]于2009年研究了累计时间式带容量约束的车辆路径问题(Cumulative Capacitated Vehicle Routing Problem，CCVRP)，提出了“累计等待时间”[5-7]这一新目标，累计等待时间等价于平均等待时间，同属于公平性的一种度量指标[8]，适合作为应急车辆路径规划的优化目标。本文在CCVRP模型的基础上进行改进，提出以“需求量加权的累计等待时间”作为优化目标，将每个应急点物资需求量差异加入模型，不仅加快运输，而且同时达到最急迫的点优先运输和整体快速运输相结合的优化效果。需求量加权的累计等待时间最短，即代表所有货物在应急运输中走的“弯路”最少，从而达到时效性最强同时兼顾公平性的目标。

在现实应急事件中，车辆类型往往不止一种，需要根据车辆的装备、容量、车龄或成本等方面不同，按客户需要或配送成本合理分配车辆路线，因此需要结合多车型车辆路径问题(Heterogeneous Fleet Vehicle Routing Problem，HVRP)进行研究。国外学者Golden等[9]最先提出多车型车辆路径问题的研究；国内学者李军、郭耀煌[10]最先研究了多车型满载车辆调度优化问题。求解算法主要是动态规划、列生成等启发式算法和禁忌搜索、遗传算法、粒子群算法、蚁群算法、量子算法等智能优化方法[11-14]。但目前多车型问题主要以降低成本、油耗、减少排量等作为优化目标，很少有将累计等待时间作为优化目标的研究，本文试图将两者进行结合，研究更加贴近实际需求量加权的累计等待时间式多车型应急车辆路径问题(Cumulative Heterogeneous Fleet Vehicle Routing Problem with demands weighting，CHVRPdw)。在现实突发事件中，由于第一时间无法得到准确的需求信息，决策者只能依据经验和历史数据进行初步预测，并根据后续信息进行动态调整。其他研究主要在于优化动态过程，本文的重点是合理规划开始阶段的车辆和路径安排，以使得未来动态调整阶段改动最少，因为需求越大的地点，发生动态变化的可能性越大，其实质是优化静态过程。其中需求量加权的累计等待时间是实现最少改动的关键指标，因为它既考虑了应急点的需求急迫程度，又考虑了优化路径的总长度。

CCVRP问题已被证明是NP-hard问题[5]，CHVRPdw是较CCVRP更为复杂的衍生模型，因此也是NP-hard问题，而对于较大规模的NP-hard问题，需要采用启发算法(heuristic algorithm)或元启发算法(meta-heuristic algorithms)解决。从现有文献资料来看，针对CHVRPdw的研究非常匮乏，对CCVRP也只有Ngueveu等人采用Memetic算法求解，而应用蚁群算法解决CHVRPdw的研究尚未见相关报道。本文采用的蚁群算法ACA(Ant Colony Algorithm)对解决路径寻优问题具有天然的优势，它是由意大利学者Dorigo M等人于1991年首先提出[15-17]。在此基础上，多种改进的蚁群算法被提出，具有代表性的有：带精英策略的蚂蚁系统[18](Ant System with elitist strategy,ASelite)；Dorigo和Gambardella(1996)提出的蚁群系统[19](Ant Colony System,ACS)；Dorigo等人在ACS基础上提出了更一般的蚁群算法Ant-Q System[16]等。其中，德国学者Stützle等[20]在1997年基于蚂蚁系统提出的改进算法——最大最小蚂蚁系统(Max-Min Ant System,MMAS)是目前蚁群优化中性能最好的算法，已成功地应用于各类组合优化问题中[21-22]，尤其是在TSP、VRP及其衍生模型上得到广泛应用。本文则是基于MMAS进行改进，通过基本CVRP算例，证明改进算法的有效性和优越性，同时结合CHVRPdw模型进行实例计算，为解决实际应急车辆路径规划问题提供新的思路。

1 CHVRPdw的数学模型

1.1 问题描述及符号说明

首先作如下假设：

1) 每个应急节点可由任何一辆车且只能由一辆车服务，每辆车完成任务后需返回车场，且车辆不得重复使用；

2) 任意两应急节点间均有路径直接到达，且整个应急运输网络为对称型网络；

3) 车辆匀速行驶，不考虑实际路况因素、装卸物资时间和返程时间；

4) 运输对象均为通用类应急保障物资，各类物资实行标准化单元运输，同时决策变量也均为整数。

问题的目标：寻找一个合适的车辆路径调度方案，在满足车辆的各类约束条件下： 1)满足各应急点的需求量； 2)所有应急节点的需求量加权累计等待时间尽量短，该目标等价于单位重量应急物资的行程时间尽量短。

1.2 数学模型

目标函数：

(1)

约束条件：

∀j∈N{0}，

∀l∈[1,2,…,Lm]， ∀m∈[1,2,…,M]

(2)

(3)

∀l∈[1,2,…,Lm]， ∀m∈[1,2,…,M]

(4)

(5)

(6)

∀m∈[1,2,…,M]

(7)

∀i∈N， ∀j∈N， ∀l∈[1,2,…,Lm]，

∀m∈[1,2,…,M]

(8)

∀m∈[1,2,…,M]

(9)

∀l∈[1,2,…,Lm]，∀m∈[1,2,…,,M]

(10)

(11)

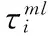
2 CHVRPdw的求解算法

2.1 求解思路

对上文建立的CHVRPdw模型进行分析，可以发现，其优化目标同传统VRP的优化目标是最短路径或最低成本有明显区别，但同开放VRP有一定相似之处，两者都忽略或不计回程时间。在用蚁群算法ACA(Ant Colony Algorithm)求解该问题时，每个蚂蚁相当于某一应急车辆，蚂蚁选择某一车型从中心车场出发，以一定的转移规则选择待访问的应急节点，当容量超过车型约束时返回中心车场，重新选择车型访问剩余节点，直到全部节点访问完毕，其中每只蚂蚁使用的车辆数必须满足车型的数量约束。然后计算每只蚂蚁所走路线的容量加权累计等待时间，值越小说明该路线越优，其留下的信息素得到增强的概率越大，反之，路径较差的子路段信息素含量随着算法迭代会逐渐降低到很小的值，而每次迭代后的蚂蚁都会倾向于选择信息素含量较大的子路段，最终会找到一条最优的车辆路径方案。蚁群算法核心是转移规则的设计和参数的优化选取，但存在很大随机性，故本文加入2-opt局部优化策略，以加快收敛速度。

2.2 算法介绍

鉴于最大最小蚂蚁系统MMAS在求解TSP、VRP等路径优化问题中的良好表现，本文拟采用MMAS算法结构来求解提出的模型。MMAS算法结构主要包括以下4个部分[23]：

1) 信息素轨迹更新

为了充分利用循环最优解和到目前为止找出的最优解，每次循环后，只有一只蚂蚁进行信息素更新，这只蚂蚁可以是当前循环中的迭代最优蚂蚁，也可以是循环开始以来的全局最优蚂蚁，MMAS中主要使用迭代最优蚂蚁进行更新：

(12)

2) 信息素轨迹限制和平滑

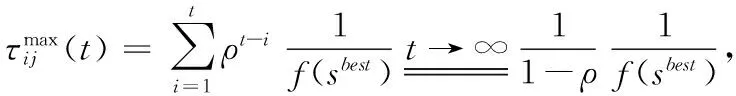
3) 信息素轨迹初始化

在第一次循环后，所有的信息素与τmax(1)相一致，如果将信息素初始化为τmin，选择概率就会增加得异常缓慢，因此，将信息素初始化为最大值τmax可以明显改善算法性能。

4) 算法收敛判析准则

有两种判断方式，达到其中之一的条件可看作收敛。① 达到一定收敛精度，Viter-Viter-1≤ΔV；② 当Maxiter=M。当然，在实验中，一般只设定迭代次数作为统一的判断准则，这样可以方便比较算法性能。

2.3 改进策略

传统的蚁群算法及其改进一般适用于求解成本最优的车辆路径问题，不完全适用于CHVRPdw的求解，必须进一步改进。

2.3.1 改进转移规则

为了扩大解的搜索空间，增加随机搜索的权重，本文以Dorigo M等提出的Ant-Q算法中的自适应伪随机比率选择规则[16]作为基础进行改进,规则如下：对于每只蚂蚁k，路径记忆向量Rk按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i，则其选择城市j作为下一个访问对象的概率如下:

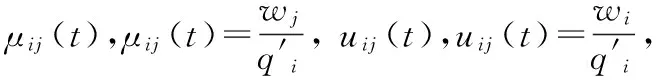
其中

式中，τij表示信息素浓度函数；ηij表示期望启发函数，ηij=1/dij；α、β、γ为相应的启发因子，是影响算法性能的关键参数，须经试验确定；R是在[0,1]上服从均匀分布的随机变量，R0(0≤R0≤1)是确定性选择初始概率参数；allowedk表示蚂蚁k下一步允许选择的需求节点集合。

2.3.2 改进信息素更新规则

2.3.3 局部优化策略

通过局部优化策略可以明显改善解的质量，很多学者采用不同的局部优化策略，如采用邻域搜索λ-Opt、swap和move算子、结合遗传算法等[24-26]，其中2-Opt算子[27]因其简单有效而得到广泛使用，本文也使用该算子对每辆车所走过的路线进行局部优化。

2.4 算法流程

求解CHVRPdw模型的算法框架可由图1所示。

3 仿真分析

3.1 模型对比分析

为了验证模型的有效性，这里暂不考虑车辆类型和数量约束，本文仅以路径最短为目标的CVRP模型、累计等待时间最短为目标的CCVRP模型和本文提出的以需求量加权累计等待时间最短为目标的单车型CHVRPdw模型(即CCVRPdw模型)进行对比，采用本文改进的MMAS算法求解，算法的有效性将在3.2节中通过实验予以说明。

数据采用http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/网站上下载的CVRP算例中的A-n32-k5进行实验，共32个坐标的随机节点，其中第1个节点为中心车场，其余31个节点具有随机的需求量，车辆容量为100，可用车辆数为6(如果不限定车辆数，则所有节点与中心节点相连所构成的路径为CCVRP最优解，问题失去研究意义)，速度为1。

本文以CVRP模型为基础，通过控制变量实验，确定各参数的最优值为：确定性选择概率参数R0=0.7，初始信息素浓度τ0=10，信息素挥发因子ρ=0.3，信息素启发因子α=1，期望启发因子β=2，可载率启发因子γ=1，蚂蚁数量M=33，迭代次数T=150；确定算法中参数最优值为：正确决策概率Pbest=0.05，信息素阈值最小个数k=2，当k取值较大时容易导致收敛过慢甚至不收敛，取1时候这种情况又过于苛刻，容易导致平滑操作的失效，从算法实验的经验来看，取k=2比较合适。同理，平滑系数δ=0.6。

本测试通过硬件平台：Intel(R) Core(TM)2 Duo CPU T6500 @2.10GHz，RAM 5G和软件平台：Matlab R2014b共同实现。每个模型分别进行20次独立的运算，Best代表20次中的最优结果，Average代表20次平均优化结果。运算结果见表1，三类模型的收敛曲线分别如图2～图4所示。

通过模型对比实验可以发现，对应CVRP模型真实路径长度最短得到的路径安排方案在累计等待时间上并不存在优势，也就是说，虽然整体运输成本最低，但对于应急情况来说，真实路径长度最优的方案并没有实际意义；对应CCVRP模型累计等待时间最短得到的路径安排方案虽然调用车辆数和真实路径长度都不是最优，但是充分体现了公平性，使整体节点的应急时间缩短到最优。相较前两者，对应CCVRPdw模型得到的需求量加权累计等待时间最短的路径兼顾时效性与公平性，使整体物资的运输时间达到最短，体现了系统优化的思想。其实质就是以真实路径长度和车辆数的很小损失来换取应急时间的最优，在应急情况下是完全可以接受的。

3.2 算法对比分析

为了验证算法的有效性和优越性，本文将基本MMAS算法和改进MMAS算法求解CHVRPdw模型进行对比。对于CHVRPdw模型，目前没有公开算例可以使用。为说明改进策略，分别采用A-n32-k5、A-n55-k9、B-n38-k6、B-n57-k7作为测试算例进行替代，其中车型参数人为设定。

车型参数R=(M,L,Q,V)，其中，车型编号M={1,2,3}，车型数量L1={2,3,4}，L2={4,5,6}车型容量Q={120,100,80}，车型速度V={0.8,1,1.2}。

将蚂蚁数量M设为节点数n+1，基本MMAS算法中可载率启发因子γ=0，其他算法参数设置参考3.1节。实验共进行10次，选择最优的结果记为Best，平均最优值记录为Average，最优加权累计等待时间对应的真实路径长度记录为RealLength，默认使用全部车辆，这样才能使得结果最优。运算结果见表2。

从实验中任选一组来直观比较两种算法的收敛情况，其收敛曲线见图5。

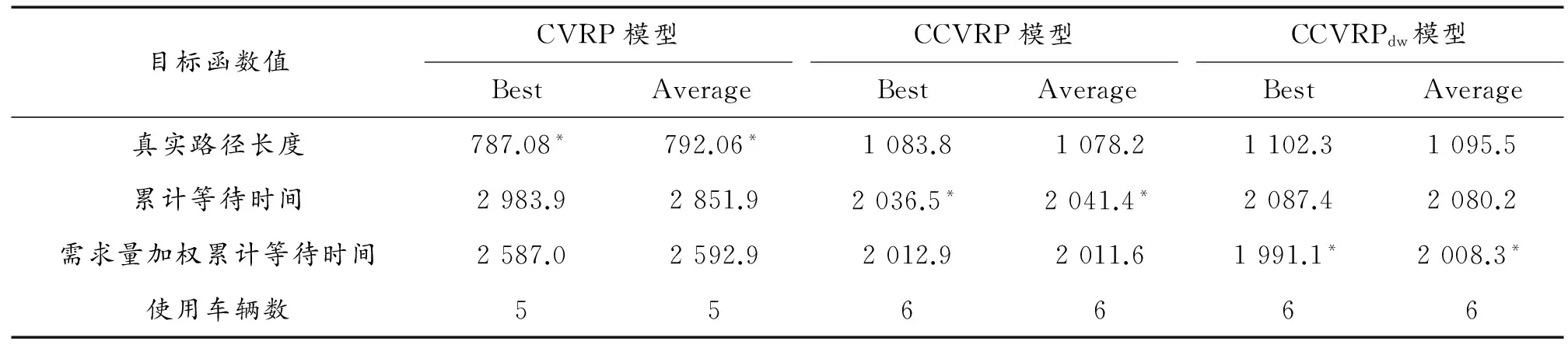
表1 模型对比分析结果

注：*表示该模型是以此项为目标函数，其余各项数值是根据该项优化值对应的最优路径计算得到。

表2 算法对比分析结果

通过算法对比可以发现，本文提出的MMAS算法改进策略对解决CHVRPdw问题具有很好效果，尤其是规模越大、效果越明显，验证了改进算法的有效性和优越性。对比3.1节与3.2节中A-n32-k5算例也会发现，虽然在增加车型和车数的基础上加权累计等待时间有了较大缩短，但是相应真实的总路程长度也增加很明显，因此需要在未来研究中对此加以讨论，即如何科学平衡应急点的需求和应急系统的整体成本。

4 结论

本文通过重新定义应急车辆路径优化问题的时效性和公平性概念，提出应急情况下优化目标必须同时兼顾时效性和公平性的原则，进而在CCVRP模型基础上首次提出考虑需求量加权的累计等待时间和多种车型同时存在情况下的CHVRPdw数学模型。同时，首次使用最大最小蚁群算法MMAS 来解决CHVRPdw模型问题，并有针对性的进行了算法改进，取得了较为明显的效果。本文工作对应急车辆路径问题研究具有启发意义，对蚁群算法在多车型车辆路径问题中的应用研究也有一定借鉴作用。由于篇幅所限，本文并未对大量算例进行仿真实验，算法的收敛性有待进一步验证，解的质量有待进一步提高。对于实际应急情况下的多车型车辆路径问题，还需考虑不同车辆类型的运输网络不同、通道可靠程度不同以及动态环境等问题，有待未来进行深入研究。

：

[1] CAMPBELL A M,VANDENBUSSCHE D,HERMANN W.Routing for relief efforts[J].Transportation Science,2008,42(2):127-145.

[2] NIKOLAKOPOULOU G,KORTESIS S,SNEFAKI A,et al.Solving a vehicle routing problem by balancing the vehicles time utilization[J].European Journal of Operational Research,2004,152:520-527.

[3] ZHANG X,MA H H,LIU W L,et al.Ant colony algorithm for vehicle routing problem with shortest completion time[C].The Proceedings of the 13th International Conference on Industrial Engineering and Engineering Management,2006:2928-2933.

[4] 刘霞，齐欢.最小-最大车辆路径问题的禁忌搜索算法[J].系统工程,2007,25(1):46-52.

[5] NGUEVEU S U,PRINS C,CALVO R W.An effective memetic algorithm for the cumulative capacitated vehicle routing problem[J].Computers & Operations Research,2010,37(11):1877-1885.

[6] RIBEIRO G M,LAPORTE G.An adaptive large neighborhood search heuristic for the cumulative capacitated vehicle routing problem[J].Computers & Operations Research,2012,39(3):728-735.

[7] KE L J,FENG Z R.A two-phase metaheuristic for the cumulative capacitated vehicle routing problem[J].Computers & Operations Research,2013,40(2):633-638.

[8] OGRYCZAK W.Inequality measures and equitable locations[J].Annals of Operations Research,2009,167(1):61-86.

[9] GOLDEN B L,ASSAD A,LEVY L,GHEYSENS R.The fleet size and mix vehicle routing problem[J].Computers & Operations Research.1984,11(1):49-66.

[10]李军,郭耀煌.物流配送牢辆优化调度理论与方法[M].北京:中国物资出版社,2001:1-90.

[11]FU L P.Scheduling Dial-a-ride Para-transit Under Time-varying,Stochastic Congestion[J].Transportation Research Part B,2002,36(6):485-506.

[12]BERNHARD F,MARTIN G.Time-Varying Travel Times in Vehicle Routing[J].Transportation Science,2004,38(2):160-173.

[13]王晓博,李一军.电子商务环境下物流配送中心选址模型与评价方法[J].系统工程理论方法，2006,15(3):199-204.

[14]葛显龙,许茂增,王伟義.多车型车辆路径问题的量子遗传算法研究[J].中国管理科学.2013,21(1):125-133.

[15]COLORNI A,DORIGO M,MANIEZZO V,et al.Distributed optimization by ant colonies[C].Proceedings of the 1st European Conference on Artificial Life,1991:134-142.

[16]GAMBARDELLA L M,DORIGO M.Ant-Q:A reinforcement learning approach to the traveling salesman problem[C].Proceedings of the 12th International Conference on Machine Learning,1995:252-260.

[17]DORIGO M,MANIEZZO V,COLORNI A.Ant system:Optimization by a colony of cooperating agents[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B,1996,26(1):29-41.

[18]GAMBARDELLA L M,DORIGO M.Solving symmetric and asymmetric TSPs by ant colonic[C]//Proc of the IEEE Conference on Evolutionary Computation.1996,622-627.

[19]DORIGO M,GAMBARDELLA L M.Ant Colony System:A Cooperative Learning Approach to the Traveling Salesman Problem[J].IEEE Transactionson Evolutionary Compution,1997,1(1):53-66.

[20]STUTZLE T,HOOS H.The MAX-MIN ant system and local search for the traveling salesman problem[A].IEEE International Conference on Evolutionary Computation and Evolutionary Program-ming Conference[C].Proceedings of IEEE-ICEC-EPS’97,1997:309-314.

[21]DORIGO M,BIRATARI M,STUTZLE T.Ant colony optimization:Artificial ants as a computational intelligence technique[J].IEEE Computational Intelligence Magazine,2006,1(4):28-39.

[22]FAVARETO D,MORETTI E,PELLEGRINI P.On the explorative behavior of max-min ant system[M].International Workshop on Engineering Stochastic Local Search Algorithms.Designing,Implementing and Analyzing Effective Heuristics,Springer Berlin Heidelberg,2009:115-119.

[23]STUTZLE T,HOOS H H.MAX-MIN Ant System[J].Future Generation Computer System,2000,16:889-914.

[24]BRAYSY O,GENDREAU M.Vehicle routing problem with time windows,Part I:Route construction and local searchalgorithms[J].Transportation Science,2005,39(1):104-118.

[25]SUBRAMANIAN A,DRUMMOND L M A,BENTES C,et al.A parallel heuristic for the vehicle routing problem with simultaneous pickup and delivery[J].Computers &Operations Research,2011,37(11):1899-1911.

[26]SUBRAMANIAN A,UCHOA E,OCHI L S.A hybrid algorithm for a class of vehicle routing problems[J].Computers &Operations Research,2013,40(10):2519-2531.

[27]HASEGAWA M,IKEGUCHI T,AIHARA K.Combination of chaotic neurodynamic with the 2-opt algorithem to solve traveling salesman problems[J].Physical Review Letters,1997,79(12):2344-2347.