空间漫反射基准星的辐射传递误差分析

陈轩 梅强 齐文雯 徐鹏



空间漫反射基准星的辐射传递误差分析

陈轩1,2梅强1,2齐文雯1,2徐鹏1,2

（1 北京空间机电研究所，北京 100094）（2 先进光学遥感技术北京市重点实验室，北京 100094）

为了解决现有定标方法的精度和频次不高的问题，提出一种基于基准星的全谱段、全孔径的在轨绝对辐射定标方法，方法适用于可见光和近红外谱段，辐射定标中的辐射基准可溯源至SI（国际单位）。文章简单介绍了遥感器在轨绝对辐射定标不确定度，并对基准星辐射定标的原理进行了分析。结合定标辐射传递模型和定标约束条件，对基准星辐射定标的不确定度进行分析，得到辐射传递的不确定度为1.03%。分析结果对提高遥感器在轨辐射定标精度提供了理论基础。

绝对辐射定标 基准星 辐射基准传递 不确定度 航天遥感

0 引言

在轨绝对辐射定标是遥感器入轨后需要不断完善的工作，是遥感卫星对地观测的前提。辐射定标发展的过程，从实验室定标——场地定标（包含交叉定标）——星上定标器定标——稳定的自然辐射源定标（基准星定标、月球定标），是一个从地面研制阶段向在轨全寿命周期发展的过程，也是遥感器定标精度质变的过程。随着在轨卫星数量和空间活动的不断增加，对地观测的频率和遥感数据量也不断增加，提高遥感器辐射定标精度已迫在眉睫[1]。

当前，遥感器的在轨绝对辐射定标多采用场地定标方法[2]，利用均匀的、变化率小的地面校正场，对遥感器进行定标，原理简单且可行性高，定标不确定度在5%左右，但该方法受大气条件和地物特征影响较大，定标精度难以进一步提高；太阳漫反射板定标[3-4]是在特定时刻，遥感器接收漫反射板反射太阳辐射能，实现在轨定标，不确定度优于3%，但漫反射板增加平台质量，易受卫星排出物污染，通过辐射基准传递方式、漫反射板研制等方面改进，定标精度仍有提升空间。

研究人员围绕辐射基准溯源和定标不确定度分析做了大量研究，文献[5]建立了以空间低温辐射计为辐射初级基准，太阳作为光源，具备在轨溯源能力的遥感器辐射定标传递链路，辐射基准传递不确定度为0.75%；文献[6]提出在明确辐射精度的约束条件下计算精度，可提高遥感器辐射定标精度的横向可比性，给出在不同谱段遥感器绝对辐射定标精度计算方法；文献[7]提出一种大视场可见光近红外的全光路全视场的在轨辐射定标方法，绝对辐射定标精度优于5%；文献[8]针对传统遥感器太阳漫反射板定标方法进行研究，首次提出星上定标时机的选择，并对定标的不确定度进行分析，不确定度优于2.04%。

针对上述研究情况，提出一种基准星（Proper Satellite，PS）辐射定标方法。根据TRUTHs计划[9]和漫反射板定标的研究思路，选取太阳作为辐射传递初级基准，建立可溯源至SI（国际单位）的辐射基准传递，实现高精度、高频次的基准星辐射定标。本文介绍了在轨辐射定标误差分析方法，结合基准星定标辐射传递模型和定标约束条件，分析了由各定标误差源引起的不确定度，并给出不确定度的预估。

1 在轨辐射定标精度分析

遥感器在轨定标精度计算是通过比对目标的绝对辐亮度值与遥感器对目标辐亮度测量值之间差异得出。在遥感器辐射响应关系为线性的前提下，定标表达式为

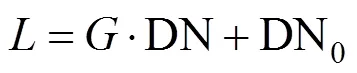
式中为辐亮度；为遥感器绝对定标系数；DN0为遥感器输出的零位计数值；DN为遥感器图像的数字计数值。

基准星作为待定标卫星的二次光源，入射到遥感器入瞳处的辐亮度为c，相应的信号输出为DNc；测量特定目标，遥感器入瞳处辐亮度为t，测量目标的输出信号为DNt，则

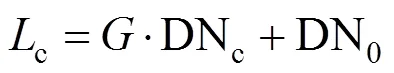
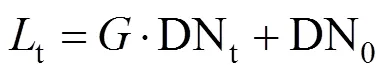
在假定经过暗电流校正的条件下，对系统模型进行简化，则有

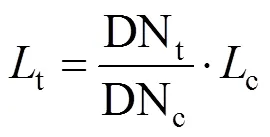
基准星绝对辐射定标的不确定度可由定标过程中的合成不确定度表示

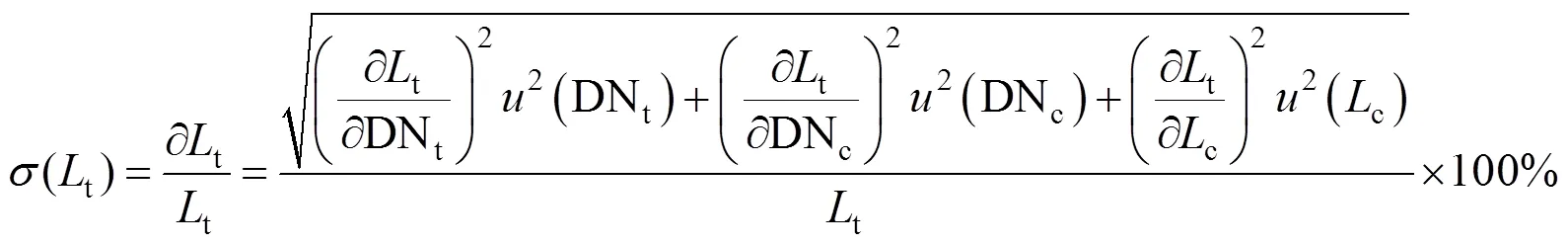
简化后，得出

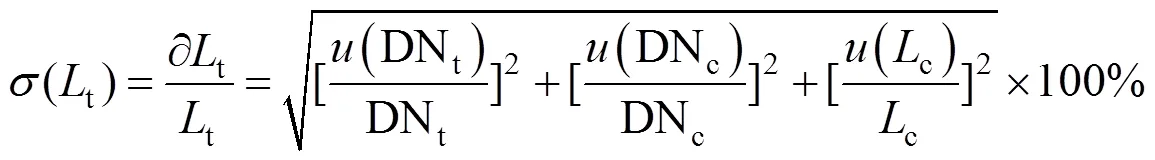
2 基准星辐射定标系统

基准星辐射定标系统（Proper Satellite Radiometric Calibration System，PSRCS）由地心坐标系下的太阳和位于太阳同步轨道的基准星、待定标卫星组成，如图1所示。基准星定义为一颗或多颗搭载着漫反射板反射体的卫星。辐射传递过程为：通过反射和衰减太阳辐射能，基准星将合适强度的能量间接引入待定标遥感器入瞳处，实现在轨绝对辐射定标。太阳作为定标辐射初级基准，辐射传递可实现在轨溯源至SI。定标辐射传递摆脱大气传输路径，避免了大气条件引起的不确定度，显著提高在轨绝对辐射定标精度。

2.1 定标辐射传递模型

基准星辐射定标针对可见近红外谱段，根据普朗克黑体辐射原理及辐射距离平方反比定律[10]，得到太阳辐射出射度和入射到基准星漫反射板表面的辐照度PS

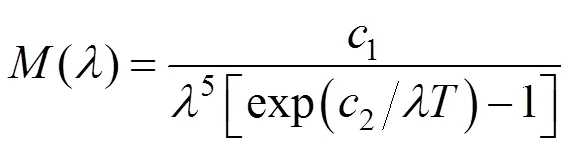
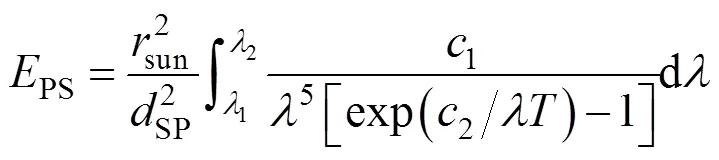
式中1为第一黑体辐射常数；2为第二黑体辐射常数；SP为太阳与基准星的相对距离；sun为太阳半径；为太阳平均温度；为波长，1~2为任意连续谱段。太阳等效为一个5 800K的黑体，为了降低定标辐射基准源的不确定度，结合现有太阳辐照度数据库，利用太阳光谱仪，对太阳辐照度进行实时监测。

漫反射板反射特性是用漫反射定律（朗伯反射）来描述，即以双向反射率分布函数（BRDF）来描述[11]，漫反射板可视为由不同的小面元组成。假设定标过程中，待定标遥感器的视轴方向始终保持垂直于漫反射板表面。计算出待定标遥感器接收的基准星反射的辐亮度为RS[12]

式中SP为太阳光入射在漫反射板的入射角，即太阳入射光线与漫反射板法线的夹角；PR为待定标遥感器在漫反射板的出射角，即遥感器视轴与漫反射板法线的夹角；为定标时漫反射板的衰减系数。

2.2 定标约束条件

（1）基准星与待定标卫星的距离约束

考虑到遥感卫星平台的搭载能力，漫反射板尺寸需满足定标孔径的要求，待定标遥感器对漫反射板的成像分辨率进行限定，在漫反射板尺寸确定的前提下，约束了待定标卫星与基准星的相对距离。根据光学遥感成像比例尺的定义，结合待定标遥感器的光学系统参数，得到两卫星之间的理论最大相对距离。

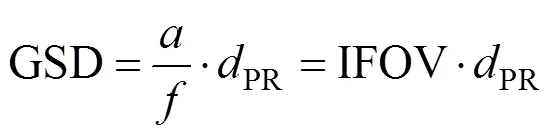
式中为卫星CCD探测器的像元尺寸；为相机焦距；GSD为遥感器对漫反射板的空间分辨率；PR为两卫星之间的距离；IFOV为待定标遥感器的瞬时视场角。研究表明，定标源对待定标遥感器的成像角分辨率不小于10个像元时，可定义为有效定标源[13-14]。

（2）遥感器辐射响应的动态范围约束

根据基准星定标的辐射传递过程，漫反射板通过反射、衰减，将适合强度的太阳辐射引入到待定标遥感器。遥感器对入射到其入瞳前的太阳辐亮度存在辐射响应的最大值和最小值，并且辐亮度受到太阳光与漫反射板法线和漫反射板法线与待定标遥感器视轴的夹角影响。辐亮度必须满足遥感器辐射响应的动态范围，才能用于在轨辐射定标。在此约束中，角度是影响辐亮度传递主要的变量。

2.3 漫反射板衰减特性监测

漫反射板衰减特性的监测方法包含太阳绝对比辐射计方法和双漫反射板方法。太阳绝对比辐射计方法是对太阳辐射能量和漫反射板反射辐射能量的辐射比进行测量，实现长期稳定性监测[15]；双漫反射板方法是采用保存完好且仅用于监测测量的参考漫反射板对暴露在空间环境中发生衰减的工作漫反射板进行相对测量，实现长期稳定性监测[16]。两种衰减监测方法都已实现在轨应用。

基准星辐射定标选取太阳绝对比辐射计方法，实现对基准星漫反射板全寿命周期衰减特性的实时监测和修正。基于比值测量的方法，以入轨首次定标时刻的衰减测量为基准，同时接收定标时刻太阳总辐亮度和漫反射板反射辐亮度并计算辐射比，与首次定标时刻的监测数据比较，实现对漫反射板衰减特性的监测。同时，太阳绝对比辐射计可实时监控太阳辐射出射度的稳定性，保证基准星辐射传递中辐射初级基准的精度，降低基准星辐射传递的不确定度。

3 基准星辐射传递不确定度分析

基准星辐射定标系统中，太阳、基准星、待定标卫星都是运动的天体，卫星的空间位置随时间的变化导致彼此相对距离和夹角时刻发生改变。辐射传递的不确定度不能够静态分析，应动态地对各误差源产生的不确定度进行分析。依据基准星辐射传递模型可知，基准星定标辐射传递的误差源主要包含太阳、距离、角度、漫反射板。结合式（9）、（10），基准星辐射传递精度由合成不确定度表示

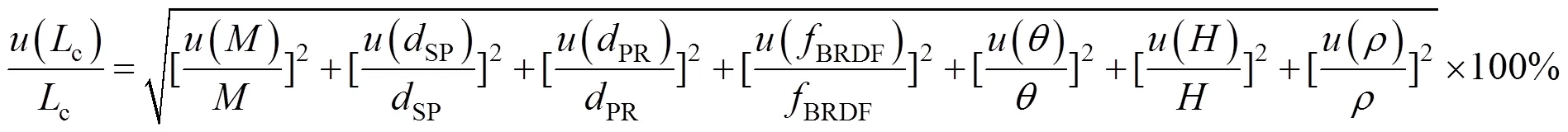
式中为基准星辐射传递中的测量角度；为漫反射板面型系数。

对不同误差源引起的合成不确定度分量进行系统分析：

（1）太阳辐射出射度引起的不确定度（）

太阳是基准星辐射传递链路中的初级辐射基准，遵循朗伯球体辐射定律。在辐射传递模型中，依据普朗克黑体辐射理论，可等效地对太阳光进行仿真分析。研究人员对大气层外的太阳辐照度进行长期的监测，经统计得出辐照度不确定度优于0.3%[17]。

（2）基准星定标距离PR和SP引起的不确定度（PR）和（SP）

基准星的轨道选取太阳同步轨道，基准星辐射定标系统主要针对太阳同步轨道的遥感卫星，轨道高度一般在400~1 000km之间，结合辐射传递模型和定标约束对定标距离引起的不确定度进行分析。

太阳与基准星的相对距离SP测量中，基准星的轨道为太阳同步轨道，太阳与基准星的相对距离SP可近似为太阳与地球的相对距离，即1AU。假定定标距离测量误差为1km，和太阳与基准星的相对距离相比，变化量可忽略，距离测量不确定度亦可忽略。

对基准星与待定标卫星的相对距离PR分析，如图2所示，待定标遥感器的焦距选取3~10m，遥感器的像元选取6~10μm，得出瞬时视场角IFOV为0.6×10–3~3.3×10–3mrad；定标漫反射板尺寸选取1，2，4m，得出待定标遥感器对漫反射板的空间分辨率为0.1，0.2，0.4m。根据式（10），可得出基准星与待定标卫星的相对距离理想最大值。由于两星之间的相对距离随时间发生变化，假定定标距离测量误差为1km时，距离测量不确定度如图3所示。

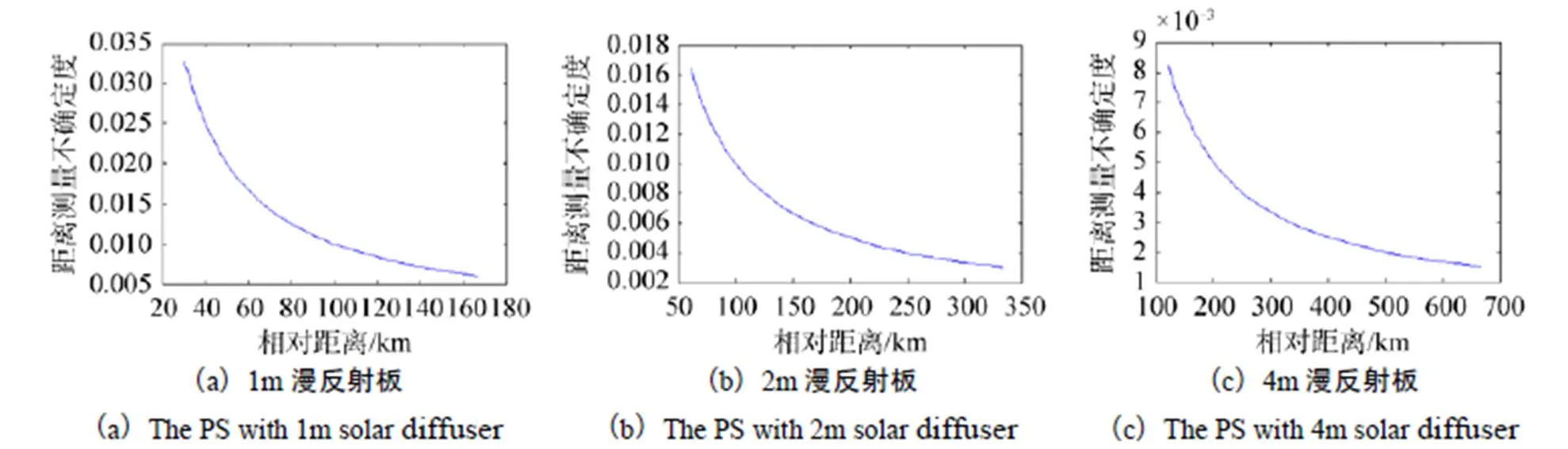
图3 搭载不同漫反射板的基准星与待定标卫星的距离测量不确定度

由图3分析可知，定标距离测量不确定度随基准星与待定标卫星的相对距离增大而减小；基准星与待定标卫星相对距离的理论最大值随漫反射板尺寸的增大而增大。以“高分二号”（GF-2）卫星和2m漫反射板为例，GF-2卫星的焦距为7.785m，像元尺寸为10μm，遥感器对漫反射板的空间分辨率应不大于2m/10，即0.2m，计算得出基准星与GF-2卫星的相对距离为155.7km。距离测量的不确定度为0.6%。

（3）基准星辐射传递测量角度引起的不确定度（）

依据基准星辐射传递模型，辐射传递夹角包括太阳入射光与漫反射板法线的夹角和遥感器视轴方向与漫反射板法线夹角。已知遥感器的辐射响应动态范围的前提下，可计算辐射传递的三者夹角范围。分析中以GF-2卫星遥感器辐射响应动态范围为例，得出测量角度的范围为（0°，86°）。测量角度引起的不确定度（）的计算公式为[18]

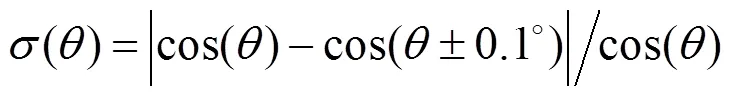
基准星辐射定标的角度测量不确定度曲线如图4所示，当小于60°时，角度测量不确定度增长缓慢；当大于60°时，角度测量不确定度增长加速。现有在轨漫反射板定标中，太阳入射到漫反射板的角度控制在小于60°，此时角度测量误差为0.1°，以最大定标角度计算角度测量不确定度为0.3%。

（4）漫反射板BRDF引起的不确定度（BRDF）

漫反射板的双向反射分布函数（BRDF）是基准星定标辐射传递中的重要环节。在实验室中，针对不同谱段，以入射角和出射角作为变量，分步长对BRDF进行绝对测量。通过固定入射光方向或探测器接收方向的角度，分段改变另一方向角度，进而测量探测器接收到的辐亮度，从而得出漫反射板的BRDF，国内绝对测量不确定度可达到1%[19]。

（5）漫反射板面型系数引起的不确定度（）

基准星辐射传递过程中，太阳辐射能传递到漫反射板，可覆盖整个漫反射板的工作区域，漫反射板的面型均匀性对基准星定标辐射传递有很大影响。当成像角分辨率满足不小于10个像元的情况下，可包含不少于8个完整的像元。理论上，8个像元接收的辐射响应峰值最大且近似相同。定标过程中，基准星漫反射板暴露在空间环境，主要受到温差和力学等影响。其中，在定标时刻和非定标时刻的漫反射板表面温差会造成板严重形变，导致漫反射板的面型均匀性下降，辐射传递精度降低。漫反射板可通过拼接的方式，将漫反射板拆分成小块，从而抵抗温差对漫反射板面型的影响，当拼接漫反射板的小块足够多时，可近似消除拼接间隙对辐射响应峰值的影响；对基准星漫反射板的力学影响主要体现振动对定标辐射传递产生的影响，将基准星振动和待定标卫星振动结合在一起分析，即在0时刻，满足遥感器对漫反射板成像分辨率的条件下，相应数量的像元接收到相等且满足定标的辐射响应峰值，1时刻卫星振动造成：用于定标的像元数量不满足定标的成像角分辨率条件；用于定标的接收到辐射响应峰值的完整像元中加入非峰值像元，探测器接收的漫反射板传递的太阳辐射绝对测量值下降。可通过对辐射传递进行像质振动补偿，将分散的辐射能量二次计算，保证太阳辐射绝对测量值。同时，针对基准星辐射定标，待定标卫星应具备一定的指向精度和姿态稳定度，保证定标的正常进行。在实验室中测试的漫反射板的面型不确定度为1%。

（6）漫反射板衰减系数引起的不确定度（）

漫反射板的衰减系数的监测是长期过程，持续遥感器在轨运行的全寿命周期。衰减系数的监测方法为在相同角度、谱段范围条件下，利用太阳绝对比辐射计对漫反射板的反射辐亮度和太阳总辐亮度的辐射比进行相对测量，方法以首次定标时刻的监测数据为基础，实现对漫反射板衰减系数的监测，测量不确定度优于0.88%[20]。

4 基准星辐射传递不确定度预估

不确定度分析中的误差包含系统误差和随机误差，随机误差无规律可寻且大小不定；系统误差存在一定特征规律，一定程度上可进行减小或消除。表1列出了基准星辐射传递模型的主要误差源及其不确定度。

表1 基准星辐射传递模型不确定度

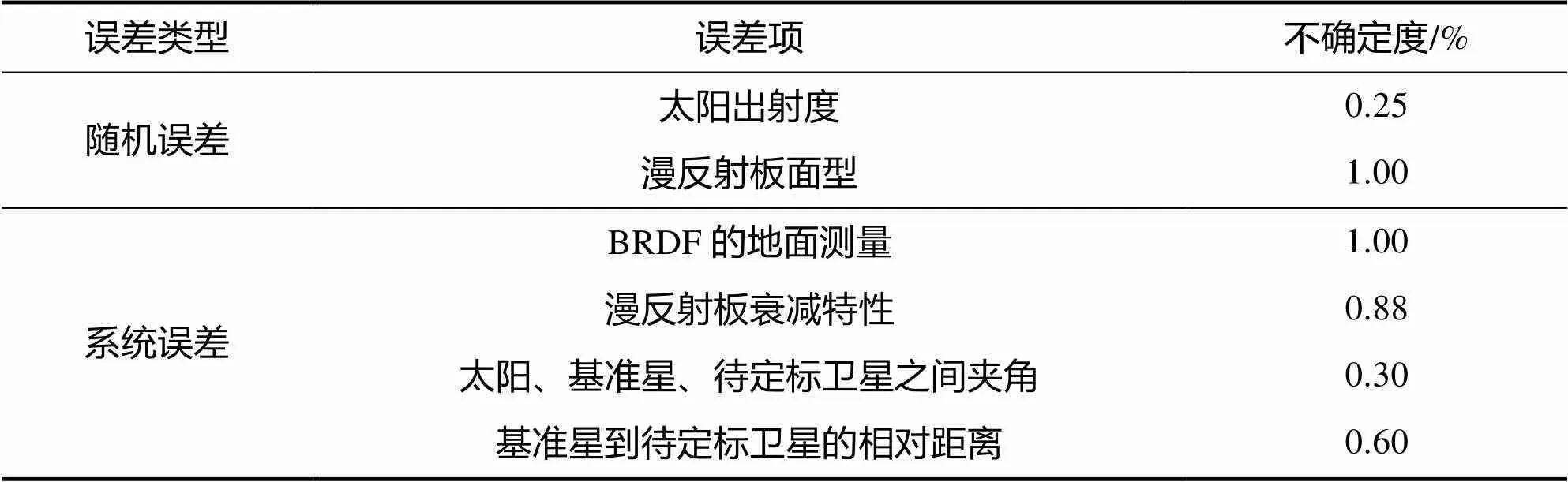
Tab.1 Uncertainty of the PS radiation transfer model

由表1可知，漫反射板BRDF测量、漫反射板衰减特性、三者的夹角和两星之间的相对距离为系统误差，通过进行大量试验测量，分析各自误差分布规律，进而规避、减小各误差对基准星辐射定标的影响。辐射传递不确定度主要由太阳出射度和漫反射板面型的随机误差引起的不确定度组成，计算得出不确定度为1.03%。

5 结束语

与现有在轨辐射定标方法相比，基准星辐射定标方法摆脱大气条件和地物特征对在轨定标精度的限制，选取太阳作为辐射基准，定标辐射基准传递可溯源至SI，显著提高在轨辐射传递精度。辐射传递不确定度分析基于基准星辐射定标的辐射传递模型和定标约束条件得出。通过区分误差源，系统分析传递链路中各不确定度，计算得出不确定度优于1.03%。本文中不确定度数据是根据漫反射板定标相关研究总结得出，后期研究工作中，还应基于基准星辐射传递，选取不同漫反射板材料对辐射传递进行实际测量分析。基准星辐射传递不确定度分析理论上验证了定标的可行性，为遥感器在轨辐射定标精度、定标频次的提高提供了参考。

[1] 朱军, 吴雁林, 沈中, 等. 环境-1A、B卫星CCD相机系统级辐射定标数据分析[J]. 航天器工程, 2009, 18(5): 73-79. ZHU Jun, WU Yanlin, SHEN Zhong, et al. Analysis of System-level Radiometric Calibration Data for HJ-1A/B Wide Coverage Camera[J]. Spacecraft Engineering, 2009, 18(5): 73-79. (in Chinese)

[2] ARAI K. Comparison Among Cross, Onboard and Vicarious Calibrations for Terra/ASTER/VNIR[J]. International Journal of Advanced Research in Artificial Intelligence, 2013, 2(10): 14-18.

[3] SLATER P N, BIGGAR S F, THOME K J, et al. Vicarious Radiometric Calibrations of EOS Sensors[J]. Journal of Atmospheric & Oceanic Technology, 2009, 13(2): 349.

[4] 徐伟伟, 张黎明, 杨本永, 等. 基于多灰阶靶标的在轨辐射定标方法研究[J]. 光学学报, 2012, 32(2): 157-161. XU Weiwei, ZHANG Liming, YANG Benyong, et al. On-orbit Radiometric Calibration Based on Gray-scale Tarps[J]. Acta Optica Sinica, 2012, 32(2): 157-161. (in Chinese)

[5] 王玉鹏, 胡秀清, 王红睿, 等. 可在轨溯源的太阳反射波段光学遥感仪器辐射定标基准传递链路[J]. 光学精密工程, 2015, 23(7): 1807-1812. WANG Yupeng, HU Xiuqing, WANG Hongrui, et al. Standard Transfer Chain for Radiometric Calibration of Optical Sensing Instruments with Traceability in Solar Reflective Bands[J]. Optics and Precision Engineering, 2015, 23(7): 1807-1812. (in Chinese)

[6] 龙亮, 王世涛, 周峰. 航天遥感器辐射定标精度计算方法研究[J]. 航天返回与遥感, 2012, 33(6): 51-55. LONG Liang, WANG Shitao, ZHOU Feng. Research on Calculation Method of Space Remote Sensor’s Radiometric Calibration Accuracy[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(6): 51-55. (in Chinese)

[7] 赵艳华, 董建婷, 张秀茜, 等. 漫反射板全光路全视场全口径在轨辐射定标技术[J]. 航天返回与遥感, 2016, 37(2): 92-99. ZHAO Yanhua, DONG Jianting, ZHANG Xiuqian, et al. In-orbit Radiometric Calibration Technology Based on Diffuse Reflection Plate in Full Bore, Full FOV and Full Optical Path[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(2): 92-99. (in Chinese)

[8] 黄文薪, 张黎明, 司孝龙, 等. 基于太阳漫射板的星上定标方法研究[J]. 光谱学与光谱分析, 2017, 37(3): 952-957. HUANG Wenxin, ZHANG Liming, SI Xiaolong, et al. The Research of On-orbit Calibration Method Based on Solar Diffuser[J]. Spectroscopy and Spectral Analysis, 2017, 37(3): 952-957. (in Chinese)

[9] FOX N A, KAISSER W W, SCHMUTZ K T, et al. Accurate Radiometry from Space: An Essential Tool for Climate Studies[J]. Philosophical Transactions of the Royal Society of London, 2011, 369(1953): 4028-4063.

[10] 顾行发, 田国良, 余涛, 等. 航天光学遥感器辐射定标原理与方法[M]. 北京: 科学出版社, 2013: 72-126. GU Xingfa, TIAN Guoliang, YU Tao, et al. Radiometric Calibration Theory and Method of Space Optical Sensors[M]. Beijing: Science Press, 2013: 72-126. (in Chinese)

[11] 梁顺林, 李小文, 王锦地. 定量遥感[M]. 北京: 科学出版社, 2013. LIANG Shunlin, LI Xiaowen, WANG Jindi. Quantitative Remote Sensing of Land Surface[M]. Beijing: Science Press, 2013. (in Chinese)

[12] 赵彬, 杨苏辉, 王世涛, 等. 空间小目标的光学建模与模拟观测[J]. 光学学报. 2009, 29 (12): 3395-3403. ZHAO Bin, YANG Suhui, WANG Shitao, et al. Optical Modeling and Simulative Survey of Small Objects in Space[J]. Acta Optica Sinica, 2009, 29 (12): 3395-3403. (in Chinese)

[13] HUGH H K, JAMES M A, KRIS J B. Radiometric Calibration of Spacecraft using Small Lunar Images[J]. Proceedings of SPIE, 1999, 3870: 193-205.

[14] KIEFFER H, JARECKE P, PEARLMAN J. Initial Lunar Calibration Observations by the EO-1 Hyperion Imaging Spectrometer[J]. Proceedings of SPIE, 2002, 4480: 247-258.

[15] XIONG X X, ANGAL A, SUN J Q, et al. On-orbit Performance of MODIS Solar Diffuser Stability Monitor[J]. Journal of Applied Remote Sensing, 2014, 083514: 08351401-08351414.

[16] OLIJ O, BAUDIN G, BEZY J L, et al. Spectral on Diffuser Calibration for MERIS[J]. SPIE, 1997, 3221: 63-74.

[17] WIELICKI B A, YOUNG D F, MLYNCZAK M G, et al. Achieving Climate Change Absolute Accuracy in Orbit[J]. Bulletin of the American Meteorological Society, 2013, 94(10): 92-97.

[18] 杨本永, 张黎明, 沈政国, 等. 光学传感器星上定标漫射扳的特性监测[J]. 光学精密工程, 2009, 17(9): 1851-1868. YANG Benyong, ZHANG Liming, SHEN Zhengguo, et al. Characteristic Measurement of Diffuser Panel Used for On-board Calibration for Satellite Optical Sensors[J]. Opt. Precision Eng, 2009, 17(8): 1851-1868. (in Chinese)

[19] 李俊麟, 张黎明, 司孝龙, 等. 基于六轴串联机械手的双向反射分布函数测量装置[J]. 光学精密工程, 2014, 22(11): 2983-2989. LI Junlin, ZHANG Liming, SI Xiaolong, et al. BRDF Device Based on Six-axis Robot[J]. Optics and Precision Engineering, 2014, 22(11): 2983-2989. (in Chinese)

[20] 黄文薪, 张黎明, 司孝龙, 等. 星上反射率定标原理及其精度保持方法研究[J]. 光学学报, 2016(6): 258-265. HUANG Wenxin, ZHANG Liming, SI Xiaolong, et al. Theory of On-orbit Reflectance Calibration and the Study of Its Precision Maintenance Method[J]. Acta Optica Sinica, 2016(6): 258-265. (in Chinese)

（编辑：王丽霞）

Radiation Transfer Error Analysis of Space Diffuse Proper Satellite

CHEN Xuan1,2MEI Qiang1,2QI Wenwen1,2XU Peng1,2

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Key Laboratory of Advanced Optical Remote Sensing Technology of Beijing, Beijing 100094, China）

In order to solve the issue of the low accuracy and the low frequency of the existing calibration methods, a new method of on-orbit absolute radiometric calibration based on the full spectrum and the full aperture of the proper satellite is proposed. The method is suitable for visible and near-infrared spectra, and the calibration radiation standard can be traceable to SI. This paper briefly introduces the uncertainty of absolute radiometric calibration of remote sensors, and analyzes the principle of proper satellite radiometric calibration. Combined with the calibration radiation transfer model and the calibration constraints, the uncertainties of the proper satellite radiometric calibration are analyzed, and the uncertainty of radiation transfer is 1.03%. The analysis results could provide a theoretical foundation for the improvement of the on-orbit radiometric calibration accuracy of the remote sensors.

absolute radiometric calibration; proper satellite; radiation standard transfer; uncertainty; space remote sensing

TP79

A

1009-8518(2018)01-0053-08

10.3969/j.issn.1009-8518.2018.01.007

陈轩，男，1987年生，2013年获长春理工大学光学工程专业硕士学位，现在中国空间技术研究院飞行器设计专业攻读博士学位。研究方向为航天光学遥感技术。E-mail: cx1122pp@163.com.

2017-12-11

国家自然科学基金（61701023）