主成分分析中主成分个数的确定及其综合评价方法的讨论
2018-03-13
(兰州财经大学 甘肃 兰州 730000)
一、引言
主成分分析的思路是降维,通过对原始变量进行线性变换,从而形成新的变量。新的变量从个数上远远少于原始变量,但是其包含的信息与原始变量相差不多。从理论上讲,有多少个原始变量就可以提取多少个主成分,然而在线性变换之后,我们在降维和信息的保留上做出了权衡。目前在许多教科书以及实际研究工作中,对于主成分个数的保留有多种方法,如,特征值大于1,方差累计(信息保留)大于85%等等,它的优势在于简单且对绝大多数情况都适用。但是这些方法是经验性的,没有理论上的支持。
在主成分提取之后,我们还会遇到一个问题,就是提取后主成分的合理解释。由于主成分是原始变量的线性组合,通常我们用系数向量中绝对值较大的变量对该主成分下定义,然而,实际中,是不是所有的数据在提取主成分后都能够得到合理的解释,绝对值较大是怎样一个界限,负值系数该如何解释,都没有一个明确的规定。
关于样本主成分得分排序的问题,目前常用的方法是利用主成分做线性组合,并以每个主成分的方差贡献率作为权数构造综合评价函数。然而这种方法在实践中不够理想,最主要的原因是产生主成分的特征向量的各级分量符号不一致,很难进行排序评价[1]。改进的一种办法是只取第一主成分构造评价得分,前提是主成分系数全为正,也就是要求所有评价指标变量都是正相关。但是这样构造的评价函数并没有考虑提取的其它的主成分(当主成分个数大于1时),结论是否可靠呢?
基于以上的思考,本文在参阅相关文献的基础上加之个人的理解,对上述问题分别进行讨论,然后找到相对合理且具有理论支撑的一套从主成分提取到最后综合评价函数构造的方法。
二、问题的提出和讨论
1.主成分个数应当如何选定?
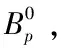
2.主成分是否能够有明确的解释?


我们知道,主成分之间是不相关的,在X为正向的前提下,主成分中载荷较大的指标变量同符号是相互促进的关系,不同符号是相互制约的关系。主成分中有正有负是多个相关变量相互有机联系在一起的正常表现。对于主成分合理的解释直接关系到在综合评价中构造综合评价函数对样品进行得分评价,因此,我们将主成分内部变量的符号解释成相互促进或者相互制约,而对于非正向主成分本身,在正向化之后,综合评价函数在方向上也应当是合理的。
3.如何构造综合评价函数使得样品评价得分更加合理?

三、实际数据应用
为了方便起见,本文采用《我国部分省、直辖市、自治区独立核算的工业企业经济效益评价》数据[1],该数据涉及28个样品,9项指标,x1到x9分别表示百元固定资产原值实现值(%)、百元固定资产原值实现利税(%)、百元资金实现利税(%),百元工业总产值实现利税(%)、百元销售收入实现利税(%)、每吨标准煤实现工业产值(元)、每千万时电力实现工业产值(元)、全员劳动生产率(元/人*年)以及百元流动资金实现产值(元)。
因为变量存在量纲不一致,我们从相关阵出发进行主成分分析。由于指标是正向的,因此首先,只需将X标准化,得到标准化后的变量间的相关阵。
我们发现x1与x2、x3、x6、x7、x8、x9具有高度相关性,可以通过主成分分析来进行降维处理。
接下来,从成分矩阵中寻找简单结构。在SPSS中我们设定提取特征值为0,可以得出全成分矩阵。
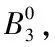
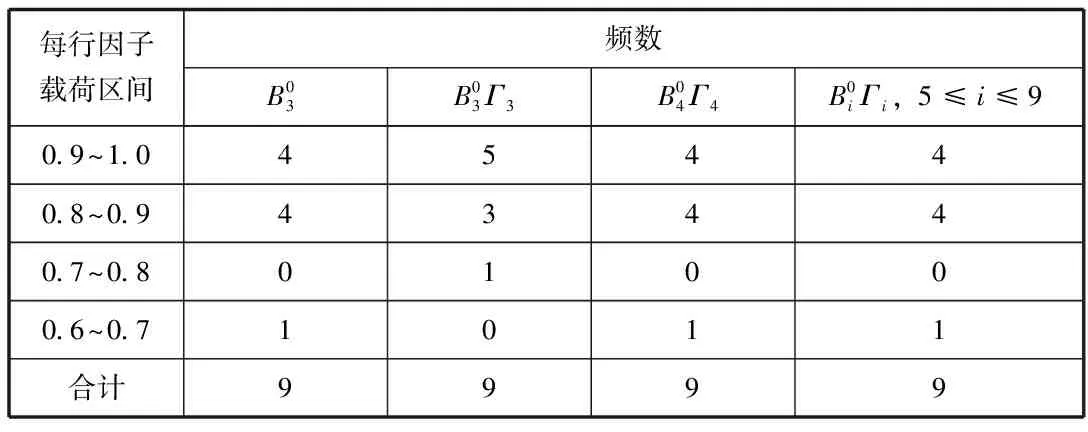
表1 载荷频数分布
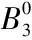
现在我们要通过显著相关来确定主成分的个数。由于样本数较小,给定显著性水平α=1%,查相关系数临界值表,得r0.005(26)≈0.487。从成分矩阵中我们找到每列元素中绝对值最大的与0.487比较,当第k+1列中绝对值最大元素小于0.487,则提取k个主成分。依据此,本例中,k=3,即提取3个主成分。在spss中主成分分析选项中我们固定提取3个主成分,得到方差贡献表,提取的3个主成分共解释了92.447%的总方差。
然后,我们通过成分载荷阵中Yj与X相关系数显著性对主成分进行解释说明。可以看到,Y1与x1、x2、x3、x6、x7、x8、x9具有显著的正相关性(与0.487比较);Y2与x4、x5具有显著的正相关性;Y3与x5具有显著的正相关性。其解释如下:
Y1:显著变量为x1、x2、x3、x6、x7、x8、x9,反映了工业企业生产中资金投入与劳动力产出之间具有相互促进的作用,作为第一主成分,还反映了投入产出是衡量企业经济效益的第一大要素;
Y2:显著变量为x4、x5,反映了企业效益(销售额)对利税积极的影响,在衡量经济效益时同时也要考虑产出对国家的贡献;
Y3:显著变量为x5,反映了企业收入对利税贡献的补充部分。
根据显著性,我们分别对主成分命名:Y1为企业投入产出水平;Y2为企业效益对利税的贡献水平;Y3为企业效益对利税贡献的补充部分。通过特征值及成分载荷,我们得到标准化后的主成分表达式为:
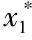
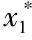
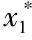
根据表达式,三个主成分在衡量企业经济效益上都是正向的,无需正向化。因此我们直接构造综合评价函数:
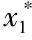
根据以上式子我们对样品进行成分得分和综合评价得分(取综合评价前10个城市得分):

城市Y综合序Y1序Y2序Y3序上海5051704113840255浙江26824372-18227-00516天津2663374405390196北京2374282524210662江苏22553943-28280169广东09961826-13226-04324山东06270987-0361600412云南0278-00212242-14328福建02490518-05218-03523湖北020100359-031500411
对于得分中的负值,其反映的是企业在该成分中的相对水平。由于第一主成分对于原始变量信息解释力最大,因此从上表我们也看出综合评价得分排序与按照第一主成分排序差异不大。
根据得分,对所有28个城市做系统聚类,方法使用平均联接法,从输出的谱系图上看到这28所城市在工业企业经济效益上分为4类:
第一类:陕西、新疆、吉林、四川、江西、内蒙古、宁夏、青海
第二类:福建、湖北、山东、安徽、河北、河南、湖南、广西、辽宁、黑龙江
第三类:贵州、甘肃、云南、山西
第四类:北京、天津、江苏、浙江、广东、上海
第一类在三个主成分得分上都偏低,说明是无论在企业的投入产出还是效益利税水平上都相对落后;第二类在三个主成分得分上属于一般水平;第三类虽然在第一主成分上的得分不高,但是相对来说,其销售收入和产值利税水平要高于其它城市;第四类在投入产出方面属于领先水平。
结合综合评价得分和主成分得分,我们对上海、浙江、云南三个地区进行企业效益评估。上海在投入产出上得分7.04远高于其它地区排名第一,对生产的高投入换来高回报,说明上海企业无论在管理、运营、产能、销售方面都具备较高的能力和效率。在效益利税方面,上海得分1.38,排名第四,说明上海企业在具备较高的经济利益的同时,对利税做出的贡献同样处于领先地位。浙江在投入产出上得分4.37,排名第二,但是在利税方面得分-1.82,排名27,这说明,浙江企业在经济效益较高的条件下,其产值和销售对于利税的贡献还远远不足,因此,有效的提升产品利润、监管税收是该地区的首要工作。云南在投入产出上得分-0.02,这说明云南较其他城市来说,投入产出基数和效率都不理想,然而云南在利税方面得分2.4位于全国第2,说明其利润率较高。
除此之外,我们还可以从聚类的结构中发现,企业经济效益和地域可能存在一定的相关性,但是从我们的数据中还无法获知。西部地区总体经济效益偏低,中部地区经济效益略好,首都和东部沿海地区经济效益较好,同时贵州、甘肃、云南、山西四个地区虽然在投入产出上较为落后,但是它们的利税水平较高,如何提高这些地区的投入产出水平,使其进一步提高利税贡献应该是需要深入研究的问题。
四、结论
通过上面的内容,我们有了完整的对于多指标数据进行主成分提取、分析和综合评价的方法,这个方法对于指标数据有一定的应用条件,标准化、正向、成分矩阵或者旋转后的因子载荷阵具有简单结构,主成分与变量有显著相关性。这也使得这种方法在对数据进行主成分分析的时候存在一定的局限性,但是我们看到,即便如此,只要前提条件满足的情况下,整个分析过程指标的选择、成分个数的选择、成分的解释命名方面都有理有据。同时这个方法对指标变量的信息做了最大化的保留,使得在成分得分和综合评价方面不会因为信息的大量遗漏而造成偏颇。
[1]多元统计分析第三版.何晓群.2004
[2]主成分分析综合评价应该注意的问题.林海明,杜子芳.统计研究2013.8
[3]因子分析应用中一些常见问题的解析.林海明.统计与决策.2012.15
[4]多指标综合评价中主成分分析和因子分析方法的比较.王文博.统计与信息论坛.2006.9
[5]多元统计分析引论.方开泰,张尧庭.科学出版社1982
