设计特征对水泥混凝土路面错台的敏感性分析

王威娜, 秦 煜, 吕昊文, 闫 强, 何晓英

(1. 重庆交通大学 交通土建工程材料国家地方联合工程实验室, 重庆 400074; 2. 重庆交通大学 土木工程学院, 重庆 400074; 3. 中铁二院重庆勘察设计研究院有限责任公司, 重庆 400023; 4. 广西交投科技有限公司, 广西 南宁 530021; 5. 重庆交通大学 河海学院, 重庆 400074)

横向接缝错台是水泥混凝土路面典型病害之一,直接影响行车舒适性与安全性.筛选对错台起主导作用的设计特征,全面掌握影响错台的设计特征,以在未来设计及性能预测中予以重视,有利于路面建养工作的有效开展.

文献[1]利用力学模型分析了设计特征对错台的影响.文献[2]基于实际数据定性分析了错台影响因素.美国国家公路和交通运输协会的《力学经验路面设计指南》指出影响错台的因素主要包括荷载、接缝传荷能力、基层和水[3].但上述研究均未对各因素的影响作用进行量化分析.有研究涉及了传力杆[4]、基层[5]等对错台的量化影响,但这些研究均是针对单一因素的量化分析.也有研究人员基于LTPP数据分析了错台各影响因素敏感性.文献[6]将20世纪90年代的LTPP数据分为有传力杆和无传力杆两大类,分别得到了有/无传力杆路面错台的影响因素重要程度排序.文献[7]基于截止2001年的LTPP(long-term pavement performance)数据,结合方差分析研究了各种因素对错台的影响.但由于数据库、数据分类方法与分析方法的不同导致研究结果有一定差异.因此,有必要基于不断更新的数据库,采用适合于数据特点的分析方法进行设计特征敏感性分析.

本研究基于较新LTPP错台数据,在比较相关分析[6]、方差分析[7]、灰色关联分析[8]、主成分分析法[9]和神经网络方法[10]这5种方法的基础上,结合图形分析,选择较优敏感性分析方法与关键设计特征,并结合关键设计特征,将错台数据分为有传力杆和无传力杆数据集,采用较优敏感性分析方法,研究影响有/无传力杆路面错台的设计特征的重要程度,提出抑制路面错台设计建议.

1 敏感性分析思路

本研究所用数据来源于美国路面长期使用性能研究项目LTPP中的普通水泥混凝土路面数据库GPS-3[11].错台数据采用佐治亚错台仪测得,数据截止于2011年.首先基于LTPP数据库建立数据集,选取未经过养护或维修的第一生命周期错台数据,去掉超出正负两倍的标准差以外的错台值,选取可能与错台发展相关的设计特征,整合包括错台数据与设计特征的数据库.所用数据共计192个样本点,错台最大量从0～7.8 mm.采用接缝状况、路肩传荷能力、路肩基层支撑能力、地基复合模量、基层冲刷系数、板厚、板长、面板模量、传力杆和排水能力作为与错台发展相关的设计特征.接缝状况采用不同接缝允许水分入渗率来表征,路肩传荷能力采用传荷系数来表征,路肩基层支撑能力采用路肩下基层顶面当量回弹模量与面板下基层顶面当量回弹模量的比值表征,基层冲刷采用抗冲刷等级进行表征,排水能力采用降雨量排除率来表征.

针对错台的设计特征，敏感性分析分为2个阶段.第1阶段为敏感性分析方法优选和最优设计特征确定.基于LTPP水泥混凝土路面错台数据,对比相关分析、灰色关联分析、神经网络方法、主成分分析法、方差分析等5种方法对敏感性分析效果,利用变异系数评价分析结果的离散程度,并结合图形分析进行验证,采用离散程度较大的分析方法进行下阶段的敏感性分析.第2阶段为采用优选的方法对基于最优设计特征分类后的数据库进行敏感性分析.结合较好分析方法所得的影响程度最大的设计特征—传力杆,将错台数据分为有传力杆和无传力杆数据集,采用相关分析和方差分析,分别开展设计特征敏感性分析,并结合图形分析进行验证,得到水泥混凝土路面设计特征的重要性排序,从设计层面提出抑制路面错台的建议.

2 敏感性分析方法

不同敏感性方法效果可能不相同,应结合各因素变量特点,选择合理的方法.相关分析、方差分析、图形分析已被用来分析错台影响因素的敏感性，灰色关联分析、主成分分析也被运用于分析路面性能影响因素的敏感性,神经网络亦用于研究影响因素重要度,均获得较好结果.因此,本研究结合以上6种方法开展研究.

2.1 相关分析法

相关分析法衡量的是2个变量因素的相关密切程度,本试验研究的是设计特征与错台量的相关程度.选择Spearman相关系数作为分析参数[12].错台样本点相对较少,且所分析的因素相对较多,所以采用的显著水平为0.1[13],认为显著性小于0.1时,影响因素的关联性为真.当显著性小于0.1,相关系数的绝对值越大,相关性越显著.

2.2 方差分析法

方差分析法是针对多个总体,在方差相同的条件下,检验其均值是否相等的一种统计方法,具体思路是将错台数据的总变差平方和拆分为因素的变差平方和与随机误差平方和之和,然后作F检验,即可求得设计特征作用的显著性[14].当显著性小于0.05时,F值越大,影响越显著[7].

2.3 灰色关联度分析法

灰色关联度分析法是分析系统中各因素关联程度的方法,即分析设计特征与错台值的关联程度.计算步骤如下[8]:先设一组离散序列,设错台为母因素序列,影响错台的设计特征为子因素序列;采用均值化方法对错台数据与设计特征作量纲归一化处理;根据公式计算关联系数和灰色关联度.灰色关联度ri构成的序列描述了各设计特征对错台的影响.灰色关联度越大,影响越强烈.

2.4 主成分分析法

主成分分析法首先需将原始指标数据标准化,然后按累计方差贡献率不低于某个值(取值为85%)的原则确定k个主成分,最后根据各成分贡献率计算得到设计特征的影响程度[9].影响程度wj可根据各成分贡献率计算得到,即

(1)

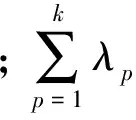
(2)

2.5 神经网络法

各设计特征作为输入变量进行BP神经网络分析,输出变量为错台量.选取49个路段153个样本点为训练集,12个路段39个数据作为检验集进行计算.所有原始数据在网络输入前均经过归一化处理转变为(0,1)区间的实数.通过训练BP神经网络,得到各设计特征与错台间的关系后,从神经网络中提取输入层到隐含层、隐含层到输出层之间的权值和阀值,结合Carson算法,进行多参数敏感性分析计算,得到不同影响因素对错台的贡献值.Carson算法是利用神经网络各层间连接权值进行敏感性分析的方法,基本原理是用连接权值的乘积来计算输入变量对输出变量的贡献程度.输入变量xi对输出变量Ot的影响程度[15]为

(3)

式中: 输入层、隐含层、输出层的单元数分别为n,p,q;vij为输入层至隐含层的连接权值,i=1,2,…,n,j=1,2,…,p;wjt为隐含层至输出层的连接权值,j=1,2,…,p,t=1,2,…,q.由于实际上连接权值的符号可正可负,为表达单一基本变量对整个网络的影响贡献,故在上式中连接权值均为绝对值.

2.6 图形分析法

图形分析法将离散型自变量的各种取值对应的因变量的均值绘成图表,直观观察多组样本间均值的变化,这种方法简单明了.对于不同自变量对应的因变量均值相差较大的情况下,可直观判断,但是对于均值接近的情况,判断精度相对较差,该方法可用于粗略比较,还可用来补充数学和统计方法的结果,使最终结果更为完整[2].利用图形分析的设计特征敏感性分析的基本思路如下:忽略其他设计特征,分别考虑各设计特征对错台的单一影响,定性得出较为重要的设计特征.

3 设计特征敏感性分析

3.1 方法对比

图1为采用相关分析、方差分析、灰色关联度分析、主成分分析、神经网络等5种方法进行设计特征敏感性分析的结果.由图1a,b可知,相关分析和方差分析都表明传力杆是影响错台最关键的设计特征,这与大多数的研究相一致[2-4].相关分析得到设计特征重要度由大到小排序为传力杆、排水能力、路肩传荷能力、基层冲刷系数和板厚.方差分析由大到小的排序为传力杆、板长、基层冲刷系数、路肩传荷能力、面板模量、路肩基层支撑能力和排水能力.除传力杆排序外,其他设计特征的排序并不一致,但均涉及了排水能力、路肩传荷能力、基层冲刷系数等普遍认为对错台影响较大的设计特征.另外3种方法难以体现传力杆对错台的重要作用,与大多研究结论并不相符.图1c表明灰色关联度分析结果中面板模量是影响错台的最重要设计特征,而传力杆直径的影响却最小.同时,10个设计特征的比值较为接近,难以区分其重要程度.这可能是由于灰色关联法都采用计算逐点关联测度平均值来确定关联度,平均值淹没了许多点关联测度的个性,可能造成信息损失[13].图1d显示主成分分析受到板长对错台的影响最大,传力杆的影响居中,且多个设计特征的影响相接近.这可能与主成分分析未考虑因素本身与分析目标的相对重要程度等相关[16].由图1e可知,神经网络法得到基层冲刷系数的影响最大,传力杆的影响并不明显,且其中很多因素的重要程度也相同或接近,难以体现敏感度.这可能与神经网络中神经元的连接权值的随机性造成了敏感性分析结果的不稳定性有关[17].同时,主成分分析与神经网络法均要求敏感性系数总和为1,但所涉及的影响因素较多,导致各因素敏感性系数的差异并不明显.因此,采用主成分分析与神经网络对涉及较多因素的分析有一定局限性.

图1 敏感性数值对比

不同方法分析效果也可用离散程度来评价.离散程度越高,分析效果越好.由于参数量纲不同,离散程度用变异系数Cv表示[17],即

(4)

式中:σx为随机变量标准差;μx为随机变量均值.

不同方法计算所得的变异系数分别如下:相关分析为0.75,方差分析为0.65,灰色关联分析为0.08,主成份分析为0.22,神经网络分析为0.20.这表明相关分析结果离散程度最大,分析效果最好,方差分析的效果次之,主成分分析与神经网络分析的变异系数均在0.20左右,分析效果在同一层次,而灰色关联分析的变异系数最小,分析效果最差.

3.2 方法验证

图2为基于图形法的不同设计特征对错台的影响.由图2可知：传力杆对错台有较强影响;表明路肩传荷能力、基层冲刷系数、排水对错台有一定影响,而其他设计特征(接缝状况、路肩基层支撑能力、地基复合模量、板厚、板长、面板模量)对错台的影响程度尚不明确;相关分析、方差分析结果均表明传力杆对错台的影响最大,这与基于实际数据的图形分析结果较相符.

图形分析表明路肩传荷能力、排水能力、基层冲刷系数对错台有影响,而相关分析、方差分析也得到了相似的结果.这说明了相关分析与方差分析具有一定的可靠性.

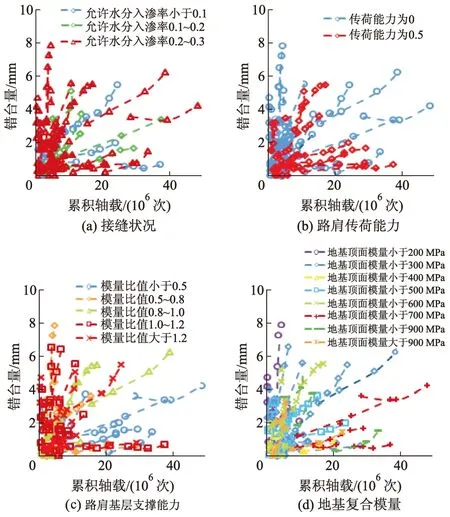
图2 基于图形法的不同设计特征对错台的影响

但相关分析得到的板厚和方差分析得到的板长、面板模量、路肩基层支撑能力对错台的影响,在图形分析结果中未能体现.这可能与传力杆对错台影响较大,受到各因素的交互作用等问题的影响,某些设计特征的重要性并不能体现.因此,可基于传力杆将数据集分为有传力杆和无传力杆数据集,从而减轻传力杆与其他设计特征的交互影响.

4 路面设计特征敏感性分析

基于相关分析与方差分析,将整个数据集分为有传力杆路面和无传力杆路面.有传力杆路面错台数据集包括23个有传力杆路段的73个样本点,而无传力杆路面错台数据集包括38个无传力杆路段的119个样本点.结合相关分析与方差分析法,分别研究不同设计特征对有/无传力杆水泥混凝土路面错台的影响.图3为有传力杆路面敏感性数值对比.由图3可知:对于有传力杆路面错台,基于相关分析的重要性由大到小排序为传力杆直径、板长和排水能力;基于方差分析，传力杆直径重要性大于排水能力.

图3 有传力杆路面敏感性数值对比

图4为基于图形法的不同设计特征对有传力杆路面错台的影响.由图4可知:传力杆、板长、排水能力有较大影响,这与相关分析结果一致;方差分析得到的重要设计特征也在图形分析中有所体现,只是板长的重要性尚不能在方差分析中得以体现.

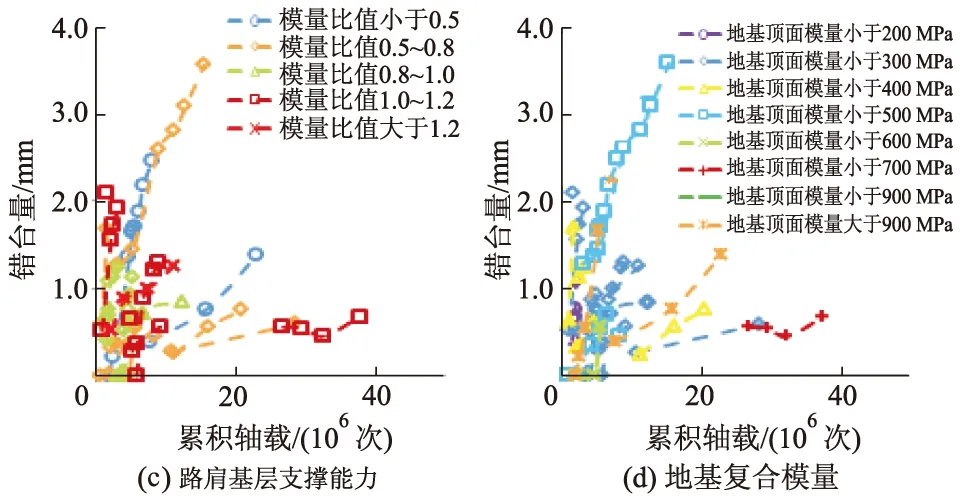
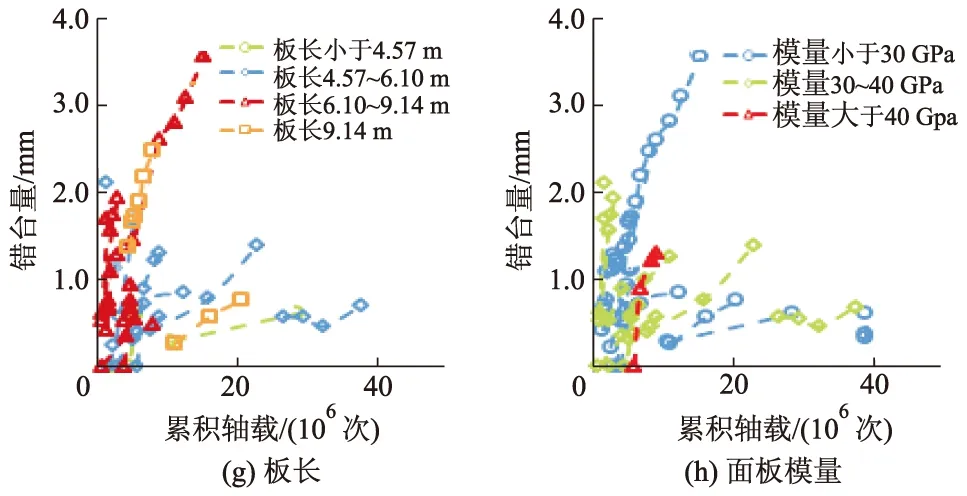
图4 基于图形法的不同设计特征对有传力杆路面错台的影响

图5为无传力杆路面敏感性数值对比.由图5可知:无传力杆时,基于相关分析的重要性由大到小排序为板长、排水能力、基层冲刷系数和路肩传荷能力;基于方差分析的由大到小重要性排序为路肩基层支撑能力、地基复合模量和面板模量.

图5 无传力杆路面敏感性数值对比

图6为基于图形法的不同设计特征对无传力杆路面错台的影响.由图6可知:路肩传荷能力、基层冲刷系数、板长、排水能力有较大影响,这与相关分析结果也相同;方差分析结果与图形分析结果并不一致.因此,采用相关分析对设计特征的敏感性进行分析较为正确.

由图1,3,5的分析结果可知:在未进行数据分类以前,板长对错台的影响并没有体现,但数据分类后,板长的影响得以体现,这与多数研究认为板长对错台有影响的结论相符[2,6-7];排水能力、基层冲刷系数、路肩传荷能力等设计特征都有所体现,这说明基于传力杆将数据进行分类是必要的.

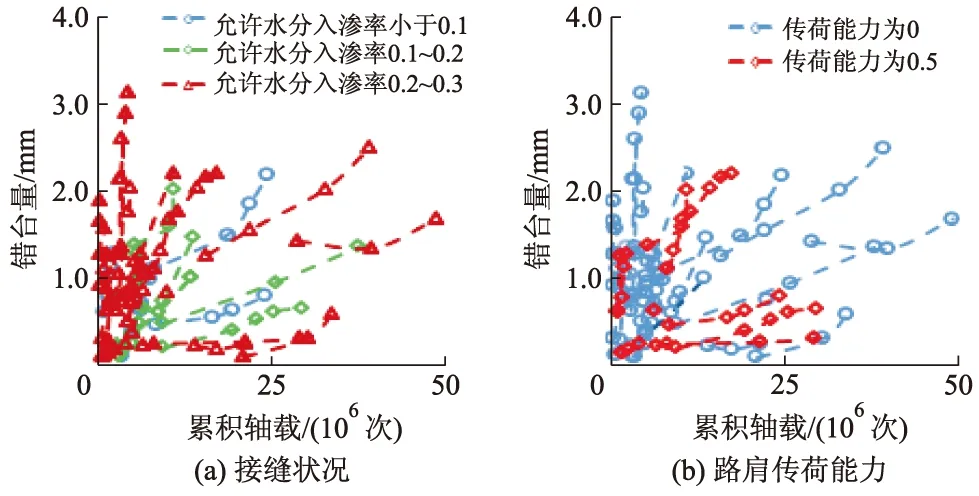
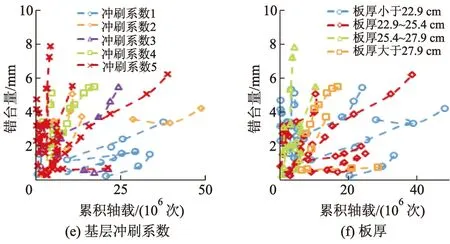
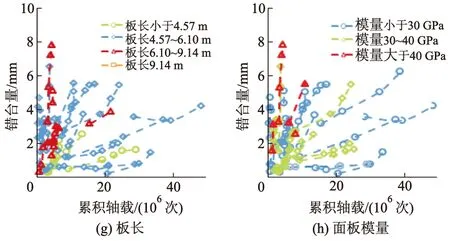
图6 基于图形法的不同设计特征对无传力杆路面错台的影响

综上,传力杆直径对有传力杆路面错台影响较大,板长对无传力杆路面错台影响较大.基于敏感性分析提出水泥混凝土路面错台抑制建议:传力杆是普通水泥混凝土路面最重要的设计特征,在设计时应重点考虑;针对有传力杆水泥混凝土路面,设置传力杆较有效,减小面板长度,设置排水系统也能抑制错台;针对无传力杆水泥混凝土路面,减小面板长度是最有效的措施,设置排水系统,考虑基层冲刷也可抑制错台.

5 结 论

1) 提出了基于路面性能实测数据的设计特征敏感性分析二阶段流程及数据分析框架.

2) 相关分析对现有错台数据有较好适应性,可采用相关分析进行设计特征敏感性分析;同时得到设计特征对不同类型路面的错台影响并不相同,有传力杆路面设计特征的重要性由大到小排序为传力杆直径、板长和排水能力,无传力杆路面设计特征的重要性由大到小排序为板长、排水能力、基层冲刷系数和路肩传荷能力.结合设计特征的重要性,提出了针对有/无传力杆水泥混凝土路面错台抑制建议.

3) 环境因素对错台也有较大影响,而本研究错台样本量较少,难以基于不同气候分区进行数据分类.所以在数据不断累积的情况下,可进一步分析不同气候分区下各设计特征对错台的影响.同时各影响因素交互作用对错台的影响也有待进一步研究.

)

[1] DERE Y, ASGARI A, SOTELINO E D, et al. Failure prediction of skewed jointed plain concrete pavements using 3d FE analysis[J]. Engineering Failure Analysis, 2006, 13: 898-913.

[2] 许鹰.基于生存分析理论的水泥混凝土路面服务寿命模型与大修时机研究[D].上海:同济大学,2012:99-119.

[3] JABLONSKI B, REGEHR J, REMPEL G. Guide for mechanistic-empirical design of new and rehabilitated pavement structures[R]∥Final Report Part Design Analysis. Washington, USA: Transportation Research Board National Research Council, 2001.

[4] BYRUM C R. Evaluating effectiveness of dowels in jointed-concrete pavements with faulting data from rapid-travel profilers[J]. Journal of the Transportation Research Board, 2010, 2154(1): 32-43.

[5] SMITH K D, PESHKIN D G, DARTER M I, et al. Performance of jointed concrete pavements, vol. II: evaluation and modification of concrete pavement design and analysis models[R]. Washington,USA: Department of Transportation, 1990.

[6] SIMPSON A L, RAUHUT J B, JORDAHL P R, et al. Sensitivity analysis for selected pavement distress[R]. Washington, USA: National Research Council, 1994.

[7] JUNG J S, OWUSU-ANTWI E B, AN J H. Analytical procedures for evaluating factors that affect joint faulting for jointed plain concrete pavements using the long-term pavement performance database[J]. Canada Journal of Civil Engineering, 2006, 33: 1279-1286.

[8] 周娟兰,郑木莲,袁海涛,等.设应力吸收层复合式路面动态响应灰关联分析[J].武汉理工大学学报,2014,36(12):66-71.

ZHOU J L, ZHENG M L, YUAN H T, et al. Dynamic response and grey relational analysis of composite pavement with stress absorbing layer[J]. Journal of Wuhan University of Technology, 2014, 36(12):66-71.(in Chinese)

[9] 王威娜,秦煜,支喜兰,等.沥青路面早期性能指标权重非线性集化研究[J].合肥工业大学学报(自然科学版),2016,39(6):801-806.

WANG W N, QIN Y, ZHI X L, et al. Non-linear combination method of index weights for evaluation of asphalt pavement initial performance[J]. Journal of Hefei University of Technology, 2016,39(6):801-806. (in Chinese)

[10] 蔡毅,邢岩,胡丹.敏感性分析综述[J].北京师范大学学报(自然科学版),2008,44(1):9-16.

CAI Y, XING Y, HU D. On sensitivity analysis[J]. Journal of Beijing Normal University (Natural Science), 2008, 44(1):9-16. (in Chinese)

[11] ELKINS G E, SCHMALZER P, THOMPSON T, et al. Long-term pavement performance information management system: pavement performance database user re-ference guide[R]. Washington, USA: National Research Council, 2010.

[12] 李峰,黄颂昌,徐剑.沥青路面加热型密封胶的性能评价[J].同济大学学报(自然科学版),2013,41(8):1208-1212.

LI F,HUANG S C,XU J. Performance evaluation of asphalt pavement hot-applied sealant[J]. Journal of Tongji University (Natural Science), 2013, 41(8):1208-1212. (in Chinese)

[13] 盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社,2008.

[14] 陈鹏,徐博侯.基于因素敏感性的边坡稳定可靠度分析[J].中国公路学报,2012,25(4):42-48.

CHEN P, XU B H. Reliability analysis of slope stability based on factors sensitivity[J]. China Journal of Highway and Transport, 2012, 25(4):42-48.(in Chinese)

[15] 陈志强,郭子瑞,窦克忠,等.基于BP神经网络的污泥水解液合成PHA的多参数敏感性分析[J].环境科学学报,2013,33(12):3244-3250.

CHEN Z Q, GUO Z R, DOU K Z, et al. Multi-parameter sensitivity analysis of polyhydroxyalkanoate (PHA) production utilizing sludge hydrolysis liquid based on BP neural network method[J]. Acta Scientiae Circumstan-tiae, 2013, 33(12): 3244-3250. (in Chinese)

[16] VISCONTI F, DE PAZ J M, RUBIO J L. Principal component analysis of chemical properties of soil saturation extracts from an irrigated mediterranean area: implications for calcite equilibrium in soil solutions[J]. Geoderma, 2009, 151(3): 407-416.

[17] FREY H C, PATIL S R. Identification and review of sensitivity analysis methods[J]. Risk Analysis, 2002, 22(3): 553-578.