有限分布源与瞬时源浓度分布计算的分类准则

武周虎

（青岛理工大学 环境与市政工程学院，山东 青岛 266033）

1 研究背景

有毒有害物质进入水环境的途径包括事故直接导致和事故处理处置过程的间接导致，污染物进入水体的排放方式一般包括“瞬时源”、“有限时段源”和“起始有限分布源”。在《环境水力学》［1-3］中，从瞬时平面源一维扩散浓度分布的解析解出发，依次得到了瞬时线源二维扩散和瞬时点源三维扩散浓度分布的解析解以及一、二、三维起始有限分布源相应的一、二、三维扩散浓度分布的解析解。

张江山［4-5］在瞬时点源条件下探讨了三维超标污染区域的几何特征及最大超标范围，并通过瞬时线源二维示踪实验给出了确定河流纵向离散系数和横向混合系数的线性回归法，但对瞬时点源和线源的适用条件未作讨论。武周虎［6］在求解了有限时段源一维水质模型方程解析解的基础上，提出了将“有限时段源”简化为“瞬时排放源”的判别条件，定义并给出了“无量纲数”的定量判据，解决了多年来困扰环境水力学学术界“瞬时源”排放时间的相对长短问题。但仍缺乏一、二、三维起始有限分布源与瞬时平面源、线源、点源的分类准则，给水环境影响预测计算公式的选择带来困难［7］。在数学上，平面源、线源和点源依次是没有厚度、粗细和大小的。但在污染物扩散计算中，通常需要假设在有限分布源的空间尺度相对于污染物扩散计算的空间尺度很小时，可近似按平面源或线源或点源来处理。尚缺乏定量的判据和误差控制范围，给教学过程和实际工作带来不便。

本文从一、二、三维起始有限分布源和瞬时平面源、线源、点源相应维度扩散浓度分布的解析解出发，通过相应维度扩散浓度分布及其特性分析与比较，提出一、二、三维起始有限分布源分别简化为瞬时平面源、线源、点源的临界条件，给出相应的污染源分类准则，为建设项目水环境风险影响预测与评价以及增强《环境风险防范措施和环境风险应急预案》的可靠性，提供理论支持。

2 一维起始有限分布源与瞬时平面源的分类准则

2.1一维扩散浓度分布分析与比较设在一维无限长的清水环境中，有一段起始浓度均匀、分布长度为2a的有限分布源。坐标原点O设在有限分布源的中心处，取x轴与一维水体的轴线平行，如图1所示。

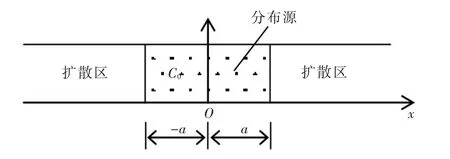
图1 一维起始有限分布源示意

一维起始有限分布源扩散污染物的浓度分布为［1-2］：

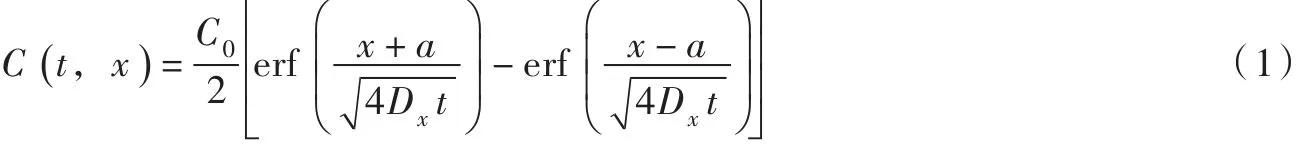
式中：C(t，x)为t时间x处的污染物浓度；C0为有限分布源的起始污染物浓度；Dx为x方向的扩散系数。浓度单位为mg/L，其它参数和自变量采用m-s单位制。

瞬时平面源一维扩散污染物的浓度分布为［1-2］：

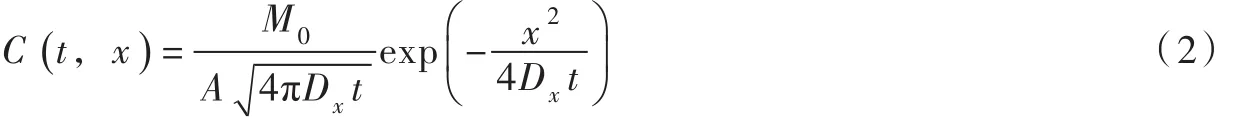
式中：M0为t=0时间x=0处瞬时平面源的污染物总排放量；A为一维水体的断面面积；其它符号同前。取M0等于一维起始有限分布源的污染物总排放量2aAC0，代入式（2）变为：

为了便于分析与比较，对式（1）和式（3）作无量纲处理。令污染物的相对浓度C′=C/C0；无量纲纵向坐标 x′=x/2a。定义：无量纲数（即：Wu’s数），对一维问题，Wu=Wux。表示起始有限分布源的长度2a与t时间、x方向浓度分布的特征长度（）比值。为t时间浓度分布的标准差，最大浓度两侧区间对应浓度分布曲线与x轴所围面积占总面积的比例为52.05%。

将以上无量纲参数代入式（1）整理得到一维起始有限分布源扩散的相对浓度分布为：

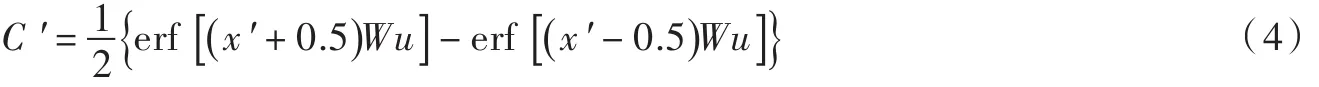
将以上无量纲参数代入式（3）整理得到瞬时平面源一维扩散的相对浓度分布为：

在一维有限分布源的长度和扩散系数不变的条件下，无量纲数Wu仅与t-0.5成正比，即Wu随扩散时间的增大迅速减小。在污染源排放的初始时间t=0，相应的Wu=∞。给定一系列无量纲数Wu=5.0，2.0，1.0，0.5，由式（4）和式（5）分别计算一维起始有限分布源与瞬时平面源一维扩散的相对浓度分布，点绘于图2进行比较.

由图2（a）看出，一维起始有限分布源的扩散受起始浓度分布长度的直接作用，在扩散时间较小、无量纲数Wu较大时，相对浓度分布呈矮胖型，中间出现平顶段，最大相对浓度等于1；随着扩散时间的增大，无量纲数Wu迅速减小，浓度分布曲线的中间平顶段消失，最大相对浓度逐步下降，污染物的分布范围逐渐扩大。由图2（b）看出，对污染物总排放量相同的瞬时平面源的一维扩散而言，在扩散时间较小、无量纲数Wu较大时，相对浓度分布呈瘦高型，最大相对浓度远大于1，污染物主要集中在最大值附近；随着扩散时间的增大，无量纲数Wu迅速减小，最大相对浓度迅速下降，污染物的分布范围迅速扩大。

图2 一维扩散的相对浓度分布比较

由图2（a）（b）比较看出，随着扩散时间的进一步增大，当无量纲数Wu减小到小于1时，一维起始有限分布源与瞬时平面源一维扩散的最大相对浓度和相对浓度分布逐步趋于一致。在文献［8］中，瞬时平面源一维扩散的浓度分布图3-3和一维起始有限分布源扩散的浓度分布图3-5，在扩散时间t较小时的分布曲线绘制明显错误；在有边界反射的扩散浓度分布图3-6和图3-7中出现明显不满足边界条件的情况。

2.2一维起始有限分布源简化为瞬时平面源的判据将x′=0代入式（4）得到扩散时间t、相应无量纲数Wu条件下，一维起始有限分布源扩散的最大相对浓度为：

将x′=0代入式（5）得到扩散时间t、相应无量纲数Wu条件下，瞬时平面源一维扩散的最大相对浓度为：

由式（7）和式（6）得到扩散时间t、相应无量纲数Wu条件下，瞬时平面源与起始有限分布源扩散的最大浓度比值为：

由式（6）—（8）看出，一维起始有限分布源与瞬时平面源一维扩散的最大相对浓度以及它们的比值，仅与无量纲数Wu有关，瞬时平面源一维扩散的最大相对浓度与Wu呈线性增长关系。图3给出了瞬时平面源一维扩散的最大相对浓度C′m、一维起始有限分布源扩散的最大相对浓度C′m1以及它们的比值函数f（Wu）与无量纲数Wu的变化关系。

图3 有限分布源、瞬时平面源的最大浓度及其比值与Wu的关系

由图3看出，一维起始有限分布源扩散的最大相对浓度C′m1随Wu呈单调递增关系，其值在Wu＞3时很快趋近于极大值1，而当Wu减小到小于1时，则以瞬时平面源一维扩散的最大相对浓度为渐近线。最大浓度的比值函数f（Wu）随Wu呈单调递增关系，当Wu→0时，f（Wu）→1。也就是说，当扩散时间较大、Wu→0时，一维起始有限分布源与瞬时平面源扩散的最大浓度值有一个渐近过程。

据此定义：将瞬时平面源与起始有限分布源扩散的最大浓度比值等于1.05，作为一维起始有限分布源可以简化为瞬时平面源一维扩散的分类临界条件。由式（8）和图3不难得到，一维起始有限分布源与瞬时平面源扩散的无量纲临界判据为：

那么，一维起始有限分布源简化为瞬时平面源扩散的判别条件为：

或者：

2.3一维分类临界状态的浓度分布比较及其标准差分析将无量纲临界判据Wuk1=0.77代入式（4）和式（5）分别计算一维起始有限分布源和瞬时平面源一维扩散的相对浓度分布，点绘于图4。

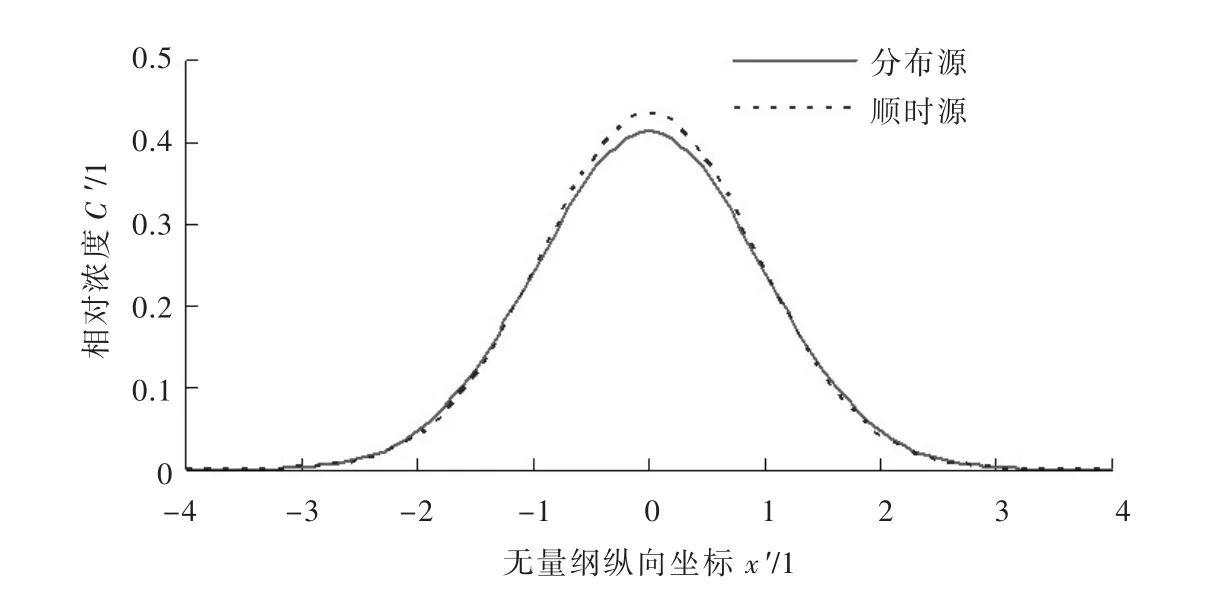
图4 在临界状态时，有限分布源与瞬时平面源的浓度分布比较

由图4看出，在分类临界状态时，一维起始有限分布源与瞬时平面源扩散的相对浓度分布特征、规律和变化趋势完全一致。前者分布源的最大相对浓度为0.4139，后者瞬时源的最大相对浓度为0.4344，两者的相对误差为5.0%。瞬时平面源一维扩散相对浓度分布（正态分布）的标准差；采用数值积分法计算一维起始有限分布源扩散相对浓度分布的标准差为0.9639，两者标准差的相对误差为-4.7%。说明采用瞬时平面源与起始有限分布源扩散最大浓度相对误差5.0%确定的分类临界条件，同时也满足两者浓度分布标准差的相对误差绝对值小于5.0%的要求。

根据浓度分布特性，峰值点两侧对称区间分布宽度4σx′范围内的污染物质量占总排放量的95.5%。因此，在临界状态时，污染物的分布宽度是一维起始有限分布源长度2a的4σx′=3.67倍。由图3可知，随着扩散历时的进一步增大，无量纲数Wu不断减小，两者计算结果的相对误差将进一步减小，相对浓度分布曲线和特性的吻合程度将进一步提高。

3 二维起始有限分布源与瞬时线源的分类准则

3.1二维扩散浓度分布分析设在二维无限域清水环境中，有一起始浓度均匀、分布面积为长×宽=2a×2b的有限分布源。坐标原点O设在有限分布源的中心点，取x、y轴分别与2a长边和2b宽边平行，如图5所示。垂直于XOY平面为无限延伸或等水深“柱状源”或“线源”条件，下面按单位水深进行分析。

二维起始有限分布源扩散污染物的浓度分布为［1-2］

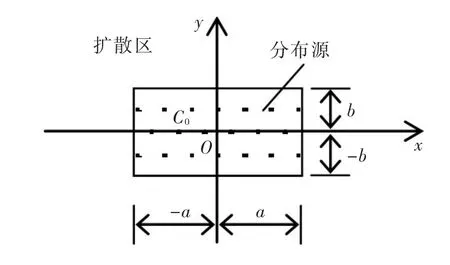
图5 二维起始有限分布源示意图

式中：C（t，x，y）为t时间、（x，y）点的污染物浓度；C0为有限分布源的起始污染物浓度；Dx、Dy分别为x、y方向的扩散系数。

瞬时线源二维扩散污染物的浓度分布为［1-2］：

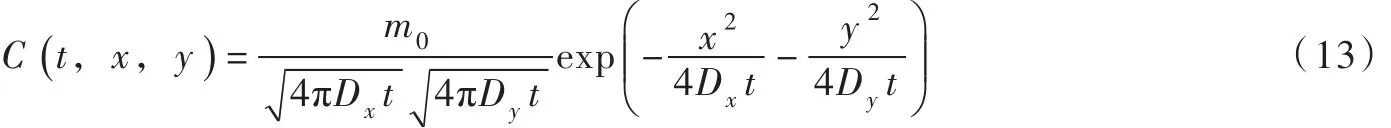
式中：m0为t=0时间、（x=y=0）点单位水深上瞬时线源的污染物总排放量。取m0等于二维起始有限分布源单位水深上的污染物总排放量（2a×2b）C0，代入式（13）变为：

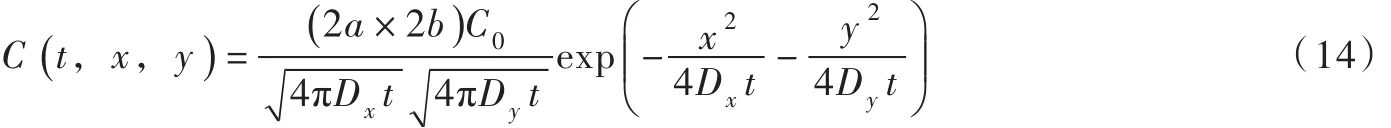
将以上无量纲参数代入式（12）整理得到二维起始有限分布源扩散的相对浓度分布为：

将以上无量纲参数代入式（14）整理得到瞬时线源二维扩散的相对浓度分布为：

在二维有限分布源的长度、宽度和扩散系数不变的条件下，无量纲数Wux和Wuy仅与t-0.5成正比，即Wux和Wuy随扩散时间的增大迅速减小。对不同的扩散时间t，计算无量纲数Wux和Wuy，由式（15）和式（16）分别绘制x、y坐标轴上二维起始有限分布源与瞬时线源二维扩散的相对浓度分布曲线进行比较，其情况类似于图2（a）（b）的比较，分析从略。

3.2二维起始有限分布源简化为瞬时线源的判据将 x′=y′=0代入式（16）和式（15）分别得到扩散时间t、相应无量纲数Wux和Wuy条件下，瞬时线源与二维起始有限分布源扩散的最大相对浓度。两者相除，可以得到瞬时线源与二维起始有限分布源扩散的最大浓度比值为：

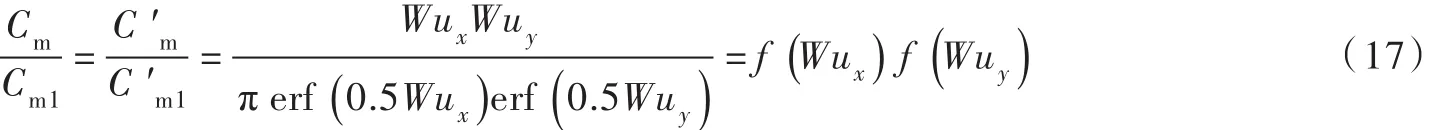
由图3可知，函数 f(Wu)随Wu呈单调递增关系，当Wu→0时， f(Wu)→1。为了获得瞬时线源与二维起始有限分布源扩散最大浓度相对误差5%的分类临界条件，假设：

据此，由式（17）得到瞬时线源与二维起始有限分布源扩散的最大浓度比值为：

说明将满足式（18）条件的无量纲数Wuk2，作为二维起始有限分布源可以简化为瞬时线源二维扩散的分类临界条件，可实现瞬时线源与起始有限分布源扩散最大浓度的最大相对误差范围为2.5%～5.1%。根据式（18）的条件，由图3和式（8）得到二维起始有限分布源与瞬时线源扩散的无量纲临界判据为：

那么，二维起始有限分布源简化为瞬时线源扩散的判别条件为：

或者：

由式（22）看出，二维起始有限分布源简化为瞬时线源扩散的判别条件取决于x或y坐标方向的有限分布源长度平方与相应方向的扩散系数之比。对天然河流，纵向离散系数和横向混合系数参照文献［9-10］中给出的方法确定。

3.3二维分类临界状态坐标轴上的浓度分布比较及其标准差分析将无量纲临界判据Wuk2=0.55（=Wux=Wuy）代入式（15）和式（16）分别计算x、y坐标轴上二维起始有限分布源和瞬时线源二维扩散的相对浓度分布，垂向坐标按25×C′值点绘于图6。

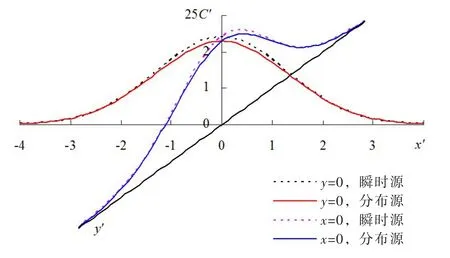
图6 在临界状态时，有限分布源与瞬时线源的浓度分布比较

由图6看出，在分类临界状态时，二维起始有限分布源与瞬时线源扩散的相对浓度分布特征、规律和变化趋势完全一致。前者分布源的最大相对浓度为0.0916，后者瞬时源的最大相对浓度为0.0963，两者的相对误差为5.1%。在x轴（y=0）上，瞬时线源二维扩散相对浓度分布（正态分布）的标准差；采用数值积分法计算二维起始有限分布源扩散相对浓度分布的标准差为1.3186，两者标准差的相对误差为-2.5%。表明，在最大浓度的相对误差5.0%条件下，二维比一维扩散相对浓度分布标准差的相对误差绝对值更小。

由于采用无量纲数Wux和Wuy同时满足临界判据Wuk2=0.55的条件，所以，在y轴（x=0）上，二维扩散相对浓度分布与x轴上的相同，分析从略。在x、y轴上，污染物的分布宽度是二维起始有限分布源相同方向长度的4σ′=5.14倍。

4 三维起始有限分布源与瞬时点源的分类准则

4.1三维扩散浓度分布分析三维起始有限分布源，又称为瞬时有限体积源。设在三维无限域清水环境中，有一起始浓度均匀、分布体积为长×宽×高=2a×2b×2d的有限体积源。坐标原点O设在有限体积源的中心点，取x、y、z轴分别与2a长边、2b宽边、2d高边平行。

三维起始有限分布源扩散污染物的浓度分布为［1-2］：

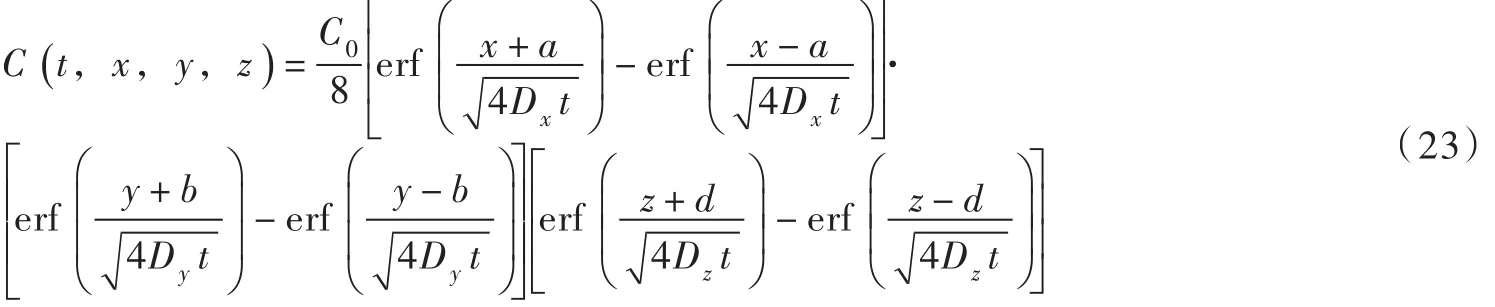
式中：C（t，x，y，z）为t时间、（x，y，z）点的污染物浓度；C0为有限体积源的起始污染物浓度；Dx、Dy、Dz分别为x、y、z方向的扩散系数。

瞬时点源三维扩散污染物的浓度分布为［1-2］：

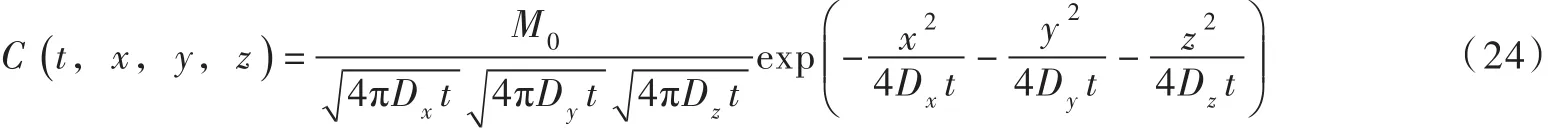
式中：M0为t=0时间、（x=y=z=0）点瞬时点源的污染物总排放量。取M0等于三维起始有限分布源的污染物总排放量（2a×2b×2d）C0，代入式（24）变为：

将以上无量纲参数代入式（23），并令x′=y′=z′=0，整理得到三维起始有限分布源扩散的最大相对浓度为：

将以上无量纲参数代入式（25），并令 x′=y′=z′=0，整理得到瞬时点源三维扩散的最大相对浓度为：

在三维有限分布源的长度、宽度、高度和扩散系数不变的条件下，无量纲数Wux、Wuy和Wuz仅与t-0.5成正比，即Wux、Wuy和Wuz随扩散时间的增大迅速减小。对不同的扩散时间t，计算无量纲数Wux、Wuy和Wuz，由式（26）和式（27）分别得到瞬时有限体积源和瞬时点源三维扩散的最大相对浓度进行比较，关于三维浓度分布的分析比较从略。

4.2三维起始有限分布源简化为瞬时点源的判据由式（27）与式（26）相除，可以得到瞬时点源与三维起始有限分布源扩散的最大浓度比值为：

为了获得瞬时点源与三维起始有限分布源扩散最大浓度相对误差5%的分类临界条件，假设：

据此，由式（28）得到瞬时点源与三维起始有限分布源扩散的最大浓度比值为：

说明将满足式（29）条件的无量纲数Wuk3，作为三维起始有限分布源可以简化为瞬时点源三维扩散的分类临界条件，可实现瞬时点源与起始有限分布源扩散最大浓度的最大相对误差范围为1.6%～4.9%。根据式（29）的条件，由图3和式（8）得到三维起始有限分布源与瞬时点源扩散的无量纲临界判据为：

那么，三维起始有限分布源简化为瞬时点源扩散的判别条件为：

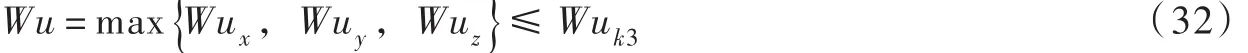
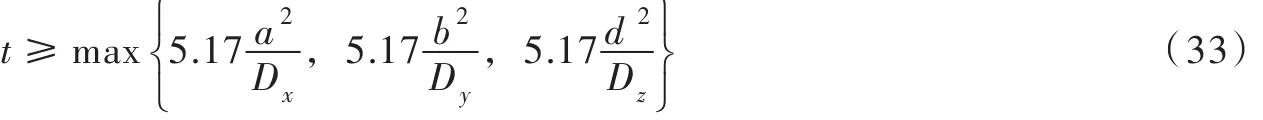
或者：

4.3三维分类临界状态最大浓度与坐标轴上浓度分布的标准差分析将无量纲临界判据Wuk3=0.44（=Wux=Wuy=Wuz）代入式（26）和式（27）得到三维起始有限分布源和瞬时点源扩散的最大相对浓度分别为0.0146和0.0153，两者的相对误差为4.9%。在x轴（y=z=0）上，瞬时点源三维扩散相对浓度分布（正态分布）的标准差。在最大浓度的相对误差5.0%条件下，三维比二维和一维扩散相对浓度分布标准差的相对误差绝对值更小。

由于采用无量纲数Wux、Wuy和Wuz同时满足临界判据Wuk3=0.44的条件，所以，在y轴和z轴上，三维扩散相对浓度分布与x轴上的相同，分析从略。在x、y、z轴上，污染物的分布宽度是三维起始有限分布源相同方向长度的4σ′=6.43倍。

值得一提的是，在水环境影响预测中，扩散时间t往往以“小时”或“天”进行计算，其扩散时间的“秒”数值一般较大。因此，起始有限分布源简化为瞬时平面源、线源、点源扩散的判别条件式（11）、式（22）和式（33）还是比较容易得到满足的，其分类准则具有很好的应用前景。

5 结论

（1）从一、二、三维起始有限分布源和瞬时平面源、线源、点源相应维度扩散浓度分布的解析解出发，提出了以起始有限分布源与相应维度瞬时源扩散的最大浓度相对误差5.0%作为分类临界点。研究表明，分类临界状态的浓度分布标准差的相对误差绝对值小于5.0%。（2）定义了Wu’s数分别给出了一、二、三维起始有限分布源与瞬时平面源、线源、点源分类的临界Wu’s数Wuk1=0.77、Wuk2=0.55、Wuk3=0.44。（3）给出了一、二、三维起始有限分布源分别简化为瞬时平面源、线源、点源扩散的判别条件：Wu=Wux≤Wuk1、和否则，应按相应维度起始有限分布源的扩散计算污染物浓度分布。（4）提出的各维度污染源分类准则，同样适用于非保守物质和移流扩散问题的污染源分类。

［1］FISCHER H B，IMBERGER J，LIST E J，et al.Mixing in Inland and Coastal Waters［M］.New York：Academic Press，1979.

［2］赵文谦.环境水力学［M］.成都：成都科技大学出版社，1986.

［3］张书农.环境水力学［M］.南京：河海大学出版社，1988.

［4］张江山.瞬时点源三维超标污染区域的几何特征及最大超标范围的估计［J］.中国环境科学，1997，17（6）：508-511.

［5］张江山.瞬时源示踪实验确定河流纵向离散系数和横向混合系数的线性回归法［J］.环境科学，1991，12（6）：40-43，63.

［6］武周虎.有限时段源一维水质模型的求解及其简化条件［J］.中国水利水电科学研究院学报，2017，15（5）：397-408.

［7］HJ 169－2016，中华人民共和国国家环境保护标准·建设项目环境风险评价技术导则［S］.北京：中华人民共和国环境保护部，2016.

［8］杨志峰，王烜，孙涛，等.环境水力学原理［M］.北京：北京师范大学出版社，2006.

［9］顾莉，华祖林.天然河流纵向离散系数确定方法的研究进展［J］.水利水电科技进展，2007，27（2）：85-89.

［10］顾莉，惠慧，华祖林，等.河流横向混合系数的研究进展［J］.水利学报，2014，45（4）：450-457，466.