产流误差平稳矩阵的系统响应修正方法参数分析

刘可新，李 匡，梁犁丽，徐海卿，柳 俊，赵培根

（中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038）

1 研究背景

世界范围内，洪水灾害正逐步加剧，就伤亡人数和经济损失而言，洪水灾害已位于自然灾害的前列［1］。同样，洪水灾害在我国也频繁发生，威胁着我国人民生命财产安全，据统计，在造成损失的自然灾害中，洪水稳居首位，对我国经济造成重大损失［2］。近年来，随着生态问题的不断加剧，极端天气的频次也与日俱增，洪水问题已成为制约我国经济发展的重要因素之一。洪水预报是防洪的主要非工程措施之一，其作用日益凸显，因此不断受到人们的重视［3］。由于水文规律的复杂性，洪水预报误差难以避免，有时甚至达不到精度要求，无法满足人民生产和生活的需要，因此一种可行有效的洪水预报误差修正方法十分必要，但现有的误差修正方法存在不少缺点，有些物理基础不强，有些不能保证预见期，整体上修正效果不理想。如传统的自回归模型［4-5］，假设误差系列存在相关性，在洪峰附近效果时常并不理想。再如卡尔曼滤波技术［6-8］，设计思路与理论基础都比较科学，但用在水文预报中，由于利用的实时信息量有限且有效信息获取困难，效果往往与自回归方法相近，这在很大程度上影响了洪水预报精度，难以达到防洪要求。

为提高实时洪水预报的精度，另辟蹊径，避免传统修正方法的缺陷，2012年，包为民等［9］在“基于单位线反演的产流误差修正”将单位线引入实时洪水预报修正中，建立一种向信息源头追溯的反馈修正模型，实质上建立了线性系统的系统响应修正方法，该方法不增加任何参数，结构十分简单，不损失预见期，且物理概念清晰。2013年，包为民等［10-11］提出了产流误差的动态系统响应曲线修正方法（以下简称DSRC方法），使系统响应修正方法由线性时不变系统扩展到非线性动态系统，以系统的线性化为手段，解决了复杂非线性系统的反演问题，为以后方法的应用奠定了坚实的基础，DSRC方法用流量预报误差作为修正信息来源，根据最小二乘法反演各时段计算产流的修正值，从而达到修正的效果。此后，系统响应修正方法得到了进一步的研究与探讨［12-19］。通过不断研究与应用，发现DSRC方法存在修正结果不稳定的问题，为解决这一问题，包为民等［20］提出了产流误差平稳矩阵的系统响应修正方法（以下简称RESM方法），扩展了系统响应修正方法的应用方位，增强了方法的修正稳定性，为系统响应修正方法应用于实际奠定了基础。

RESM方法虽然在理论上解决了DSRC方法修正结果不稳定的问题，但其中的参数尚需研究，以利于方法的推广应用。本文分别构建了理想案例和实际案例，对RESM方法的权重系数做了深入研究，并得到了相关结论，为今后方法的应用做准备。

2 RESM方法简介

RESM方法是在产流误差系统响应修正方法的基础上增添了稳定约束项，通过引入产流误差平稳矩阵，使无约束最小二乘法转变为约束最小二乘法，使时段产流修正值相互制约、相互联系，缓解或避免了大小相间的“震荡”现象，增强了修正结果的稳定性。最后应用动态系统响应理论，反演计算出较稳定的产流修正系列，对时段产流进行修正，该方法中权重系数的确定十分重要，影响着修正稳定性及修正效果。RESM方法的计算过程如下：

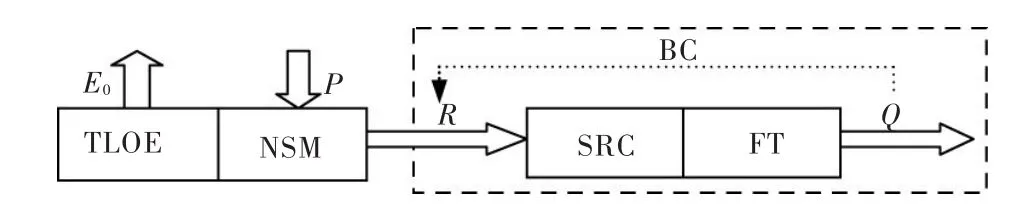
图1 新安江模型产流修正系统示意

图1是新安江模型示意图，其中E0表示实际蒸散发，P表示降雨，R表示产流量，Q表示出口流量，TLOE表示三层蒸发，NSM表示蓄满产流，SRC表示分水源，FT表示汇流，BC表示反演计算，虚线框中的部分表示系统。

只考虑产流对出口流量的影响，那么图1所示系统可以表示为式（1）：

式（1）的微分表达式为：

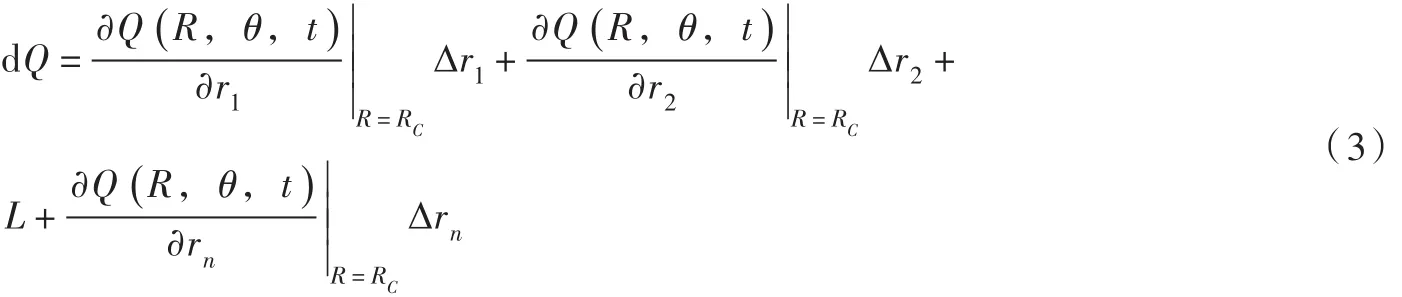
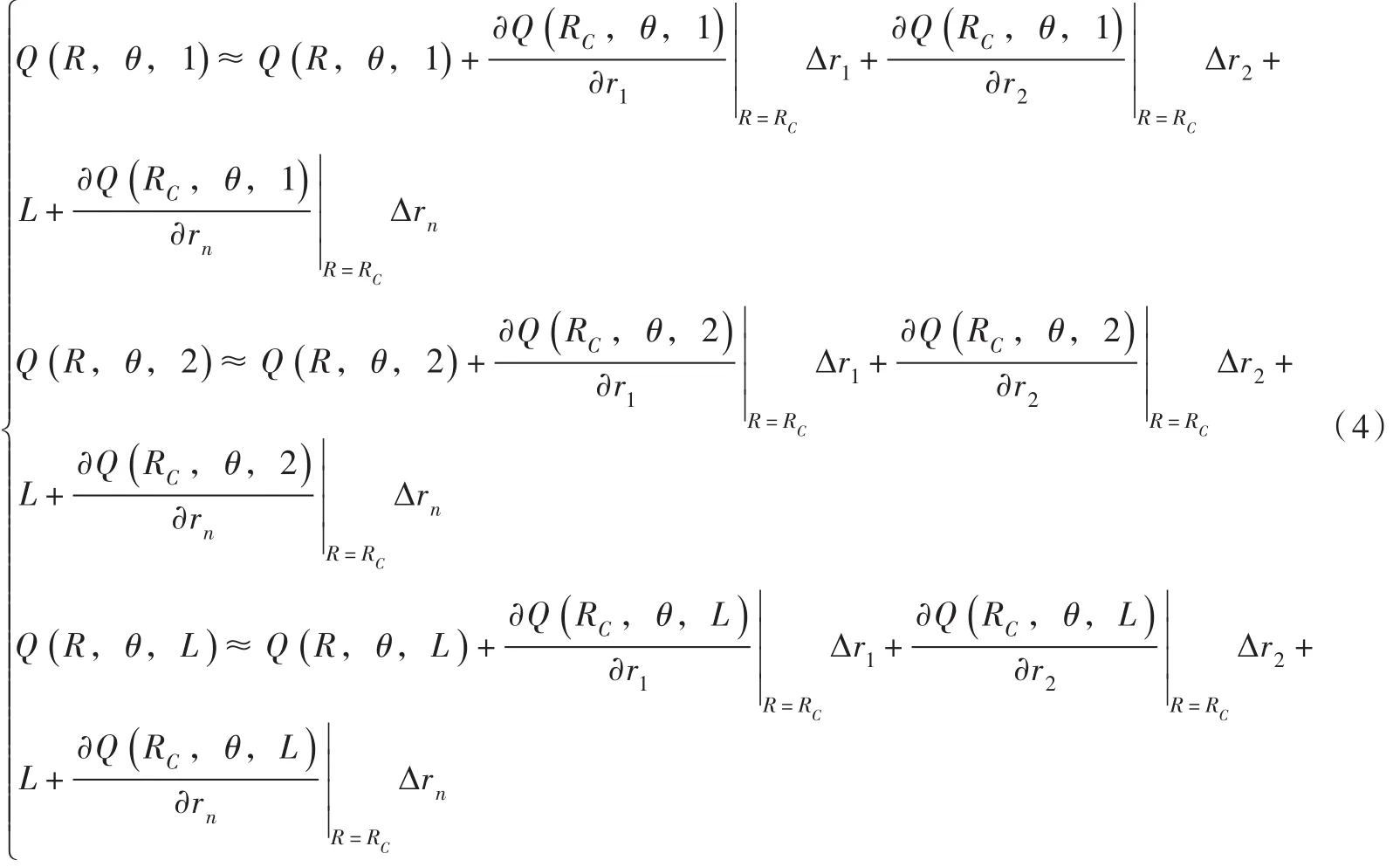
将式（4）写成矩阵形式，建立产流与流量之间的关系，可用式（5）表示：

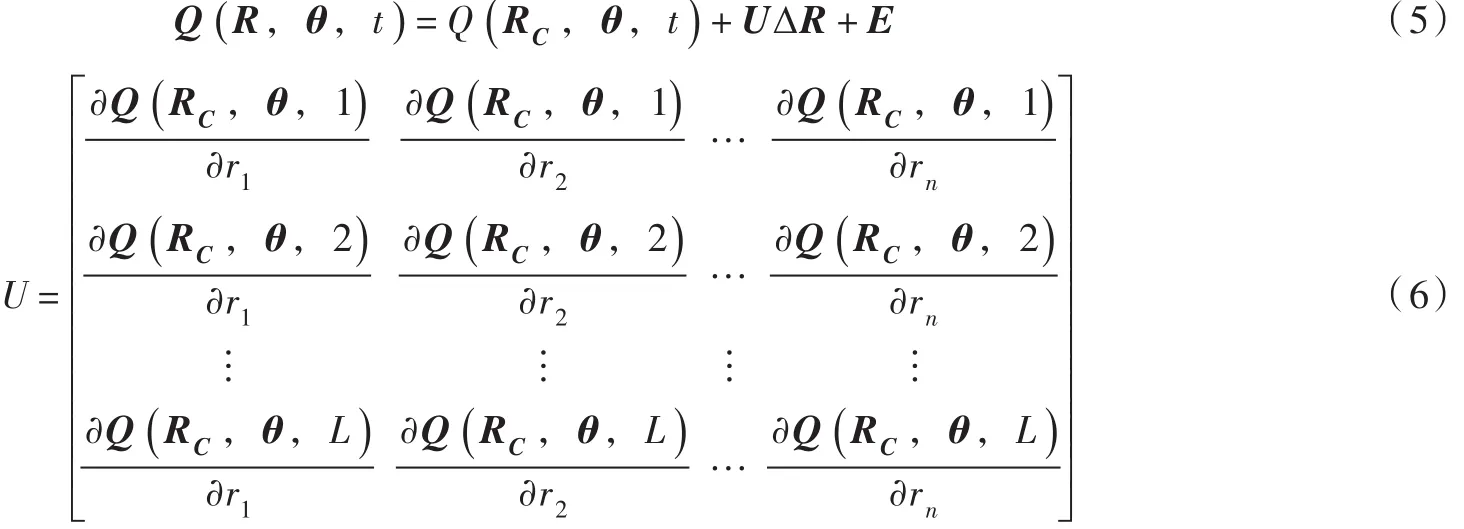
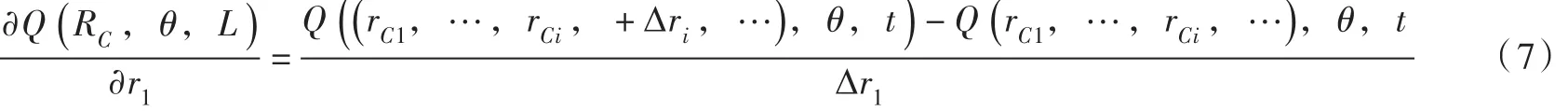
DSRC方法是根据无约束最小二乘原理，所求ΔR满足式（8）：

求解式（8）得：

修正后计算产流系列R′C为：

将R′C代入模型重新计算出流过程：

式中：Q′为修正后的计算流量系列。

在DSRC方法的基础上提出的RESM方法，将无约束最小二乘法替换为约束最小二乘法，在式（8）中加入稳定约束项，使时段产流修正值相互制约、相互联系，缓解或避免了大小相间的“震荡”现象，增强了修正结果的稳定性。方法及推导过程如下：

那么

在式（8）中加入稳定约束项，即ΔR满足：

式中：β为权重系数。

式（13）的值由两部分组成，稳定约束项和误差平方和项，其中误差平方和项主要作用是判断修正后流量过程线与实测流量过程线的接近程度，其值越小表示越接近，但该项无法考虑修正后时段产流结果是否稳定；而稳定约束项用于保证修正结果的稳定性，由式（13）容易看出，各时段产流修正比重越接近，其值越小，表示修正结果越稳定；反之，其值越大，表示越不稳定。权重系数β的作用是平衡稳定约束项与误差平方和项，不同洪水β值应不同。当β值为0时，RESM方法转化为DSRC方法，也就是说DSRC方法是RESM方法的特殊情况。稳定约束项与误差平方和项相互制约、相互联系、相互作用，使RESM方法既能保证稳定性，又能进一步改善修正效果。

求解式（13）得：

修正后计算产流系列R′C为：

将R′C代入模型重新计算出流过程：

式中：Q′为修正后的计算流量系列。

RESM方法依据系统响应理论，在DSRC方法的基础上改进而成，具有较强的物理基础，其中的产流系统响应曲线是指流域系统出口流量固有的对产流量的响应，是该方法具有物理基础的具体体现。

RESM方法能否达到预期的修正效果，关键是权重系数的选取，本文分别构建了理想案例和实际案例对权重系数进行较详细的分析。

3 RESM方法应用效果及权重系数的分析

为验证方法的修正效果，选取了以下5个洪水指标：

（1）洪量相对误差

（2）洪峰相对误差

（3）Nash-Sutcliffe系数

（4）时段产流修正比重

（5）平均产流修正比重

C的时段数；m为修正的产流时段个数；QCP为计算洪峰；QP为实测洪峰；RCT为计算次洪径流深；RT为实测径流深；NS系数表示修正的相对有效性，方法修正效果越好其值越大，最大值为1；ri为第i时段产流量；r′i为修正后第i时段产流量；m为修正的产流时段个数；Zi表示第i时段产流被修正程度的大小，其绝对值越大表示相对修正幅度越大；-Z是时段产流修正比重的均值，能够表示各时段产流的综合修正程度，其值越大表示修正结果相对越不稳定。

3.1理想案例分析理想案例中，流域面积为3 300 km2，区域中有10个雨量站，1个流量站，模型输入、输出、参数即中间变量均为已知量，给定产流真值系列R，代入模型得实测流量Q，随机生成一个误差系列ΔRT，产流真值系列R加上误差系列作为计算产流系列RC，代入模型得计算流量RC，误差限制条件是各误差不超30%。

同一场洪水，产流修正时段数和修正所用真值流量数一定的情况下，探讨权重系数、观察洪水修正效果、修正稳定性的变化。应用效果见表1、图2、图3。

表1数据显示，权重系数无论取多少，RESM方法均具有一定的修正效果，洪峰相对误差与洪量相对误差减小，确定性系数增大，说明该方法有效可行；同时也注意到，修正前洪峰流量真值大于计算值，相对误差为5.4%，权重系数取0时，即应用DSRC方法，修正后计算洪峰超出了洪峰真值，相对误差变为-7.9%，显然出现了矫枉过正现象，洪量修正也出现了同样的结果，这是DSRC方法修正不稳定的表现，当权重系数逐渐增大时，方法的修正效果趋于稳定；图2显示平均产流修正比重随权重系数的增大而减小，说明权重系数越大修正结果越稳定，另外，平均产流修正比重减小幅度开始很大并随权重系数的增大趋于平缓，说明一定范围内较小的权重系数就能对修正结果的稳定起到很大的作用；图3反映了权重系数与修正效果之间的关系，当权重系数由0逐渐增大时，洪峰误差与洪量误差显著减小，当权重系数达到某一个值时，修正效果达到最好，洪峰误差与洪量误差趋于0，这时如果再增大权重系数，那么修正效果将受到影响，影响程度随权重系数的增大而增大，但无论权重系数多大，RESM方法始终具有一定的修正效果，洪峰和洪量误差总是小于修正前的结果。

3.2实际案例分析实际案例采用达开水库洪水过程，达开水库位于广西贵港市、桂平市和武宣县交界的马来河下游，马来河又称龙山河、六红河，发源于贵港市大平天山，是西江水系黔江的一级支流，流向东北方向，最终在桂平市石龙镇东岗村汇入黔江，流经贵港市中里乡、奇石村以及桂平市石龙镇新龙村，主河道长约70.2 km，流域面积为474.92 km2，河道平均比降为0.209%。达开水库坝址以上河道长48 km，集水面积为426.8 km2。达开水库流域属大瑶山余脉的莲花山系，地形山峦重叠，库区呈狭长型，地势中间低，南北高，流域内多为高低不等的丘陵地区，边界大部分为高山。达开水库流域地处低纬度湿润地区，雨量充沛，气候温和，属南亚热带季风气候，流域多年平均气温21.5℃，多年平均降雨量为1 500 mm，多年平均蒸发量1 426.3 mm，多年平均相对湿度为77.3%。降雨年际及年内分配不均，年内降雨集中在五月到八月份，夏秋两季占全年降雨量的一半以上。达开水库水量较丰沛，多年平均径流量为3.52亿m3，流量年内分配不均匀。

应用RESM方法对达开水库19场历史洪水做了模拟计算与误差修正，结果统计见表2、表3。表2显示，对于多数洪水，RESM方法预报精度均能达到要求，修正效果较好，且平均产流修正比重多保持在0.35以内，修正结果稳定。表3数据显示，采用RESM方法，平均洪峰相对误差由17.3%下降到8.1%，平均洪量相对误差由9.5%下降到5.1%，修正效果显著，另外，平均确定性系数由0.704提高到0.813，平均峰现时差由1.2 h降到0.7 h，也说明该方法的有效性，能够提高洪水预报精度；说明RESM方法在满足稳定性的同时有效提高了预报精度，改善了修正效果。

表1 理想案例权重系数与修正效果关系表

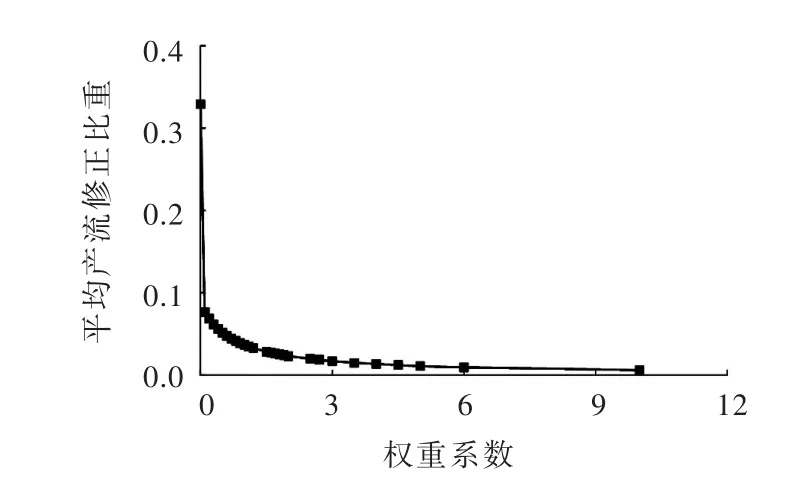
图2 RESM方法权重系数与修正稳定性关系

图3 RESM方法权重系数与修正效果关系

同一场洪水，产流修正时段数和修正所用真值流量数一定的情况下，探讨权重系数、观察洪水修正效果、修正稳定性的变化。应用效果如表4、图4、图5。

表2 RESM方法达开水库流域应用结果

表3 RESM方法达开水库流域应用平均效果

表4、图4和图5显示，实际案例的分析结果与理想案例极为相似，对于实际洪水权重系数无论取多少，RESM方法均具有一定的修正效果；同时也注意到，修正前实测洪峰小于计算值，相对误差为-32.5%，权重系数取0时，即应用DSRC方法，修正后计算洪峰超出了洪峰真值，相对误差变为19%，显然出现了矫枉过正现象，洪量修正也出现了同样的结果，这是DSRC方法修正不稳定的表现，当权重系数逐渐增大时，RESM方法的修正效果趋于稳定；图4反映了权重系数与相对误差之间的关系，当权重系数由0逐渐增大时，洪峰误差与洪量误差显著减小，当权重系数达到某一个值时，修正效果达到最好，洪峰误差与洪量误差趋于0，这时如果再增大权重系数，那么修正效果将受到影响，影响程度随权重系数的增大而增大，且趋势趋于平缓，但无论权重系数多大，RESM方法始终具有一定的修正效果，洪峰和洪量误差总是小于修正前的结果；图5显示了权重系数与确定性系数之间的关系，起始确定性系数随权重系数的增大而增加，随后便随之减小，权重系数取某一值时，确定性系数达到最大。将图4与图3比较，可以得出，实际流域中的最优权重系数往往较大，实例中约为20.3，这主要是由于实际流域水文规律复杂，有效信息提取比较困难。

4 结论

通过理想案例和实际案例对RESM方法进行分析，得到如下几点结论：

（1）达开水库流域的应用效果显示，RESM方法具有较好的误差修正效果，提高了洪水预报精度，平均洪峰相对误差由17.3%下降至8.1%，平均洪量相对误差由9.5%下降至5.1%；

（2）RESM方法受权重系数的影响比较严重，存在一个最优的权重系数使得RESM方法的修正效果达到最好，本实例中约为20.3，并且权重系数的敏感性随其增大而减小，但无论权重系数是否达到最优，RESM方法都具有一定的修正效果；

（3）在实际流域应用RESM方法时，权重系数往往较大，文中实例约为20.3，是由于水文规律复杂，有效信息提取较困难。

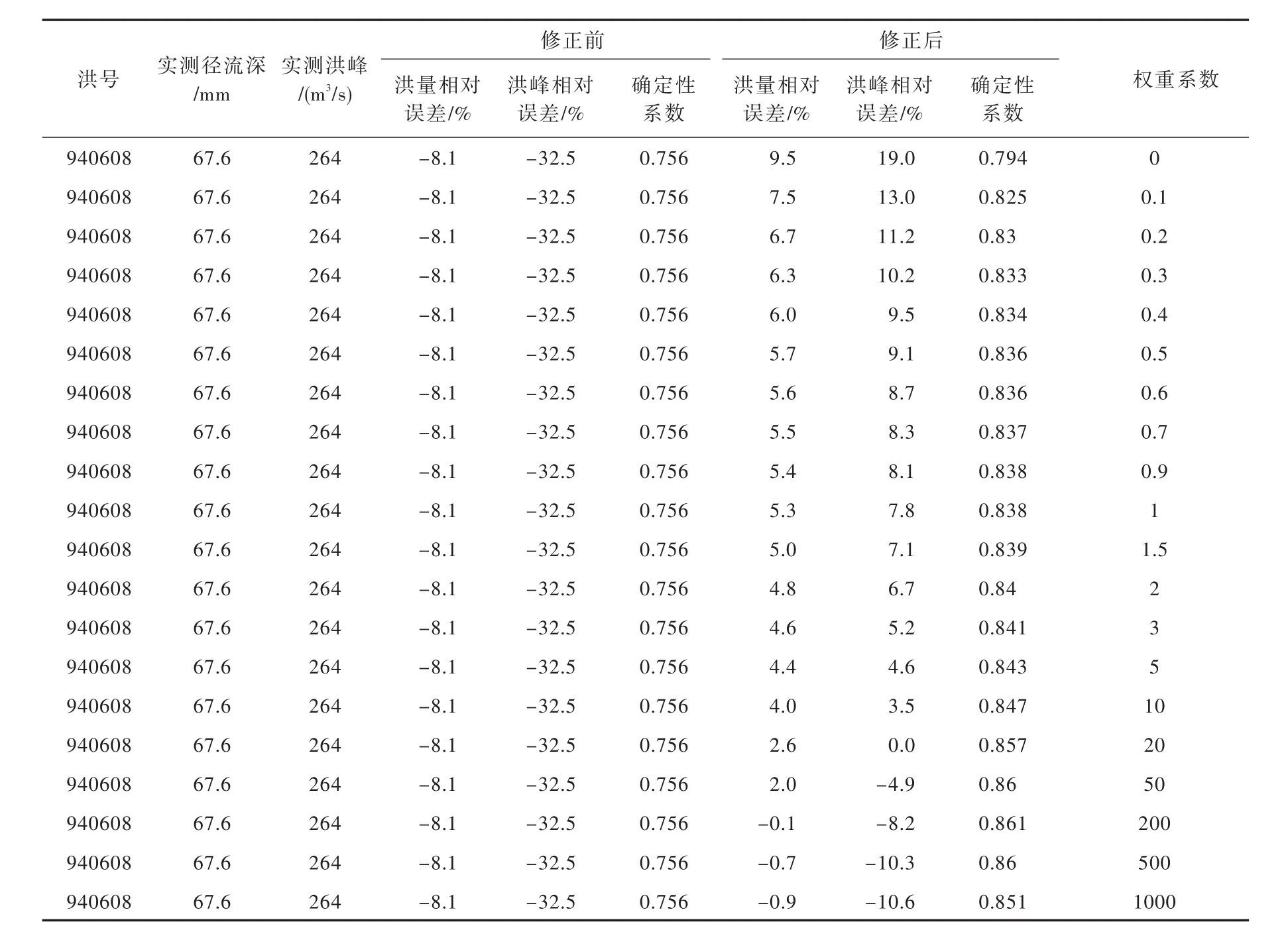
表4 实际案例权重系数与修正效果关系表

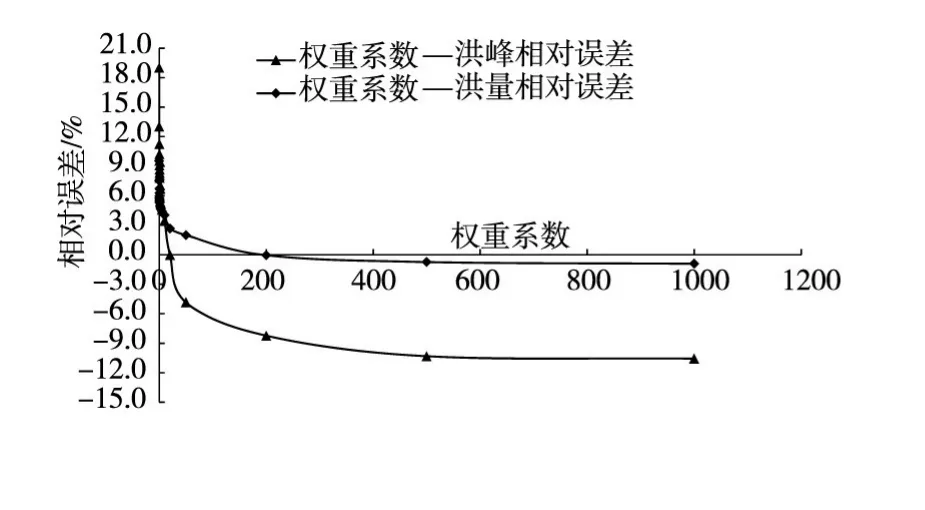
图4 RESM方法权重系数与相对误差关系图

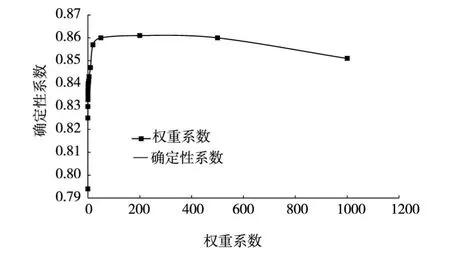
图5 RESM方法权重系数与确定性系数关系

［1］BRATH A，MONTANARI A，TOTH E.networks and non-parametric methods for improving real-time flood through conceptual hydrological models［J］.Hydrology and Earth System Science，2002，6（4）：627-640.

［2］王厥谋，乐嘉祥.1991年中国的洪水和洪水预报［C］//第二次中美水文情报预报研讨会论文集.1995.

［3］王猛.石佛寺水库洪水预报及其实时修正方法研究［D］.大连：大连理工大学，2012.

［4］李致家.现代水文模拟与预报技术［M］.南京：河海大学出版社，2010.

［5］周轶，菅浩然，李致家，等 .基于递推最小二乘改进算法的洪水预报模型研究［J］.河海大学学报，2007，35（1）：77-80.

［6］WU X L，XIANG X H，WANG C H，et al.Coupled Hydraulic and Kalman Filter Model for Real-Time Correc⁃tion of Flood Forecast in the Three Gorges Interzone of Yangtze River，China［J］.Journal of Hydrologic Engineer⁃ing，2013，18：1416-1425.

［7］王船海，白耀玲.基于卡尔曼滤波技术的河道汇流实时校正［J］.河海大学学报，2007，35（2）：181-187.

［8］郭磊，赵英林.基于误差自回归的洪水实时预报校正算法的研究［J］.水电能源科学，2002，20（3）：25-27.

［9］包为民，司伟，沈国华，等.基于单位线反演的产流误差修正［J］.水科学进展，2012，23（3）：315-322.

［10］BAO W M，SI W，QU S M.Flow Updating in Real-Time Flood Forecasting Based on Runoff Correction by a Dy⁃namic System Response Curve［J］.Journal of Hydrologic Engineering，2014，19：747-756.

［11］司伟，包为民，瞿思敏.洪水预报产流误差的动态系统响应曲线修正方法［J］.水科学进展，2013，24（4）：497-503.

［12］刘可新，包为民，李佳佳，等.基于系统响应理论的分水源误差修正［J］.水电能源科学，2014，11：44-47.

［13］张小琴，刘可新，包为民，等 .产流误差比例系数的系统响应修正方法［J］.水科学进展，2014，25（6）：789-796.

［14］杨姗姗，包为民，杨小强，等.微分响应在降雨修正中的应用［J］.中国农村水利水电，2015（11）：75-79.

［15］刘可新，包为民，赖善证，等.产流误差动态系统响应曲线修正方法在乌溪沟流域的应用［J］.中国农村水利水电，2014（12）：24-26.

［16］SI W，BAO W M，WANG H Y，et al.The research of rainfall error correction based on system reponse curve［C］//GBMCE2013.335-339.

［17］SI W，BAO W M，GUPTA H V.Updating real-time flood forecasts via the dynamic system response curve meth⁃od［J］.Water Resources Research.2015，51（7）：5128-5144.doi：10.1002/2015WR017234.

［18］阙家骏，包为民.产流误差的动态系统响应曲线修正方法应用［J］.三峡大学学报（自然科学版），2014，36（6）：6-9.

［19］BAO W M，ZHAO L P.Application of Linearized Calibration Method for Vertically Mixed Runoff Model Parame⁃ters［J］.Journal of Hydrologic Engineering，2014，19（8）：481-486.

［20］刘可新，张小琴，包为民，等 .产流误差平稳矩阵的系统响应修正方法［J］.水利学报，2015，46（8）：960-966.