土石坝边坡小概率失效计算方法

杜建刚，徐佳成，罗显枫，李 昕

（1.中国国际工程咨询公司 能源业务部，北京 100048；2.大连理工大学 建设工程学部，辽宁 大连 116023 3.湖北理工大学 土木建筑工程学院，湖北 黄石 435003）

1 研究背景

在工程实际中经常需要对一些小概率失效的土石坝进行安全性评价分类，例如水库土石坝的坝坡稳定性安全评价（规范要求其失效概率数量级小于10-5）。面对此类情况时，如果采用直接蒙特卡罗随机有限元模拟方法则必须抽取105数量级以上的样本才能估算其失效概率，导致计算时间冗长［1］。而子集模拟法是一种针对小概率失效问题的分层抽样算法，在每一层中引入合理的中间失效事件，将小概率问题表示成一系列较大的条件概率的乘积［2-4］。而计算每一层的条件概率所需要抽取的样本数量非常少，因此它计算失效概率所要的样本总数量要远小于直接蒙特卡罗模拟方法需要的样本数量。另一方面，很多商业岩土仿真软件常采用基于土的弹塑性本构的强度折减法计算边坡安全系数，该方法本质上是一种弹塑性增量有限元方法，而且在边坡安全系数计算中还经常使用基于二分搜索法的强度折减法来反复搜索边坡安全系数的上下界限以至消耗机时过长［5］，而链表筛分算法无需反复迭代搜索边坡安全系数的上下界限，从而能快速计算多个样本点的安全系数。因此可以在子集模拟法的第一层初始样本点的响应值计算中采用链表筛分算法来节省计算机时。而在子集模拟法的其余分层模拟中，可通过经过初始样本点训练后的Kriging代理模型来预测条件样本点的响应值，从而能进一步节省机时。

本文根据以上分析，提出了基于链表筛分法和kringing代理模型的混合子集模拟法，并通过算例说明本方法的有效性。

2 基于链表筛分法和Kriging代理模型的混合子集模拟法

2.1链表筛分法链表筛分法能自动计算出按边坡安全系数FS大小升序排列的样本集，其算法原理框图见图 1 所示［5］。从图中可看到土性参数黏聚力c=(c1，c2，...，cN)和内摩擦角φ =(φ1，φ2，...，φN)是输入宗量，是对边坡土性参数c和φ分别进行直接蒙特卡罗模拟时产生的样本。当边坡土性参数的赋值为样本对(cj，φj)时可计算得到相应的边坡安全系数FS(cj，φj)，(j=1，2，…，N)。图1所示的边坡安全系数初始顺序搜索区间为FOS(l)=(M/LMAX)*l，(l=1，2，...)，LMAX（l代表加载的增量步序列号，LMAX代表最大增量步数）。然后利用弹塑性有限元增量加载的计算特性，在第l次增量步计算中筛选出达到最大迭代次数i=IMAX的样本点（i代表迭代序列号），该样本点对应的边坡安全系数就是FOS(l)。因此，链表筛分算法实际具有按边坡安全系数从小到大增量顺序搜索这一特性，所以输入土性参数c和φ，可以自动计算出按边坡安全系数从小到大顺序排列的安全系数FS。而如图2所示商业软件中采用的二分搜索法要进行直接蒙特卡罗模拟时，只能按样本产生的顺序(cj，φj)来计算对应的FS(cj，φj)(j=1，2，…，N)。另外，二分法常常需要把搜索上下界限设置为固定常数（图2中t1=0，t2=5），这样会导致当边坡的实际安全系数远小于二分法初始上界时，二分法搜索目标安全系数耗时过长。

2.2Kriging模型Kriging模型假定系统样本x的响应值为随机过程函数y(x)，由回归模型和随机误差组成［6］，即

式中；βj为回归系数；fj(x)为基函数；z(x)为二阶平稳的随机过程。

另外，Kriging模型采用已知样本x1，x2，…，xm的响应值 y1，y2，...，ym的线性组合来预测待测样本点x的响应值，即

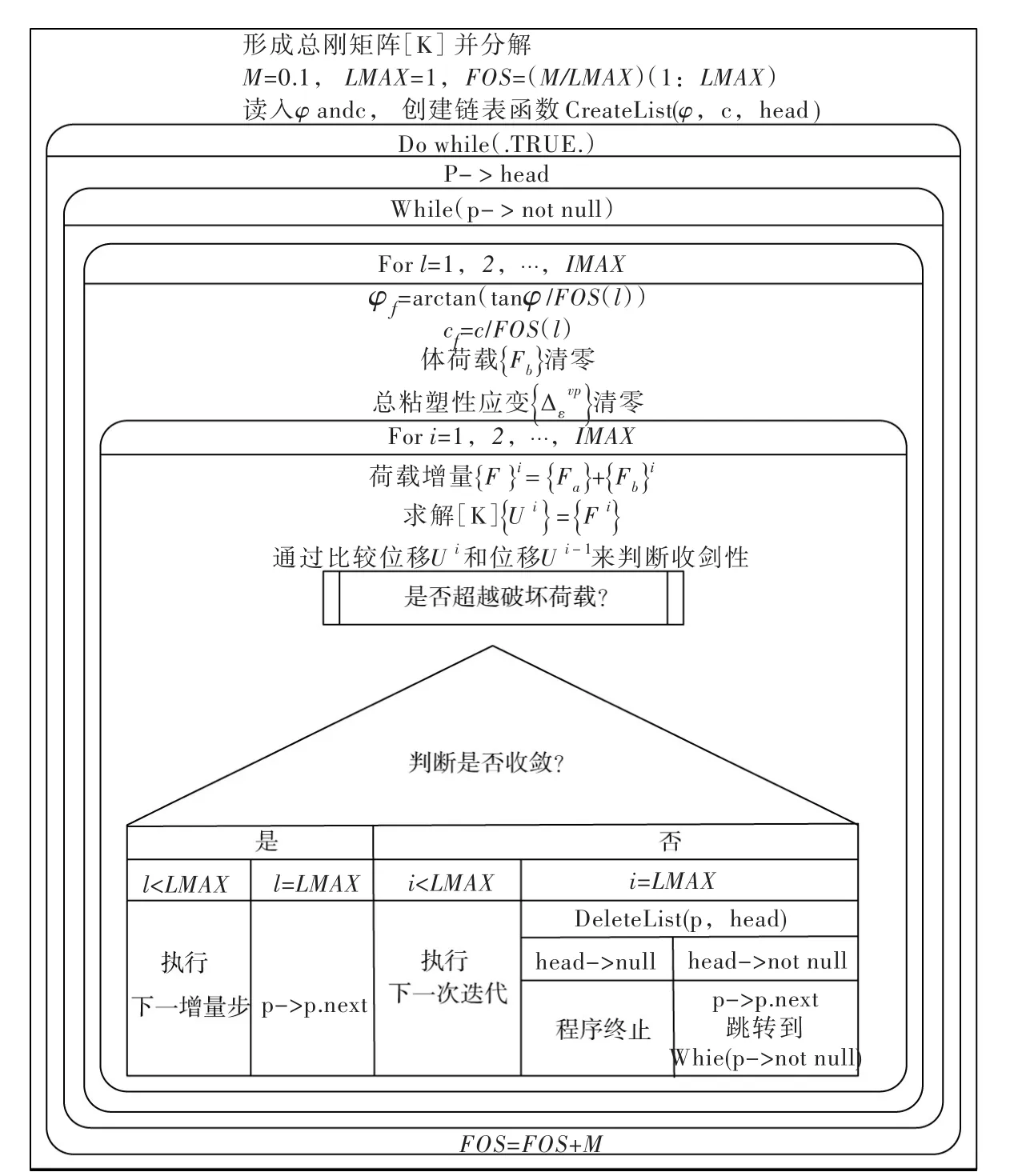
图1 链表筛分法程序结构框图

由于Kriging对y^(x)采用的是无偏估计，则需使其预测值的均方误差E[(y^(x)-y(x))2]达到最小值。这样便可求出系数c1，c2，...，cm及y^(x)。详细推导步骤可参见相关文献，在此不做赘述。

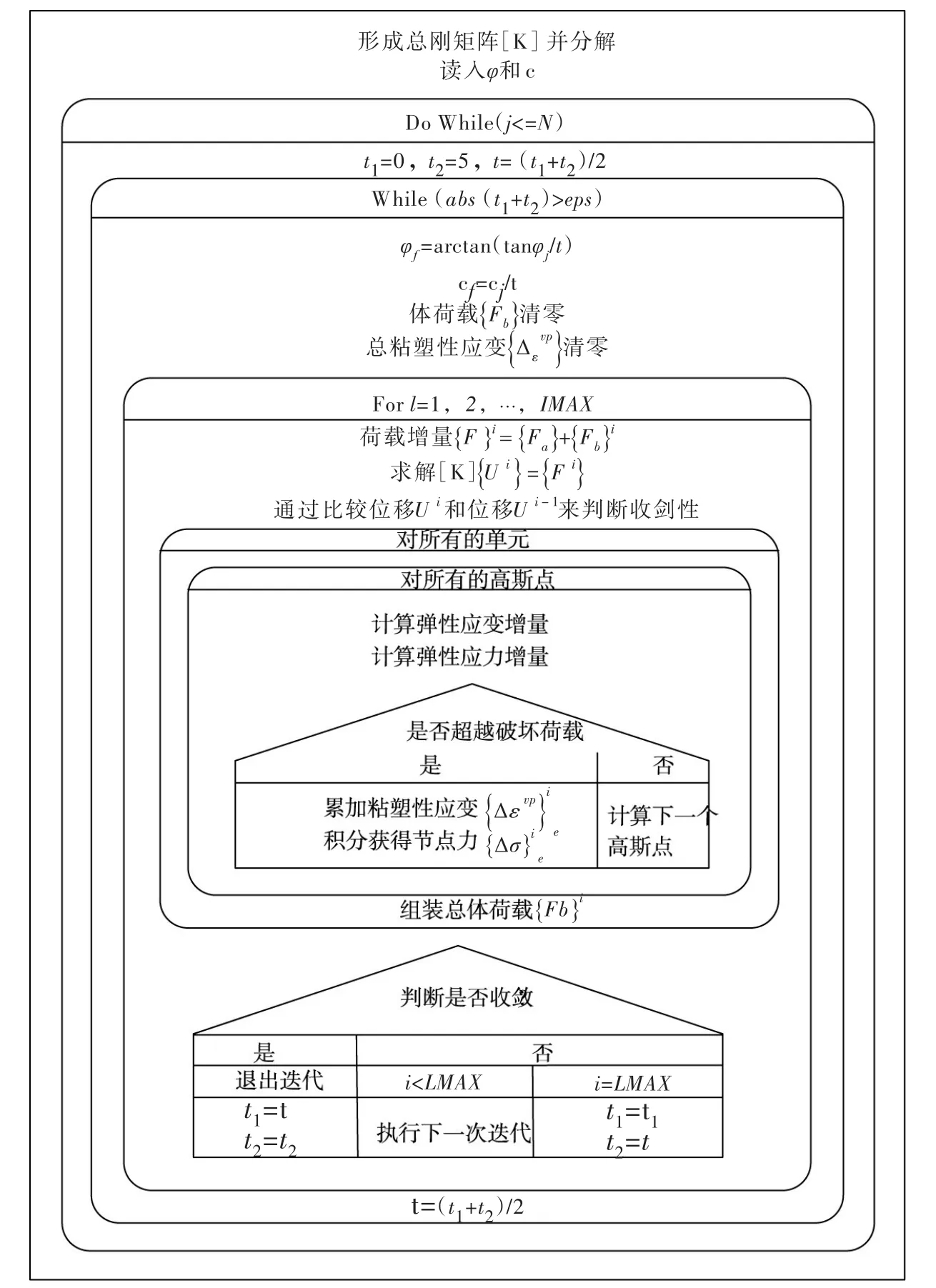
图2 二分法程序结构框图

2.3子集模拟法结构的失效概率可以表示为

式中： fX(x)=fX(x1，x2，…，xn)是随机变量X=(X1，X2，…，Xn)T的联合概率密度函数；y(x)是极限状态函数；y(x)＜0代表结构失效。

对于边坡稳定失效时，极限状态函数y(x)可以表示为

式中：x一般是边坡土层的土性参数；FS(x)是把x输入边坡稳定分析程序后计算得到的边坡安全系数。

在子集模拟中，一个很小的结构失效概率pf被认为是一系列较大的条件失效概率的乘积［7］

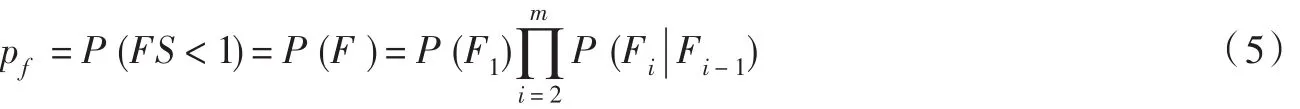
式中：Fi={ }FS＜fsi，(i=1，2，…，m)， 表示一系列中间失效事件；P(Fi)=P(FS＜fsi)表示中间失效事件Fi发生的概率；fsi表示中间失效事件Fi发生的阈值；这些阈值的大小顺序依次为fs1＞fs2＞…fsm=1；这些中间失效事件满足包含关系F1⊃F2⊃…⊃Fm=F；P(Fi|Fi-1)=P(FS＜fsi|FS＜fsi-1)表示已知中间失效事件Fi-1发生时，中间失效事件Fi发生的概率。由于P(Fi|Fi-1)的概率大于P(F)，所以需要的样本数量也要少，另外在子集模拟中，用马尔可夫蒙特卡罗法（Markov Chain Monte Carlo，MCMC）［8］计算P(Fi|Fi-1)所需要的样本数量也远小于直接蒙特卡罗方法。

2.4基于混合子集模拟法的边坡失效概率计算如研究背景中所提到的，可以利用链表筛分算法自动计算出按边坡安全系数大小升序排列的样本集。这一样本集合可以作为子集模拟法的第一层有序样本集，并用该样本集来训练Kriging模型。然后在子集模拟法的中间事件的样本模拟中采用Kriging模型预测各个条件样本点的边坡安全系数。具体做法如下

（1）步骤1。用直接蒙特卡罗模拟方法产生N个独立同分布的样本

（2）步骤2。利用链表筛分法计算按升序排列的边坡安全系数即样本的响应值，(j=1，2，…，N)。取其升序排列后的第Np0+1个值作为第一层中间失效事件发生的阈值fs1。

（6）步骤 6。重复步骤 4和 步骤 5直到进入第m层失效域此时条件概率的估计值为是落在失效域Fm的样本数量）。

3 土石坝边坡可靠度计算实例

3.1计算实例本节用一个关于土石坝边坡稳定失效概率计算的例子来说明所提方法的有效性。这一算例来自于文献［9］。边坡的几何形状及土层划分如图3所示。边坡各土层的土性参数如表1所示。表中属于随机变量的土质指标均认为服从对数正态分布。有限元计算采用八节点四边形单元的平面应变模型。为了和文献［9］对比，这里的有限元模型也划分为1 407个单元。约束条件是边坡的底边界固定约束，左右边界水平约束。土体本构采用理想弹塑性模型和摩尔-库伦破坏准则。

3.2本文方法计算结果图4给出第一层全部样本的频率直方图（本例中N=300），从频率直方图中能看出边坡安全系数最小值约为1.2，边坡安全系数最大值约为3.9。这说明直接蒙特卡罗模拟法的抽样中心远离失效域FS≤1。图5（a）显示出由子集模拟法第二层的第一个样本产生的条件样本点的响应值因为在本例中假定p0=0.1，所以马尔可夫链的长度L=9。从图5（a）中可以看出由于满足Metropolis-Hasting算法的接受准则，初始状态需要进行更新，因此移动到。而与相等是因为不满足Metropolis-Hasting算法的接受准则，所以即时状态保持不变。图5（b）显示出由子集模拟法第四层的第一个样本产生的条件样本点的响应值从图5

（b）中可以看出这些样本点全部落在失效域FS≤1。这也说明子集模拟法通过分层模拟条件样本点，容易抽取到落入FS≤1失效域内的样本点。

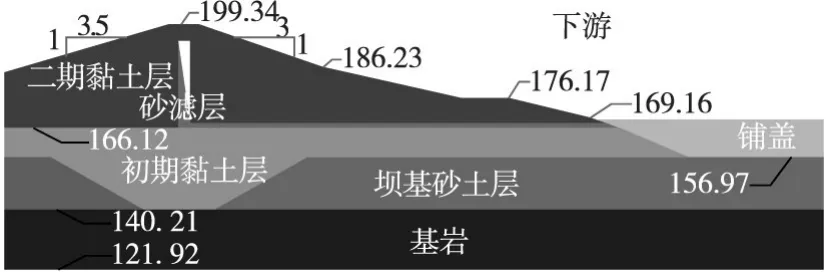
图3 边坡的几何形状及土层分区 （单位：m）

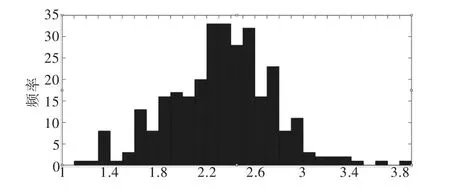
图4 首层全部样本响应值FS(x(1))的频率直方图

表1 各土层的土性参数

图5 不同条件样本点响应值

为了说明Kriging代理模型在分层模拟中的预测效果，图6（a）给出了Kriging代理模型对条件样本点的响应值的预测值与有限元法算出的边坡安全系数（即目标值）的对比。图中9个圆圈的中心位置非常靠近与坐标轴成45°夹角的直线（其中有3个圆圈的中心是重合的），说明Kriging代理模型对分层模拟的第二层条件样本点的响应值预测效果显著。图6（b）给出了Kriging代理模型对条件样本点的响应值的预测值与有限元法算出的边坡安全系数（即目标值）的对比。图中9个圆圈的中心位置非常靠近与坐标轴成45°夹角的直线（其中有4个圆圈的中心是重合的），说明Kriging代理模型对分层模拟的第四层条件样本点的响应值预测效果同样显著。

图6 不同条件样本点的响应值预测效果

图7 顺序搜索FS和二分搜索FS

图8 FS顺序搜索和二分搜索FS

3.3 本文方法与其它方法比较图7（a）显示了链表筛分法计算FS()时在弹塑性有限元分析的每一增量步中所需要的迭代数。从图中可以看出当强度折减系数接近目标边坡安全系数时，则对应该强度折减系数的增量步中所需要的迭代数也迅速增加。如图所示，顺序搜索的总迭代数为2+2+2+2+2+2+2+4+9+9+25+35+67+135+216+500=1014。图7（b）显示了二分法计算FS)时对每一次的强度折减系数计算时所花的迭代数。从图中可以看到二分搜索的总迭代数为500+500+2+16+235+500+400+500=2653。图8（a）显示了链表筛分法计算FS()时在弹塑性有限元分析的每一增量步中所需要的迭代数。从图中能看出当强度折减系数接近目标边坡安全系数时，则对应该强度折减系数的增量步中所需要的迭代数也迅速增加。如图所示，总迭代数为2+2+2+2+2+9+15+18+26+43+117+295+500=1033。图8（b）显示了二分法计算FS()时对每一次的强度折减系数计算时所花的迭代数。从图中可以看到总迭代数为500+500+17+500+500+35+300+500=2852。

图9 顺序搜索min()和顺序搜索max()

另外，如果采用直接蒙特卡罗方法计算边坡失效概率，则只需判断FS(x)＜1是否为真，而不用去计算FS(x)，所以需要的总迭代数只相当于验算强度折减系数为1时的迭代数。如图9（a）所示判断第一层最小边坡安全系数样本所需要的迭代数是9，而利用顺序搜索法计算其安全系数所经历的迭代总数为2+2+2+2+2+2+2+2+9+9+14+17+21+28+43+89+154+252+500=1152。如图9（b）所示判断第一层最大边坡安全系数样本所需要的迭代数是2，而利用顺序搜索法计算其安全系数所经历的迭代总数为2*30+6+13+18+21+28+37+41+56+60+68+145+226+304+367+433+500=2383。因此，判断FS(x)＜1是否为真所需要的迭代数远远少于计算FS(x)所需要的迭代总数。但是考虑到本算例的失效概率在10-4这个数量级上，所以必须进行104数量级以上的直接蒙特卡罗模拟抽样才能得到满意结果。而子集模拟法在本算例的初始样本抽取即第一层抽样中只需要计算300个样本点的FS值，在其余各分层抽样需要各自计算270个样本点的FS值。所以不采用Krig⁃ing代理模型的子集模拟法总共需要计算1110个样本点的FS值。而采用Kriging代理模型后，只需要计算348个样本点的FS值（T1其中48个样本点为第二到四层中为提高Kriging预测精度所增设的样本点）。所以图10给出了方法1（T1直接蒙特卡罗法），方法2（T2子集模拟法+链表筛分法），方法3（T3子集模拟法+二分法+Krig⁃ing）和方法4（T4子集模拟法+链表筛分法+Kriging）的时间对比。从图中显示，方法4即本文所提方法所用时间最少，约为方法1的一半。如果遇到失效概率更小的算例时，则本文方法的优点会更加明显。

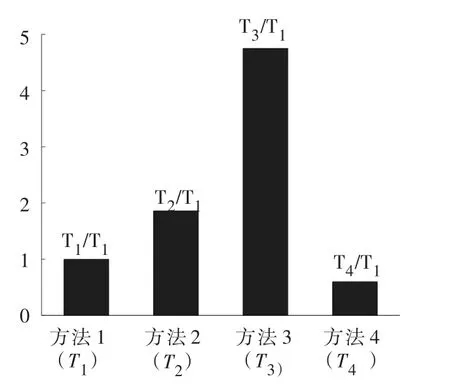
图10 各方法的时间对比图

4 结论

本文提出了一种土石坝边坡小概率失效计算方法。该方法利用链表筛分算法自动计算出按边坡安全系数大小升序排列的样本集。这一样本集合可以作为子集模拟法的第一层有序样本集。然后第一层样本集可以用来训练Kriging代理模型。接着在子集模拟法的中间事件的样本模拟中采用Kriging代理模型来预测条件样本的边坡安全系数，这样可以避免对条件样本点的弹塑性有限元计算。另外，该方法所采用的子集模拟部分引入了合理的中间失效事件将失效概率表达为一系列较大的条件失效概率乘积，因此只需要在子集模拟的每一层计算中抽取少量样本点，就能使抽样中心快速向失效域移动。对于本文所提供的10-4数量级的边坡稳定的失效概率求解范例中，只需要进行子集模拟的四层抽样计算，就能和直接蒙特卡罗模拟方法的结果非常接近。这足以说明本文所提方法的有效性。此外，通过本文方法与直接蒙特卡罗方法的计算时间分析比较中，可以看出本文方法更适合计算边坡小概率失效问题。

［1］LI D，XIAO T，Cao Z，et al.Enhancement of random finite element method in reliability analysis and risk assess ment of soil slopes using Subset Simulation［J］.Landslides，2016，13（2）：293-303.

［2］宋述芳，吕震宙.基于马尔可夫蒙特卡罗子集模拟的可靠性灵敏度分析方法［J］.机械工程学报，2009，45（4）：33-38.

［3］宋述芳，吕震宙.基于子集模拟和重要抽样的可靠性灵敏度分析方法［J］.力学学报，2008，40（5）：654-662.

［4］宋述芳，吕震宙.高维小失效概率可靠性分析的序列重要抽样法［J］.西北工业大学学报，2006，24（6）：782-784.

［5］LUO X，CHENG T，LI X，et al.Slope safety factor search strategy for multiple sample points for reliability analy⁃sis［J］.Engineering Geology，2012，129：27-37.

［6］LUO X，LI X，ZHOU J，et al.A Kriging-based hybrid optimization algorithm for slope reliability analysis［J］.Structural Safety，2012，34（1）：401-406.

［7］AU S，BECK J L.Estimation of small failure probabilities in high dimensions by subset simulation［J］.Probabi⁃listic Engineering Mechanics，2001，16（4）：263-277.

［8］LI H，CAO Z.Matlab codes of Subset Simulation for reliability analysis and structural optimization［J］.Structur⁃al and Multidisciplinary Optimization，2016，54（2）：391-410.

［9］CHO S E.Probabilistic stability analyses of slopes using the ANN-based response surface［J］.Computers and Geotechnics，2009，36（5）：787-797.