基于角度约束空间殖民算法的树点云几何结构重建方法
2018-03-13胡少军张志毅何东健
师 翊 何 鹏 胡少军 张志毅 耿 楠 何东健
(1.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100; 2.西北农林科技大学信息工程学院, 陕西杨凌 712100)
0 引言
树是十分常见的自然景观之一,在农林生产中,许多树种也是重要的经济作物,构建树的三维模型和模拟树的生长过程对研究植物生长规律有着重要意义[1]。在自然环境中,树的几何结构复杂,如何重构树的三维模型一直是现代农业信息化领域与计算机图形学研究中的一个难题。近年来,信息技术与农业的联系愈发紧密,“数字植物”概念的提出,为树木的研究提供了新的思路与手段[2]。
树的可视化三维模型始于HONDA[3]提出的递归树模型。目前对于树的建模可以归纳为以下几类:基于规则的建模、基于草图的建模、基于图像的建模和基于点云数据的建模。基于规则的建模主要有PRUSINKIEWICZ等[4]提出的改进L-system以及LINERMANN等[5]提出的Xfrog系统。基于规则的方法依据树木的分形特征提出,能够在短时间内建立真实感较高的树模型,但是重建出的模型植物学特征细节展现不够。基于草图的建模主要由OKABE等[6]提出,用户需要勾勒出树枝或者树冠的轮廓草图即可推算生成三维模型,WITHER等[7]对此方法进行改进,用户只需绘制树的轮廓即可重建三维模型。但是基于草图方法生成的树模型只能反映树的二维结构,树冠层内部的三维形态依据模型库生成,且重建的精度不高。基于图像的建模方法主要是根据树的真实照片、视频等恢复树的三维信息。QUAN等[8]以及TAN等[9]实现了基于多幅图像的树模型三维重建,该方法使用树的真实图像较好地重建了树的三维几何模型,但是需要从不同角度采集多幅图像,图像的复杂背景对重建精度影响很大,重建的精度较低。基于点云数据的重建方法是使用三维激光扫描设备采集植物的三维点云数据,在此基础上进行三维重建。XU等[10]提出了基于树的单面扫描点云重建三维模型的方法;LIVNY等[11]提出基于Lobe的树重建方法,将树的冠层分为多个Lobe,并根据模型库合成Lobe内部树枝,生成了完整的树三维模型;XIE等[12]基于实测点云数据构建树的范例库,提高了重建模型的真实感;RUNIONS等[13]将空间殖民算法从二维空间扩展到三维空间,进行了树的重构;ZHANG等[14]在提取骨架时,直接将冠层的特征点作为骨架点,使用粒子流法将骨架连接,取得了较好的重建效果;唐丽玉等[15]基于冠层特征点与主干骨架点的拓扑关系重构出了精度较高的树三维模型。
与本文关联较为密切的是文献[13-15]提出的重构方法,原空间殖民算法虽然可以重构出高真实感的树模型,但是冠层点云基于规则生成,与真实树有一定差距,并且会有部分不合理的枝条出现;文献[14]中提取骨架的方法对枝干细节模拟不够;文献[15]使用分治思想,将枝干与树叶分离后再生成完整骨架,过程较为繁琐,并且在枝条建模时,人为设定细枝的半径是父节点半径的0.8倍,影响了模型精度,此外,使用的扫描设备较为昂贵,不利于普及。
本文以实测点云为依据,尝试一种高精度、低成本的方法重建树的三维模型。使用Kinect 2.0多角度采集树的原始点云数据,采用人工标记法与迭代最近点(Iterative closest point,ICP)算法结合的配准方法获得完整点云数据,以真实树点云作为输入对象,采用改进的空间殖民算法提取树点云对应的三维骨架,基于骨架坐标由广义圆柱体表示树干的几何模型,再通过叶序规则添加树叶,最终得到树的三维模型。
1 数据获取
1.1 数据采集
数据获取采用微软公司生产的Kinect 2.0作为采集设备。Kinect 2.0是Kinect 1.0的更新版本[16],采用飞行时间原理(Time of flight)获取点云数据,精度更高,可达0.02 mm,有效深度范围0.5~4.5 m,有效帧率30 f/s,可获取颜色信息与深度信息 (RGB-D)数据,满足重构需求[17]。数据采集于2016年8月,在西北农林科技大学校园内进行,采集现场与获取的RGB图像如图1所示。

图1 数据采集Fig.1 Data acquisition
1.2 数据去噪与配准
使用Kinect 2.0获取的树点云数据由于设备、环境、人为操作等因素不可避免的带有噪声,噪声会对后续的配准工作造成较大影响,因此,首先对采集到的原始数据进行去噪处理。
噪声主要分为大尺度噪声与小尺度噪声[18],所获数据的大尺度噪声主要指扫描到的大片地面点云数据,小尺度噪声指围绕在树周围的离群散点。从图2a可以看出,由于地面平坦,大尺度噪声点云密集,与树主干垂直在X-Z平面分布,小尺度噪声密度稀疏呈离散分布。针对噪声数据的不同特点,采取不同的去噪方法,大尺度噪声使用直通滤波去除,小尺度噪声使用Statistical outlier removal滤波器[19]去除。直通滤波的具体做法为:建立直通滤波器,观察地面点云坐标可知,Y轴坐标范围在-3~-1.5之间,故设定过滤Y轴方向上阈值区间为[-3,-1.5]内的数据,过滤结果如图2b所示。Statistical outlier removal滤波器基于K近邻原理实现,K越大且λ越小时,去噪效果越明显,λ为缩放因子,经验取值为[0,1]。针对参数K与λ的取值问题,根据不同点云数据,依据经验取值进行多次试验。分别选取K为30、50、100,λ为0.2、0.5、1,分9组进行去噪试验。图3中,λ=0.2时,部分枝叶点云被当做噪声去除,K=30,λ=0.5时,有些噪声没有被去除,当K=50,λ=0.5时,去噪效果最好,部分对比效果如图3所示。
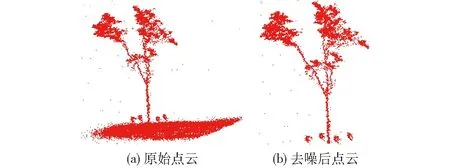
图2 地面噪声去除结果Fig.2 Result of removing ground noise

图3 离群散点去除结果对比(红色为噪声点)Fig.3 Comparisons of removing noise (noise was shown in red color)
为保证数据的完整性,采取双面采集策略,然后对两片点云进行配准处理[20]。由于两次采集的数据不在同一个坐标系内,配准的过程是通过平移、旋转和缩放进行坐标转换,将两片点云转换到同一坐标系下,原理为
(1)

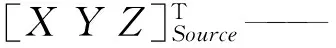
[ΔXΔYΔZ]T——平移矩阵
R——旋转矩阵
根据姚吉利[21]的研究,两坐标系下有3个以上的公共点时可以进行三维坐标转换,并给出了3点法与4点法的计算方法。为了使配准过程更加便捷,使用人工标记法进行粗配[22],具体做法是:
(1)采集数据时,在树的附近放置4个塑料球,如图1a所示,球直径为11 cm。
(2)采用Meshlab软件对4个球的点云数据进行分割,使用最小二乘法拟合球心,将球心坐标作为4个公共点。
(3)将4点球心坐标代入文献[21]中的计算公式,计算得出缩放因子λ、平移矩阵[ΔXΔYΔZ]T、旋转矩阵R。
(4)根据旋转矩阵、平移矩阵与缩放因子进行配准,粗配结果如图4a所示。
为进一步提高配准精度,精配阶段,使用ICP算法。ICP算法虽然配准精度高,但是存在耗时较长,初始位姿不好易陷入局部最优等缺点,在本文中,经过人工标记法粗配准后,两片点云已经大致重合,将粗配结果作为ICP算法的初值,不会使算法陷入局部最优,最终的配准结果如图4b所示。
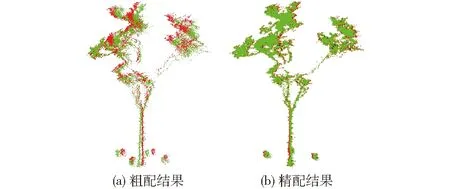
图4 配准过程Fig.4 Process of registration
2 树的三维重构
2.1 树骨架提取
采集到的原始点云数据经过去噪、配准等预处理后,可以得到质量较高的完整树点云数据。在进行树的三维重构时,树干部分主要基于树骨架绘制广义圆柱体生成,骨架的走向直接影响了三维重构的精度。由于树的冠层结构复杂,有较为严重的遮挡与交叉现象,对骨架提取造成了较大干扰,针对这一特征,空间殖民算法被RUNIONS等[23]提出并扩展至三维空间,得到了广泛应用。
使用Kinect 2.0获取点云数据时,冠层以下的部分由于没有遮挡,树干结构十分清晰,此部分提取骨架信息较为容易,被冠层遮挡的枝干部分是骨架提取的难点,也是空间殖民算法解决的核心问题。该算法基于树木生长空间竞争的原理,可以在遮挡情况下较好地提取树骨架数据。在骨架提取过程中,依据“就近影响”原则,生长点邻域内的空间空白点影响骨架走向,骨架依次生成,直至没有点影响骨架时算法结束。但是,使用空间殖民算法时,会有部分生长方向不合理的枝条出现。针对此问题,本文引入生长角度约束对空间殖民算法加以改进,根据树木向上趋光性的生长特征,枝干与次级枝干保持约为60°的夹角,因此将生长角度约束设置为60°。本文改进后的空间殖民算法实现过程为:
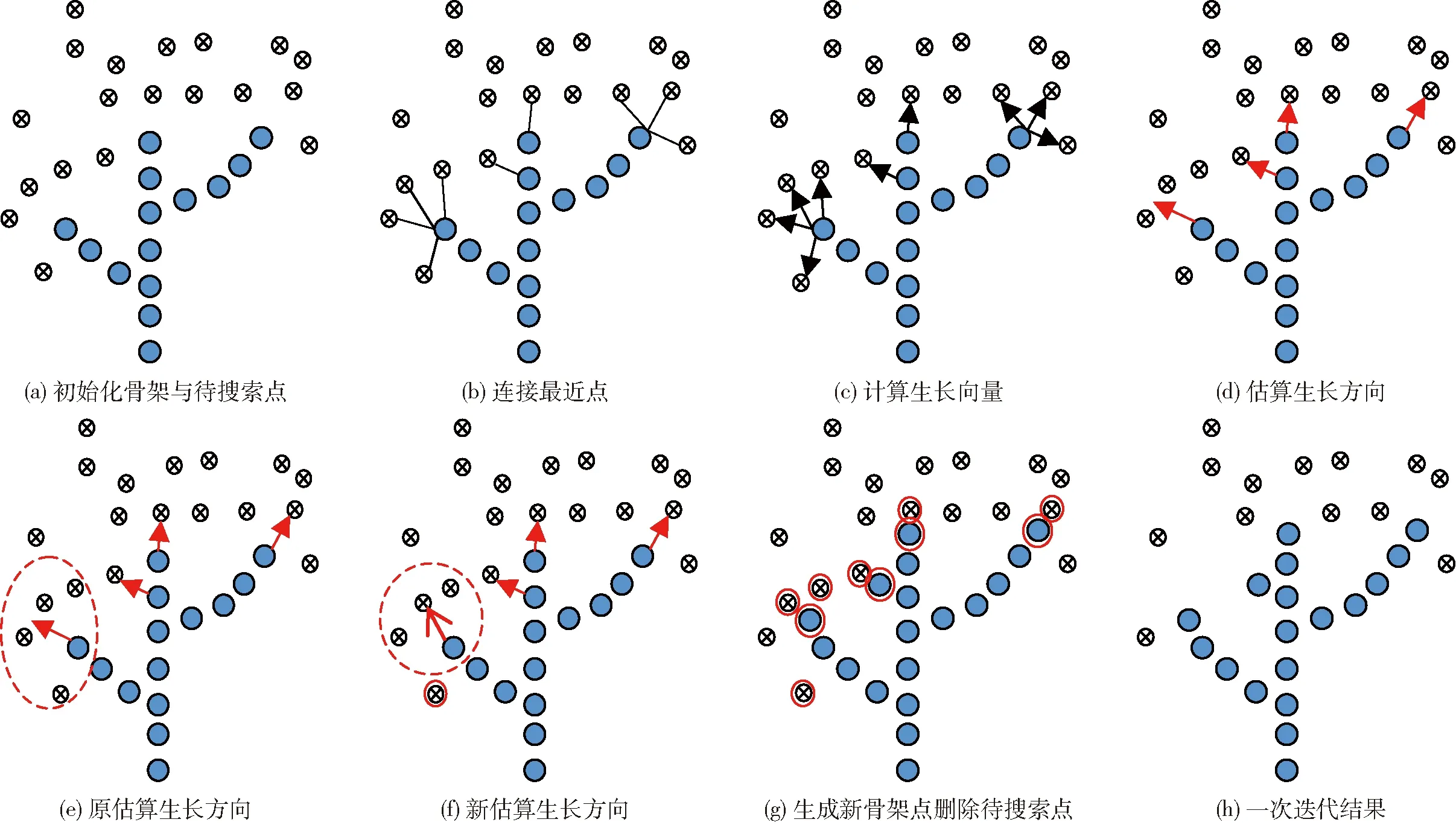
图5 改进后空间殖民算法过程Fig.5 Process of improved space colonization algorithm
(1)初始化树骨架数组,存储树骨架坐标,设定搜索半径Rs,将骨架点p搜索半径内的待搜索点存入集合S(p),如图5a所示。一个待搜索点只能影响距离最近的骨架点p,骨架点p可以同时受多个搜索半径内的待搜索点影响。具体数学关系为
(2)
式中q——距骨架点p小于搜索半径Rs的点集
(2)估算生长方向。将骨架点与所有能够影响骨架点的待搜索点相连,如图5b所示,计算方向向量,如图5c中的黑色箭头所示,将方向向量之和作为骨架的生长方向,并归一化,如图5d所示。具体数学关系为
(3)
式中d——方向向量
n——归一化结果向量
(3)将估算出的骨架生长方向与方向向量作夹角对比,若夹角大于60°,则删除此待搜索点后重新进行生长方向估算,如图5e、5f所示。具体数学关系为
(4)
式中t——生长向量
如图6所示,l1与l2是估算出的生长方向,引入角度约束后,有效的生长向量需在以估算生长方向为中心的60°圆锥体内。
(4)确定新骨架点位置。设定骨架点间距为Dp,则新骨架点Pj的位置为
Pj=Dpn
(5)
(5)删除待搜索点。设定删除阈值Rd,若空间待搜索点与新骨架点的距离小于删除阈值,则将待搜索点删除。如图5g所示,红色实线圆圈内为新生成的骨架点,红色虚线圆圈内为将要删除的点。具体数学关系为
|q-Pj|≤Rd
(6)
(6)开始下次迭代,直至所有的骨架点搜索不到待搜索点,即S(p)为空时。
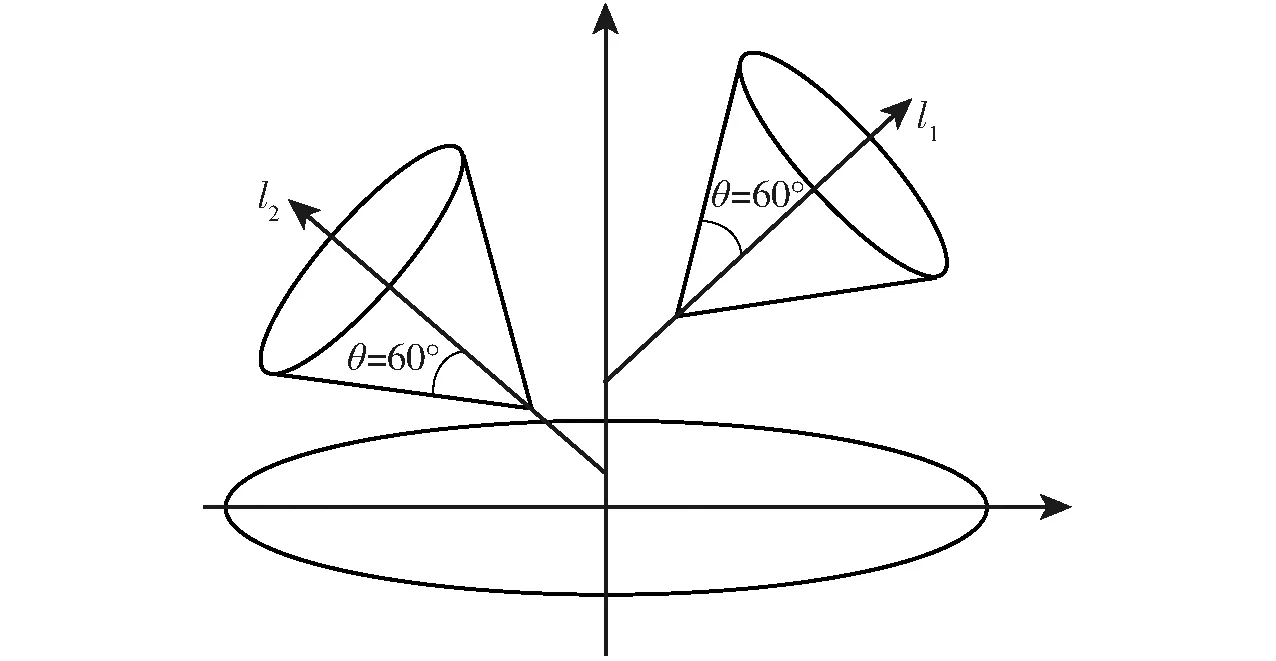
图6 角度约束Fig.6 Angle constraint
图5h为算法一次迭代后的结果。可以看到,中间主干继续向上生长,2条大侧枝斜向上生长,生成了一条新的侧枝,删掉了6个待搜索点,准备下一轮迭代。

图7 不同树种重构结果对比Fig.7 Comparisons of reconstruction results with different trees
图5e、5f中,左侧的侧枝生长方向原来受4个点影响,但是估算出的生长方向与其中一个生长向量(图5b小虚线框内的点)夹角超过60°,故舍去,新的估算方向如图5f中红色加粗箭头所示。对比图5e与图5f,加入生长角度约束后,新骨架的方向与原方向有较大不同,产生了不同的骨架走向,具体的算法描述如下:
定义骨架点集合;
定义待搜索点集合;
定义骨架点对应的可生长点集合S(p),并初始化;
whileS(p)不为空 do
for all 迭代骨架点 do
以骨架点p为球心,遍历搜索半径Rs内的点,将满足式(1)的点添入集合S(p);
end while
for all 迭代骨架点 do
根据式(3)估算骨架的生长方向n;
for all 迭代待搜索点 do
根据式(4)剔除不满足生长角度约束的生长向量;
重新估算生长方向;
end for
根据式(5)确定新骨架点坐标;
end for
for all 新骨架点 do
根据式(6)删除距离小于阈值Rd的点;
end for
将新骨架点坐标加入骨架点集合;
end while
采用上述算法经过多次迭代即可生成树点云对应的三维骨架,如图7b所示。
2.2 树干生成
树干使用多段连续的广义圆柱体基于提取到的骨架数据生成。将树的最粗主干称为1级枝干,在1级枝干上生出的侧枝称为2级枝干,在2级枝干上生出的枝干称为3级枝干,以此类推,树干的粗度变化遵循由根部到末端枝叶逐渐变细的规则,即由1级向2、3级逐渐变细的规律,在确定树枝的骨架后,树干的几何模型采用多段圆柱体连接表示,但圆柱的2个底面半径即树的粗度还未确定。日本学者SHINOZAKI等[24]提出的管道模型(Pipe model)在对树枝粗度估计上应用广泛。管道模型中,树枝分叉处的主枝与侧枝的父子关系定义为
(7)
式中rchild1、rchild2——子树枝的半径
rparent——父树枝的半径
i——指数

图8 叶片建模过程Fig.8 Process of leaf modeling
指数i一般取2[25]。对于树的最末端点,假设所有端点半径为常数r0,本文使用50分度游标卡尺实测后取值为0.3 cm,根据式(7),自顶向下计算得到所有树枝粗度。在获取树骨架完整信息与粗度信息后,沿骨架走向分段连续绘制圆柱体,根据文献[24-25]中的方法,将父级树枝圆柱体结束绘制的方向作为子级树枝起圆柱体开始绘制的方向,最终得到的枝条模型如图7c所示。
2.3 树叶添加
由于使用Kinect 2.0获取到的点云稀疏,很难从点云中直接重构树叶,因此对树叶单独建模,采用基于植物学规则的方法添加树叶。
叶片建模采用本研究团队自制的三维扫描设备[26],获取树叶的稠密点云数据。叶片建模的具体步骤为:
(1)使用Statistical outlier removal滤波器对点云数据进行去噪处理,得到光滑的叶片点云,如图8a所示。
(2)使用体素化网格下采样[27]方法对点云数据进行精简,设置体素边长为3 cm,得到叶片的稀疏点云,如图8b所示。
(3)使用Delaunay三角剖分[28]对稀疏点云进行网格化处理,生成叶片模型,如图8c所示。
(4)为叶片模型添加纹理,得到最终模型,结果如图8d所示。
树叶添加基于植物学中的叶序规则实现。树木常见的叶序生长规则主要有对生、旋生、轮生、二列生等[29],本文中的试验对象玉兰树属旋生叶序,根据此规则将叶片的三维模型添加至树干[30]。图7d为添加叶片后的树重构效果。
3 重构试验与分析
重构试验在Windows 7操作系统平台下进行,使用Visual Studio 2013集成化开发环境、OpenGL库、点云库(Point cloud library, PCL)以及Matlab 2014b完成,计算机配置为CPU i5-3450 3.1 GHz,内存8 GB,显卡AMD Radeon HD 6700 Series。
3.1 重构试验
为验证本文方法的普适性与有效性,选取玉兰树、枫树以及深圳先进技术研究院公开的Limit Tree数据,使用本文提出的重构方法进行重构试验,结果如图7所示。
由于不同树种的特征不同,故根据不同树的特征进行多次试验后,取搜索半径为1.2 cm,生长角度为60°,删除阈值为0.4 cm,骨架点间距0.3 cm;末端枝条粗度,玉兰树取值为0.3 cm,枫树与Limit Tree取值为0.2 cm。
重构试验展示了从原始点云数据到最终三维树模型重构的过程(图7a~7d)。图7b、7c中,由于点云局部不平滑,骨架上的部分地方会有不合理的细枝生成,出现“毛刺”现象,在使用广义圆柱体绘制枝条模型时,对枝条做了平滑处理,删掉了一些长度短的细枝,使枝条模型更加光滑、真实。由图7e可以看出,重构出的树模型与原始点云吻合度高,逼真地展现了树的三维结构,骨架走向合理,很好的体现了树的拓扑关系。
3.2 生长角度约束分析
本文在RUNIONS等[23]提出的空间殖民算法基础上加以改进:首先,原算法侧重于展示原理,树冠的形状由用户输入,树冠内的点也是基于规则生成,并不是基于实测数据,因此真实感与实际相比有一定的差距,改进后,本文使用实测点云数据作为算法的输入。其次,在估算骨架生长方向时,加入了生长角度约束,减少了走向不合理的枝条出现。
以玉兰树为例,分别设定生长角度约束θ为45°、60°、75°以及无约束,对比效果如图9所示。从图9可以看出,生长角度从整体上约束了树枝的走向,在无角度约束时,部分枝条会出现向下生长和枝条开角过大的情况。加入角度约束后,不同角度对枝条的开角产生了不同的约束效果,随着角度约束的增大,枝条开角随之增大。当θ=45°时,枝条开角被约束在45°以内,呈收紧状态,当θ=75°时,图9d中红色虚线圆框内部分枝条出现了较大开角,走向不合理的情况,参照文献[29],角度约束设定为60°时,枝条开角与走向较为自然。

图9 不同角度约束下的树干模型对比Fig.9 Comparisons of branch model with different angle constraints

图10 不同算法骨架提取结果对比Fig.10 Comparisons of skeleton extraction results with different algorithms
3.3 骨架提取方法对比分析
将本文的骨架提取算法与L1-Medial算法[31]、Laplacian算法[32]进行对比,结果如图10所示。由图10可以看出,图10b中,L1-Medial算法可以正确地提取到树主干部分的骨架,但是无法展现冠层内的骨架细节,在提取玉兰树骨架时,出现了明显的断节,生成了孤立骨架,在提取枫树与Limit Tree骨架时,出现了走向不合理与交叉连通现象;图10c中,Laplacian算法整体效果比L1-Medial算法稍好,但是骨架不连续的情况严重,细枝骨架走向凌乱,尤其在冠层点云稠密处,骨架交叉严重,与实际情况出入大;图10d中,本文骨架提取方法有多余短枝出现,但是骨架连续,无交叉,冠层内细枝骨架清晰,走向合理,较为真实地展现了树的骨架结构,可为树的虚拟修剪等研究提供数据支持[33]。
3.4 重构误差分析
为评价重构模型的精度,选取树高、主干粗度、冠幅3个参数,将实测数据与模型数据做对比,统计相对误差,如表1所示。为分析枝干拓扑结构的误差,使用50分度游标卡尺,每棵树随机选取6条枝干实地测量其直径,其中2、3、4级枝干各取2枝,依次编号为b21、b22、b31、b32、b41、b42,以实测值作为基准值,统计相对误差,如表2所示。

表1 树模型参数Tab.1 Parameters of reconstructed tree models
注:主干粗度统一取距离地面0.5 m处树干直径。
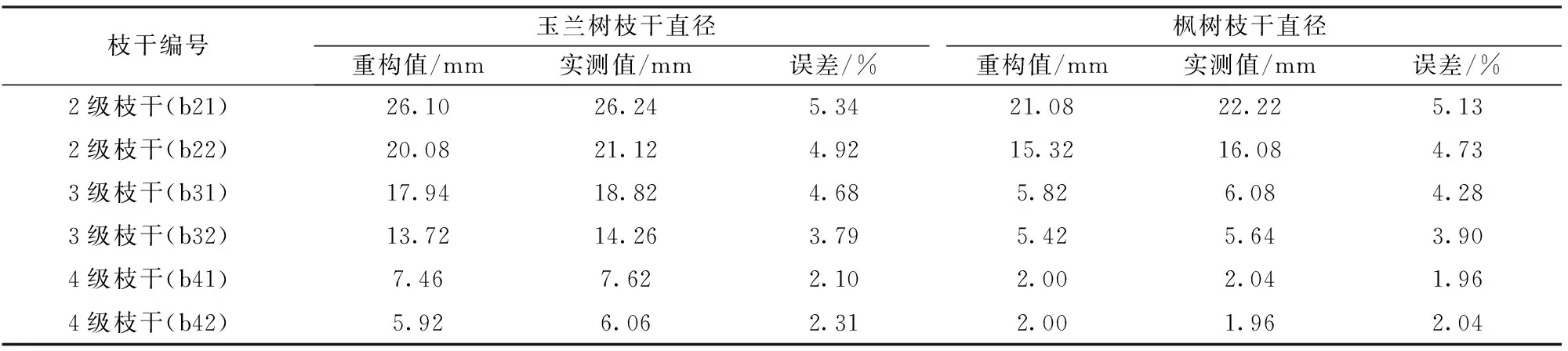
表2 分级枝干模型参数Tab.2 Parameters of different levels branch models
表1数据表明,重构出的玉兰树与枫树模型在树高与冠幅参数上面误差较小,均在3.5%以内,在主干粗度参数上误差较大,但是没有超过6.5%。分析其原因,本文基于实测点云数据重构,重构模型最小包围盒的高度与宽度十分接近真实树的树高与冠幅,而主干的粗度依据管道模型估算得出,因此误差相对较大。
表2数据表明,随着枝干级数的增加,误差也随之累积,但是总体误差在6%以内,同一级别枝干,枫树的误差略小于玉兰树,分析其原因,由于2棵树复杂程度不同,所以构建出的树模型层级结构不同,在树枝的分叉处,基于管道模型理论,使用式(7)估计父级枝干与子级枝干的粗度关系,并且由子级向父级逐级传递,使误差不断累积,但是总体误差控制在6%以内,说明了管道模型粗度估计的合理性,可以较为精确地构建树模型,展现枝干的拓扑结构。
4 讨论
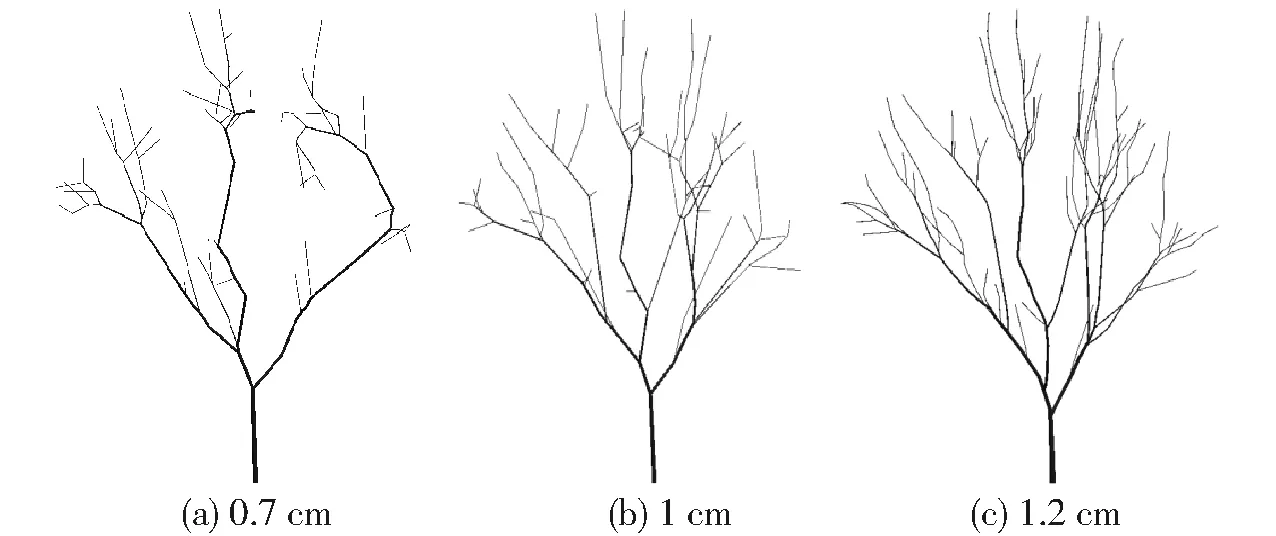
图11 不同搜索半径对比结果Fig.11 Comparison results of different search radii

图12 不同删除阈值对比结果Fig.12 Comparison results of different delete values

图13 不同骨架点间距对比结果Fig.13 Comparison results of different skeleton node distances
算法中的“搜索半径”、“生长角度”、“删除阈值”、“骨架点间距”和“树枝粗度”5个参数决定了树的最终形态结构。不同参数值的选择不仅对生成的树形外观有影响,同时对骨架点的数量、生成树枝的数量有影响。搜索半径决定了每次迭代时骨架点生长方向的候选点的多少,即集合S(p)的大小。搜索半径的取值对树的最终形态有着较大影响,若搜索半径过小,算法每次迭代时,待搜索范围过小,会使生长方向朝向局部密集处,枝干出现不合理的走向,若搜索半径过大,待搜索点过多,会在一定程度上违背“就近影响”的原则,导致生成一些多余的细枝。图11展示了不同搜索半径下的对比结果。删除阈值对骨架提取影响较大,这一参数主要是为了避免待搜索点对骨架走向的重复影响,其值将影响树枝的数量,若取值过小,冠层内的点会重复影响骨架的走向,细枝会明显增多,呈现出多节现象,若取值过大,待搜索点没有影响骨架的走向就被删掉,生成的枝条稀疏,与实际出入较大,真实感低。图12展示了不同删除阈值下的对比结果,可以看出随着删除阈值的增加,细枝在不断减少,骨架结构的细节展示越来越差。生长角度约束了骨架的大体走向,使树木整体向上生长,但并不适用于柳树等枝条下垂的树种。骨架点间距与生长方向共同决定了新骨架点的位置。图13展示了不同骨架间距下的对比结果,从中可以看出,若骨架间距太小,会使骨架生长速度过慢,在删除阈值的影响下,骨架点附近的点会被删除,使迭代过早结束,无法生成完整的骨架;若骨架点间距过大,骨架生长呈跳跃式,使枝干过于僵硬,骨架点之间的待搜索点会影响主骨架成为侧枝,会出现细枝过多的情况。在树枝的最末端点枝条粗度值选择上,由于本文的玉兰树树高为2.5 m,可人工测量,为粗度取值提供依据,若试验对象为高大的树种无法获取末端枝条粗度时,需进行预估后不断测试,找到合理的末端枝条粗度。
5 结论
(1)以RUNIONS等提出的空间殖民算法为基础,本文空间殖民算法中,冠层生长空间用输入的点云数据表示,树冠的形状也由输入点云决定,与原算法基于规则相比,提高了重构模型的精度。
(2)基于实测点云数据,引入生长角度约束对原空间殖民算法进行改进,对原始点云数据经过去噪、配准等预处理后,作为算法的输入,提取树的三维骨架信息,在重构试验中,将本文骨架提取算法与L1-Medial算法、Laplacian算法做对比分析,验证了本文算法的合理性与有效性;在三维骨架生成过程中保存骨架点的顺序,根据管道模型获得枝条的粗度信息,使用广义圆柱体生成树的枝干,对叶片单独建模并按照叶序规则添加树叶,最终生成树的三维模型。
(3)算法给出了5个可调参数,以实测点云数据为依据,用户可以通过调节参数控制树的形态,得到与真实数据吻合的结果,重构误差在6.5%以内,重构模型可为树冠层光照分析、剪枝等提供参考。
1 赵春江,陆声链,郭新宇,等. 数字植物研究进展:植物形态结构三维数字化[J]. 中国农业科学, 2015, 48(17):3415-3428.
ZHAO C J, LU S L, GUO X Y, et al. Advances in research of digital plant: 3D digitization of plant morphological structure[J]. Scientia Agricultura Sinica, 2015,48(17):3415-3428. (in Chinese)
2 张建,李宗南,张楠,等. 基于实测数据的作物三维信息获取与重建方法研究进展[J]. 华中农业大学学报, 2013,32(4):126-134.
ZHANG J, LI Z N, ZHANG N, et al. Advances in 3D information collection and reconstruction of crop based on the measured data[J]. Journal of Huazhong Agricultural University, 2013,32(4):126-134. (in Chinese)
3 HONDA H. Description of the form of trees by the parameters of the tree-like body: effects of the branching angle and the branch length on the shape of the tree-like body[J]. Journal of Theoretical Biology, 1971,31: 331-338.
4 PRUSINKIEWICZ P, LINDENMAYAR A. The algorithmic beauty of plants[M].New York:Springer-Verlag Press, 1990.
5 LINERMANN B, DEUSSEN O. Interactive modeling of plants[J]. IEEE Computer Graphics and Application, 1999, 13(1): 56-65.
6 OKABE M, OWADA S, IGARASHI T. Interactive design of botanical trees using freehand sketches and example-based editing[J]. Computer Graphic Forum, Proceeding of Eurographics, 2005, 24(3): 487-496.
7 WITHER J, BOUDON F, CANI M P, et al. Structure from silhouettes: a new paradigm for fast sketch-based design of tree[J]. Computer Graphic Forum, Proceedings of Eurographics, 2009, 28(2): 541-550.
8 QUAN L, TAN P, ZENG G, et al. Image-based plant modeling[J]. ACM Transactions on Graphics, 2006, 25(3): 599-604.
9 TAN P, ZENG G, WANG J, et al. Image-based tree modeling[J]. ACM Transactions on Graphics, 2007, 26(3): 87-93.
10 XU H, GOSSETT N, CHEN B. Knowledge and heuristic-based modeling of laser-scanned trees[J]. ACM Transactions on Graphics, 2007, 26(4): 19-31.
11 LIVNY Y, PRINK S, CHENG Z, et al. Texture-Lobes for tree modeling[J].ACM Transactions on Graphics, 2011, 30(4): 53-62.
12 XIE K, YAN F, SHARF A, et al. Tree modeling with real tree-parts examples[J]. IEEE Transactions on Visualization and Computer Graphics, 2016, 22(12): 2608-2618.
13 RUNIONS A, LANE B, PRUSINKIEWICZ P. Modeling trees with a space colonization algorithm[C]∥Proceedings of Eurographics WorkShop on Natural Phenomena, 2007: 63-70.
14 ZHANG X, LI H, DAI M, et al. Data-driven synthetic modeling of trees[J]. IEEE Transactions on Visualization and Computer Graphics, 2014, 20(9): 1214-1226.
15 唐丽玉, 张浩, 黄洪宇, 等. 基于点云数据的树木三维重建方法改进[J/OL]. 农业机械学报, 2017, 48(2): 186-194. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170225&journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2017.02.025.
TANG L Y, ZHANG H, HUANG H Y, et al. Improved method for 3D reconstruction of tree model based on point cloud data[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(2): 186-194. (in Chinese)
16 姚远, 刘志刚. 基于 Kinect 的三维重建与点云雕刻的实现[J]. 现代制造工程, 2017(4): 128-132.
YAO Y, LIU Z G. 3D-object reconstruction and point cloud sculpture based on Kinect[J]. Modern Manufacturing Engineering, 2017(4): 128-132. (in Chinese)
17 YANG L, ZHANG L, DONG H, et al. Evaluating and improving the depth accuracy of Kinect for Windows v2[J]. IEEE Sensors Journal, 2015, 15(8): 4275-4285.
18 袁华, 庞建铿, 莫建文. 基于噪声分类的双边滤波点云去噪算法[J]. 计算机应用, 2015, 35(8): 2305-2310.
YUAN H, PANG J K, MO J W. Denoising algorithm for bilateral filtered point cloud based on noise classification[J]. Journal of Computer Applications, 2015, 35(8): 2305-2310.(in Chinese)
19 RUSU R B, MARTON Z C, BLODOW N, et al. Towards 3D point cloud based object maps for household environments[J]. Robotics and Autonomous Systems, 2008, 56(11): 927-941.
20 GENG N, MA F, YANG H, et al. Neighboring constraint-based pairwise point cloud registration algorithm[J]. Multimedia Tools and Applications, 2016, 75(24): 16763-16780.
21 姚吉利. 3维坐标转换参数直接计算的严密公式[J]. 测绘通报, 2006(5):7-10.
YAO J L. Rigorous formula for direct calculating parameter in 3D transformation[J]. Bulletin of Surveying and Mapping, 2006(5):7-10. (in Chinese)
22 YU X, SONG H, WANG S. Capture of multi-view point clouds and registration of plants based on Kinect[J]. International Agricultural Engineering Journal, 2016, 25(1):74-84.
23 RUNIONS A, OUHRER M, LANE B, et al. Modeling and visualization of leaf venation patterns[J]. ACM Transactions on Graphics, 2005, 24(3): 702-711.
24 SHINOZAKI K, YODA K, HOZUMI K, et al. A quantitative analysis of plant form-the pipe model theoryⅠ. basic analyses[J]. Japanese Journal of Ecology, 1964, 14(3): 97-105.
25 SHINOZAKI K, YODA K, HOZUMI K, et al. A quantitative analysis of plant form-the pipe model theory Ⅱ. further evidence of the theory and its application in forest ecology[J]. Japanese Journal of Ecology, 1964, 14(4): 113-139.
26 ZHANG Z Y,YUAN L. Build a 3D scanner system based on monocular vision[J].Applied Optics,2012,51(11):1638-1644.
27 朱德海.点云库PCL学习教程[M]. 北京:北京航空航天大学出版社,2012.
28 杨军,林岩龙,李龙杰,等. 基于快速Delaunay三角化的散乱点曲面重建算法[J]. 计算机工程与科学,2015,37(6):1189-1195.
YANG J, LIN Y L, LI L J, et al. A surface reconstruction algorithm for unorganized points based on fast Delaunay triangulation[J]. Computer Engineering & Science, 2015,37(6):1189-1195. (in Chinese)
29 张志翔. 树木学[M].2版. 北京:中国林业出版社,2010.
30 胡少军,耿楠,张志毅,等. 基于稀疏图像的真实树交互建模方法[J]. 农业工程学报,2014,30(9): 168-175.
HU S J, GENG N, ZHANG Z Y, et al. Interactive modeling of outdoor trees based on spare images[J]. Transactions of CSAE, 2014, 30(9): 168-175. (in Chinese)
31 HUANG H, WU S, COHEN-OR D, et al. L1-medial skeleton of point cloud[J]. ACM Transactions on Graphics, 2013, 32(4): 65:1-65:8.
32 AU O K C, TAI C L, CHU H K, et al. Skeleton extraction by mesh contraction[J]. ACM Transactions on Graphics (TOG), 2008, 27(3): 44.
33 王丹, 邵小宁, 胡少军, 等. 基于 Kinect 的虚拟果树交互式修剪研究[J]. 农机化研究, 2016,38(10): 187-192.
WANG D, SHAO X N, HU S J, et al. Interactive pruning operation on virtual fruit tree based on Kinect[J]. Journal of Agricultural Mechanization Research, 2016,38(10): 187-192. (in Chinese)
