基于有限元方法的阶梯形超声变幅杆的设计与修正
2018-03-12王忠进缪兴华胡神阳汪炜
王忠进,缪兴华,胡神阳,汪炜
(南京航空航天大学机电学院,江苏南京210016)
超声变幅杆在超声技术、特别是功率超声设备的振动系统中有着举足轻重的地位,其主要作用是将机械振动的质点位移或速度放大,或将超声能量集中在较小的面积上,即具有聚能作用[1]。由于超声换能器的输出振幅只有几微米,但在功率超声加工领域所需振幅要达到几十甚至几百微米,所以换能器必须和变幅杆配合,才能输出所需的振幅。
按照振动方向可将变幅杆分为纵向振动、弯曲振动、扭转振动三大类。其中,纵向振动变幅杆可分为简单形和复合形,简单形又可分为指数形、圆锥形、悬链形及阶梯形,复合形则是由各种简单形变幅杆根据实际需要组合而成的[2]。变幅杆的设计方法主要有解析法和等效电路法,其计算量较大,且结果存在误差[3]。本文采用解析法设计变幅杆,使用CRO/E建立三维模型,并运用ANSYS Workbench对变幅杆进行模态分析[4],同时对阶梯形变幅杆频率修正的过程进行仿真分析,根据修正的仿真结果指导修正过程,以此提高修正效率。
1 变幅杆的理论分析与设计
1.1 变截面杆纵振动的波动方程
某变截面杆见图1。假设变幅杆是由均匀且各向同性的材料构成,不计机械阻抗,且横截面上各点所受的应力均匀。其对称轴为坐标轴x,作用在小体元(x,x+dx)所限定的区间上的张力为dx,根据牛顿定律可写出动力学方程为[1]:
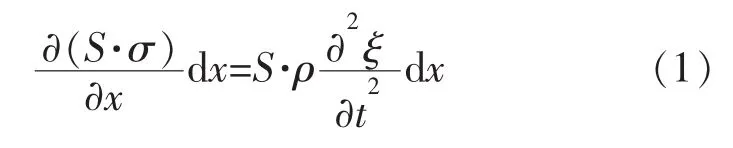

图1 变截面杆的纵振动
式中:S=S(x)为杆的横截面积函数;ξ=ξ(x)为质点位移函数为应力函数;ρ为变幅杆的材料密度;E为杨氏模量。
在简谐振动的情况下,式(1)可写成:
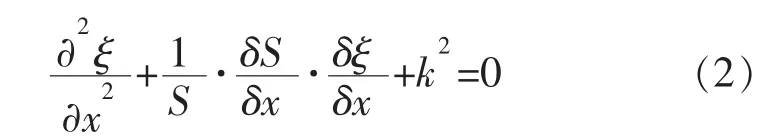
式中:k2=w2/c2。其中,k为圆波数;w为圆频率;c为纵波在细棒中的传播速度式(2)即为变截面杆纵振动的波动方程。
1.2 阶梯形变幅杆的理论分析
如图2所示,阶梯形变幅杆由两段不同截面积的均匀杆组成,其中直径较大的一端为大端,直径较小的一端为小端,以下统一简称为大端、小端。
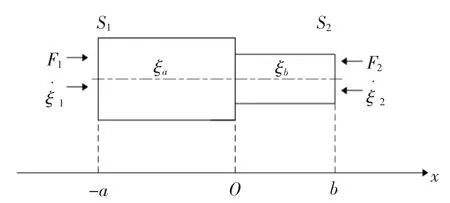
图2 变幅杆示意图
由此可得到均匀截面杆的波动方程为:

式为:
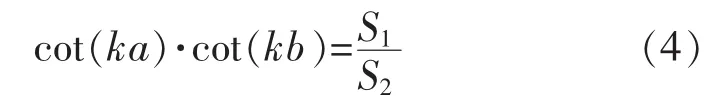
1.3 阶梯型变幅杆的设计
为实现整个超声振动系统的共振,变幅杆的固有频率应与换能器的谐振频率一致,即尺寸必须满足频率方程,变幅杆的设计频率为整个振动系统的设计频率。
1.3.1 超声变幅杆和工具头的材料选择
超声变幅杆的材料特性决定其传振效果和放大倍数,要求材料在振动时的损耗小、疲劳强度高,且声阻抗和工具头、换能器匹配。符合上述要求的金属材料有钛合金、45钢、铝合金、铜镍合金等。其中,钛合金的性能较好,但机械加工较困难,价格相对较贵,故一般选用45钢、铝合金等材料。考虑到超声波在不同介质中传播声阻抗匹配,能量损耗较多,且换能器前盖板采用铝合金研制,故选用硬铝作为超声变幅杆的材料;考虑到工具头在加工过程中磨损严重,故选择模具钢作为工具头的材料。变幅杆、工具头的材料性能参数见表1。
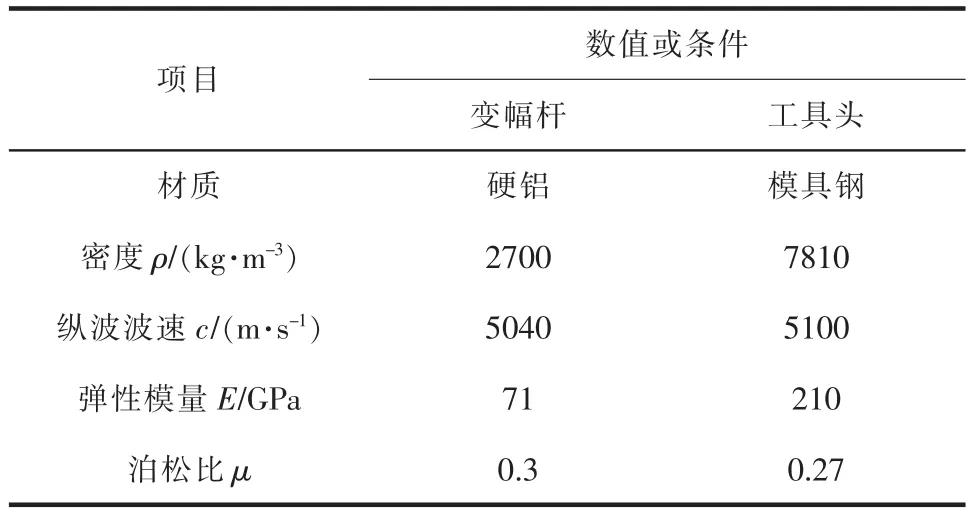
表1 材料性能参数表
1.3.2 变幅杆尺寸计算
设计变幅杆的工作频率为28 kHz、大端直径D1=25 mm、小端直径D2=15 mm。如图3所示,变幅杆总长为波长的二分之一,其中波长λ为:

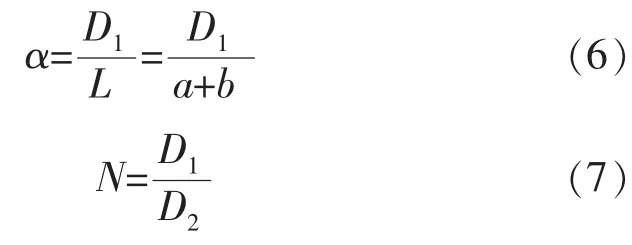
由式(6)、式(7)可得α=0.5、N=1.67,通过查手册可知过渡圆角R取值5 mm[2]。
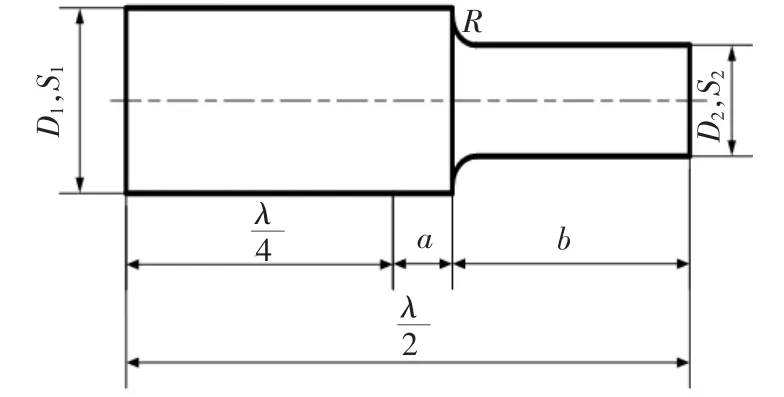
图3 变幅杆设计示意图
1.3.3 工具头对变幅杆的影响
在设计工具头时,可将其看作直径为15 mm、长度为14 mm的圆柱体。由于工具头的直径小于波长的十分之一(15 mm<18 mm),长度小于波长的四分之一(14 mm<45 mm),因此,在设计阶段可根据公式计算工具头的等效质量,以减小设计任务的复杂性。如图4所示,根据机电类比[5-7]:
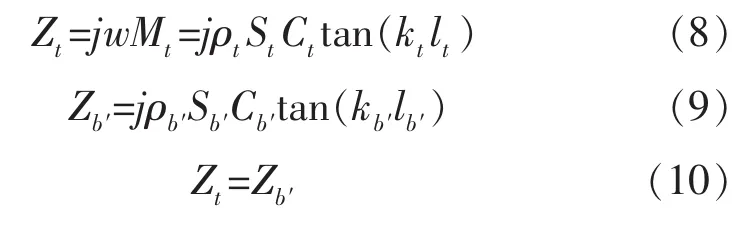
由此可得lb′=28 mm。则b′=b-lb′=12 mm。因此,变幅杆大端长度为55 mm,小端长度为12 mm,过渡圆角R=5 mm。
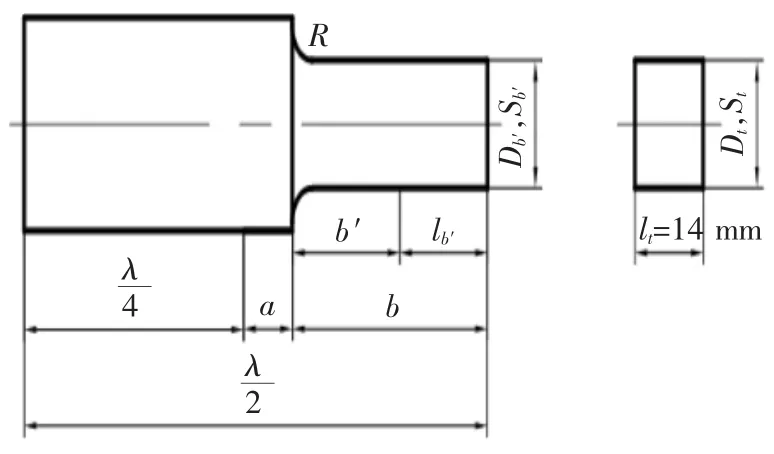
图4 工具头对变幅杆谐振频率的影响示意图
2 超声变幅杆的有限元分析
为了验证微细超声振动系统设计的合理性,采用ANSYS Workbench 15.0仿真分析软件对变幅杆和工具头进行模态分析,主要用于确定变幅杆和工具头的固有频率及振型。具体分析步骤为:①建立有限元模型,设置材料特性;②定义接触区域;③定义网格控制并划分网格;④施加载荷与边界条件;⑤定义分析类型;⑥设置求解频率选项;⑦对问题进行求解;⑧对结果进行评价分析,具体表现为确定谐振频率及振型。
根据上述设计尺寸,在CRO/E软件中对超声变幅杆及工具头进行三维建模,并将其导入ANSYS中,利用自动网格划分功能对变幅杆和工具头进行网格划分[8],结果见图5。
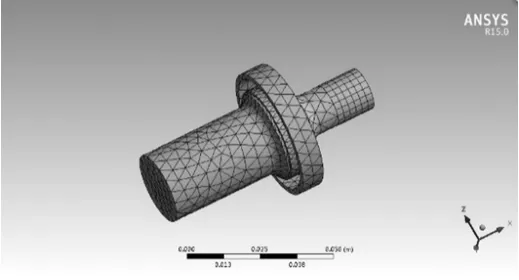
图5 超声变幅杆和工具头的网格划分模型
设置模态分析的频率范围为20~80 kHz,共求得6个谐振频率。在模态分析时,假设工具头和变幅杆不承受任何载荷;在装夹时,仅对变幅杆节面处的圆周面进行固定。所设计的工具头和变幅杆的谐振频率为28 kHz,由图6可知,与之最接近的频率为28.206 kHz[9]。由此可得出结论:在此频率下,变幅杆和工具头处于厚度方向振动状态,即设计对应的振型为纵振模式,该仿真结果与理论设计的偏差为0.736%。同时还可看出,端面的输出振幅最大,设计节面位置的位移为零,满足设计要求。
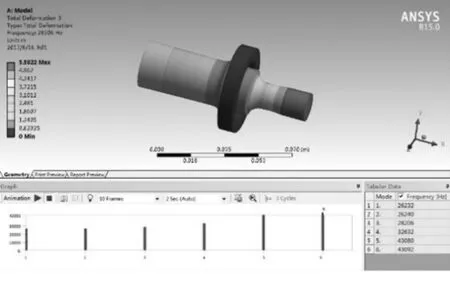
图6 谐振频率分析结果
3 超声变幅杆的修正
由于存在加工误差,加上变幅杆的材料金相组织分布不均匀且含有杂质等原因,使制作出的变幅杆频率与设计的理论值不符,故需对变幅杆加以修正,使其达到加工所需的值。利用阻抗分析仪检测得到变幅杆的谐振频率为26.423 kHz。为了提高修正效率,改变变幅杆三维模型的大、小端的长度并对其进行仿真,利用仿真结果指导修正过程。
由图7~图10所示仿真结果可知,变幅杆大端长度减少1 mm,频率增加232 Hz,长度减少2 mm,频率增加459 Hz;变幅杆小端长度减少1 mm,频率增加304 Hz,长度减少2 mm,频率增加785 Hz。由此可得,在修正过程中,变幅杆小端长度变化对频率得影响比大端长度变化影响大,所以大端的修正尺寸应比小端修正尺寸更大;且在相同条件下,为保证频率的变化更稳定,应先修大端、再修小端。
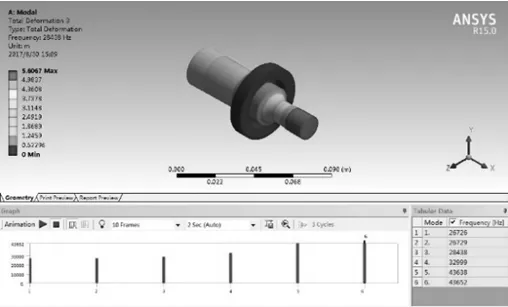
图7 大端长度减少1 mm的仿真结果
在上述结论的指导下,本文对变幅杆进行了修正。表2是修正过程中的变幅杆频率变化情况,数据显示,大端长度修正2 mm,频率增加493 Hz;小端长度修正1.5 mm,频率增加585 Hz,证明了小端长度变化对频率影响较大的结论。同时,通过先对变幅杆大端长度修正2 mm得到了变幅杆频率变化的大致范围,并利用其确定了小端长度修正1 mm时,变幅杆频率不高于28 kHz,从而无需再进行新的修正,大幅提高了效率。在对变幅杆长度进行反复修正后,振动系统的谐振频率逐渐向设计值靠拢,最终达到27.865 kHz,满足了设计要求。
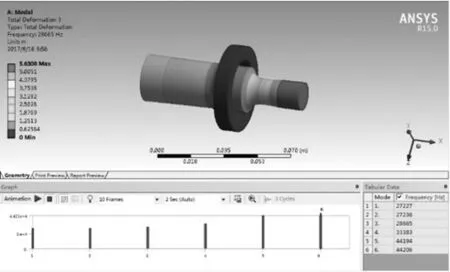
图8 大端长度减少2 mm的仿真结果
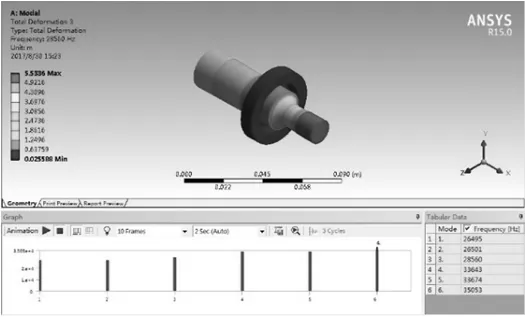
图9 小端长度减少1 mm的仿真结果
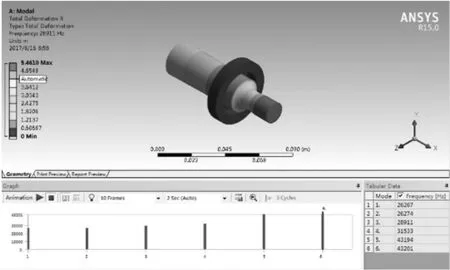
图10 小端长度减少2 mm的仿真结果
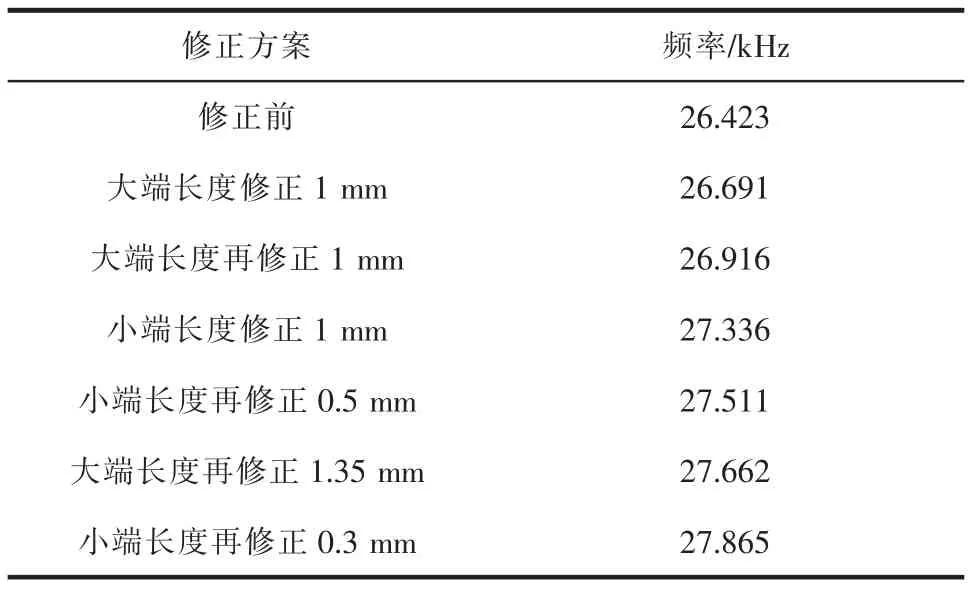
表2 变幅杆修正过程及其结果
4 结束语
本文设计、制作、修正了一个阶梯形的变幅杆,使其符合设计要求。通过ANSYS有限元分析软件对该阶梯形变幅杆的频率修正过程进行仿真分析,可确定先修正大端还是小端,并根据修正大端变幅杆谐振频率变化的情况,估算出修正小端长度时的谐振频率变化范围,减少在修正小端长度时的尝试性修正,大幅提高了修正效率。
[1] 林仲茂.超声变幅杆的原理及设计[M].北京:科学出版社,1987.
[2] 曹凤国.超声加工技术[M].北京:化学工业出版社,2004.
[3] 高洁.超声变幅杆的优化设计及声学特性分析[D].西安:陕西师范大学应用声学研究所,2006.
[4] 朱寅.超声变幅杆有限元谐振分析[J].机械,2005,32(12):13-15.
[5] 丁瑞翔,汪炜,张永俊,等.基于负载阻抗的固结磨料超声加工自动进给设计与试验[C]//第16届全国特种加工学术会议论文集(下).厦门,2015:441-446.
[6] COATESR,MATHAMSRF.Designofmatching networks for acoustic transducers[J].Ultrasonics,1988,26(2):59-64.
[7] KLEESATTEL C.Uniform stress contours for disk and ring resonators vibrating in axially symmetric radial and torsional modes[J].Acta Acustica united with Acustica,1968,20(1):1-13.
[8] 薛庚健,马麟,李亚洁.阶梯形超声变幅杆的设计分析[J].机械设计与制造,2013(12):14-16.
[9] 贾杨,沈建中.阶梯形变幅杆的频率特性分析[J].声学技术,2006,25(2):154-159.
