各省市碳排放强度核算及其空间相关性分析
2018-03-12
(同济大学经济与管理学院 上海 200092)
一、引言
碳元素是地球上构成生命的必不可少元素之一,人类体重约有五分之一都是碳元素。温室气体中二氧化碳(CO2)中碳元素含量为12/44,是碳元素的主要存在形式之一。人类新陈代谢过程中会呼出二氧化碳,而植物、藻类和细菌等能够通过光合作用,吸收二氧化碳进而转化为碳水化合物。《京都议定书》指出主要的温室气体有二氧化碳(CO2)、甲烷(CH4)、氧化亚氯(N2O)、氢氟碳化物(HFCS)、全氟化碳(PFCS)、六氟化硫(SF6)六种,其中二氧化碳是最主要排放气体,占温室气体排放总量的60%,而且由于二氧化碳具有的“惰性”使得其无法利用化学作用予以消除,所以减少二氧化碳排放量是应对气候变暖的唯一途径。碳排放(carbon emission)是二氧化碳和其它温室气体排放的总称。根据再生性分为可再生碳排放和不可再生碳排放两种。可再生碳排放包括保证地球表面存在的生命体运转的碳循环以及消耗可再生能源所产生的碳排放。不可再生碳排放主要指的化石能源碳排放,化石能源是经过几亿年的沉积才能形成的,具有不可再生性。可见,后者的碳排放对人类生存环境以及发展有更大的危害。基于二氧化碳在温室气体排放的主体地位,本文研究对象仅为CO2排放情况,不考虑其他温室气体。
二、碳排放强度核算
核算碳排放总量是进行碳排放研究的基础,本文基于各省市的能源平衡表,对于不同能源种类分别核算其排放量并进行加总,具体公式如下所示。其中,cei表示碳排放强度,表示该省市的碳排放总量,为该省市实际GDP,本文选取2000年为基年进行平减。
(3.1)
对于省市碳排放的核算,主要基于各省市能源平衡表中化石燃料消费量,数据来源于中国统计年鉴、中国能源统计年鉴。其优点在于官方数据普遍得到认可,且收集所需时间相对较少,成本较低,能够满足本文对于省域范围内碳排放量的简单核算的要求。本文基于《能源消耗引起的温室气体排放计算工具指南(2.1版)》中所列示的二氧化碳排放因子,分别对不同能源的碳排放量进行核算病假总,具体计算公式如下,其中j表示各省市消耗的不同能源品种:
CO2emission=∑化石燃料消费量j×CO2排放因子j
(3.2)
我们采用的上文的方法,计算了中国大陆30个省区市(西藏除外)的碳排放强度数据,并将其以地图的形式呈现出来,如图1所示,其分别为中国省区2003年及2015年的碳排放强度分布。本文由于篇幅限制仅选取了研究区间首尾两年年进行展现。
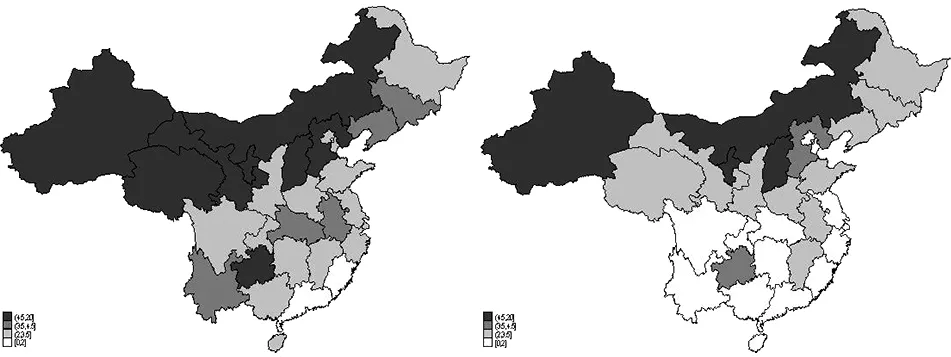
图1 2003和2015年碳排放强度分布图
中国自改革开放以来,一直秉持着区域区别发展战略,行政划分为东部沿海、中部及西部内陆三块区域,从省市碳排放强度的分布上,我们可以看到区域碳排放强度水平与区域社会经济发展梯度发展模式有密切联系,总体上表现为西高东低、北高南低的特征,即西北地区和西南地区高,中东部地区低,东部沿海地区明显低于全国平均水平。究其原因,可能是因为东部沿海地区经济发达、社会发展水平高,且在区域经济发展具有较强的空间集聚效应,从而产业结构较为合理,碳排放强度就较低;西北地区为主要能源输出区域,碳排放强度高;西南地区则由于社会经济发展落后于东部地区,碳排放强度相比东部沿海地区也稍显较高。
对于所选取的两年中,均处于最高排放强度区间的省市有:新疆、内蒙古、山西、宁夏;均处于最低排放强度区间的省市有:福建、广东。随着时间的变化,其他各省市的碳排放强度也发生了一定的变化,但全国总体上呈现出下降趋势。
三、空间相关性分析
其次,检验空间相关性及运用空间计量模型还需确定空间权重矩阵形W。空间权重矩阵选择问题一直是空间计量经济学中的一个难题,权重矩阵的选择正确与否关系到模型的最终估计结果。本文首先对已有研究中一般空间权重矩阵的设定方法做出简要介绍,并提出本文的设定方法与合理性。具体说明如下:
一般空间权重矩阵为目前研究使用最为广泛的一种设定方法,即相邻省市给予的权重为1,而非相邻的省市给予权重为0。一般空间权重矩阵有其自身的优点。首先,权重设置非常简便,根据中国各省市的地理位置便可轻松设置,而不用考虑过多的其他因素,即本文以中国内陆30个省市(除西藏外)为研究主体,共计65对相邻省市①。被给予权重1,其余均为0;其次,全国30个省份在空间分布上具有连续性,且省级行政单元地理范围较广,中心坐标所处地理位置不能完全代表该省实际碳排放产生的源头;最后,由于我国国情实行区域化管理,如行政区域划分为东、中、西部地区,政策的实施也参考行政区域的划分,因此采用临近原则更容易从行政区域分析碳排放强度分布特点。
确定了了空间权重矩阵,便可考察各省市碳排放强度是否存在空间依赖性,目前文献中提出了常用度量空间自相关的方法,最为流行的是“莫兰指数I”(Moran’s I),其计算公式如下:
(3.6)
其中表示第i个省市的碳排放强度值,分别表示该年碳排放强度的均值和方差,n为地区总数(本位为30),为基于车相邻原则构建的空间权重矩阵。
莫兰指数I的取值一般介于-1到1之间,大于0表示正自相关,即高值与高值相邻、低值与低值相邻;小于0表示负自相关,即高值与低值相邻。如果莫兰指数I接近于0,则表明空间分布是随机的,不存在空间自相关。本文基于前文的所获得的数据、计算方法,分别在W权重下借助Stata计量软件得到2003-2015各年碳排放强度的全局莫兰指数及其显著性,如表1所示。
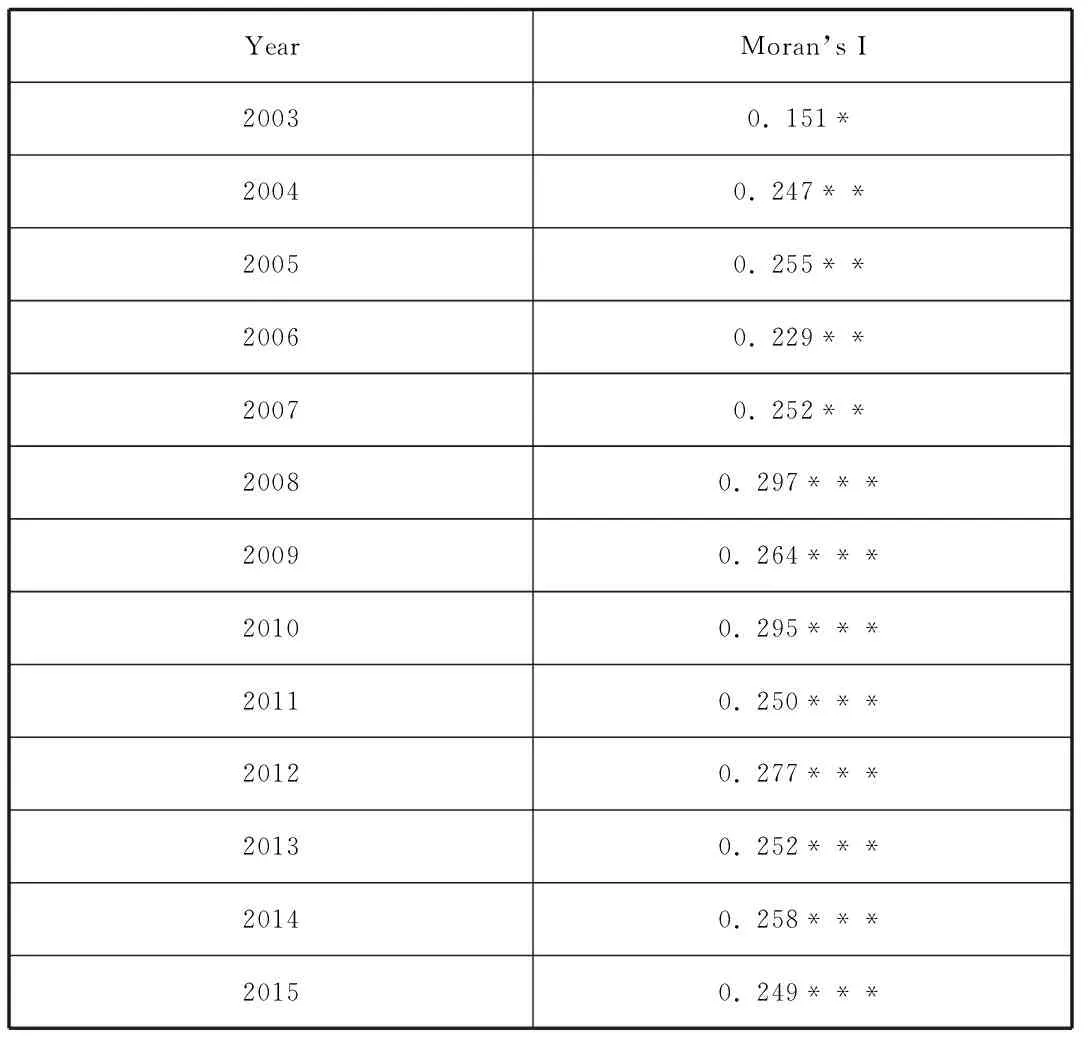
表1 2003-2015年我国各省间碳排放强度莫兰指数I
注:***,**,*分别表示在1%,5%和 10%水平上显著。
从上表可以看出,2003-2015年省际碳排放强度的全局莫兰指数I值在所有年份都显著为正,说明省际碳排放强度存在较强的空间正相关关系,某一地区碳排放强度会对其相邻地区的碳排放强度产生正向的影响。当然,也会受相邻地区碳排放强度的影响。引入综合空间权重矩阵与常规的一般空间权重矩阵相对比,即在考虑各省际间的地理距离和能源禀赋因素后,莫兰指数更大,碳排放强度的正相关性更强。
全局莫兰指数I只能从整体上描述省际碳排放强度空间相关性,而无法描述不同地区空间相关性的具体类型,莫兰散点图在这方面做了很好的改进。莫兰散点图将空间划为四个象限,第一象限内的地区属性值高,周围地区属性值也高;第二象限内的地区属性值低,周围地区属性值高;第三象限内的地区属性值低,周围地区属性值也低;第四象限内的地区属性值高,周围地区属性值低。位于第一、三象限的区域属性值与周围地区属性值存在空间正相关,位于第二、四象限的区域属性值与周围地区属性值存在空间负相关。本文运用计量软件Stata空间计量模块绘制各年度省际碳排放强度的莫兰散点图。因本文篇幅限制,仅以表格的形式展现2003年及2015年各省市莫兰指数散点图象限分布,如表2所示:
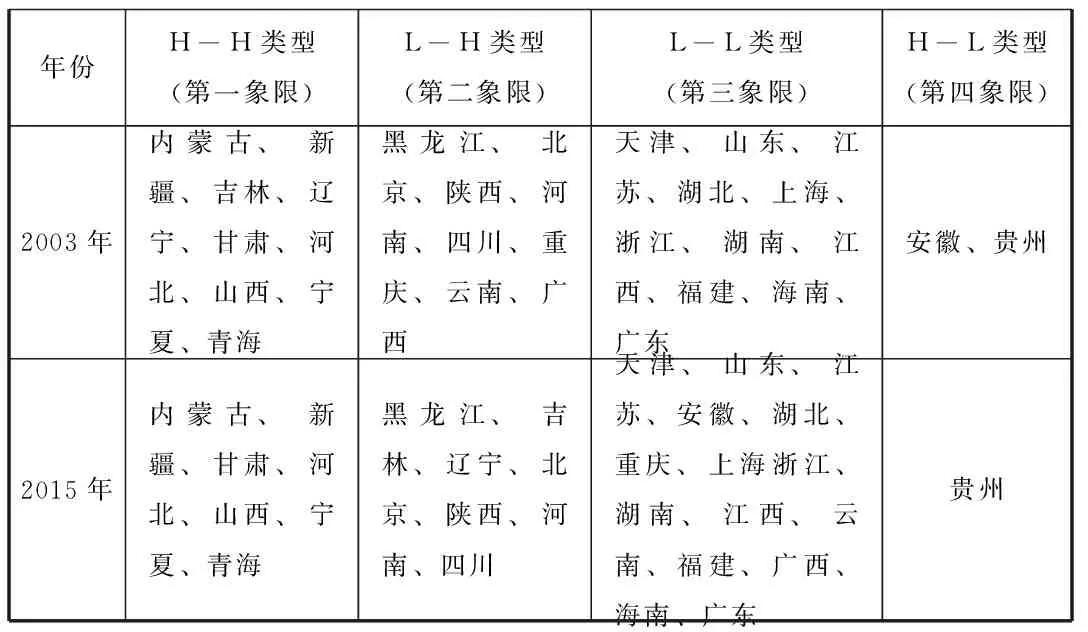
表2 2003年及2015年各省市莫兰指数散点图象限分布
以上分析表明:省际碳排放强度存在空间正相关关系,与传统计量经济理论所假设的不同个体同质且相互独立相背离,因此,在对碳排放强度进行研究时,不能简单的引入传统计量模型,应加入空间效应进行考察,从而表明在相关问题上构建空间计量经济模型的必要性。
四、结论及政策建议
本文通过基于各省市的能源平衡表数据,测算得到我国2003-2015年的碳排放强度数据,并引入了空间权重矩阵,对省际间碳排放强度的相关性进行检验,测算了各年全国范围内的莫尔指数。通过本文的研究,主要得到以下结论:
2003-2015年期间,虽然我国二氧化碳排放量总逐年增加,但大部分省市碳排放强度数据表现为逐年下降,表明节能减排的工作已取得一定成效;从全国角度来看,我国的碳排放总量和碳排放强度都具备“西高东低”、“北高南低”的特征,由于区域内经济发展不平衡和地区差异显著,少部分区域碳排放量和碳排放强度向相反方向演化,表明减排政策的制定需要因地制宜;从省际层面看,针对本文所研究的30个省市中有个别省市碳排放强度水平一直徘徊在高位,且各省际间碳排放强度差异巨大,说明当前不少省市达成碳排放强度下降目标任务艰巨。此外,我国省际碳排放强度存在空间正相关关系而不是相互独立,并且正相关性随着时间表现出逐渐增加的趋势。
基于本文结论,政府应当实施差异化减排策略,重视排放转移问题。正是由于不平衡的发展格局,决定减排策略的制定与实施须因地制宜,不能“一刀切”。应该充分考虑地区发展的不同特点及空间关联效应,尤其是个别区域间的“内涵排放”的问题,以区域为单位,实行连带责任,共同减排的责任分配,而非以单个省市为个体。
【注释】
①由于海南省为独立岛屿不与任何其他省份接壤,为便于分析,在设置空间权重矩阵时将其设置为与广东省相邻。
[1]IPCC国家温室气体清单指南(1996年修订版)
[2]林伯强,黄光晓.梯度发展模式下中国区域碳排放的演化趋势——基于空间分析的视角[J].金融研究,2011,12:35-46.
[3]林光平,龙志和,吴梅.我国地区经济收敛的空间计量实证分析:1978—2002年[J].经济学(季刊),2005,S1:67-82.
[4]孙耀华,仲伟周.中国省际碳排放强度收敛性研究——基于空间面板模型的视角[J].经济管理,2014,12:31-40.
[5]王娟,张克中.中国省域碳排放趋同与经济增长[J].经济管理,2014,06:34-43.
[6]王群伟,周鹏,周德群.我国二氧化碳排放绩效的动态变化、区域差异及影响因素[J].中国工业经济,2010,01:45-54.
[7]王艺明,张佩,蔡昌达.低碳经济下中国碳排放强度收敛性的实证检验[J].厦门大学学报(哲学社会科学版),2014,02:120-128.
[8]许广月.碳排放收敛性:理论假说和中国的经验研究[J].数量经济技术经济研究,2010,09:31-42.
