K-均值聚类与决策树C4.5算法在成绩分析中的应用研究

(重庆工商大学数学与统计学院 重庆 400067)

引言

学生的成绩分析是高校管理中的最重要一环，是进行综合素质测评的依据，但目前各高校采取的是比较简单浅层次的分析，且不重视各科之间和各科与总成绩之间的种种关联，只以总成绩的高低来作为划分成绩等级的依据，忽略了各科目的难易程度、重要程度、教学水平的差异程度等因素。所以，为帮助老师合理地开展和改善教学工作，更好地找到影响成绩的相关因素，制定科学有效的成绩分析模型是非常必要且不可忽视的重中之重。

一、决策树原理及其经典算法

(一)决策树原理

决策树(Decision Tree)是机器学习中最基础且应用最广泛的算法模型，也是最经常使用的数据挖掘算法，是一种有监督的学习方法。具体来讲它是通过一系列规则对数据进行分类的过程，关键步骤在于找到对划分数据分类时起决定性作用的某种特征。它通常的表现形式为附加概率结果的树状结构决策图，以最直观的表示形态来展现结果。决策树的原理和算法相对直观简单，再加上它效率高可反复利用等特点，被越来越多的读者使用。

(二)ID3算法简介

ID3算法是决策树的一种，ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法的缺点在于处理大型数据速度较慢，不可以并行和不可以处理数值型数据，只适用于非增量数据集。它的基本步骤为：(1)计算分类系统信息熵(2)计算条件熵(3)计算信息增益量。

(三)C4.5算法简介

C4.5算法可以看成是ID3算法的后续算法，但它是基于信息增益比的分类决策方法，即其根本区别就在于C4.5算法在选取决断特征时选择信息增益比最大的，即分类决策的依据有些不同，但都是贪心算法的运用，且在递归和结构上大致相同。在C4.5算法的决策树中，每个节点都保存了可以用于计算某值属性的信息。

(四)ID3算法与C4.5算法的比较和选取

在决策树算法中，C4.5算法可以看做是ID3算法的一个后续发展，在分类决策的依据和处理的广泛性问题上均有所优化。其具体优势如下几点：(1)用信息增益率来选择属性：在ID3算法中使用信息增益来选择属性，这无疑会造成会偏向于选择值多的属性。(2)对非离散数据即连续数值型数据也能处理。(3)在决策树的构造过程中对树进行剪枝：这就改进了在ID3算法中树的高度无节制地增长和过度拟合数据的出现。(4)能够对不完整数据也能够进行处理。

综上看来，C4.5算法在算法的效率和性能程度上较优于ID3算法。为选取C4.5算法运用于下文的实例分析，下面具体阐述C4.5算法的实际计算步骤：

设训练样本数据集X={X1,X2,…Xn}，属性集Q={Q1,Q2,…Qm}，Qm的值域为{q1,q2,…qt}，则：

第1步：求得不同类别的信息熵为

①

第2步：属性Qm的信息熵为

②

第3步：属性Qm的信息增益为

gain(X,Qm)=M(X)-B(X,Qm)

③

第4步：属性Qm的信息增益率为

ratio(X,Qm)=gain(X,Qm)/split(X,Qm)

④

其中对属性Qm的分割信息量定义为

数据集对Qm的条件熵为

M(X,Qm=qj)=∑(-P(Xi|Qm=qj)log2P(Xi|Qm=qj)

二、K-Means聚类算法

K均值聚类算法属于聚类分析方法中一种较为基本的且应用广泛的划分方法，是一种无监督的学习算法，它将相似的数据归纳到同一簇中，即在无类标号数据中发现簇和簇中心的方法，在SPSS中即可完成。首先算法以K个初始点作为质心，然后将N个数据对象划分为K个聚类，最后再根据距离中心点的最短距离不断调整质心，利用各聚类中对象的均值所获得的一个中心对象来计算并定义“相似度”。此算法要求满足，分类对象在同一聚类中的相似度较高，而在不同聚类中的相似度较低。整个流程图如下图1所示：

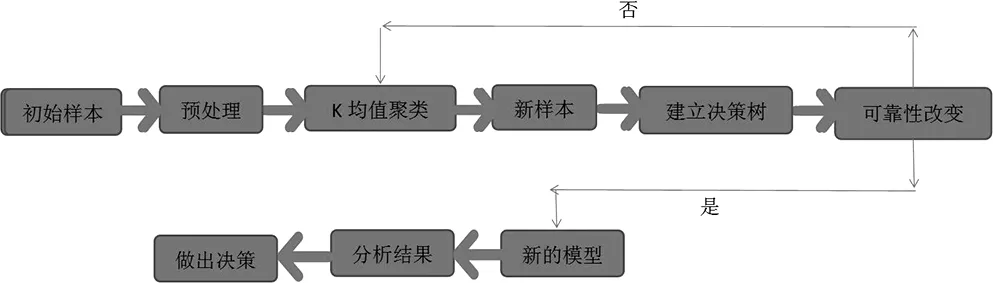
图1 模型流程图

三、基于K均值聚类和决策树C4.5算法的实例分析

(一)数据的预处理与聚类

本文选取的数据样本来源于某高校大三年级统计学专业学生的期末考试成绩。在原始数据中，个别学生有缺考、休学等情况，在进行聚类分析和决策树的构造之前可以将此类数据看成无效数据给予清除，此例中无效数据只有2个，最终可处理的样本数为48个，预处理后得到表1：

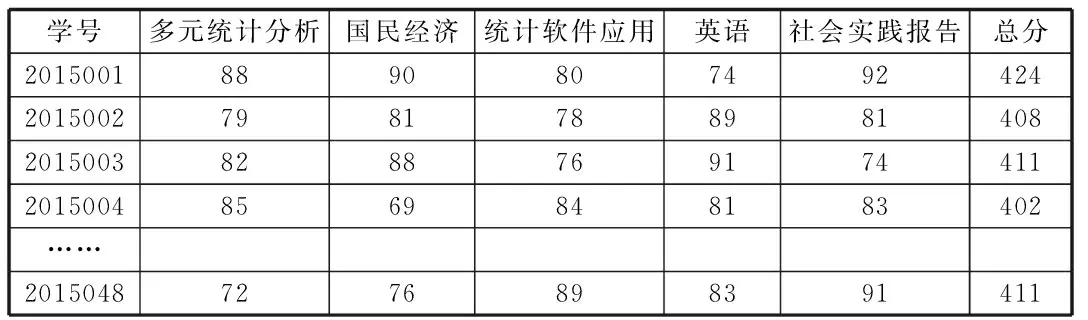
表1 大三上统计学专业(1)班期末成绩

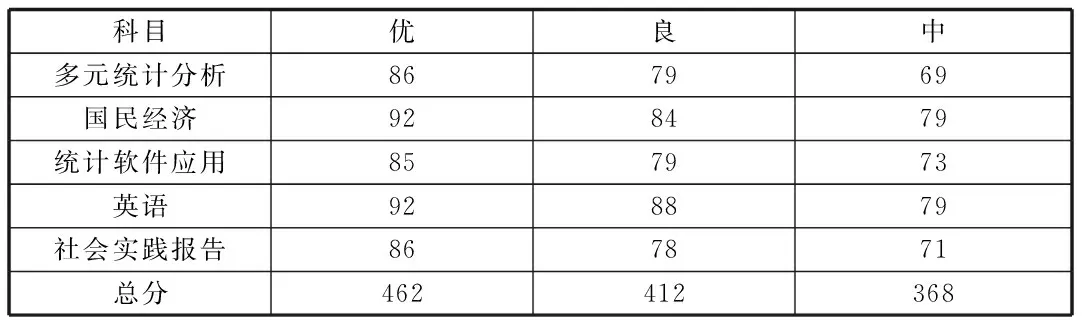
表2 各等级的聚类中心点(分)

首先运用SPSS将进行K-均值聚类，将期末成绩分为“优、良、中”三个等级。聚类后的结果包括各等级的聚类中心和各等级相对应的人数，分别见表2、表3。由于篇幅问题，这里仅将“多元统计分析“这个科目与总成绩的等级人数细分情况给予展示，具体见表4：

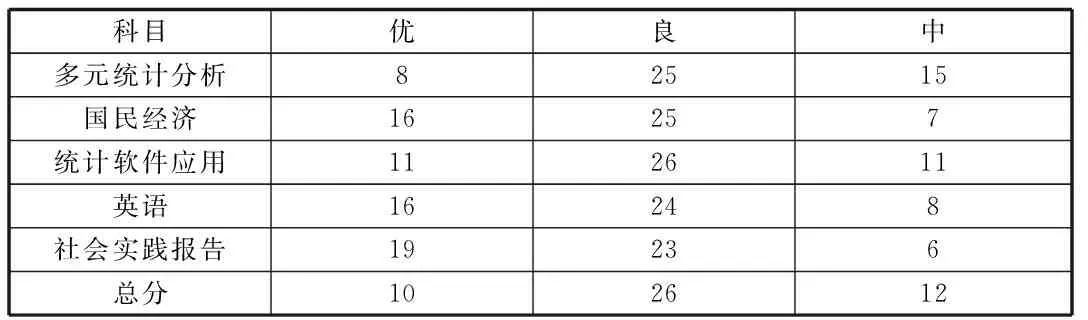
表3 各等级的人数(人)

表4 多元统计分析成绩与总成绩等级对应人数

通过K均值聚类后就可以更加清楚直观地看到，各个科目成绩的重心点、各科成绩在三种等级下的人数分配、总成绩在三种等级下的人数分配，对这个班学生成绩水平的大致情况有了个直观了解。

(二)决策树的构建

首先，根据表3中总分在各等级下的人数情况，根据公式(可算得不同类别的信息熵为：

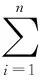
然后，针对“多元统计分析”进行信息熵。

如表4所示，在此成绩为“优”的情况下，其中总成绩为“优”的有6人，总成绩为“良”的有2人，总成绩为“中”的有0人。根据公式(可得该科目成绩在等级为“优”的情况下的子集信息熵：

B(X,Qm)1=-6/8*log2(6/8)-2/8*log2(2/8)

同理，该科目成绩在等级为“良”的情况下的子集信息熵：

B(X,Qm)2=-9/25*log2(9/25)-12/25*log2(12/25)-4/25*log2(4/25)

该科目成绩在等级为“中”的情况下的子集信息熵：

B(X,Qm)3=-3/15*log2(3/15)-9/15*log2(9/15)-3/15*log2(3/15)

其次，根据公式(和44求得“多元统计分析”的信息熵和信息增益率。

gain(X,Qm)=8/48*B(X,Qm)1+25/48*B(X,Qm)2+15/48*B(X,Qm)3

ratio(X,Qm)1=gain(X,Qm)/split(X,Qm)=gain(X,Qm)/-8/48*log2(8/48)-25/48*log2(25/48)-15/48*log2(15/48)=0.444

同理可求出“国民经济、统计软件应用、英语、社会实践报告”的信息熵和信息增益率，由于篇幅问题这里就不一一列出，直接列出其余课程的信息增益率：

ratio(X,Qm)2=0.376ratio(X,Qm)3=0.402ratio(X,Qm)4=0.362ratio(X,Qm)5=0.195

由此可见，“多元统计分析”的信息增益率最大，可选作首个节点以C4.5算法分裂其“优、良、中”3个属性。

(三)规则提取和规则结果分析

总评为“优”的规则提取如下：1.若“多元统计分析”成绩为“优”且“统计软件应用”成绩为“优”，则可直接判定为“优”。2.若“多元统计分析”成绩为“良”且“统计软件应用”、“英语”、“国民经济”成绩均为“优”，则可判定为“优”。

总评为“中”的规则提取如下：若“多元统计分析”成绩为“中”且“国民经济”成绩为“良”或“中”。相对于那些学位公共课，“国民经济”课程相对较通俗易懂，取得高分的几率应该在所有学科中比较大；若像“多元统计分析”这样的必须掌握的学位专业课为“中”，且“国民经济”这样的公共课为“良”或“中”，这着实反应出该类学生对必须掌握的课程以及最简单的课程都没有好的成绩，从一定程度上可以说明该学生的学习态度不太端正，才会导致总体情况不容乐观。其余具体情况见下图2所示(为简明书写，各学科以最前面的两个字表示)：

图2 决策树规则展示

由上分析可知，单凭总成绩的高低来分析成绩是不太科学合理的，其中的“多元统计分析”和“统计软件应用”为统计学专业学生的学位专业课，学生想要学习好专业技能以便更好地找工作，那么学好这两门课是必要的。当然，这两门学科的学科难度是相对较大的，能在期末考试中取得高分的同学在一定程度上可以说明是比较优秀的。在今后的教学中，对此类学科的教学管理方法也应该加以重视。一般来讲，专业课成绩比较好的其他课程成绩也相对较不错，而连学位公共课成绩都不太好的学生其他成绩也更是不容乐观，这一点也符合常理。

四、结论

由于K均值聚类法的“算法简单快速，具有较高的效率且可收缩”等优点，首先选取了此类无监督的学习算法将数据进行合理地分类。再考虑到目前比较流行的决策树算法易于理解较为直观，对ID3和C4.5算法综合比较，优选出基于C4.5算法的决策树来进行规制的构造。通过对实例“学生期末考试成绩的评定”的分析，摒弃了原始的按总分成绩来划分等级的不合理规制，将K均值聚类法和决策树的C4.5算法引入其中，得出了全新的成绩评定规则，从分析的过程和结果上看，此类算法更加科学合理。

[1]饶秀琪，张国基.基于KPCA的决策树的方法及其应用[J].计算机工程与设计，2007

[2]葛宏伟，杨镜非.决策树在短期电气负荷预测中的应用.[J].华中电力，2009

[3]Han Jiawei,Kamber M.数据挖掘：概念与技术[M].北京:机械工业出版社，2005

[4]姚双良.数据挖掘在高校课程相关性中的应用研究[J].科技通报，2012

[5]高阳，廖家平，吴伟.基于决策树的ID3算法与C4.5算法[J].湖北工业大学学报，2011

[6]哈申花，张春生.基于C4.5决策树学生成绩数据挖掘方法[J].内蒙古民族大学学报，2010