丝绸之路下枢纽港口的选择研究

(北京工商大学 北京 100048)

引言

国际经济形势复杂，欧美等国动辄以反倾销及提高进口标准为手段打压中国的海外贸易，要想实现更为公平的贸易往来，必须主导开辟一条新的贸易之路，国家领导人提出了“一带一路”经贸发展的长期战略构想。随着亚投行的设立，中国为推动“一带一路”的发展又更进一步。而东起中国，西至欧洲的复杂而庞大的港口网络中，核心枢纽港的选择对整个网络极其重要。中国作为海上丝绸之路的总设计师，必须要从全局的、长期的视角去考量枢纽港的选取及其的重点建设对象。

复杂网络理论中最基本的三个统计量分别是度分布、簇系数和平均路径长度[1]。21世纪初期Watts和Strogatz[2]首先在“小世界网络的集体动力学”一文中定义了复杂网络具有小世界的特性，Albert和Barabasi[3]提出了网络的无标度性质，并且通过模型验证了其产生的合理性。陈国强，陈亮[4]指出中心度值的重要性，并得出了无标度网络中度很高的节点在集装箱海运网络中有很大影响的结论；LI ZHEN FU[5]等研究了班轮航线网络的中心性布局演化规律。Fremont基于马士基公司的班轮数据，构建海运网络结构，并对港口网络结构及港口情况进行了详尽的分析[6]。

综上，目前针对复杂网络枢纽港口的研究主要基于中心性布局和最短路下的最小成本，中心性布局如度分布，这种衡量指标在很大程度上反映了中心枢纽的连通性，对于中心港口的选取具有很大的参考意义。其不足之处在于只注重定性分析而忽略了网络运行最小成本这一重要参考指标，而基于最小成本的Floyd算法，可以弥补基于中心性布局的缺陷。然而若单纯易最短路求解，一方面运算量巨大，另一方面也忽略了中心性布局所带来的辐射及隐形效益，因此，本文尝试结合两种算法求解枢纽港口的布局问题。

一、基于度分布的枢纽港的初选

(一)度分布

度分布又称连通度，节点i的度k(i)是指与该节点相连接的边的数目，度分布是网络的一个重要统计特征，它主要衡量整个网络的连通性。度值计算公式如下(1)

(1)

其中n是网络中的总的节点数，当i与j之间有边相连接是xij=1，否则，xij=0。网络中节点i的度分布也可以用分布函数p(k)表示，它指任意节点i的度为k的概率。

(二)网络分布及度值求解

海上丝绸之路东洋航线由中国沿海港口至朝鲜、自本；西洋航线由中国沿海港口至南亚、阿拉伯和东非直至西欧沿海各国；南洋航线由中国沿海港口至东南亚各国。曾庆成[7]在《21世界海上丝绸之路港口发展报告》一书中，通过分析全球十大班轮公司的靠港数据，引入了由82个干线港口构成的海上丝绸之路航线网路。本文在此为基础上进行合并添加，由于东洋航线干线港口规模以及竞争结构相对稳定，并且海上丝绸之路的侧重点在于建设西洋和南洋航线，所以本文未将东洋航线港口包括在内，仅添加西洋航线的代表性港口。

二、基于Floyd最短路算法优化基于度值的枢纽港选择结果

(一)数据选择与处理

现有枢纽港口已经被广泛认可，至少在局部地区其规模效应非常明显，然而将其放进海上丝绸之路复杂网络的全局中，其是否为最佳选择还未进行验证。由于单纯用基于度值的枢纽港口既具有缺陷又具有一定的合理性，本章借鉴其合理性的部分—度值较大的节点与中心点的高度相关性，选出度值排名前15的港口，在其基础上利用最短路算法，从最小成本的角度确定枢纽港口。

(二)模型及算法

1.基本假设

假设1：港口运输成本与距离成正比，以港口之间的距离作为一个流量单位的成本。

假设2：每对(i,j)流最多经过枢纽港中转两次，各港口不限制流量。

假设3：根据中枢辐射航线网络设计要求，枢纽港口之间完全连接,非枢纽港口之间不能直接连接,非枢纽港口之间的客流必须通过枢纽港口进行中转运输。

2.基于距离与成本成正比的假设下建立模型

(2)

(3)

(4)

(5)

(6)

yk∈{0,1},k=1,…,n;xiuvj≥0;i,j,k,m=1,…,n

(7)

目标函数(2)表示最小成本；约束条件(3)表示枢纽港个数为q；约束条件(4)表示所有的(i,j)流都必须从起点港口运送到目的地港口；约束条件(5)(6)表示所有的(i,j)流都必须经过枢纽港口中转；约束条件(7)为非负性约束。

3.Floyd最短路算法

假定枢纽集R=r1,r2…rp，构造图G=(N,E)。定义G中所有边的长度lij为：

当i,j∉R时，lij=+∞；当i,j∈R时，lij=αcij；当i∈R,j∉R时，lij=δcij；当i∉R,j∈R时；lij=γcij。

(2)对于任意1≤i≤n,1≤j≤n,令

(3)如果u=p，结束；否则，令u=u+1，重复(2)；

(四)算例分析

港口度值的大小反映了该港口作为枢纽港口的连通性，若选择度值较小的港口作为备选枢纽港就会失去度值中心性。所以本文收集了2016年度值排名前15的港口集装箱吞吐量，对其处理如下：当i确定时，Lij与j的度值成正比，则2016年15个港口之间的集装箱吞吐量如表2所示(单位：TEU)。

表2 15港口集装箱吞吐量(单位:十万TEU)

假设p=3，α取值不定时，其最优化结果如表2-3所示。

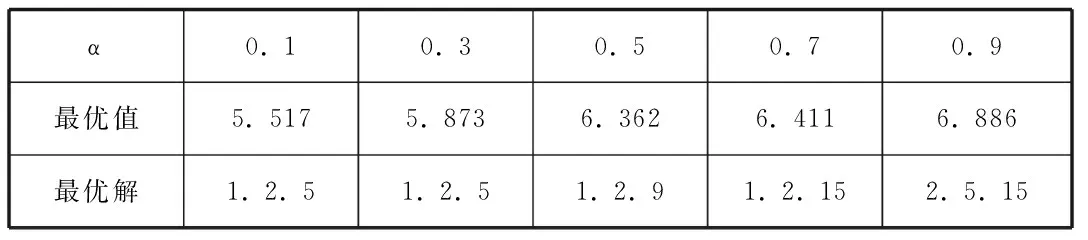
表2-3 p=3，α取值不定时，其最优结果(单位：千亿)

由上述结果可知，当取不同的α值时，最优解的值不尽相同，其中上海港在不同的取值下均为最优解，其次为新加坡港、巴生港、迪拜港和孟买港。而单纯以度值中心性为指标选取的枢纽港口为新加坡、上海、宁波港，两个结果相比虽然前两位相同，但是第三个完全不同，而且当确定p=3时，根据不同国家政治、腹地经济等考虑后确定的α值不同，其差异会进一步放大，因此优化后的结果有三个实践价值：(1)决策结果兼顾连通性和全网络成本最小性；(2)由于枢纽港口的折扣因子取值取决于政治经济等因素的影响，为决策者提供不同折扣因子下α的枢纽港口的选择；(3)即使在折扣因子α取值确定的条件下，其他港口最优解港口仍有很大的价值，这些港口无论在网络连通性还是在实现网络总体成本最小化上，相比其他沿线港口都有绝对的优势，可以考虑将其打造为副枢纽港口，进一步推动丝路的科学发展。

三、结束语

本文基于度分布计算出海上丝绸之路沿线85个港口度值，在此基础上筛选出度值较高的15个海上丝路沿线港口，由结果可知，各个港口度值均大于15，保证了备选枢纽港口具有较高的连通性。

本文在受外部环境因素影响不能确定α条件下，在备选枢纽港口基础上通过Floyd最短路算法确定海上丝绸之路沿线核心枢纽港口的布局，为海上丝绸之路核心枢纽港口选择提供更多参考。由结果可知：当α取值变化时，最小成本选择下的枢纽港口在不断变化，可以为决策者提供不同情境下的决策参考，同时选择结果兼具连通性和经济性，并提醒决策者要重点关注的非枢纽港口，具有一定的现实参考意义。

[1]郭世泽，陆哲明。复杂网络基础理论[M]。北京:科学出社，2012。

[2]Watts D J,Strogatz S H.Collective dynamics of ‘small world’networks[J].Natnre,1998,393(6684):440-420.

[3]Barabasi A L,Albert R.Emergence of scaling in random networks[J].Science.1999,286(5439):509-512.

[4]陈国强，陈亮。一种基于资源分配策略的复杂网络中心性测度[J]。计算机科学。2011，38(8)：42-44。

[5]Li Zhenfu,Xu Mengqiao,Shi Yanlei,et al.Centrality in global shipping network basing on worldwide shipping areas[J].Geo Journal，2015,388(10):47-60.

[6]王杰，王晓斌。基于K-壳分解的集装箱海运网络度分布研究[J]。武汉理工大学学报，2014，38(1)：25-30。

[7]曾庆成。21世界海上丝绸之路港口发展报告[M]。大连：大连海事大学出版社，2015。