纤维在输纤通道气流场中运动的模拟

林惠婷， 汪 军(1.东华大学 纺织学院， 上海 201620； 2.泉州师范学院 纺织与服装学院, 福建 泉州 362000； 3.东华大学 纺织面料技术教育部重点实验室， 上海 201620)

转杯纱的性能与纤维在输纤通道和转杯内的运动形态有着密切的关系。在转杯纺纱中，经过分梳辊梳理的单纤维是在气流的作用下经由输纤通道转移到凝聚槽中，因此输纤通道内的气流流动特征对纤维的形态有重要的影响。输纤通道几何结构、转杯纺纱工艺参数等通过影响转杯纺纱器通道内的气流流动特征来影响纤维形态，从而影响成纱的结构与性能[1-2]，因此研究气流/纤维两相流问题对于深入了解转杯纺纱技术以及优化成纱工艺参数和纺纱器结构的设计有重要的意义。

随着计算机技术的发展，数值模拟成为研究气流/纤维两相流动的重要手段。数值模型主要分2类:一类是将颗粒相与流体相当成连续相，称为两流体模型；另一类是将颗粒相看成离散相，流体相为连续相，称为连续-离散模型。由于纤维长径比大，且具有弹性和柔性等特征，因此一般采用连续-离散模型来模拟气流/纤维两相流动。

气流/纤维两相流的研究难点是纤维力学模型的建立：Smith等[3]将纤维看成是一系列球杆组成的长链，并考虑了纤维的刚度，模拟了纤维在层流中的加速运动；Bangert等[4]假设纤维为刚性杆，模拟纤维在无旋的低速流中的运动；Yamamoto等[5]建立的纤维模型是由n个半径为a的相互连接的小球组成的长链，改变小球之间的连接距离、连接角度以及扭转角度可模拟纤维的拉伸、弯曲和扭转；Kong等[6-7]提出以分散节点和不计质量的柔性链组成的长链作为纤维模型；Zeng等[8]充分考虑了纤维的柔弹性，建立了由n个珠子和n-1根不计质量的杆组成的长链，并模拟了纤维在喷气纺喷嘴气流场中的二维运动。

本文在建立输纤通道气流场数值模型的基础上，建立纤维在气流场中的动力学方程，以期对纤维在输纤通道内的运动形态进行研究，从而为优化转杯纺纱器的结构设计提供理论依据。

1 输纤通道气流场数值模型建立

1.1 几何模型

数值计算区域为转杯纺纱器内气流流动的空隙区域，包括排杂通道、分梳腔、输纤通道、转杯腔体和引纱通道，如图1所示。在笛卡尔坐标系下建立该几何模型，坐标原点位于转杯杯底中心，y轴为转杯中心轴，其正方向沿着转杯杯底指向杯口，x-z平面与y轴垂直。几何模型的各结构尺寸见图1所示。

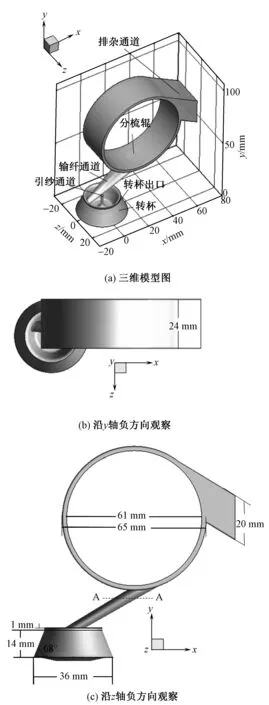
图1 计算区域的三维结构及尺寸Fig.1 3-D model and dimensions of computational region. (a) 3-D model； (b) Observation along -Y direction; (c) Observation along -Z direction

1.2 系统描述

由于转杯纺纱器通道较小，且转杯和分梳辊旋转一周所用的时间非常短暂，可认为气流流动不产生热交换。假定转杯纺纱器内的气流为不可压缩流体，则其所满足的控制方程为

div(ρu)=0

(1)

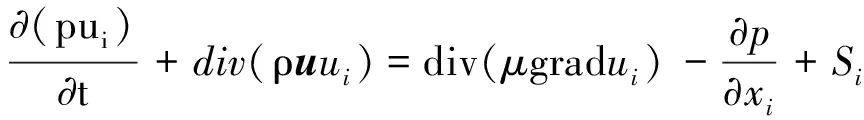
(2)

式中：ρ为气体的密度；u为气流速度矢量；ui(i=1, 2, 3)是u在坐标分量xi(i=1, 2, 3)方向的分量；t为时间；μ为动力学黏度；p为压力；Si为xi方向的广义源项。

流场采用稳态、隐式求解器、RNGk-ε湍流模型及壁面函数法进行计算，对流项采用二阶迎风格式离散，用SIMPLE算法对流场进行求解。

1.3 网格划分和边界条件

采用GAMBIT网格生成软件对计算区域进行网格划分。由于计算区域的形状较为不规则，因此采用分块划分方式。引纱通道采用六面体结构网格，转杯和输纤通道采用四面体非结构网格，并对转杯和输纤通道的近壁区域进行网格细化。

边界条件的设置为：1)进口边界。排杂通道和引纱通道均与外界大气相通，将这2个入口设为压力入口，其静压值为一个标准大气压；2)出口边界。转杯出口设为压力出口；3)固体边界。所有的固体壁面均采用无滑移边界条件。转杯壁面和分梳辊壁面为旋转壁面，转杯角速度向量方向指向y轴，分梳辊角速度向量方向指向z轴。

2 纤维在输纤通道流场中运动的模拟

2.1 纤维模型的建立

纤维被视为由n个球状珠子和n-1根与球状珠子等直径的圆柱杆线性连接而成的长链。在纤维链中，第i个珠子只与第i-1及i+1个珠子相邻，则第1个和第n个珠子分别为头端珠和尾端珠，如图2所示。

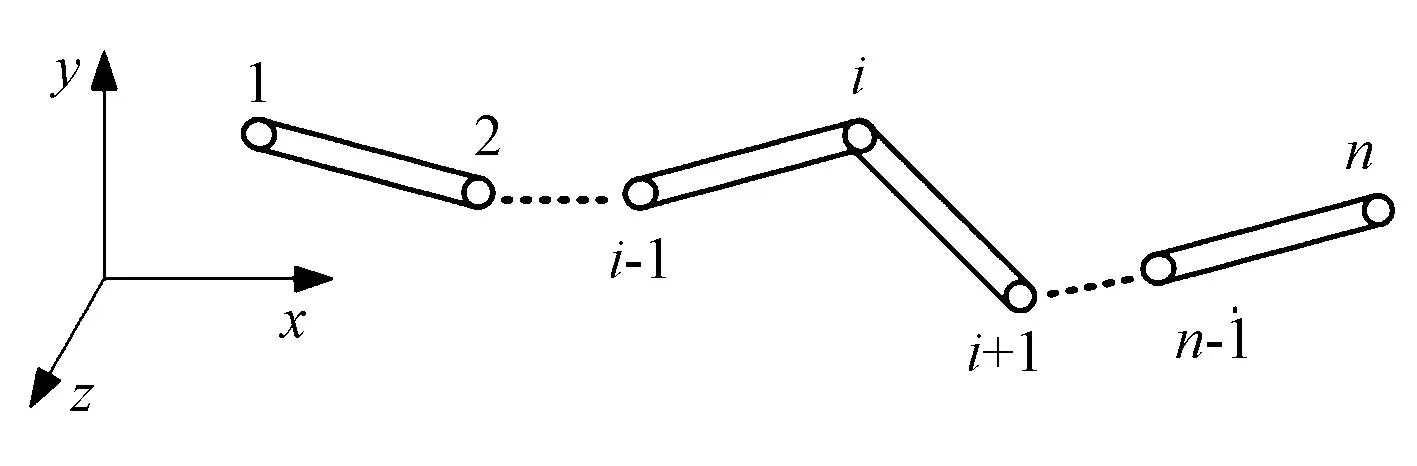
图2 纤维模型示意图Fig.2 Schematic diagram of fiber model

假设纤维的质量和受力只集中在球状珠子上，则珠子在气流场中的空间位置变化即代表纤维随时间变化在气流场中的运动。

珠i的质量mi表示为

mi=Nfli(i=1, 2…,n)

(3)

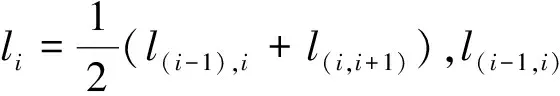
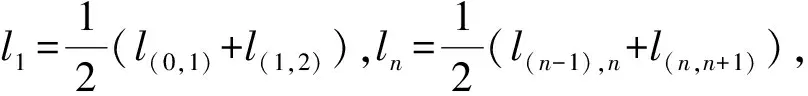
由于纤维在输纤通道气流场中自由运动，纤维受到拉伸、压缩以及绕自身轴线扭转的可能性非常小，因此本文假定纤维受到的拉伸力、压缩力以及扭转力为零。

2.1.1弯曲回复力

若纤维段(i,i+1)与纤维段(i-1,i)产生角度θi时(见图3)，则表示纤维段(i,i+1)受到弯曲力矩Mbi的作用，Mbi定义为

Mbi=-kbθi

(4)

式中kb是与抗弯刚度有关的弯曲常数，为

(5)

式中：E为纤维的弹性模量；Ib为纤维横截面对纤维中心轴线的惯性矩，对于圆形截面有

(6)

式中，df为纤维直径。

θi可通过下式求解得到。

cosθi=eiei+1

(7)

式中：ei和ei+1分别为纤维段(i-1,i)和纤维段(i,i+1)的单位向量。

因此纤维段(i,i+1)受到的弯曲回复力Fbi为：

(8)

Fbi垂直于ei+1并指向平衡位置。

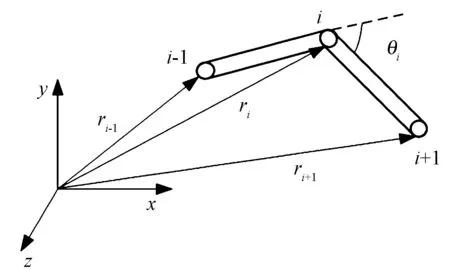
图3 纤维弯曲示意图Fig.3 Schematic diagram of fiber bending

2.1.2流场阻力

纤维在流场中所受外力主要是由流场施加的[9-10]。流场对纤维的作用力主要表现为阻力，同气体特性、纤维形状及其在流场中的取向均有关[11-13]。考虑纤维段(i,i+1)在气流场中受到的阻力可表示为

(9)

式中：Φ和Φ⊥分别称为球形度和横向球形度，可通过下式求得：

(11)

(12)

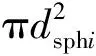
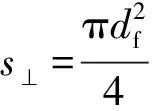
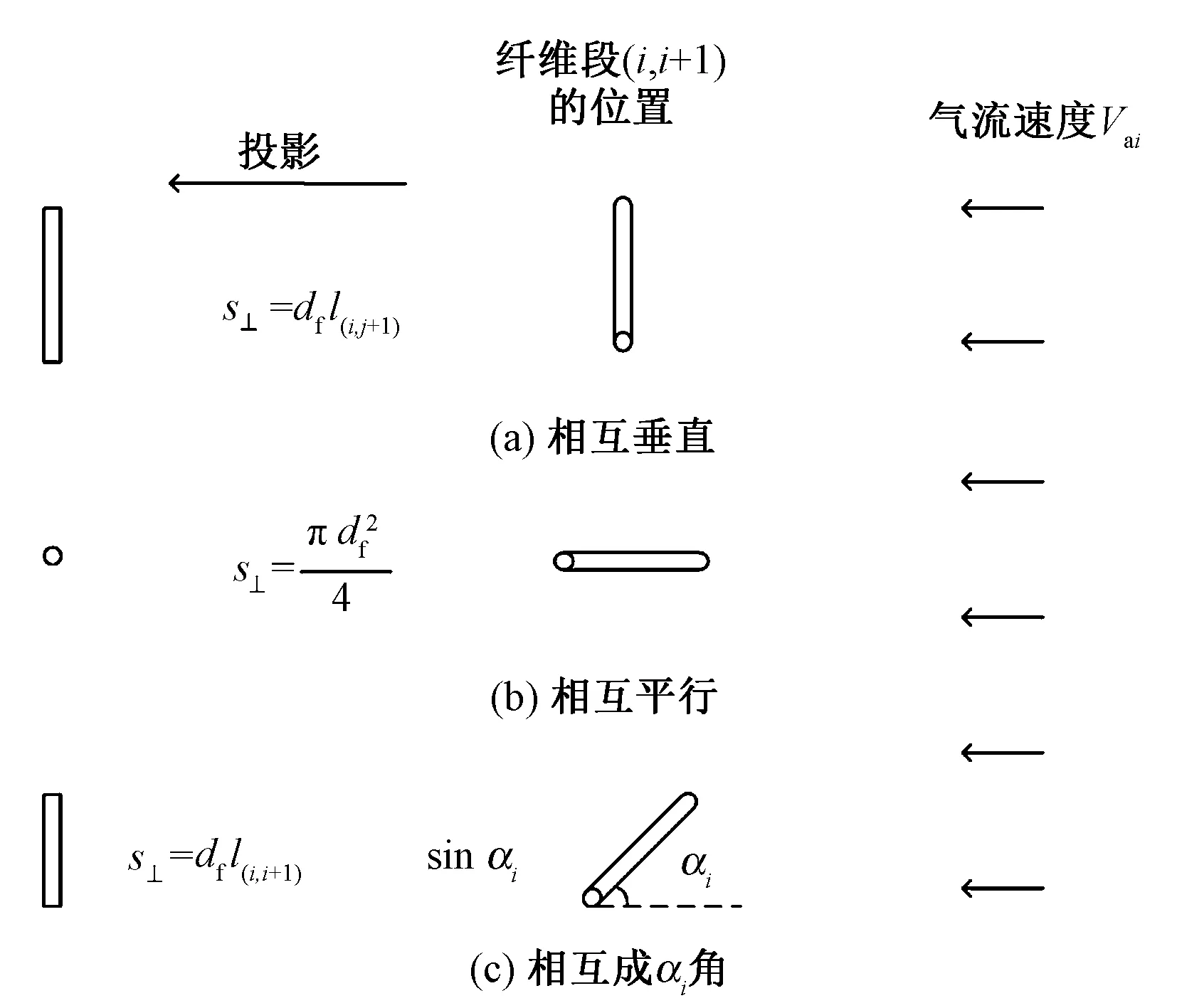
图4 纤维段(i,i+1)与气流速度方向的位置关系Fig.4 Position relationship between fiber section (i,i+1) and air velocity. (a) Vertical position; (b) Parallel position; (c) αi angular

对于纤维段(i,i+1)，雷诺数Re定义为

(13)

式中，μ为空气的动力黏性系数。

2.2 纤维动力学方程

根据牛顿第二定律，珠i在气流场中的动力学方程满足下式：

(14)

式中，ri表示珠i在流场中的位置。通过求解珠子在气流场中的动力学方程，可得到不同时刻珠子在流场中的位置，即纤维在流场中的运动轨迹。

3 计算结果

3.1 输纤通道内气流流动特征

图5示出输纤通道的气流流线图。由图可知，沿分梳腔两侧流动的气流到达输纤通道入口时，受气流本身流动状态和输纤通道几何结构的影响，气流在此处汇合并形成2股漩涡。

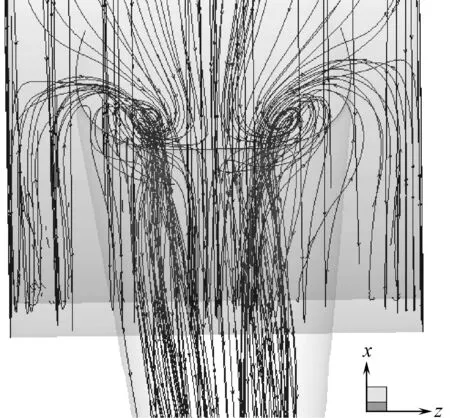
图5 输纤通道气流流线图Fig.5 Airflow streamlines in transfer channel

图6示出输纤通道气流速度分布。

图6 输纤通道气流速度分布Fig.6 Air velocity distribution in transfer channel. (a) Along z axis in Section A-A； (b) Along longitudinal direction

图6(a)示出A-A截面(见图1(c))的气流速沿着z轴方向的分布。图中显示同一个横截面上的气流速度分布不均匀，靠近壁面，气流速度较低(低速区)；中心附近的气流速度较高(高速区)。图 6(b) 示出了气流速度沿输纤通道纵向中心的分布。沿输纤通道纵向中心的气流速度不断增大，该加速气流对单纤维有牵伸作用，其牵伸倍数为输纤通道出口与进口的气流速度之比，这说明输纤通道进出口的速度差异越大，气流的牵伸倍数越高，对纤维的伸直效果越好。

输纤通道的这种气流速度分布对纤维形态的可能影响有：若前弯钩纤维的弯钩部分正好处于高速区，则弯钩会在运动过程中逐渐被消除；若前弯钩纤维的弯钩部分处于低速区，则对弯钩没有太大的改善作用；后弯钩纤维的弯钩部分不管是处于低速区还是高速区，都可能在纵向加速气流的作用下，逐渐得到改善；对于横向纤维(纤维轴向与气流运动方向相互垂直)，其横向的部分在较高速气流的作用下，则逐步运动形成纵向纤维(纤维轴向与气流运动方向相互平行)。

3.2 纤维在输纤通道内的运动

输纤通道内的纤维呈现着各式各样的形态，有近似伸直、对折和弯钩等。弯钩纤维是指纤维的端部与纤维的主体部分有重叠。弯钩纤维受到输纤通道加速气流的牵伸作用，其弯钩部分可能会逐渐伸直[3]。纤维的弯钩程度一般采用弯钩度来表征。弯钩度指弯钩的长度占纤维总长的百分比；弯钩角为弯钩部分轴线与纤维主体部分轴线的夹角[15]。弯钩度越大，表示纤维的弯钩程度越大。

下面重点讨论伸直纤维和前弯钩纤维在输纤通道内的运动形态。由于模拟纤维的三维运动较为复杂，且计算量大，因此本文仅考虑纤维运动的二维模拟。选取中心面x-y(z=-6 mm)作为纤维运动的平面)。

假设纤维直径df=2×10-2mm，纤维线密度Nf=2.0 dtex，拉伸模量E=8 GPa，纤维长度lf=22 mm。纤维从分梳辊脱离之后进入输纤通道，纤维释放位置位于输纤通道入口处：x=0.025 5 mm，y=0.027 5 mm。纤维具有一定的初始速度，假设其初始速度与输纤通道入口处的气流平均速度相同，当纤维头端碰到滑移面时停止计算。

3.2.1伸直纤维

图7示出不同时刻伸直纤维在输纤通道内的空间位置。由于输纤通道的中心截面不存在气流漩涡，伸直纤维在通过输纤通道的过程中依然保持伸直状态。纤维的运动从输纤通道长轴壁面附近逐渐向纵向中心偏移，这与Kong等的研究结果吻合[16]，也可从图6(a)得到解释，即输纤通道纵向中心的气流速度高于壁面处。纤维在输纤通道前半段的运动较为缓慢，而在后半段，随着气流速度加大，纤维运动也逐渐加快。根据纤维头端在输纤通道出口的位置不同，其抵达滑移面时的位置也不相同。值得注意的是，纤维头端接触滑移面的位置不宜过低，这是因为当回转纱条恰好经过输纤通道出口时，纤维易直接搭在回转纱条上形成搭桥纤维，最终形成缠绕纤维。

图7 t时刻伸直纤维在输纤通道内的运动Fig.7 Motion of straight fiber in transfer channel in different time steps

3.2.2前弯钩纤维

弯钩纤维在输纤通道内的伸直情况受到弯钩度的影响。图8示出弯钩度为9.1%、18.2%和27.3%的前弯钩纤维(弯钩角均为60°)在输纤通道内运动的模拟结果。弯钩度为9.1%时，由于弯钩所处位置的气流速度较大，随着纤维向前运动，纤维的弯钩角增大，又由于纤维弯钩度较小，弯钩很快得到消除。弯钩度为18.2%时，弯钩先向前运动，使其形成U状，随着纤维继续向前运动，U状弯钩底部逐渐伸直，弯钩的形状类似于弯钩度为9.1%时的初始形状(即√状)，之后弯钩的伸直过程与弯钩度为9.1%的纤维类似。当进一步增大弯钩度为27.3%时，弯钩的伸直过程与弯钩度为18.2%的纤维类似，即弯钩的中间部分先向前运动，形成U状弯钩，其中间部分再继续向前运动，形成√状弯钩，如此往复，直到弯钩完全被消除。

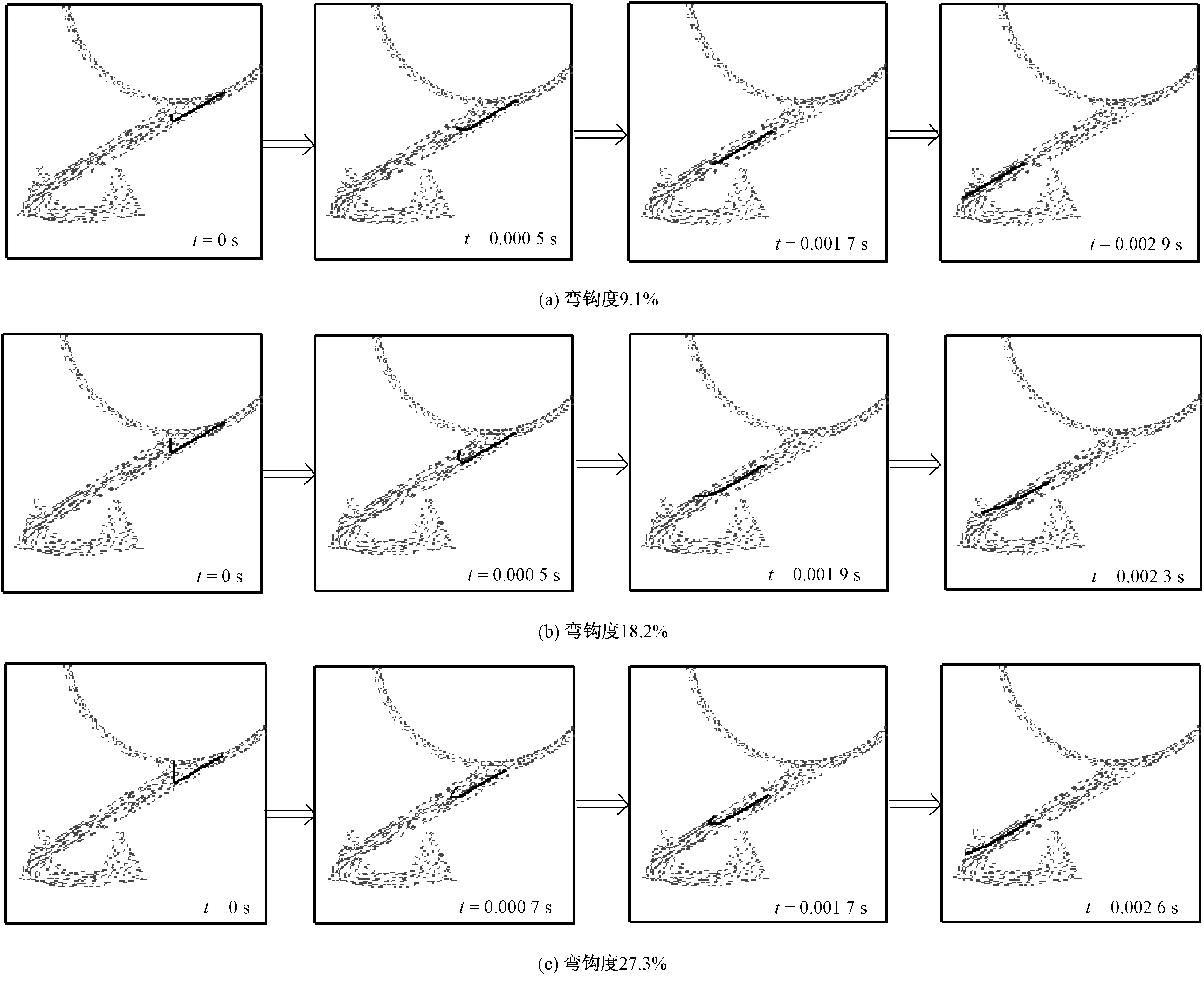
图8 t时刻前弯钩纤维在输纤通道内不同时刻的运动Fig.8 Motion of leading hooked fiber in transfer channel in different time steps. (a) Bending degree of 9.1%; (b) Bending degree of 18.2%; (c) Bending degree of 27.3%

表1示出伸直纤维和弯钩度为9.1%、18.2%和27.3%的前弯钩纤维伸展为直角弯钩角、完全伸直弯钩和头端到达滑移面的耗时。纤维的初始形态对纤维到达滑移面的耗时影响很小，而纤维初始位置则对该耗时有所影响。由表1可知，随着弯钩度增大，纤维伸展为直角弯钩角及弯钩完全伸直的耗时均增大。这是由于纤维的弯钩是逐渐被伸直的，弯钩越长则所需时间越长。随着弯钩度增大，纤维从直角弯钩角到完全伸直的耗时减少，原因在于弯钩度越大，纤维伸展为直角弯钩角的位置越靠近输纤通道后半段，此时通道内气流速度较大，使得进一步伸直弯钩的时间缩短。

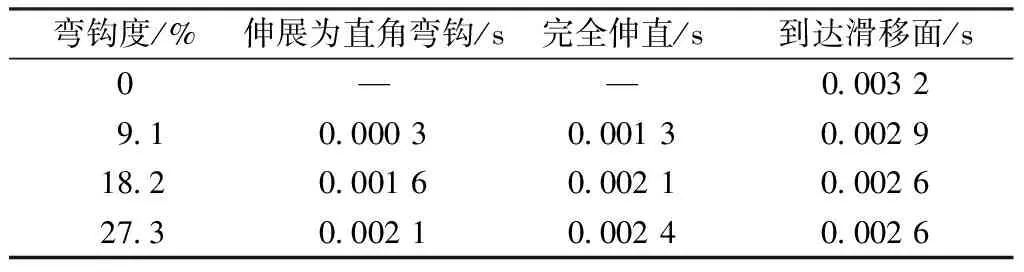
表1 不同弯钩度的纤维达到不同程度的耗时Tab.1 Consuming times of fibers with different bending degrees to be different state

从以上分析可知，输纤通道内的加速气流可伸直弯钩纤维。图6(a)分析了输纤通道横截面的气流速度分布，输纤通道壁面附近的气流速度要比中心的低，若纤维弯钩头端位于壁面附近，而与纤维主体连接的部分处于输纤通道中心，则由于速度差的存在，弯钩容易得到伸直。

需要指出的是，本文所考虑的弯钩纤维的弯钩形态较为理想，实际的弯钩形态要更为复杂，纤维在输纤通道内的伸展情况也会更加复杂。

4 结 论

本文首先采用RNGk-ε湍流模型对转杯纺纱通道气流场进行数值模拟，并在此基础上建立纤维在气流场中的运动方程，从而获得纤维在气流中运动的形态，并分析伸直纤维和前弯钩纤维在输纤通道气流场中运动形态的变化规律，得到以下结论。

1)受气流本身流动状态和输纤通道几何结构的影响，气流在输纤通道入口处形成漩涡；在输纤通道的同一个横截面上，气流速度分布不均匀，通道中心处的气流速度要高于壁面附近；而在输纤通道纵向方向上，气流速度则不断增大。

2)由于输纤通道中心处气流速度较大，纤维倾向于沿着通道中心运动；伸直纤维在输纤通道内容易保持伸直状态，而弯钩纤维则在加速气流作用下逐渐伸直；弯钩度越大，伸直弯钩的耗时越大。

FZXB

[1] 张礼会, 张百祥. 转杯纺纤维输送管道的研究 [J]. 中国纺织大学学报, 1991, 17(6): 16-24.

ZHANG Lihui, ZHANG Baixiang. A study of fiber transfer channel in rotor spinning [J]. Journal of China Textile University, 1991, 17(6):16-24.

[2] LIN H T, ZENG Y C, WANG J. Computational simulation of air flow in the rotor spinning unit [J]. Textile Research Journal, 2015, 86(2): 115-126.

[3] SMITH A C, ROBERTS W W. Straightening of crimped and hooked fibers in converging transport ducts: computational modeling [J]. Textile Research Journal, 1994, 64(6): 335-344.

[4] BANGERT L H, SAGDEO P M. On fiber alignment using fluid-dynamic forces [J]. Textile Research Journal, 1977, 47(12): 773-780.

[5] YAMAMOTO S, MATSUOKA T. A method for dynamic simulation of rigid and flexible fibers in a flow field [J]. Journal of Chemical Physics, 1993, 98(1): 644-650.

[6] KONG L X, PLATFOOT R A. Computational two-phase air/fiber flow within transfer channels of rotor spinning machines [J]. Textile Research Journal, 1997, 67(4): 269-278.

[7] KONG L X, PLATFOOT R A. Fibre transportation in confined channel with recirculations [J]. Computers & Structures, 2000, 78(1): 237-45.

[8] ZENG Y C, YANG J P, YU C W. Mixed Euler-Lagrange approach to modeling fiber motion in high speed air flow [J]. Applied Mathematical Modelling,2005, 29(3): 253-261.

[9] 吴望一. 流体力学 [M]. 北京: 北京大学出版社, 1982: 12-36.

WU Wanyi. Fluid Dynamics [M]. Beijing: Peking University Press,1982: 12-36.

[10] 朱泽飞，林建忠. 纤维状粒子悬浮流动力学分析 [M]. 上海: 中国纺织大学出版社, 2000: 42-66.

ZHU Zefei, LIN Jianzhong. Analysis of Fibrous Particle Suspension Flow Mechanics [M]. Shanghai: China Textile University Press, 2000: 42-66.

[11] GANSER G H. A rational approach to drag prediction of spherical and nonspherical particles [J]. Powder Technology, 1993, 77: 143-152.

[12] LEITH D. Drag on nonspherical objects [J]. Aerosol Science and Technology, 1987, 6(2): 153-161.

[13] HAIDER A, LEVENSPIEL O. Drag coefficient and terminal velocity of spherical and nonspherical particles [J]. Powder Technology, 1989, 58: 63-70.

[14] HOLZER A, SOMMERFELD M. New simple correlation formula for the drag coefficient of non-spherical particles [J]. Powder Technology, 2008, 184(3): 361-365.

[15] 张亚秋. 基于图像处理技术的弯钩纤维表征研究 [D]. 上海：东华大学, 2014: 46-47.

ZHANG Yaqin. The characterization study of hooked fiber based on image processing [D]. Shanghai: Donghua University, 2014: 46-47.

[16] KONG L X, PLATFOOT R A. Two-dimensional simulation of air flow in the transfer channel of open-end rotor spinning machines [J]. Textile Research Journal, 1996, 66(10): 641-650.