基于比例降阶准谐振的MMC环流抑制策略

刘永强, 江 伟,王渝红，陈金祥，黄道姗，龚 鸿，王柯岩

(1.四川大学电气信息学院，四川成都 610065；2. 国网福建省电力有限公司电力科学研究院，福建福州 350007)

0 引 言

模块化多电平直流输电技术(modular multilevel converter, MMC)自2003年首次提出以来，便在直流输电领域引起了广泛的关注和研究[1-2]。模块化多电平换流器为功率单元级联结构,这样有利于实现模块化换流器的冗余设计。模块化多电平换流器具有众多优点，例如，没有换相失败的风险，可向无源网络供电，可以独立控制有功和无功功率，谐波含量少等。但由于模块化多电平自身的结构特点，子模块电容在正常运行时存在较大的电容电压波动，这就导致稳态运行时各桥臂电压不完全相等，因此各桥臂电流中存在一定量的环流。该环流虽然只在换流器三相桥臂之间流动，并不影响交直流侧电流电压，但会导致换流器功率损耗增加，威胁换流器的正常运行，因此必须对其施加抑制。

文献[3-4]利用模块化多电平换流器数学模型及其内部能量关系详细分析了其内部环流产生机理，并指出其为2倍基波频率，且为负序，为环流抑制提供了理论依据；文献[5]基于文献[3]的分析，提出了利用二倍频负序坐标变换和相间解耦的方法，将三相环流分解为两个直流量，但使得的延时增大，也增加了系统的计算量；文献[6-8]提出了一种基于准比例谐振控制的环流抑制策略,但增加了控制器的计算量，占用了内存空间；文献[9-11]采用了重复控制的方法，在离散域内对多次谐波进行无静差跟踪抑制，但其结构较为复杂，在实际应用中存在一些困难；文献[12]采用了PI结合谐振控制的方法，提高了传统比例谐振控制器的响应速度，但这种新的结构同样使得控制器变得更为复杂，难以实现。

本文提出了一种基于比例降阶准谐振的MMC环流抑制器，首先采用二阶广义积分器(second-order generalized integrator, SOGI)取并检测环流中的负序二倍频分量，然后利用比例降阶准谐振控制器(proportional reduced-order quasi-resonant, P-ROQR)对此分量进行无静差跟踪，得到补偿电压，将此补偿电压与原参考波做差，以修正参考波，来减少桥臂间电压的不平衡量，以此达到抑制模块化多电平换流器环流的目的。

1 模块化多电平换流器环流分析

1.1 模块化多电平换流器结构

图1所示为模块化多电平结构图(n+1电平)，其中Ls为网侧等效电感，Rs为网侧等效内阻。模块化多电平换流器共包含三相6个桥臂(每相桥臂分为上桥臂和下桥臂)，每个桥臂包含n个功率单元(submodule, SM)和一个桥臂电感L0。其中桥臂电感用来限制相间环流、减小模块化多电平换流器故障时电流的上升速度，但L0对环流的抑制效果有限。桥臂损耗由桥臂等效电阻R0代替。isx为交流侧电流(x=a,b,c，下同)；usx为MMC交流侧输出相电压；ipx、inx分表表示上下桥臂电流；Udc、Idc分别表示直流侧电压和电流。

模块化多电平换流器的功率单元大致有3种结构：半桥子模块，全桥子模块和箝位双子模块。本文主要研究半桥子模块。每个子模块由2个带反并联二极管的绝缘栅双极型晶体管和1个直流储能电容构成。通过控制每个子模块中的绝缘栅双极型晶体管T1、T2的开通和关断，可以使每个子模块输出Uc和0两个电平。

1.2 环流分析

MMC单相等效电路如图2所示。其中，ip、in分别表示上下桥臂电流；idiff为相间环流；u0、is为模块化多电平换流器出口电压和出口电流。

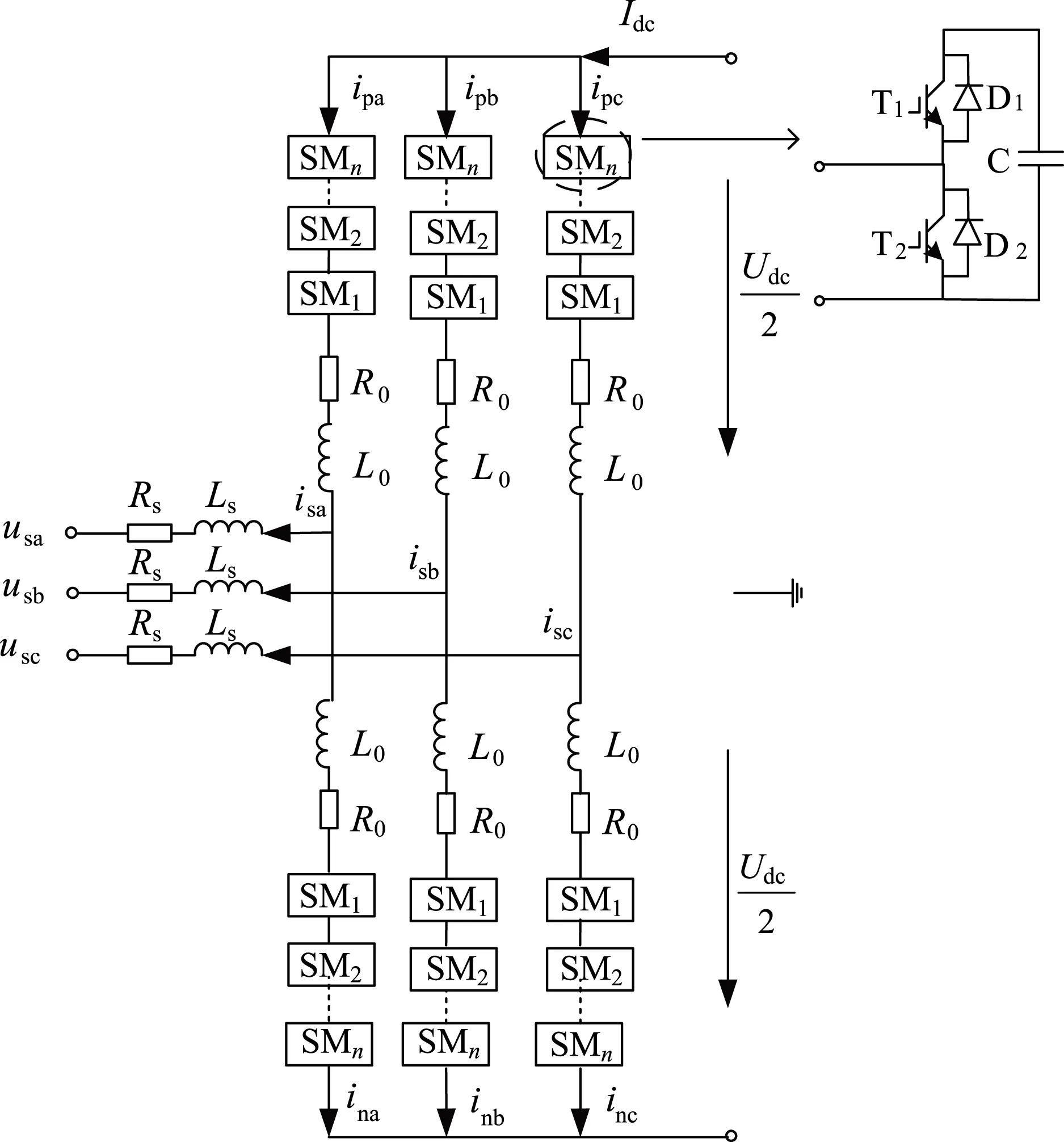
图1 MMC及子模块拓扑结构

图2 MMC单相等效电路图

由于上下桥臂严格对称，由基尔霍夫电流定律有

ip=idiff+is/2

(1)

in=idiff-is/2

(2)

将式(1)和(2)相加有

(3)

由文献[13]分析表明，环流只包含偶数次谐波，其中2次谐波含量最大，且呈负序性质。

因此本文主要以抑制环流中的2次谐波为主。故忽略二次以上高次谐波，只保留二次谐波，则环流表达式可写为

idiff=Idc+I2fcos(2ωt+θ)

(4)

式中：Idc为直流电流；I2f为二倍频环流峰值;θ1为二倍频环流初相角。

在单相系统中，换流器中的直流分量即为直流电流值；而在三相系统中，该分量为直流电流的三分之一。二倍频电流大小则与电容充放电状态有关。直流分量起功率传输的作用，环流分量主要在换流器内部流动，对外部输出电流不会造成影响。但环流会使桥臂电流发生畸变，这样会增加环流器损耗，严重时会威胁换流器的安全稳定运行。

将式(1)和(2)相减有

is=ip-in

(5)

由基尔霍夫电压定律有

(6)

(7)

对于交流侧有

(8)

将式(8)代入到式(6)、(7)并相减得到

(9)

由上式可以看出，输出电流由(up-un)/2决定，因此定义一个内部电动势e。

(10)

将式(6)、(7)相加得到

(11)

由上式可以看出，由于电容电压波动导致的桥臂电压不平衡引起了MMC相间环流的产生。令udiff为桥臂不平衡电压，有

(12)

该不平衡电压是由环流流过桥臂阻抗所产生的压降。

为使得三相桥臂电压保持平衡，减小环流对换流器的影响，需要对相间环流进行抑制。

考虑桥臂不平衡压降及内部电动势有

(13)

(14)

2 环流提取及抑制方法

2.1 二阶广义积分器

本文采用文献[14]所采用的二阶广义积分器(SOGI)来提取并检测该二倍频环流。SOGI结构框图如图3所示，图中虚线框中为SOGI结构。

图3 SOGI结构框图

由图3可以得到整个SOGI的传递函数

(15)

式中：ω0为谐振频率，本文ω0=2πf。

2.2 降阶准谐振控制器设计

传统的环流抑制采用谐振控制器，其传递函数如下:

(16)

该控制器存在两个正负两个共轭的谐振极点，但对于环流抑制来说，只须提取负序二倍频分量，故可对该二阶控制器做降阶处理，只保留需要的谐振点。

对式(16)进行降阶得到降阶谐振函数(reduced order resonant，ROR)如下

(17)

该函数只有一个谐振点。其幅频特性和相频特性如图4。从图中可以看出，该函数在谐振点处具有无穷大增益，且相移180°。同时，可以看出该谐振控制器对谐振点以外的其他频率点的增益急剧衰减，这样即可实现对指定频率的无静差跟踪。

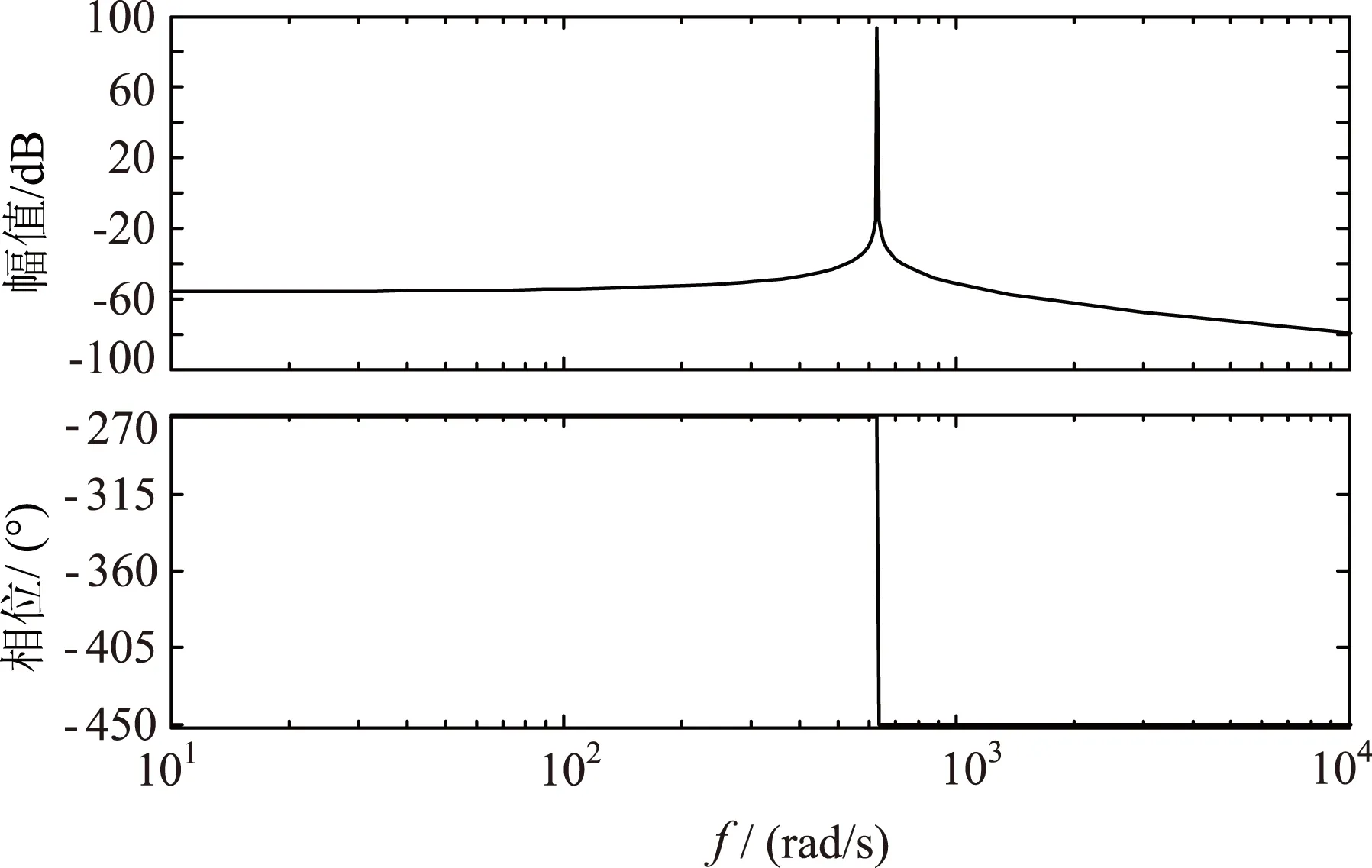
图4 降阶谐振函数伯德图

但ROR的缺点同样明显，即在非谐振频率处的增益过小，当电网频率产生偏移时，控制器无法有效跟踪特定谐波。考虑实际系统频率偏移允许范围为47.5～51.5 Hz。因此，利用增加控制器响应带宽，即采用降阶准谐振器(reduced order quasi-resonant, ROQR)来增加控制器的频率响应范围。降阶准谐振传递函数如下

(18)

式中：ωc为截止频率，一般情况下取5～15 rad/s。

图5为降阶准谐振调节器的幅频特性和相频特性伯德图。取ki=1。

图5 降阶准谐振函数伯德图

从图5可以看出，降阶准谐振的带宽响应范围更广，对实际电网在频率变化的情况下具有更强的适应性。

为提高控制器的响应速度，本文采用比例降阶准谐振控制器传递函数为

(19)

该比例降阶准谐振控制器(P-ROQR)，为一阶谐振函数，实现更为简单，且能快速精确地从谐波中分离得到需要的分量。

由于本文所提出的比例降阶准谐振控制器中存在复数j，控制器的直接实现存在一定的困难。而根据复变函数理论可以知道，复数j表示幅值不变，相位顺时针方向旋转90°。借助两相静止坐标系αβ下两相幅值相等且垂直的特性，即|mα|=|mβ|，∠mα=∠mβ+90°，则有

(20)

故其控制器逻辑框图如图6所示。

结合式(13)、(14)及(18)得出本文所用环流抑制总体框图，如图7所示。

图中所采用的NLM为传统最近电平逼近调制方式。

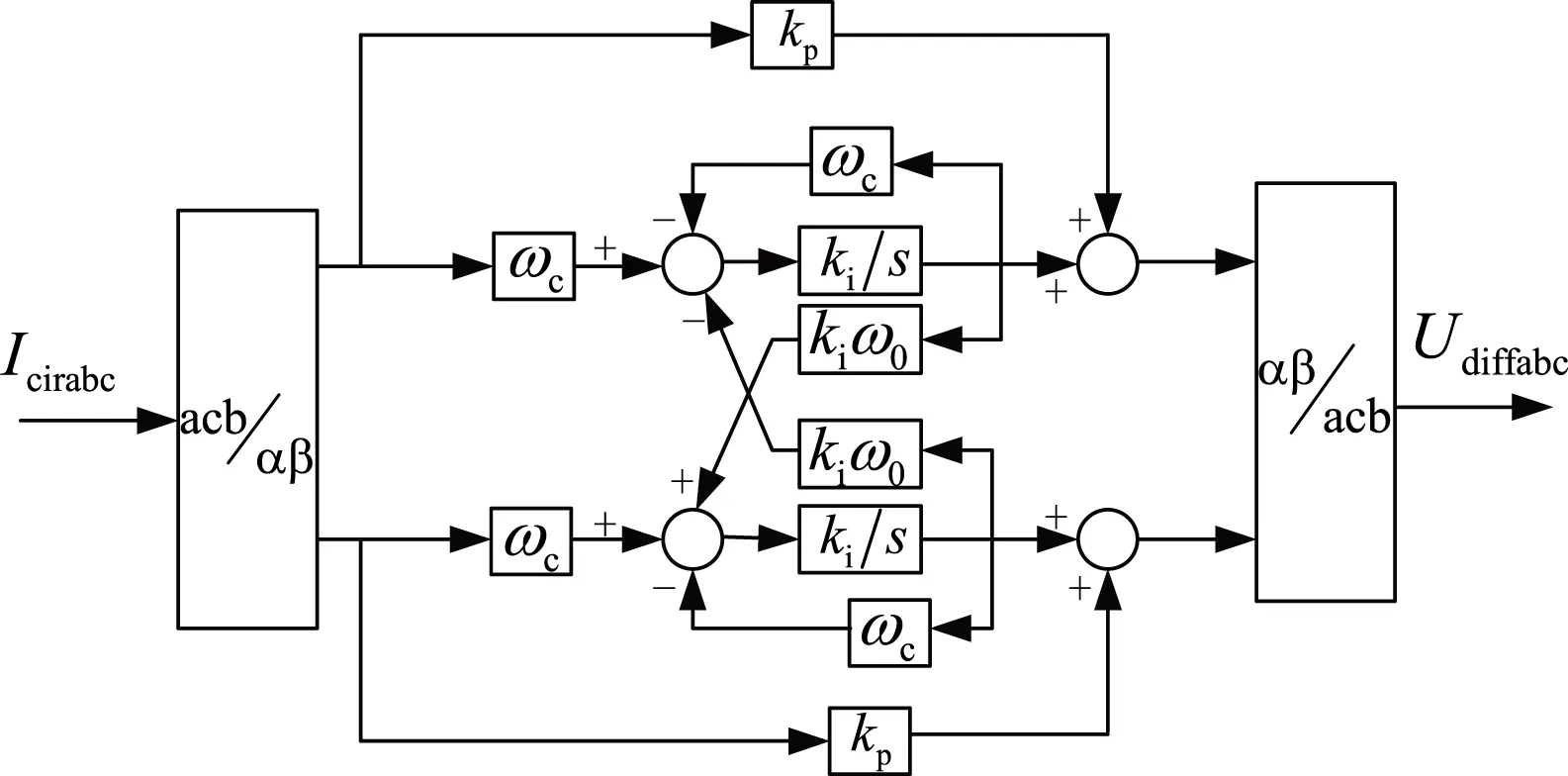
图6 比例降阶准谐振控制器框图

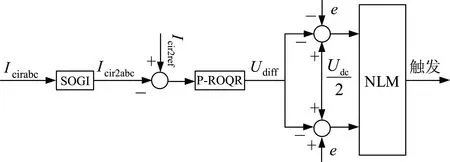
图7 环流抑制总体框图

2.3 降阶谐振的数字实现

对于降阶谐振控制器的数字实现，通常采用双线性变化[15]将s域表达式进行离散化设计，有

(21)

将式(21)带入到式(18)中，得到ROQR的离散化差分方程

yα(n)=yα(n-1)+kp[xα(n)-xα(n-1)]+

(22)

yβ(n)=yβ(n-1)+kp[xβ(n)-xβ(n-1)]+

(23)

3 仿真分析

为验证本文所提出的P-ROQR控制器的正确性，在PSCAD/EMTDC中搭建了11电平MMC-HVDC仿真模型,采用最近电平逼近调制策略(nearestlevelmodulation,NLM)。仿真系统参数见表1。

表1 MMC-HVDC仿真参数

控制器参数如表2。

表2 控制器参数

图8为加入P-ROQR环流控制器前后换流器A相环流对比，A相直流电流为0.25kA。从图中可以看出，未加入环流控制器时的环流峰值为0.38kA，其中二倍频环流占比52%；加入环流控制器后，峰值减小为0.27kA，占比8%。对比抑制前后环流幅值可以看出，二倍频环流占比明显减小，即加入环流控制器后，桥臂环流得到明显抑制。

图8 抑制前后环流对比

图9 A相环流傅立叶分析

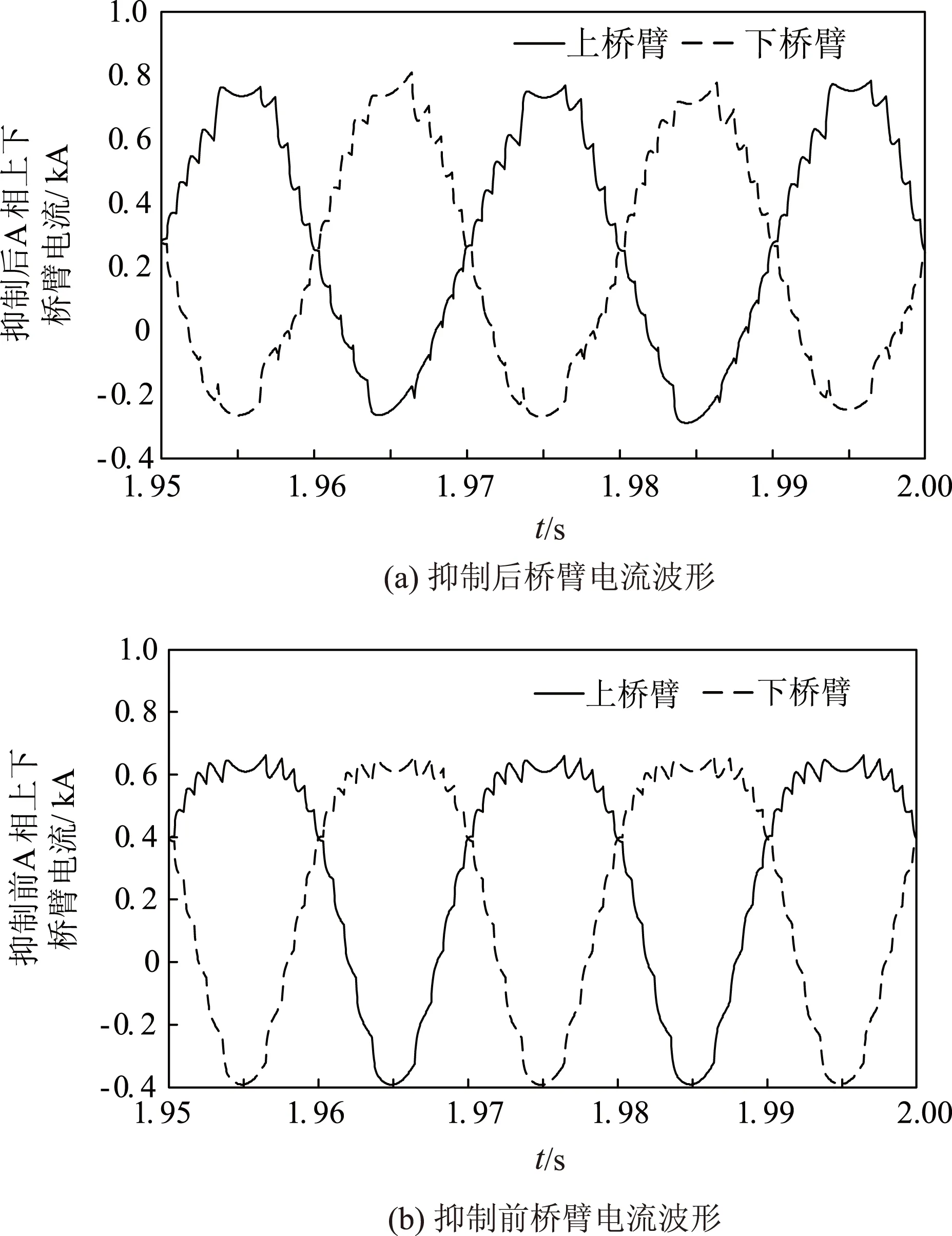
图10 抑制前后桥臂电流波形

对A相中的环流进行傅立叶分析并单独提取其二倍频分量如图9所示。

从图9中可以看出，在加入控制器后，控制器迅速响应，二倍频环流幅值显著减小，表明换流器三相环流中的二倍频分量得到明显抑制，有利于换流器稳定运行。

图10为加入环流控制器前后，换流器A相上下桥臂电流对比图。图10(a)为加入环流抑制时的桥臂电流波形，由于桥臂环流的存在，导致桥臂电流波形畸变；图10(b)为未加入环流抑制其后的桥臂电流波形，可以看出，在环流得到抑制后，桥臂电流重新恢复对称运行。

图11为A相桥臂子模块电压波形。对比抑制前后的电压波形，可以看出，加入环流抑制后桥臂子模块电压波动明显减小。

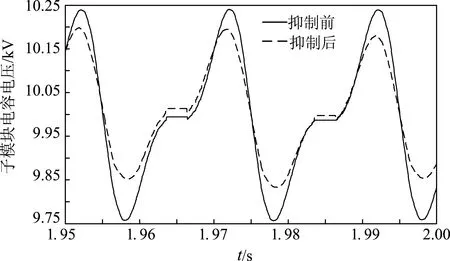
图11 桥臂子模块电容电压

4 结 论

本文简要分析了模块化多电平换流器环流的形成原因及通用抑制方法。然后提出了一种基于两相静止αβ坐标系的比例降阶准谐振环流控制器，并利用伯德图来分析该控制器的幅频特性，表明该控制器能有效准确跟踪特定频率谐波；再分析了其数字化实现方式，给出了降阶准谐振的离散化方程。最后，在PSCAD/EMTDC中搭建11电平仿真模型。仿真结果表明，该控制器能有效抑制MMC相间环流，减小桥臂电压不平量，降低桥臂子模块电容电压波动。

该控制器易于数字化实现，且参数调节简单，易于工程实现。

[1] 徐政，陈海荣.电压源换流器型直流输电技术综述[J].高电压技术，2007，33(1)：1-10.

[2] Lesnicar A, Marquardt R. An innovative modular multilevel converter topology suitable for a wide power range[C]//IEEE Power Tech Conference Proceeding. Bologna, Italy: IEEE, 2003:6.

[3] 屠卿瑞，徐政，郑翔，等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术，2010,36(2)：547-552.

[4] 周月宾，江道灼，郭捷，等.模块化多电平换流器子模块电容电压波动和内部环流分析[J].中国电机工程学报，2012,32(24)：8-14.

[5] 屠卿瑞，徐政，管敏渊，等.模块化多电平换流器环流抑制控制器设计[J].电力系统自动化，2010,34(18)：57-61,83

[6] 刘焕，岳伟，张一工，等.基于准比例-谐振控制的MMC-HVDC环流抑制策略[J].电力系统自动化，2015,39(12)：146-150.

[7] 苑宾，许建中，赵成勇，等.模块化多电平换流器

PR环流抑制器优化设计[J].中国电机工程学报，2015,35(10)：2567-2575.

[8] 班明飞，申科，王建赜，等.基于准比例谐振控制的MMC新型环流抑制器[J].电力系统自动化，2014,38(11)：85-89,129.

[9] Zhang Ming, Huang Long,Yao Wenxi, et al. Circulating harmonic current elimination of a CPS-PWM-based modular multilevel converter with a plug-in repetitive controller[J]. IEEE Transaction on Power Electonics, 2014,29(4):2083-2097.

[10]Li Binbin,Xu Dandan,Xu Dianguo. Ciculating current harmonics suppression for modular multilevel converters based on repetitive control[J]. Journal of Power Electronics, 2014,14(6):1100-1108.

[11]He Liqun, Zhang Kai,Xiong Jian, et al. A repetitive control scheme for harmonic suppression of circulating current in modular multilevel converters[J]. IEEE Transaction on Power Electronics, 2015, 30(1):471-481.

[12]阎发友，汤广福，贺之渊，等.一种适用于模块化多电平换流器的新型环流控制器[J].电力系统自动化，2014,38(1)：104-108,120.

[13]王朝明，王华广，王晴，等.基于双PI控制器的模块化多电平变换器环流抑制策略[J].电网技术，2014,38(10)：2905-2912.

[14]许富强，周迪青，付立，等.基于二阶广义积分器的谐波电流检测算法[J].水电能源科学，2012,30(5)：142-144，214.

[15]Alaoui A, Mohanmad A. Novel approach to analog-to-digital transforms[J]. IEEE Transactions on Circuits and Systems, 2007, 54(2):338-350.