输流微管的非线性强迫振动分析
2018-03-12滕英元杨天智沈阳航空航天大学航空航天工程学部沈阳110136
李 倩,滕英元,杨天智(沈阳航空航天大学 航空航天工程学部(院),沈阳 110136)
微纳米结构在通讯、航空航天、遥感等领域显示出了广泛的应用前景。众多国内外学者对微纳米结构的动力学特性展开了大量研究[1-3]。如杨帆[4]等通过表面能模型研究了表面效应对氧化锌悬臂梁力学性能的影响,结果表明表面效应使压电纳米梁刚度增强、感应电荷量减少。Jung[5]分析了矩形S型功能梯度纳米板简支模型的屈曲失稳。Kiani[6]等研究了双壁碳纳米管在不同边界条件下横向自由振动的动力学特征。Li[7]等人分析了磁、电及弹性地基的共同作用下纳米板的屈曲载荷和振动频率。
2002年,Yang[8]等人首次提出一种各向同性修正偶应力理论。该理论适用于各向同性材料。与经典偶应力理论不同,修正偶应力理论的应变与曲率张量均是对称的,因此极大地简化了材料参数数量。修正偶应力理论模型广泛应用于微纳米结构研究中,如Ma[9]等分析了基于修正偶应力的微尺寸Timoshenko梁模型的静态屈曲和自由振动特性。随后,考虑到中性层变形引起的几何非线性因素,Asghari[10]等基于修正偶应力理论研究了非线性Timoshenko梁的特性。Ansari[11]应用修正偶应力理论的Euler-Bernoulli梁模型分析了微梁的非线性振动,并与经典Euler-Bernoulli梁模型建模得到的结论进行了对比。值得一提的是,对于微纳米结构的理论提法尚未统一。修正偶应力理论、非局部弹性理论、应变梯度理论等均被应用于微纳米结构的研究中[12-15]。如Salamat[16]基于应变梯度理论,分析了表面能对微梁振动、屈曲等行为的影响。Ke[17]等人基于Kirchhoff板模型和非局部弹性原理,研究了受尺寸效应影响的磁电弹纳米板自由振动的固有频率及非局部参数、温度场、磁场、电场等对固有频率的影响。
修正偶应力理论也在近几年内被应用于流固耦合问题。对输流微、纳米管的动力学特性的准确建模和分析是流固耦合领域重要的研究课题。Ansari[18]研究了表面效应对功能梯度输流微壳的振动特性及动态稳定性的影响。Zhen[19]等研究了附加激振力影响下单壁碳纳米输流微管的非线性振动问题。Amiri[20]分析了磁场、电场、温度场等参数对磁电弹输流微管临界速度的影响。Yang[21]等研究了输流微管非线性自由振动的静态屈曲问题及尺寸效应对输流微管后屈曲的影响。但是从已有文献看,对输流微管非线性强迫振动的研究尚属空白。本文基于修正偶应力原理,应用直接多尺度法研究了输流微管的非线性强迫振动问题。
1 输流微管非线性强迫振动控制方程
微管及管内液体的质量分别用m和mf表示。L表示微管的长度,V表示流速,如图1所示。
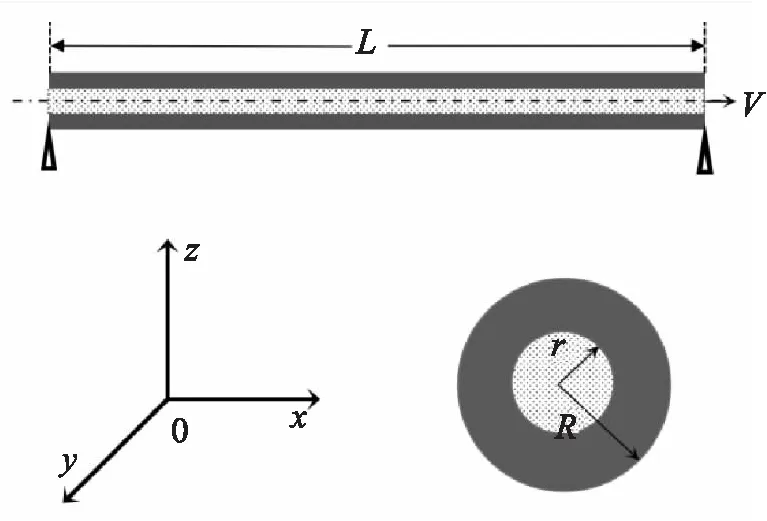
图1 输流微管示意图
x、y、z轴的位移ux、uy、uz分别表示为
ux=-zψ(x,t),uy=0,uz=w(x,t)
(1)
其中ψ表示中性轴转角
(2)
根据修正偶应力理论[8],应变能可表示为
(3)
σij=λtr(εij)δij+2Gεij;
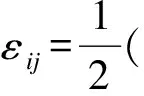

mij=2l2Gχij
(4)
其中,i,j=1,2,3。σij、εij分别表示应力张量和应变张量,χij是对称的曲率张量(即χij=χji),mij表示偶应力内力矩。λ表示弹性常数,δij是罗内克符号,G表示剪切模量,l为材料内禀参数。位移矢量和转动矢量用u和θi表示。其中θi表示为

(5)
根据式(1)~(5),可得到一维情况下输流微管的应变能
(6)
其中E是弹性模量,I是转动惯量,A是横截面面积。
本文考虑两端不可移动边界条件,因此管道的轴向变形可产生轴向拉力Nx,其势能为
(7)
式中轴向拉力Nx[19]具体表达为
(8)
微管的动能Tb表示为
(9)
管内液体的动能Tf为
(10)
由外场改变产生的势能为
(11)
其中P是由外场改变引起的附加轴向力,外场可以是力场、温度场、电磁场等。外部激励的变分表示为
(12)
F(x,t)表示外部激励力,其周期表达式为
F(x,t)=Bcos(ωt)
(13)
式中B表示激励幅值,ω为激励频率。
由哈密顿原理得
(14)
将式(6)~(13)代入式(14)中,非线性强迫振动控制方程为
(15)
本文考虑两端简支边界条件:
w(0,t)=w(L,t)=0,
(16)
引入无量纲表达式:
(17)
其中ε为小参数。
将式(17)代入(15)、(16)中,得到无量纲化控制方程为
(18)
无量纲化边界条件为
η(0,τ)=η(1,τ)=0,
(19)
2 输流微管线性固有频率
为了分析线性动力学特性,我们忽略非线性项,得到输流微管线性振动控制方程为
(20)
式(20)的解可设为
η=φn(x)eiωnτ
(21)
其中ωn为第n阶固有频率,φn为第n阶模态。
将式(21)代入式(20)中得到:
(22)
可设式(22)的解为
φn(x)=C1n(eiβ1nx+C2neiβ2nx+C3neiβ3nx+C4neiβ4nx)
(23)
其中βin(i=1,2,3,4)为式(22)的特征根,Cin(i=1,2,3,4)是式(22)解的系数。将式(23)代入式(22),得到:
(24)
两端简支条件的第n阶模态函数φn满足:
(25)
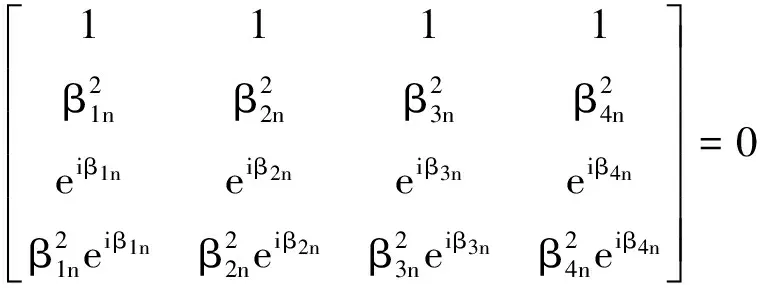
(26)
第n阶固有频率ωn可通过数值方法共同求解式(24)和(26)获得[22]。
3 直接多尺度法
用直接多尺度法求解输流微管非线性强迫振动控制方程(18),设其解为
η(ζ,τ,ε)=η0(ζ,T0,T1)+εη1(ζ,T0,T1)
(27)
其中η0、η1分别为快时间尺度位移函数和慢时间尺度位移函数,T0=τ表示快时间尺度,T1=ετ表示慢时间尺度。
将式(27)代入式(18)中,分离ε的同阶项:
(28)
(29)
式中Dn=∂/∂Tn,(n=0,1)。
式(28)的解设为
(30)
两端简支条件的振型函数φn(ζ)[23]表示为
(31)
将式(30)、(31)代入式(29)得
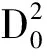
(32)
其中,cc为前面所有项的复共轭,NST为非长期项。
为分析共振点附近的响应,引入调谐函数σ得
ω=ωn+εσ
(33)
将(33)代入式(32),得到:
(34)
为消去长期项,可得到可解性条件为
(35)
其中
经过数值计算,χ是纯虚数,λ是复数。χ、λ可分别表示为
χ=iχI
λ=λR+iλI
(36)
振幅An用极坐标表示为
An=αn(T1)eiγn(T1)
(37)
共同求解式(35)~(37),分离实部、虚部得到:
(38)
式中θn=σT1-γn。
如果存在稳态响应,幅值an与相位θn必须是常数,应满足
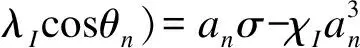
(39)
式(39)消去θn,可得到第n阶模态共振幅值an与调谐函数σ的解析关系为
(40)
4 数值结果与分析
本文算例选取以C304为材料的输流微管、水为管内流体的模型为研究对象,根据式(40)与表1、2给出的参数绘制共振时幅频响应曲线图,分析质量比、流速及附加轴向力对输流微管振动的影响。其中,ε=0.000 1,b=0.1,l=17.6 μm。

表1 几何参数
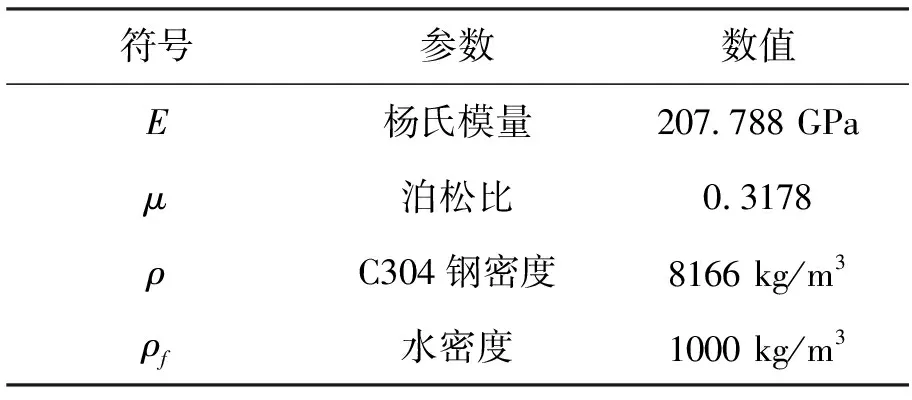
表2 材料参数
选取无量纲流速v=0.6、附加轴向力p=1.5,质量比β分别取0.826、0.857、0.903,得到幅频响应曲线如图2所示。由图2(a)可知,随质量比的增大,响应幅值增大。当质量比减小时,响应曲线逐渐向右偏转。对比图2(a)中一阶强迫共振图与图2(b)中二阶强迫共振图可知,二阶强迫共振图中曲线变化趋势与一阶强迫共振图基本一致。

图2 不同质量比对幅频响应曲线的影响
图3表示质量比β=0.857且p=1.5时,不同流速对幅频响应曲线的影响。从图3(a)可见,一阶强迫共振时,共振幅值随流速的增大而增大。流速越小幅频响应曲线向右偏转程度越大,多平衡解同时存在现象越明显。对比图3(a)、(b)可知,流速对二阶强迫共振与对一阶强迫共振的影响基本相同,即幅频响应曲线变化趋势基本一致。
选取β=0.857和流速v=0.6,分析附加轴向力分别为p=1.5、p=2、p=2.5的幅频响应曲线。由图4(a)、(b)可见,一阶强迫共振幅频响应曲线与二阶强迫共振幅频响应曲线形态基本一致,即不同附加轴向力的三条曲线变化趋势基本一致,但二阶强迫共振曲线比一阶强迫共振曲线偏转程度更明显。随外场引起的附加轴向力的增大,响应曲线向右弯曲程度增大。外场引起的附加轴向力越小,共振幅值越小。
当材料内禀参数l=0时,模型退化为经典的宏观Euler-Bernoulli梁振动模型。取β=0.857,v=0.6,p=1.5,绘制幅频响应曲线图,对比分析修正偶应力振动模型与经典宏观的Euler-Bernoulli梁振动模型的不同,如图5所示。

图3 不同流速对幅频响应曲线的影响
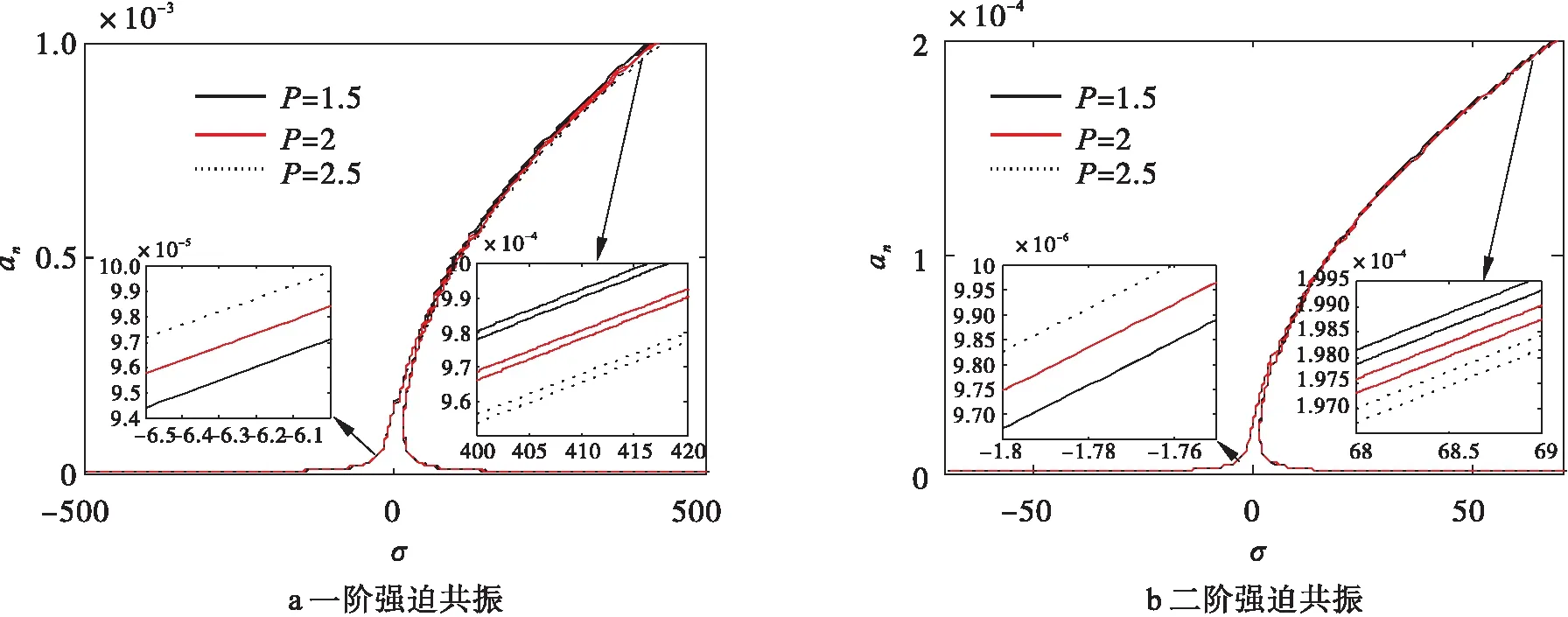
图4 不同外场引起的附加轴向力值对幅频响应曲线的影响
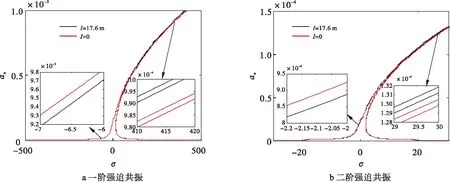
图5 两种模型的幅频响应曲线
观察图5可知,l=0时响应曲线的共振幅值大于l=17.6 μm时响应曲线的共振幅值,即经典模型的共振幅值大于修正偶应力模型的共振幅值。经典模型响应曲线向右偏转程度大于修正偶应力模型响应曲线,经典模型的多平衡解同时存在现象更明显。对比图5(a)与图5(b),一阶强迫共振与二阶强迫共振曲线变化的趋势基本相同,二阶强迫共振时曲线的偏转程度更明显。
5 结论
本文基于Euler-Bernoulli梁模型和修正偶应力理论,建立两端简支输流微管非线性强迫振动模型。该模型考虑轴向变形引起的几何非线性及外场引起的附加轴向力的影响。根据哈密顿原理推导出微分控制方程。利用直接多尺度法得到了共振时稳态响应的幅频关系,该模型可退化为经典Euler-Bernoulli梁振动模型。结合数值算例绘出输流微管强迫共振时的幅频响应曲线,通过幅频响应曲线图详细分析了质量比、流速、附加轴向力等参数对系统振动的影响,并对比了经典Euler-Bernoulli梁振动模型与该振动模型的不同。研究结果表明,一阶强迫共振幅频响应曲线与二阶强迫共振幅频响应曲线变化趋势基本一致;共振幅值随质量比、流速、附加轴向力的减小而减小;增大附加轴向力或减小流速、质量比时,曲线向右偏转程度增大,多平衡解同时存在现象更明显;修正偶应力振动模型较经典Euler-Bernoulli梁振动模型共振幅值减小,幅频响应曲线向右弯曲程度减小。
[1] ROQUE C M C,FIDALGO D S,FERREIRA A J M,et al.A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method[J].Composite Structures,2013,96(4):532-537.
[2] MOHAMMAD ABADI M,DANESHMEHR A R.An investigation of modified couple stress theory in buckling analysis of micro composite laminated Euler-Bernoulli and Timoshenko beams[J].International Journal of Engineering Science,2014,75(2):40-53.
[3] SHAAT M,MAHMOUD F F,GAO X L,et al.Size-dependent bending analysis of Kirchhoff nano-plates based on a modified couple-stress theory including surface effects[J].International Journal of Mechanical Sciences,2013,79(1):31-37.
[4] 杨帆.表面效应对压电纳米梁弯曲行为的影响[J].电子元件与材料,2016,35(8):46-49.
[5] JUNG W Y,HAN S H,PARK W T.Amodified couple stress theory for buckling analysis of S-FGM nanoplates embedded in Pasternak elastic medium[J].CompositesPart B Engineering,2014,60(2):746-756.
[6] KIANI K.Vibration analysis of elastically restrained double-walled carbon nanotubes on elastic foundation subjected to axial load using nonlocal shear deformable beam theories[J].International Journal of Mechanical Sciences,2013,68(2):16-34.
[7] LI Y S,CAI Z Y,SHI S Y.Bucking and free vibration of magnetoelectroelasticnonplate based on nonlocal theory[J].Composite Structures,2014,111(1):522-529.
[8] YANG F,CHONG A C M,LAM DCC,et al.Couple stress based strain gradient theory for elasticity[J].International Journal of Solids and Structures,2002,39(10):2731-2743.
[9] MA H M,GAO X L,REDDY J N.A microstructure-dependent Timoshenko beam model based on a modified couple stress theory[J].Journal of the Mechanic and Physics of Solids,2008,56(12):3379-3391.
[10]ASGHARI M,KAHROBAIYAN M,AHMADIAN M.A nonlinear Tomishenko beam formulation based on modified couple stress theory[J].International Journal of Engineering Science,2010,48:1749-1761.
[11]ANSARI R,ASHRAFI M A,ARJANGPAY A.An exact solution for vibrations of postbuckled microscale beams based on the modified couple stress theory[J].Applied Mathematical Modeling,2014,39(10-11):3050-3062.
[12]DEHROUYEH-SEMNANI A M,DEHROUYEH M,TORABI-KAFSHGARI M,et al.A damped sandwich beam model based on symmetric-deviatoric couple stress theory[J].International Journal of Engineering Science,2015,92:83-94.
[13]SALAMAT-TALAB M,SHAHABI F,ASSADIA.Size dependent analysis of functionally graded microbeams using strain gradient elasticity incorporated with surface energy[J].Applied Mathematical Modelling,2013,37(1-2):507-526.
[14]ANSARI R,GHOLAMI R,SHOJAEI M F,et al.Size-dependent bending,buckling and free vibration of functionally graded Timoshenko microbeams based on the most general strain gradient theory[J].Composite Structures,2013,100(5):385-397.
[15]VAEZIM,SHIRBANI M M,HAJNAYEB A.Free vibration analysis of magneto-electro-elastic microbeams subjected to magneto-electric loads[J].PhysicaE:Low-dimensional Systems and Nanostructures,2016,75:280-286.
[16]KE L L,WANG Y S.Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory[J].Act Mechanica Sinica,2014,30(4):516-525.
[17]SALAMAT-TALAB M,SHAHABI F,ASSADIA.Size dependent analysis of functionally graded microbeams using strain gradient elasticity incorporated with surface energy[J].Applied Mathematical Modelling,2013,37(1-2):507-526.
[18]KE L L,WANG Y S.Free vibration of size-dependent magneto-electro-elastic nanoplates based on the nonlocal theory[J].Acta MechanicaSinica,2014,30(4):516-525.
[19]ANSARI R,GHOLAMI R,NOROUZZADEH A,et al.Size-dependent vibration and instability of fluid-conveying functionally graded microshells based on the modified couple stress theory[J].Microfluidics and Nanofluidics,2015,19(3):509-522.
[20]ZHEN Y X,FANG B.Nonlinear vibration of fluid-conveying single-walled carbon nanotubes under harmonic excitation[J].International Journal of Non-Linear Mechanics,2015,76:48-55.
[21]AMIRI A,POURNAKI I J,JAFARZADEH E,et.al.Vibration and instability of fluid-conveyed smart micro-tubes based on magneto-electro-elasticity beam model[J].Microfluidics and Nanofluidics,2016,20(2):1-10.
[22]YANG T Z,JI S,YANG X D,et al.Microfluid-induced nonlinear free vibration of microtubes[J].International Journal of Engineering Science,2014,76(4):47-55.
[23]杨天智.复杂约束输流管道的稳定性与分岔[D].沈阳:沈阳航空工业学院,2007.
[24]ÖZ H R,PAKDEMIRLI M.Vibrations of an axially moving beam with time-dependent velocity[J].Journal of Sound and Vibration,1999,227(2):239-257.
