基于忆阻器的鉴相电路设计与分析
2018-03-12,,,,
,, ,,
(1.太原学院 计算机工程系,山西 太原 030032;2.中北大学 动态测试省部共建实验室,山西 太原 030051)
鉴相电路是指能够测量输入信号的相位差的电路,它是锁相环的重要组成部分,同时在一些测量电路中鉴相电路也有非常重要的应用,例如相位式激光测距仪中,可以通过测量两路信号的相位差来获得距离信息,目前应用最为广泛的鉴相器为数字式的,主要有Conventional PFD,precharged PFD等,但这些方法都存在死区,过充等缺陷[1].根据电路理论中的逻辑完整性,蔡少棠提出了根据电荷和磁通量关系定义的第四种基本元件忆阻器[2].近年来,在忆阻器在应用方面的研究取得了广泛的进展,目前这些研究主要集中于:存储器、神经网络、混沌电路等方面[3~6].忆阻器具有体积小、功耗低、便于集成等优点,利用忆阻器的特性,本文提出一种基于忆阻器的鉴相电路.
1 惠普忆阻模型理论

图1 惠普物理模型
惠普模型是最早被提出的忆阻器模型,应用较为普遍,是目前最被业内认可的模型之一.其物理模型如图 1所示[7].
该模型采用三明治结构,由两个Pt电极夹着两层薄膜结构构成,其中一层为TiO2,这一层是不导电的,另一层为缺少约0.5%氧原子的TiO2层,表示为 TiO2-x,这一层具有导电性.在忆阻器上加正向电压时,TiO2-x层中的氧空位向TiO2层中漂移,使部分TiO2转化为TiO2-x,TiO2-x层的厚度增加,整个器件表现为阻值减小.同理,当施加反向电压时,整个器件的表现为阻值增大.图1中,D表示TiO2和 TiO2-x的总厚度,W表示TiO2-x层的厚度.当W=D的时候,忆阻器阻值最小,用RON表示,当W=0时,忆阻器阻值为最大,用ROFF表示.根据这一模型,可以将忆阻器的阻值定义为(公式1)所示形式.
Rm(t)=ROFF+(RON-ROFF)x
(1)
其中,x是TiO2-x层的厚度与总厚度的比值,可表示为:
x=ω/D
(2)
在掺杂区宽度一定时,电子在其内部的迁移速度由公式(3)决定.
(3)
式(3)中,η=±1,分别对应在忆阻器两端施加正、反向电压时的情形.μD为半导体中的电子在单位电压下的迁移速度,其值约为10-10cm2V-1s-1,i(t)为t时刻的电流大小.

对(3)两边积分可得(4).
(4)
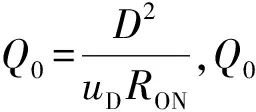
将(4)代入(1)可得公式(5),其中ΔR=RON-ROFF.
(5)
根据欧姆定理,u(t)=Rm(t)i(t),由(5)可得:
(6)
取q(0)=0,解此微分方程可得:
(7)
其中Φ(t)是通过忆阻器的磁通量.
在忆阻器边界上会发生非线性的离子漂移,为使得模型更加接近实际,在(3)的右侧乘上不同的窗函数,得到(8).
(8)
其中:w(x)是非线性的窗函数,这里使用的窗函数为1-(2x-1)2p,该函数是目前较常用的窗函数之一[8].在该函数的作下,离子在到边界处时,移动速度减小为0.
将(8)代入(2)中,p取1时,通过求解微分方程,得到(9).
(9)
由(9)可知,忆阻值是由电荷量决定的,而电荷量是t的函数,所以当忆阻器参数一定时,两者是一个确定的函数关系.
2 忆阻器的Simulink模型及特性验证
根据(1)、(3)、(8)构建忆阻器的Simulink模型如图2所示,采用的窗函数为1-(2x-1)2p.

图2 忆阻器Simulink模型

图3 电压、电流滞回特性曲线
仿真实验中的具体参数如下:初始状态x0取0.1,RON取100,ROFF100 kΩ,P取1,忆阻器上所加的信号为频率为30 kHZ的正弦恒流信号,仿真时间30 ms.仿真得到图3所示.从图3中可以看出:当施加的信号正向增大时,随着流过忆阻的磁通量的增大,器件阻值减小,在电压达到峰值前,曲线斜率逐渐增大;电压达到峰值后,曲线斜率逐渐减小,忆阻器的阻值增大,该模型所构成的器件具有电流和电压滞回特性,符合忆阻器的特性要求.
3 鉴相电路设计与仿真
3.1 鉴相电路设计与分析
相位差存在于电压或电流信号中,可以使用填脉冲法、傅立叶变换等对其进行测量.这些方法一般都是将被测信号与参考信号的相位差转换成一定宽度的脉冲,通过测量脉冲宽度来获得相位差,技术的核心难点在于对脉冲宽度进行测量[9].这里设计了如图4所示的基于忆阻器的鉴相电路.
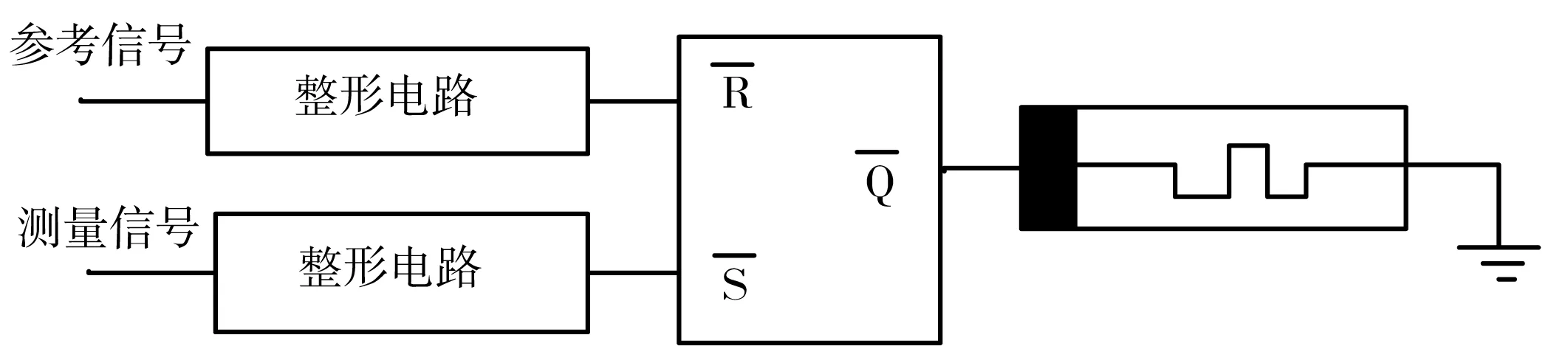
图4 忆阻器的鉴相电路组成结构框图
这里假设输入信号为正弦信号,参考信号与测量信号经过整形之后转换成脉冲信号,两路方波信号输入到RS触发器,RS触发器将两路输入的信号相位差转换成一路脉冲信号输出.脉冲的宽度与相位差成正比,因此,只需要测量方波信号的宽度即可得到相应的相位差.
这里被测的相位差被转换成了相应时间长度的脉冲信号,即等效成是相应时间长度的直流信号.当忆阻器两端所加的信号恒流流信号,即电流为常数I时,

这里考虑施加正向激励,即η取1的情况,由(9)得(10).
(10)
所以(1)可转换为(11).
(11)
对(11)第2个因子分子,分母乘以D+ω0[exp(-It/Q0)-1]得:
(12)
这里为了表示简洁,设{D+ω0[exp(4It/Q0)-1]}{D+ω0[exp(-4It/Q0)-1]}=ξ,由于电流是有限的,Q0是一个较大的量,当时间较短时,ξ近似等于D,整理得(13).
(13)
(14)
由(14)可知,在忆阻器两端施加恒流信号,当忽略式中非线性项时,忆阻器电阻值与信号的施加时间呈线性关系,但是由于式中仍含有与D和ω0的差相关的丰富的非线性项,当输入信号为脉冲信号时,忆阻器的输出是非线性的.
3.2 系统仿真
这里通过图4模型对系统进行仿真,忆阻器参数取如下:RON取100,ROFF取100 kΩ,P取1,取x0=0.5,参考信号与测量信号均为频率为16 kHz的正弦信号,相位差为π,其时域波形如图5(a)所示,参考信号与测量信号经过整形之后转换成方波信号如图5(b)所示,方波信号输出如图5(c)所示,忆阻值随时间的变化如图5(d)所示.

图5 仿真结果
由图5可知,相位差转换成了忆阻器的变化量,通过忆阻器阻值的测量可以间接得到脉冲的宽度,即实现鉴相.系统是非线性的,对图5(d)中0到31.25 us内输入输出特性曲线进行最小二乘法拟合,可求得其非线性误差为3.43%.由于窗函数的存在,忆阻器在边界上的非线性效应非常明显,非线性误差会进一步增大,当取x0=0.9时,其他参数不变时,仿真求得其非线性误差增加到9.82%.
4 结论
本文在分析忆阻器原理的基础上,建立了忆阻器Simulink模型,设计了基于该模型的忆阻器鉴相电路,并进行了分析与仿真,通过仿真验证了理论分析的正确性,该电路能够将被测相位转换成相应的电阻值变化,但由于忆阻器在边界上的非线性效应非常明显,该鉴相器在使用时,其测量范围与精度将受到系统非线性效应的影响.
