多尺度单特征谱分割算法*

张敬茂，沈艳霞

江南大学 物联网技术与应用教育部工程研究中心，江苏 无锡 214122

1 引言

图像分割是图像理解的关键步骤之一[1-2]，将输入图像分割为不相交的连贯区域，从中提取整个区域的特征信息，减小分析的计算消耗。针对图像分割，已经提出了很多优秀的图像分割算法，主要分为两类：不基于图的算法，如均值漂移算法[3]、EM（expectation-maximization）[4]和基于图的算法[5-9]。与不基于图的算法相比，基于图的算法能够自适应地权衡局部相似关系[10]。

规范割（normalized cut，Ncut）算法是一种广泛应用的基于谱图理论的谱分割算法。在图像分割中，Ncut能够同时权衡类内相似性和类间不相似性，并且可以近似为广义特征向量问题。使用Ncut进行图像分割时，关于图的相似矩阵对图像分割结果有很大的影响。目前，为了提高谱分割效果，已有很多研究对该相似矩阵的构建进行改进。一种方法是结合图像中像素点（或者超点）的不同特征信息构建相似矩阵[11-13]。例如文献[12]结合4种特征信息即超点的均值和方差、像素点的颜色和边缘信息构建相似矩阵；文献[13]考虑结合多种局部轮廓信息，如亮度、颜色和纹理差异、结构森林轮廓等。另一种方法是对输入图像进行多层分解，或者结合不同的分解方法对图像进行分解[14-17]，然后利用分解后的图构建相似矩阵。文献[15]对图像进行多层分解，并以此构建多尺度相似矩阵；文献[16]和文献[17]利用不同的方法对图像进行分解，然后利用分解图构建相似矩阵。无论利用不同图像不同特征信息，还是对图像进行不同的分解，都有多种组合特征信息和分解图的方式。然而在实际应用中，确定使用哪种方式是个复杂的过程，尤其是在核磁共振影像（MRI），合成孔径雷达影像（synthetic aperture radar，SAR）等应用领域，无法提供颜色信息，此时根据颜色特征信息改进的算法就不适用，因此有必要考虑从相似矩阵中提取多尺度特征，构建新的相似矩阵，提高使用单一特征信息时谱分割的效果。

目前，扩散映射（diffusion map）在三维形状分析[18]、图像表示[19]、语言识别[20]等许多领域得到广泛应用。扩散映射能够提取出输入图像的本质几何描述，对像素点来说，即以该点为中心的所有几何结构的局部信息。基于扩散映射[21]，本文定义了一种多尺度特征描述器（diffusion map based multiscale feature descriptor，DMFD）。然后，建立扩散映射与谱图小波[22]的关系，利用谱图小波中切比雪夫多项式算法进行快速计算，避免计算输入图像DMFD全部特征值和特征向量的问题。最后，构建基于DMFD的谱分割算法，提出一种能够自适应选择最优尺度计算相似矩阵的方法，避免执行算法时选择尺度的过程。

2 基于扩散映射的多尺度特征描述器

Coifman等人[21]根据马尔科夫随机游走定义了扩散映射。对于输入图像G，包含N个像素点，根据其特征信息构建的相似矩阵为A，对角矩阵转移矩阵P=D-1A，矩阵P的特征值和特征向量分别为 (λl)l=0,1,…,N-1和 (χl)l=0,1,…,N-1，则扩散映射定义为：

其中，c表示尺度参数；g(∙)表示关于特征值的函数。

给定像素点a，根据以上定义，定义基于扩散映射的多尺度特征描述器为：

在给定尺度c下，像素点之间的距离采用欧氏距离度量，即：

式（3）也被称为扩散距离[21]。

如上所述，计算DMFD及扩散距离的步骤如算法1。

算法1计算DMFD与扩散距离

输入：图，尺度。

（1）对输入图像提取每个像素点的特征信息，利用这些特征构建相似矩阵；

（2）根据相似矩阵，计算转移矩阵P；

（3）计算转移矩阵P的特征值 (λl)l=0,1,…,N-1和特征向量 (χl)l=0,1,…,N-1；

（4）根据式（1）和式（2）计算所有点的DMFD；

（5）根据式（3）计算扩散距离。

3 快速计算算法

由式（1）和式（2）可知，对于尺寸为m×n的输入图像，需要计算DMFD的mn个特征值和特征向量。例如Berkeley数据库中图像尺寸为321×481，则需要对维度为N2(N=154 401)的矩阵进行特征分解，计算N个特征向量和特征值，这在实际应用中是不现实的。考虑到谱图小波的定义与特征值和特征向量有密切关系，并且存在快速计算谱图小波的切比雪夫多项式算法，建立谱图小波与扩散映射之间的关系，利用切比雪夫多项式算法来快速计算DMFD，避免对所有特征值和特征向量的计算。

由式（1）和式（3）可得：

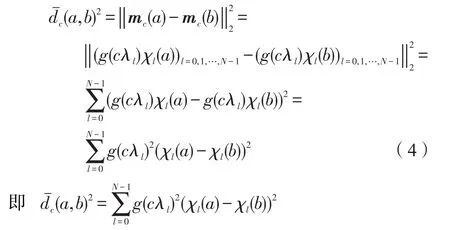
谱图小波中，在尺度c下，以a点为中心的基函数定义为：

由式（5）计算欧氏距离为：

根据文献[21]，在平方可积测量空间(X,μ)中，式（6）可根据式（5）写为如下形式。

4 多尺度单特征谱分割算法

下文首先定义算法的流程，然后分析其在实际应用时的不足，并提出一种自适应尺度选择方法解决该问题。

4.1 基于DMFD的多尺度单特征谱分割

Ncut作为被广泛应用的谱分割算法，其相似矩阵尺寸为N2，然而对于一般电脑来说，无法计算和存储该矩阵。为此，将图像分割为超点，提取超点的特征信息计算相似矩阵A。本文使用两种特征信息，即颜色和纹理。对于颜色特征，采用RGB和HSV颜色空间，计算两个超点间的26种颜色距离[1,23]dcolor；对于纹理特征，采用超点间的64种纹理差异[1,24]dtexture。提取超点的特征信息后，首先构建相似矩阵A和转移矩阵P。其中Aij=exp(-dcolor/σd)或Aij=exp(-dtexture/σd)。计算扩散映射、DMFD以及dc(a,b)后，利用提出的特征描述器计算超点之间的相似性度量：

进而构成相似矩阵S。

基于DMFD的多尺度单特征谱分割算法（DMFDNcut）可描述如算法2。

算法2DMFD-Ncut

输入：图，k，尺度c。

输出：分割图像。

（1）对输入图像进行超点分割，并对超点提取单一特征信息，如颜色、纹理等；

（2）利用提取的特征信息构建相似矩阵A和转移矩阵P；

（3）由式（2）计算DMFD，并由式（6）计算式（3），得到距离度量；

（4）根据式（8）计算相似矩阵S及拉式矩阵

（5）计算L的前k个特征向量，构成新的特征空间；

（6）由k-means算法对k个特征向量构成的特征空间进行聚类，得到图像分割结果。

4.2 自适应尺度选择

在执行DMFD-Ncut时，需要指定尺度，然后对输入图像在指定尺度下进行分割。DMFD-Ncut虽然可以让用户指定分割尺度，但是得到分割结果后才能判断哪个尺度更为合适。这无疑为算法执行增加了困难。因此，本文提出一种逐点自适应确定最优尺度（pointwise self-adaptive optimal scale，PSOS）的方法，在分割之前确定最优尺度。

图方差[15]可用来判断相似向量携带的信息量，图方差越大，携带的信息量越大。因此，本文使用图方差作为判断最优尺度的方法。假设输入图像的相似矩阵为S，a为图像的第i个点，则Sa=Si∙表示以a为中心的所有相似度量值。图方差定义如下：

考虑上述自适应最优尺度选择方法，DMFDNcut算法可更新为算法3。

算法3自适应DMFD-Ncut（PSOS）

输入：图，k，尺度集C。

输出：分割图像。

（1）对输入图像进行超点分割，并对超点提取单一特征信息，如颜色、纹理等；

（2）利用提取的特征信息构建相似矩阵A和转移矩阵P；

（3）由式（2）计算DMFD，并由式（6）计算式（3），得到距离度量；

（4）根据式（8）计算相似矩阵S；

（5）使用式（9）计算图方差，选取最优尺度；

（6）使用式（10）对相似矩阵进行更新，并计算相应拉式矩阵

（7）计算L的前k个特征向量，构成新的特征空间；

（8）由k-means算法对k个特征向量构成的特征空间进行聚类，得到图像分割结果。

5 实验分析

为了验证本文提出的算法，在真实数据集上进行实验，并对DMFD-Ncut和 DMFD-Ncut（PSOS）进行分析，对比这两种算法的差别。具体数据选择、参数设置及结果对比如下文所述。

5.1 参数设置

本文算法与使用单一特征信息构建相似矩阵的Ncut算法（Ncut_color，Ncut_texture）进行对比。实验采用Berkeley图像分割数据库（BSD300），该数据库包含测试集（100幅图）和训练集（200幅图）。根据实验及经验，对于灰度特征取σd=1；对于颜色特征取σd=1；对于纹理特征取σd=15。对于灰度信息，选取尺度c={10,15,20,25,30,35}；对于颜色和纹理信息，选取尺度c={20,25,30}。Ncut_color与Ncut_texture的相似矩阵使用Aij=exp(-dcolor/σd)和Aij=exp(-dtexture/σd)分别计算。取4个参数对图像分割结果进行量化评估，分别为 F-measure（F）、Segmentation Covering（Covering）、Probabilistic Rand Index（PRI）、Variation of Information（VOI）[14]。其中，F-measure度量边缘分割效果。对每个量化评估参数，使用两种度量方式：ODS（optimal dataset scale），对所有图像使用固定参数进行分割；OIS（optimal image scale），对每个图像选取最优分割参数。为了计算这两种度量方式，本文将ODS和OIS中使用的参数设置为图像的分割数目，k={2,3,…,40}。

5.2 实验结果

表1为使用颜色和纹理特征的量化评估结果，最优结果用粗体标注。其中Ours_color和Ours_texture为DMFD-Ncut在所有3个尺度下的最优结果；PSOS_color和PSOS_texture为使用自适应最优尺度选择方法的评估结果。从表1中可以看出，在使用单一特征信息进行图像分割时，本文提出的算法相对于原Ncut算法，几乎在所有的评估结果中，都显示了对分割结果明显的优势。在只使用灰度信息时，DMFD-Ncut的ODS评估与Ncut大部分相同，OIS评估则优于Ncut。而在实际应用时，往往只会对单独的一幅图片进行分割，从这方面考虑，OIS评估更能反映出算法的应用价值。尽管在使用PSOS方法时，因为式（10）对两点取平均导致图像分割结果与直接使用DMFD-Ncut时相同或略有降低，但PSOS方法的大部分结果依然优于原Ncut算法。因此，使用PSOS方法可避免尺度选择的过程，但直接使用DMFD-Ncut可取得更为优秀或相同的分割结果。

图1和图2对颜色和纹理分别提供了视觉结果对比。

（1）颜色

图1选取人、动物、植物3类图进行对比。在所有的3幅图中，DMFD-Ncut能够在k=10时将显著目标分割出来，而Ncut_color则无法识别。在细节方面，如图（1）中，DMFD-Ncut在k=20时就可以将人、帆船、海分割出来，而Ncut_color则一直无法将三者完全分割；图（2）、（3）中，DMFD-Ncut始终能较完整地将鸟与蘑菇识别出来，而Ncut_color在分割数增加时，将背景和目标物都进行不适当的分割。以上说明，DMFD能够提供更加本质的特征描述，从而提升图像分割效果。

（2）纹理

图2选取人、动物、建筑进行对比。在图像背景复杂（图（1）、（3））或背景简单（图（2））时，DMFDNcut都能够尽量将符合视觉直觉的区域分割到一类，得到较满意的分割结果。如图（1），DMFD-Ncut完美地将路面分为一类，且将人识别出来，而Ncut_texture将路面过分割。而图（3）中，随着分割数k增加，DMFD-Ncut仍能将船以及建筑物识别出来，而Ncut_texture倾向于将目标过分割。这说明，在使用纹理特征时，DMFD仍能对图像提供更为本质的特征描述。

图3为使用颜色特征时，利用PSOS方法的图像分割结果与不同尺度下DMFD-Ncut分割结果对比。如图所示，PSOS方法可以将最优的尺度选取出来。如小丑鱼部分，使用PSOS方法可以将小丑鱼较完整地分割出来。但是在背景的珊瑚部分，使用PSOS的分割效果比尺度为25时差，但是优于尺度为30时的结果。这是因为计算PSOS相似矩阵的公式（10）对逐点的最优结果取平均导致的。因此，使用PSOS方法可避免尺度选择的过程，但直接使用DMFD-Ncut可取得更为优秀或相同的分割结果。

Table 1 Quantitative evaluation on BSD300表1 BSD300量化评估结果

Fig.1 Comparison of segmentation results on color图1 使用颜色特征的分割结果对比

5.3 运行时间

图4为在给定尺度c下，随着相似矩阵尺寸N的变化，对一个像素点计算扩散映射的时间对比。其中N=100,150,200,…,5 000 ，“diffusion map”表示未使用快速计算方法时的时间曲线，“DMFD”表示使用快速计算方法时的时间曲线。当相似矩阵尺寸不大时，如N＜1 000时，两者相差不大；但是随着N变大，本文方法计算时间明显低于直接计算扩散映射所用时间。

图5为本文算法运行时间与Ncut算法运行时间的对比，随机选取20幅图片，设置分割数目k=30。其中“+”表示Ncut运行时间，“◆”表示 DMFD-Ncut运行时间，“o”表示PSOS DMFD-Ncut运行时间。DMFD-Ncut在单尺度下运行，PSOS DMFD-Ncut则选取3个尺度进行自适应选择。如图所示，在大部分数据上，DMFD-Ncut和PSOS DMFD-Ncut运行时间小于Ncut，而在小部分情况下PSOS DMFD-Ncut运行时间远高于其余两种算法，这是因为需要在不同尺度中自适应地选择合适的尺度，并根据待选择尺度的多少，运行时间也会有所变化。

Fig.2 Comparison of segmentation results on texture图2 使用纹理特征的分割结果对比

6 结束语

使用谱分割算法进行图像分割时，无论使用多特征融合还是图分解方法，都是十分复杂的，尤其是在某些应用领域如MRI影像、SAR影像等，无法提供某些特征如颜色，因此本文提出一种基于扩散映射的多尺度特征描述器（DMFD），提高使用单一特征信息下，谱分割在图像分割上的效果。DMFD可以描述输入图像更为本质的结构，为后续谱分割过程提供更为本质的特征描述。为了使DMFD在实际应用中可行，本文建立了扩散映射与谱图小波的关系，利用谱图小波中的切比雪夫多项式算法快速计算DMFD，避免了扩散映射必须计算全部特征值和特征向量的问题。基于DMFD，构建了相应谱分割算法DMFD-Ncut，提出了一种能够自适应选择最优尺度计算相似矩阵的方法，避免了执行算法时选择尺度的过程。实验显示，DMFD-Ncut和使用自适应尺度选择方法的DMFD-Ncut都能够显著提升使用单一特征的Ncut在图像分割中的效果。然而使用超点分割解决Ncut计算量大的问题，使得图像分割结果过分依赖于超点分割的效果，下一步工作将集中研究适用于DMFD-Ncut的快速计算方法。

Fig.3 Comparison of segmentation results with PSOS and DMFD-Ncut图3 使用PSOS的图像分割结果与不同尺度DMFD-Ncut结果对比

Fig.5 Comparison of running time with different algorithms图5 不同算法运行时间对比

[1]Kim S,Nowozin S,Kohli P,et al.Higher-order correlation clustering for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,36:1761-1774.

[2]Mobahi H,Rao S R,Yang A Y,et al.Segmentation of natural images by texture and boundary compression[J].International Journal of Computer Vision,2011,95(1):86-98.

[3]Comaniciu D,Meer P.Mean shift:a robust approach toward feature space analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(5):603-619.

[4]Carson C,Belongie S,Greenspan H,et al.Blobworld:image segmentation using expectation-maximization and its application to image querying[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,24(8):1026-1038.

[5]Yuan Yonghua,Li Yu,Zhao Xuemei.High-resolution panchromatic remote sensing image segmentation based on spectral clustering[J].Chinese Journal of Scientific Instrument,2016,37(7):1656-1664.

[6]Yang Nongying,Li Feng,Gui Yan.Repeated texture elements extraction from texture images[J].Journal of Frontiers of Computer Science and Technology,2016,10(8):1154-1165.

[7]Shi Jianbo,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.

[8]Benson A R,Gleich D F,Leskovec J.Tensor spectral clustering for partitioning higher-order network structures[C]//Proceedings of the 2015 International Conference on Data Mining,Vancouver,Apr 30-May 2,2015.Philadelphia:SIAM,2015:118-126.

[9]Aytekin Ç,Ozan E C,Kiranyaz S,et al.Extended quantum cuts for unsupervised salient object extraction[J].Multimedia Tools andApplications,2017,76(8):10443-10463.

[10]Estrada F J,Jepson A D.Benchmarking image segmentation algorithms[J].International Journal of Computer Vision,2009,85(2):167-181.

[11]Rohkohl C,Engel K.Efficient image segmentation using pairwise pixel similarities[C]//LNCS 4713:Proceedings of the 29th Annual Symposium of the German Association for Pattern Recognition,Heidelberg,Sep 12-14,2007.Berlin,Heidelberg:Springer,2007:254-263.

[12]Li Xiang,Jin Lianghai,Song Enmin,et al.An integrated similarity metric for graph-based color image segmentation[J].Multimedia Tools and Applications,2016,75(6):2969-2987.

[13]Pont-Tuset J,Arbeláez P,Barron J T,et al.Multiscale combinatorial grouping for image segmentation and object proposal generation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,39(1):128-140.

[14]Arbelaez P,Maire M,Fowlkes C C,et al.Contour detection and hierarchical image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(5):898-916.

[15]Cour T,Bénézit F,Shi Jianbo.Spectral segmentation with multiscale graph decomposition[C]//Proceedings of the 2005 Conference on Computer Vision and Pattern Recognition,San Diego,Jun 20-26,2005.Washington:IEEE Computer Society,2005,2:1124-1131.

[16]Kim T H,Lee K M,Lee S U.Learning full pairwise affinities for spectral segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(7):1690-1703.

[17]Wang Xiaofang,Tang Yuxing,Masnou S,et al.A global/local affinity graph for image segmentation[J].IEEE Transactions on Image Processing,2015,24(4):1399-1411.

[18]Sidi O,van Kaick O,Kleiman Y,et al.Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering[J].ACM Transactions on Graphics,2011,30(6):126.

[19]Seo D,Ho J,Vemuri B C.Covariant image representation with applications to classification problems in medical imaging[J].International Journal of Computer Vision,2016,116(2):190-209.

[20]Keller Y,Coifman R R,Lafon S,et al.Audio-visual group recognition using diffusion maps[J].IEEE Transactions on Signal Processing,2010,58(1):403-413.

[21]Coifman R R,Lafon S.Diffusion maps[J].Applied and Computational HarmonicAnalysis,2006,21(1):5-30.

[22]Hammond D K,Vandergheynst P,Gribonval R.Wavelets on graphs via spectral graph theory[J].Applied and Computational HarmonicAnalysis,2011,30(2):129-150.

[23]Pele O,Werman M.Fast and robust earth mover's distances[C]//Proceedings of the 12th International Conference on Computer Vision,Kyoto,Sep 27-Oct 4,2009.Washington:IEEE Computer Society,2009:460-467.

[24]Leung T,Malik J.Representing and recognizing the visual appearance of materials using three-dimensional textons[J].International Journal of Computer Vision,2001,43(1):29-44.

附中文参考文献：

[5]袁永华,李玉,赵雪梅.基于谱聚类的高分辨率全色遥感影像分割[J].仪器仪表学报,2016,37(7):1656-1664.

[6]杨弄影,李峰,桂彦.纹理图像中重复纹理元素提取方法[J].计算机科学与探索,2016,10(8):1154-1165.