声模态对超声破碎空化场的影响

冯丽丽 刘 斌 吴 雪 徐雪冬 李子路

(1. 北京工商大学材料与机械工程学院，北京 100048；2. 中机康元粮油装备有限公司，北京 100083)

超声破碎是利用液体介质中的超声场，对其中的固体颗粒或生物组织等实施破碎的过程。声空化效应是超声破碎的主要作用机理，增强空化效应，提高超声利用能效是超声应用的重要研究内容之一。

为提高料腔内的空化场效应，增大空化作用范围，目前多数采用频率为20 kHz的超声[1]。现有的超声波破碎形式多采用浸入式变幅杆结构，料腔以定体积槽式或柱状容器为主，料液采用批量处理方式。破碎效能的提高通常采用增大输入功率或采用大振幅变幅杆[2-4]，导致能耗和体积不断加大。已有研究者从料腔声场的几何特性考虑空化场分布。Klíma等[5]研究了声源频率在20 kHz时的料腔几何对声强分布的影响并对其尺寸进行了优化，提高了空化作用体积。虽然发现了优化后的几何上存在2个较强的空化区，却未考虑料液声场和器壁边界条件的影响。Wang等[6]则采用了一种Langevin型压电换能器，研究结果发现位于变幅杆辐射面处的锥形空化效应的局域结构，对于有限功率条件下如何扩大空化效应作用范围尚未提及。

从声学场能利用的角度来看，超声空化效应的产生和增强是由超声源、料液材质、腔体大小和边界条件(声场条件)共同作用的结果，因此空化效应的增强不仅要提高源强，同时要考虑声源与声场的耦合作用，利用定容空间的声模态效应使得超声能量的转化更为高效。声模态表征了某一声场条件下的声波传播的固有规律，应用试验方法较难获取，需引入有限元法以弥补试验法的不足。

本试验以20 kHz浸入式超声破碎装置为研究对象，结合声学有限元和测试分析，研究了声模态特性对定容空间超声能量的分布影响。通过考察液位高度、声源位置、边界条件等因素，以期获取超声破碎场内空化能的最优分布，实现更为高效的超声能量转化方式及破碎效果，可为超声技术工业化应用中的声源与容腔匹配提供技术参考。

1 材料与方法

1.1 材料与仪器

超声波破碎装置：变幅杆直径6.5 mm，标称频率20 kHz，中科院声学所定制；

水听器：CS-1型，灵敏度3.162 3×10-5V/Pa，丹麦B&K公司；

数字示波器：TDS 2024B型，200 MHz带宽，取样率2 GS/s，美国泰克公司；

激光测振系统：由OFV-505型激光头和OFV-5000型振动仪组成，德国Polytec公司；

工业相机：MotionBLITZ cube4型，高速CMOS传感器，在550 nm处的光灵敏度为1 600 bit/lux-sec，参考电压1 V，光谱带宽400～800 nm，最大分辨率1 280(H)×1 024(V)，最大帧率93 000 fps，焦距50 mm，光圈0.95，德国MIKROTRON公司；

单联型新闻灯：QH-1300w-1型，电压220 V，电流6 A，色温3 200 K，温州市长城影视器材有限公司；

料腔容器：壁厚2 mm的玻璃烧杯，料液选用去离子水以减少杂质对空化的影响。

1.2 声场理论分析

声场中，均匀的理想流体介质中小振幅声波的波动方程可表示为[7-8]：

(1)

式中：

▽2——拉普拉斯算子；

c——料液中声速，m/s；

p——瞬时声压，Pa；

t——时间，s。

超声破碎料腔为柱状体，假定液面和料腔壁均为软边界条件，声压可表示为柱贝塞尔函数解与驻波解的组合形式：

pmm=AmmJmm(kmmr)sin(kzz)ejωt|m=0，

(2)

式中：

A——与幅值有关的常数项；

k——波数；

m——声波周向传播模态相关的数值，本试验采用轴对称声源，取m为0；

n——声波径向传播模态相关数值，取正整数；

Jm(kmnr)——代表宗量为(kmnr)的m阶柱贝塞尔函数；

ω——角频率，rad/s；

z、r——分别为柱坐标系的中心轴线方向和径向方向。

根据已知边界条件和声源位置特性，可得：J0(k0na)=0。待定常数k0n、kz满足以下条件：

(3)

(4)

(5)

式中：

q——声波沿轴线传播模态相关数值，取正整数；

a——料腔半径，mm；

H——液位高度，mm；

j0n——0阶柱贝塞尔函数的第n个根值。

由式(3)～(5)可得到料腔各阶声模态所对应的液位高度：

(6)

相关研究[9]表明，超声场中液位的高度对其中空化场的分布影响显著。当边界条件、声源和料液物性一定时，超声源工作频率与料腔声场的谐振频率(声模态频率)一致，可强化空化效应并增大空化作用面积。

为反映料腔声场的能量分布，可采用平均声能量密度，即单位体积里的平均声能量：

(7)

式中：

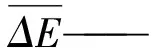
V——体积元在声扰动之前的体积，m3。

1.3 试验方法

1.3.1 变幅杆端面振速及工作频率的测定 变幅杆端面振速采用激光测振法。在工况条件下，激光测振仪获取变幅杆端面中心振速，并将其输入到数字示波器，示波器同步采集变幅杆的工作频率，通过数据端口与计算机连接，进行显示、存储、分析处理。

1.3.2 料腔声场的有限元模型 根据圆柱烧杯的形状，料腔声场为圆柱形，工况时去除变幅杆的浸入体积，有限元的建模与分析采用COMSOL软件。料液的声学特性取值：设定水密度ρ为1 000 kg/m3，声速c取1 480 m/s。边界条件：变幅杆侧面与料液接触面为硬边界条件，料液面为空气层(声压反射系数为0.999 7)，料腔壁为薄壁玻璃，可视为软边界条件。声源条件：变幅杆端面法向振速应用实测数据。网格划分：根据COMSOL轴对称计算条件，采用二维四边形面网格，单元尺寸最大为3.98 mm，计算上限频率约为62 kHz，满足频率精度计算要求。

1.3.3 超声空化场图像采集及料腔声场测试 采用柱状全透明玻璃容器，为观察清晰，采用全黑背景。工况条件下，工业相机架设于料液容器正前方，距离容器轴心75 mm，使用侧上方45°强光照射。

玻璃柱状容器采用3点悬置支撑，使底部壁面与圆周壁面具有相同的软边界条件。试验前采用清水浸泡法清除换能器、变幅杆和水听器表面脏物，避免表面脏物所引起的稳态气泡产生[10]。水听器[11-12]按指定测点位置布放于料液中，超声变幅杆稳定工作后，依次对各测点进行声压数据采集，并确保各测点的工况条件一致。测试系统简图如图1所示。

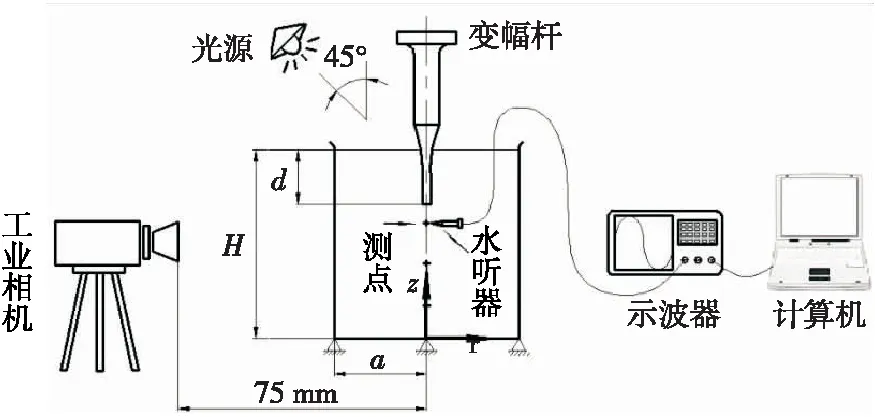
图1 测试系统简图Figure 1 Plot of test system diagram

2 结果与分析

2.1 变幅杆工况频率及振速

料腔容器中换能器的谐振频率受到容器中的物料容量、工作发热、与料腔壁的耦合等因素影响会发生频率漂移现象[13]，为保证仿真与试验的有效性，需要获得工况频率下超声变幅杆的振速幅值。功放的工况电流为40，70 mA时的超声变幅杆的振速频谱图如图2所示。

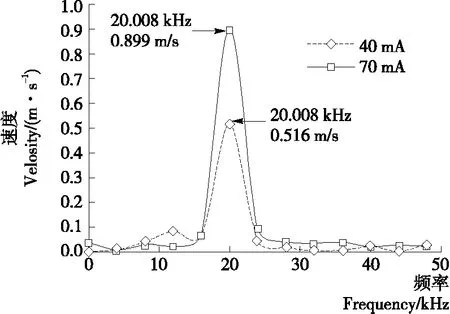
图2 变幅杆振速频谱图Figure 2 Plot of vibration amplitude spectrum of the horn

图2表明，标称频率为20 kHz的换能器，实际工作频率为20.008 kHz，两者相对误差仅为0.04%，工况频率误差对空化效应及平均声能量密度影响的量化研究影响极小，可将工况频率视为20 kHz。工况频率为20 kHz时，变幅杆端面纵向振动，振速达到最大，功放的工况电流在40，70 mA时变幅杆最大振速分别为0.516，0.899 m/s。

2.2 料腔声场的有限元分析

根据超声破碎的能效利用及处理能力，选择半径42 mm的料腔，并取n=1的柱贝塞尔函数解(高阶解时，径传播的声压幅值衰减较大)。以声源的工作频率20 kHz作为声模态的参考频率，由式(6)分别求得q为1，2时的液位高度，分别是50，100 mm。考察3种液位高度下的声传播特性(变幅杆浸入深度5 mm，功放70 mA)，以获取工况频率20 kHz声能分布的优化料腔溶剂。

20 kHz声源激励时3种液位高度料腔声压分布云图如图3所示。在相同声源条件下，液位高度为50，100 mm的料腔具有与工况频率相似的声模态，能形成谐振声场，其声压的分布云图表现为声模态云图，高幅值声压的传播呈扩散式区域分布。液位高度为50 mm时，声压云图分布呈轴对称单椭圆形，声压幅值由中心向外扩散衰减，至壁面边界处为0；液位高度为100 m时，声压云图分布呈轴对称双椭圆形，双椭圆为上下对称，对称面位于料腔液位高度的1/2处，声压幅值由双椭圆中心向外扩散衰减，至壁面边界处为0，且该对称面处声压也为0。液位高度为80 mm时，声压分布呈现为端部局域效应，即在变幅杆端部附近声压幅值较大，远离变幅杆后，声压幅值迅速衰减，且最大声压幅值远小于谐振液位50，100 mm的。

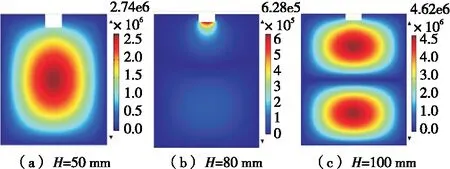
图3 3种液位高度下的绝对声压Figure 3 Absolute sound pressure at three levels

图3中的3种液位高度的前两阶模态(高阶模态>>20 kHz，不再列出)如表1所示。液位高度为50 mm时，料腔声场的一阶声模态为19.891 kHz，液位高度为100 mm时料腔的二阶声模态为19.968 Hz，与工况频率接近，可形成谐振料腔声场。由表1可知，图3(a)和(c)分别为50,100 mm液位的一、二阶谐振声场的声压云图分布，声压幅值具有扩散放大效应。液位高度为80 mm时，一、二阶声模态均与工况频率偏差较大，不能形成谐振，如图3(b)所示，表现高声压幅值区域集中在声源附近，远端传播快速衰减至极低幅值。

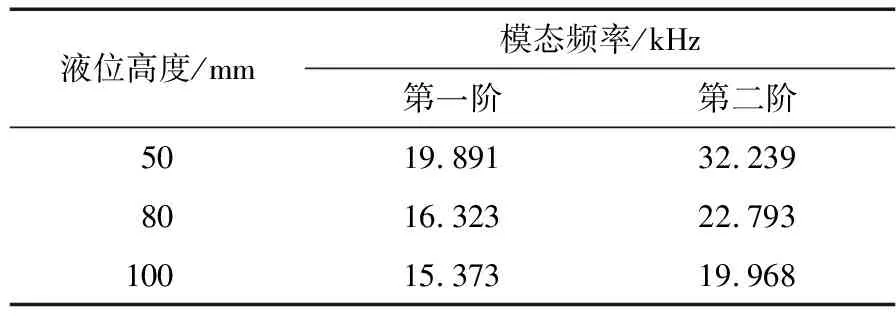
表1 3种液位高度下的前两阶模态Table 1 The first two modes under three kinds of level

2.3 变幅杆浸入深度的影响

变幅杆浸入深度不但表征了超声声源在声场的位置特性，同时由于浸入深度的不同，使得料腔声场体积发生变化，会直接导致料腔声场的声模态及声压分布规律，因此需要进一步分析和探讨。当浸入深度不大(<30 mm)时，由于变幅杆直径较小，浸入深度的体积占有率在料腔体积中较小，对声模态的影响较小，不再探讨。

料腔半径42 mm，液位高度100 mm，声源激励20 kHz，功放70 mA，变幅杆浸入深度按5 mm增量进行取值，如图4(a)所示。对5～30 mm时料腔轴线方向的声压分布进行仿真分析，结果如图4(b)所示。

图4(b)表明，当浸入深度为15 mm时，声压幅值放大效应最为显著，远大于其他浸入深度；浸入深度不同不影响声压分布特性，声压幅值的最大值出现在距底面1/4和3/4液位高度位置处，距底面1/2液位高度和液位高度边界位置处，其绝对声压为0。图4(a)的声压云图分布也表明，浸入深度只改变声场中的声压幅值大小，声压云图分布形状不受影响，即由此产生的空化能分布并无改变。

为了验证仿真分析，对料腔轴线方向的声压分布进行了

图4 不同浸入深度下的绝对声压Figure 4 The absolute sound pressure at different immersion depths

测试(变幅杆浸入深度10 mm)，为消除绝对幅值差异性影响，采用归一化处理进行对比。由图5可知实测结果与仿真值基本吻合，工况条件下实测结果较好地反映了谐振声场的声压变化趋势。图5中声压测试曲线与仿真结果略有差异，主要由于超声空化的出现导致声辐射能力降低，使得实测声压分布位置略低于仿真分析位置。

2.4 空化效应与声压分布的对比

超声破碎中空化场分布特性与料液中超声能量的分布密切相关，因此在仿真分析中采用平均声能密度来表示空化效应的空间分布特性。不同液位条件下，超声破碎空化场分布图像与场内平均声能密度分布的仿真云图对比如图6所示。

图6(a)～(c)表明，工况频率下破碎声场内的能量分布特性与空化效应密切相关。当液位高度为50，100 mm时，料腔达到谐振液位条件，声场具有与工况频率吻合的声模态，料腔产生谐振效果，声能的辐射大大提高，而80 mm的液位高度则无此效果。声能辐射的量级表明，谐振液位的声能密度幅值远大于非谐振液位条件。空化效应的分布图像较好地验证仿真结果：谐振液位50 mm与非谐振液位80 mm 相比，尽管空化域大小相似，谐振液位50 mm形成了与谐振声能分布相仿的远场空化效应，而非谐振液位80 mm只表现出声源附近的近场空化能力。谐振液位100 mm时不但空化域大小有所增强，更表现与谐振声能分布相仿的近场及远场的空化能力。

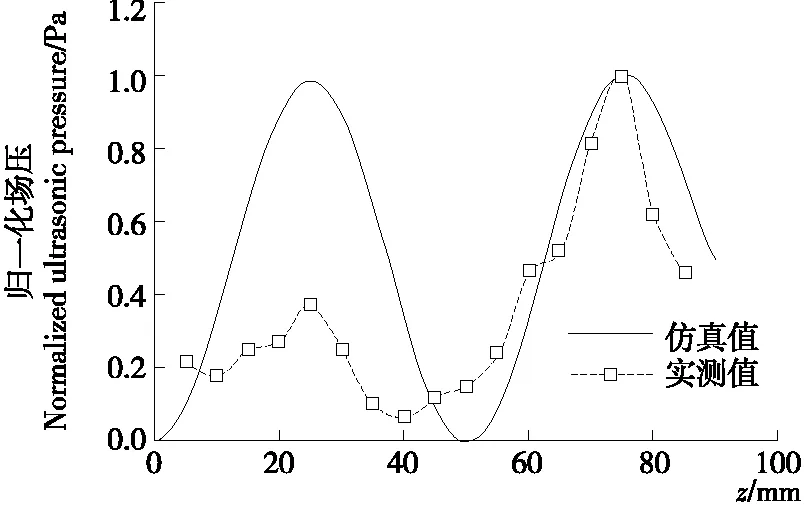
图5 实测值与仿真值的归一化声压曲线Figure 5 Plot of normalized sound pressure for experimen-tal measurements and simulation

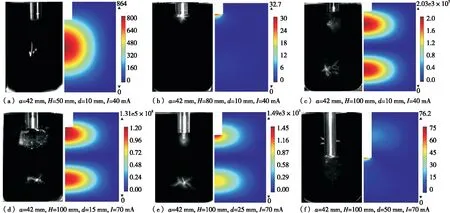
图6 超声破碎空化场分布图像与场内平均声能密度分布的仿真云图对比情况Figure 6 Comparison of the simulated cloud image of the distribution of ultrasonic crushing cavitation field and the distribution of the average sound energy density in the field

图6(d)～(f)表明，谐振液位100 mm时，声源的不同浸入深度对空化域大小影响显著。在相同声源功率条件下，声源的不同浸入深度对场内平均声能密度分布无明显影响，即料腔声场的模态特性变化受变幅杆浸入体积的影响较小，但平均声能密度的幅值变化非常显著。随着声源浸入深度变大，平均声能密度的幅值逐渐增大，浸入深度15 mm时幅值接近最大，此时空化效应大大增强，如图6(d)所示。浸入继续增加，平均声能密度的幅值呈下降趋势，当深度到达50 mm 时平均声能密度幅值接近最小。料腔中空化分布的试验结果也较好地验证了场内声能的分布特性。

3 结论

(1) 应用有限元分析方法，分析了定容料腔声场的声模态特性。以半径42 mm圆柱形料腔为例，根据其工况声源频率、实际边界条件和料液材质，应用声模态法可以确定其谐振液位(一、二阶)高度分别为50，100 mm，确定谐振液位为增强场内声能辐射效率提供了理论分析基础。

(2) 对于定容料腔声场而言，液位高度对声场内能量分布影响显著。当声源功率相同时，非谐振液位下平均声能密度幅值受限，且空化效应分布于声源附近，作用区域有限，远场空化能力弱；谐振液位下平均声能密度幅值大大增加(大约为非谐振液位的25～60倍)，空化效应显著增强，空化区域呈现稳定的空间分布，且表现出明显的远场空化能力。

(3) 在谐振液位条件下，声源的浸入深度也是影响声能密度幅值与空化效应的重要因素。浸入深度的变化对场内声能及空化的空间分布影响较小，对声能幅值和空化域的大小影响显著。浸入深度为声波第一峰值附近时，声能幅值接近最大，空化域面积增大。浸入深度为声波第一波节处时，声能幅值接近最小，空化域面积极大地减少。

本试验研究了柱形料腔中超声空化能的空间分布，尚未涉及料腔形状、功率变化、多声源等因素的影响，后续研究在考虑上述因素基础上，对声源与容腔器形的耦合、大振幅非线性效应、多声源匹配进行深入探讨，实现超声破碎应用中能量效率转化的高效与可控。