基于量子退火Metropolis-Hastings算法的叠前随机反演

张广智 赵 晨 涂奇催 刘 江 张佳佳 裴忠林

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②海洋国家实验室海洋矿产资源评价与探测技术功能实验室，山东青岛 266071； ③中海石油(中国)有限公司上海分公司，上海 200030)

1 引言

地震反演可以分为确定性反演与随机反演两大类。与传统的确定性反演方法相比，随机反演对于具有薄层特征的油气藏识别具有一定优势[1]。随机地震反演方法的技术关键是分析并拟合储层地球物理特性的分布规律并对不同地球物理参数进行研究，以此获得这些参数与地层岩性的关系[2]。随机反演方法可以同时拟合实际地震观测数据和测井数据，且可以有效地利用测井数据中所包含的高频信息提高反演的分辨率[3,4]。

作为常用的反演方法，马尔科夫链蒙特卡洛方法(MCMC)可以获得后验概率密度的一系列样本，通过对这些样本进行统计分析，可以获得满足要求的反演结果。基于Metropolis算法[5]，Hasting[6]提出了Metropolis-Hastings (MH)算法，是最常用的MCMC方法； Smith等[7]首次提出利用MCMC方法获取参数反演的后验分布； Alberto等[8]利用直流电阻率测深数据反演一维地球模型，首次将MCMC方法应用于完全非线性反演问题； Chen等[9]发现MCMC反演方法能提供大量与未知参数有关的全局信息，与确定性反演方法相比，能得到更好的估计值； 朱嵩等[10]提出了动态多链搜索策略，在多链并行的过程中，通过逐步减少链的数目提高算法的计算效率；张广智等[11]研究了基于MCMC方法的叠后及叠前地震反演方法； 李远等[12]将Haario等[13,14]提出的AM-MCMC方法引入地震反演，主要通过修改候选值的产生方式来提高算法的收敛效率； 张广智等[15]、Pan等[16]将AM (Adaptive Metropolis)策略与DR(Delayed Rejection)策略相结合，提出了AMDR-MCMC算法，将DR策略融入AM策略，克服AM策略过度依赖初始协方差的劣势。综合前人研究成果，可以发现传统的MCMC算法较为依赖初始模型及搜索策略,当计算时间有限或搜索策略设置不当时,对于一个较为复杂的参数空间,MH算法往往不能对反演参数空间进行充分的搜索。

针对该问题，前人借鉴量子退火最优化思想对传统的MH方法进行改进。魏超等[17]依据模拟退火算法与量子蒙特卡洛理论，提出量子退火最优化算法(QA)，并利用简单的单道模型数据进行了验证;Alulaiw等[18]将基于QA算法的反演方法应用于实际工区。量子退火算法的核心在于通过引入Hamilton量的概念修改模拟退火的接受概率。因此，同样对MH算法的接受概率形式进行修改，引入一个逐渐减小的正变量调整状态接受的概率，提高算法的稳定性和收敛性。本文借鉴量子退火算法的改进措施，提出了量子退火MH算法，并将其应用于叠前随机反演。利用测井数据，获取反演参数的先验信息，利用反演参数的正演关系构建似然函数，利用量子退火MH算法对后验概率密度进行抽样，得到最终的反演结果。

2 理论与方法

在贝叶斯理论框架下，通过先验信息及似然函数构建与后验概率密度相关的目标函数，利用量子退火MH算法进行反演，得到反演结果。

2.1 MH算法

MCMC方法的核心是构造一个平稳分布且与所求后验分布相同的马尔科夫链，反复迭代至平稳状态，从而得到后验分布的样本，再基于这些样本做各种统计、推断[19]。

MH方法的主要步骤为：首先由建议分布q(xt,x*)产生一个潜在的转移xt→x*，然后根据概率α(xt,x*)来决定是否接受。从[0,1]的均匀分布上抽取随机数u，则马尔科夫链下一时刻的状态为[20]

(1)

式中：t表示马尔科夫链的当前时刻；xt表示在时刻t的值；x*表示由建议分布产生的候选抽样值；α(xt,x*)代表转移核函数，常用的形式为

(2)

式中，π指马尔科夫链平稳分布表达式。

当目标分布取为似然函数L(x)，且建议分布为对称分布时，则式(2)可改写为

(3)

因此，对于反演问题，MH算法的接受概率可改写为

α(xt,x*)=exp{min[0,g(x*)-g(xt)]}

(4)

式中g表示所构建的目标函数。

经过多次迭代，可以获得后验概率分布的一系列样本，对这些样本进行筛选，可获得满足要求的反演结果。

如搜索策略设置不当，传统的MH算法收敛速度较慢。由于搜索策略的设置需要针对不同问题具体分析，因此很难找到最佳的搜索策略。本文利用量子退火MH算法应对搜索策略的问题。

2.2 量子退火MH算法

为提高反演算法的效率与精度，参照量子退火最优化方法，改进MH算法，提出量子退火MH算法，该方法的基础在于Hamilton量的引入。

当有外力作用于体系，此时系统的Hamilton量H为

(5)

将目标函数之差ΔE=E(m(l+1))-E(m(l))看作体系的动能H0，则

H=ΔE+CΓ(t)

(6)

式中C为常数。

量子最优化算法利用系统的Hamilton量表达式替换传统的模拟退火算法中的目标函数之差，CΓ(t)的引入使迭代的反演结果在接近模型参数时依旧存在一定的接受概率，快速接近最优结果[21]。

量子退火算法属于全局随机搜索的最优化算法，能有效避免线性化反演的缺陷，具有较大的发展潜力[22]，然而其接受概率最终趋近于0，因此仅能获得唯一的反演结果，无法对反演结果进行不确定性分析；MH算法可获得收敛于后验概率分布的一系列反演结果的样本，因此可以对反演结果进行不确定性分析。因此，依据量子退火算法的改进思想将式(4)改写为

α(xt,x*)

(7)

式中φ是一个随着迭代次数增加而逐渐趋近于0的较小的正变量。

对于量子退火MH算法来说，φ的引入可以适当减少当前状态不必要的转移，使马尔科夫链能够更加快速、稳定地收敛于后验概率密度，避免局部极值的出现。

参照传统的MH算法，量子退火MH算法的实现流程见图1，其中“rand”为0～1之间的随机数。其与MH算法的主要区别在于新的量子退火MH算法采用了新的接受概率表达形式。

中国矿业大学（北京）是煤炭特色高等教育的全国重点院校，拥有我国首家以能源与安全为特色的科技园——“中关村能源与安全科技园”和“中国矿业大学留学人员创业园”，并与北京市共建能源安全产业技术研究院，组成了学校产学研用及科技成果转化体系；另外科技园就位于校内，学生不需要高频校外甚至异地往返，避免了学校频繁组织交通车、组织成本高且可能存在安全等方面的问题，为创建校企合作的煤矿特色机械虚拟仿真实验平台提供了地理和资源的双重优势。

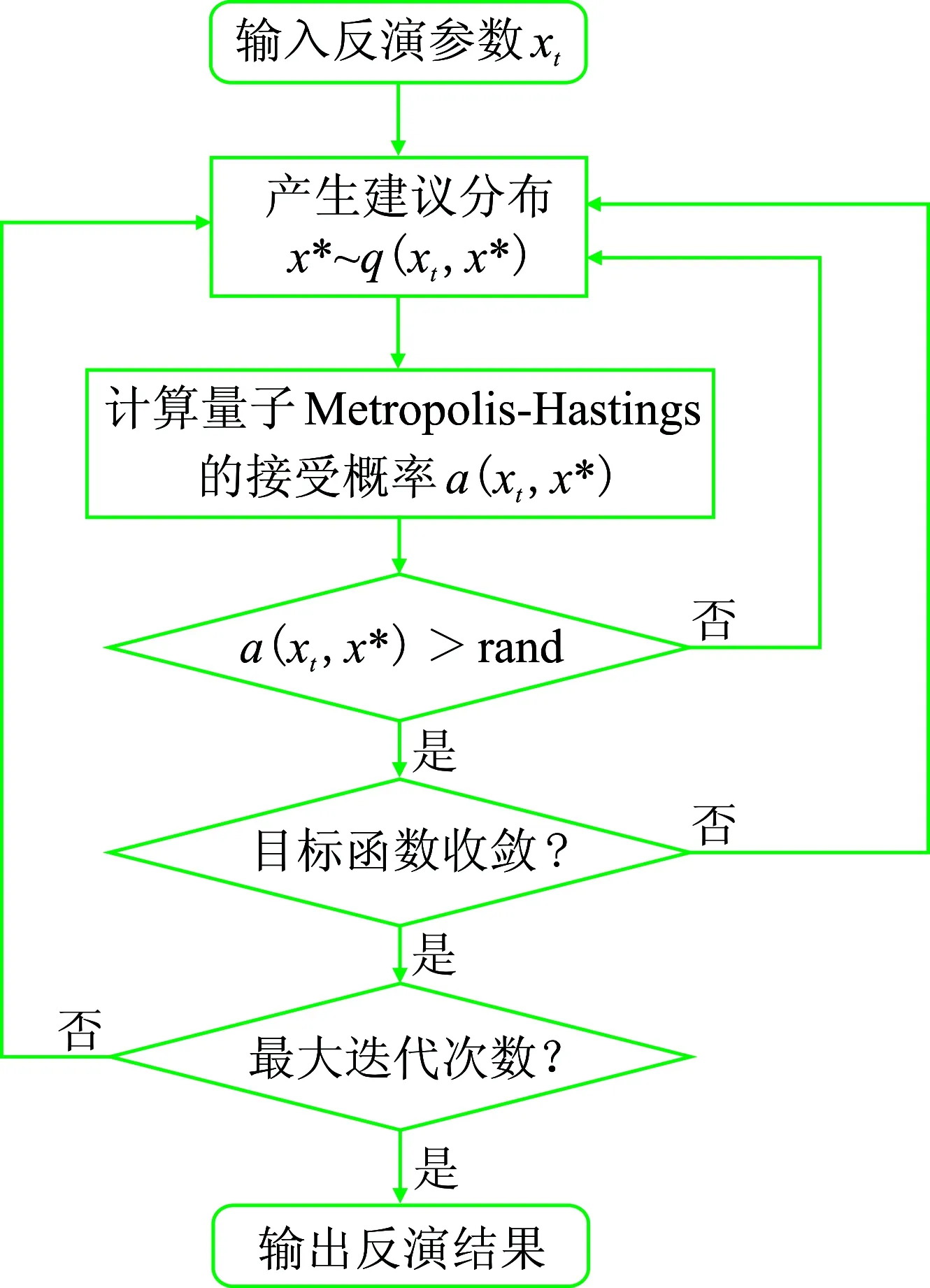
图1 量子退火MH算法流程图

2.3 基于量子退火MH算法的叠前反演方法

叠后地震反演只能获得地下阻抗的相关信息，对于较为复杂的地层，传统的叠后反演无法有效识别岩性及流体，且叠后反演是基于叠后地震数据的，忽略了部分地震信息。相比叠后反演，叠前反演具有较高的保真度，且能得到泊松比、拉梅参数以及孔隙度、泥质含量、含流体饱和度等多种参数，进而为储层预测提供更可靠的信息[23]。

叠前地震反演的理论基础是Zoeppritz方程，然而精确的Zoeppritz方程极其复杂，不利于反演[24]。因此，前人对其进行了简化，提出了Zoeppritz近似方程。Aki等[25]首次提出了Aki-Richards近似公式，本文基于该近似公式进行基于随机反演的叠前反演研究。

Aki-Richards近似公式具体形式为

(8)

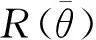
要利用量子退火MH算法进行叠前反演，需要构建后验概率表达形式，即目标函数。贝叶斯理论是其基础，它将先验信息通过似然函数转化为后验信息[26]，利用量子退火MH算法对后验概率密度进行抽样，便可获得后验概率的一系列样本。

本文所研究的反演问题可以表述为

p(vP,vS,ρ|d)=f(vP,vS,ρ)+e

(9)

式中：d为观测地震数据；f代表正演算子；e代表观测噪声。待反演参数vP、vS以及ρ的后验概率密度可写作

p(vP,vS,ρ|d)=p(vP,vS,ρ)·p(d|vP,vS,ρ)

(10)

对于似然函数，假设地震噪声满足均值为0、方差为σn的正态分布，则似然函数可表示为

(11)

式中N表示待反演参数的样本数量。

假设待反演参数vP、vS以及ρ均服从高斯分布，且相互独立，那么待反演参数的先验信息可表示为

p(vP,vS,ρ)=p(vP)·p(vS)·p(ρ)

(12)

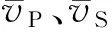
(13)

最后我们利用量子退火MH算法进行反演，最终得到收敛于后验概率密度分布的马尔科夫链，再对马尔科夫链进行统计分析，即可获得反演参数vP、vS及ρ。

3 模型测试

3.1 一维模型测试

首先利用一维模型进行反演测试，该一维模型来自实际井资料。子波选取25Hz的零相位雷克子波，设置炮检距为100～1000m。利用炮检距、速度、时间深度等参数通过计算得到角度信息，然后利用式(8)计算反射系数，与子波进行褶积，并加入一定噪声(SNR=3)，最终得到观测地震记录。

图2为传统MH算法反演结果与模型数据的对比，图3为在相同搜索策略下量子退火MH算法反演结果与模型数据的对比。可以发现当搜索策略相同时，量子退火MH算法反演结果要优于传统的MH算法反演。

图4为观测地震记录、未加噪声的地震记录及传统MH算法和量子退火MH算法反演结果合成的地震记录，由图可见，量子退火MH算法反演结果所合成的地震记录与实际地震记录更加接近。这是由于Γ的引入能够适当调整原有的接受概率，减少当前状态不必要的转移，使算法更加稳定地收敛于后验概率分布。

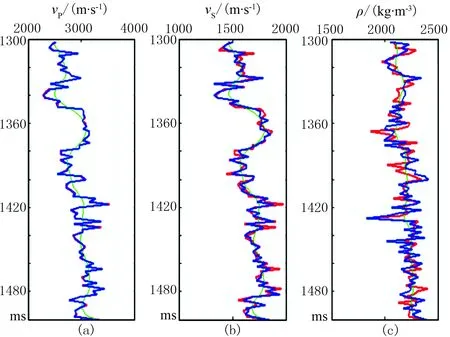
图2 传统MH算法反演结果与模型数据的对比 绿线为初始模型，红线为模型数据，蓝线为反演结果 (a)vP; (b)vS; (c)ρ

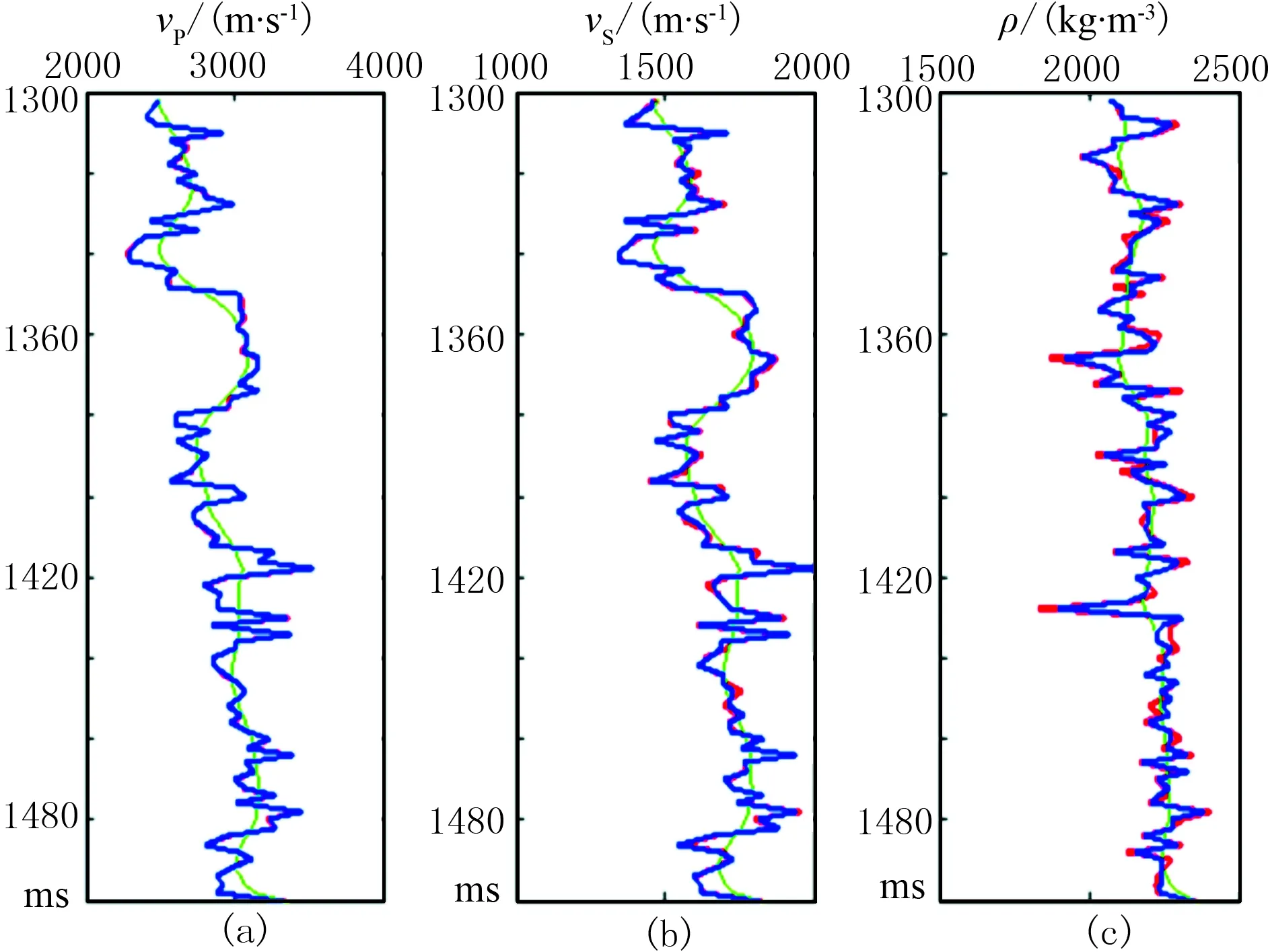
图3 量子退火MH算法反演结果与模型数据的对比 绿线为初始模型，红线为模型数据，蓝线为反演结果 (a)vP; (b)vS; (c)ρ

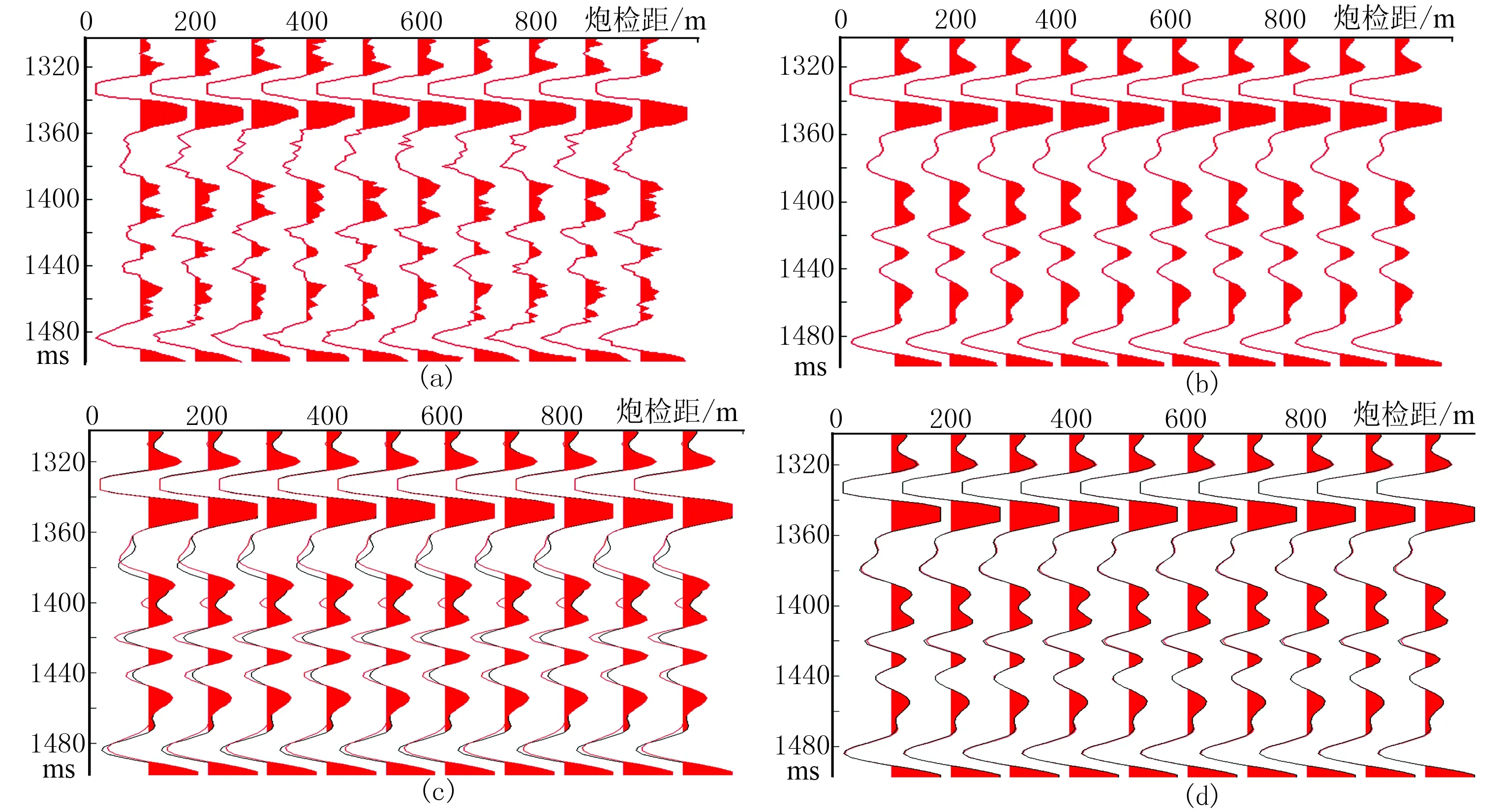
图4 观测地震记录(a)、未加噪声的地震记录(b)及传统MH算法(c)和量子退火MH算法(d)反演结果合成的地震记录 图c、图d中红线为反演结果合成的记录，黑线为未加噪声的合成记录

从一维模型中选取某一位置处的采样点，比较两种方法在该采样点处密度值的迭代结果的变化。图5为分别利用传统MH算法和量子退火MH算法在某采样点的纵波速度值随迭代次数的变化曲线。

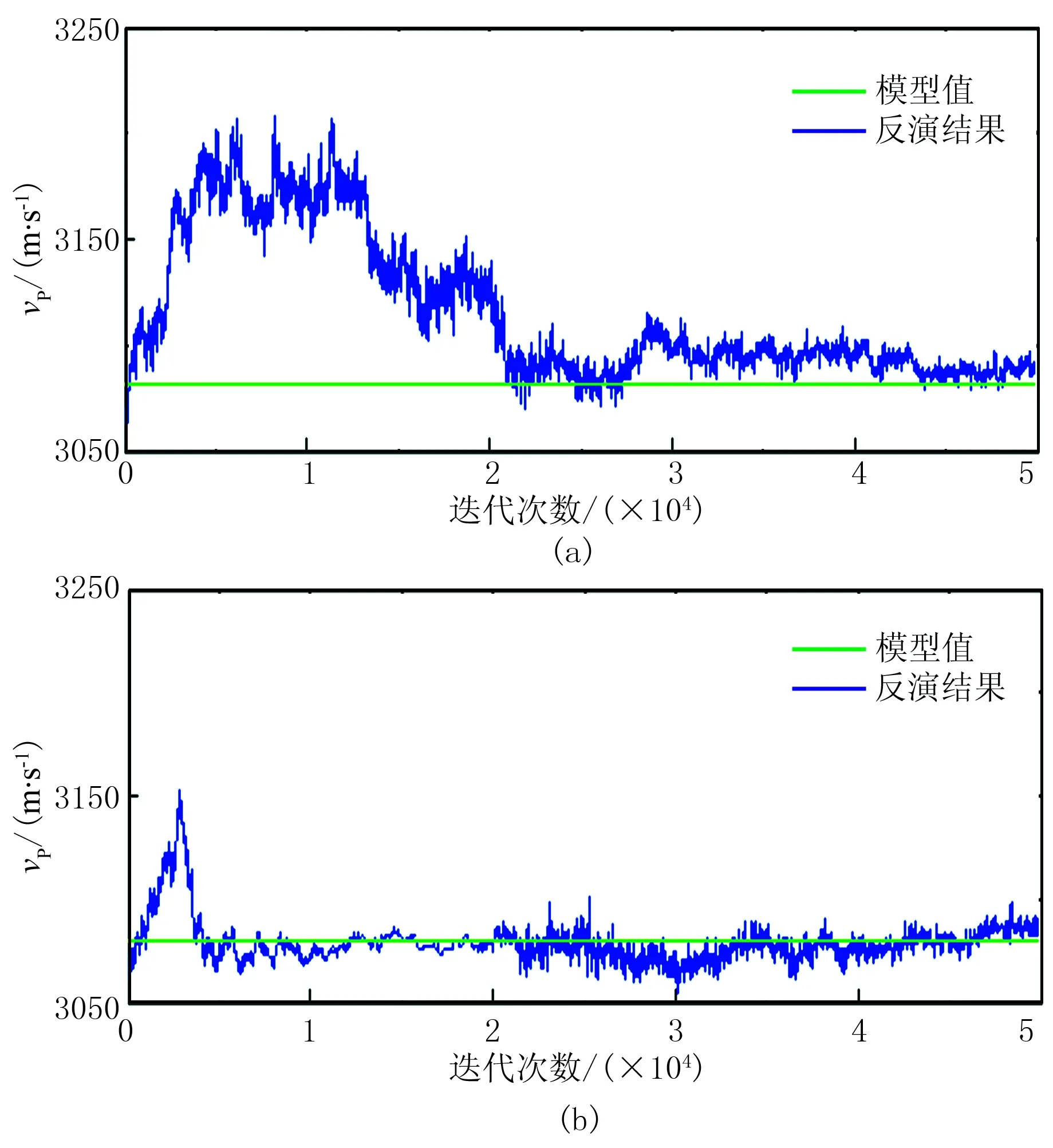
图5 分别利用传统MH算法(a)和量子退火MH 算法(b)的纵波速度值随迭代次数的变化

由图5可见，传统MH算法在迭代到20000次左右才开始在真值附近区域内采样，共耗时1230.1s，而量子退火MH算法在4000次左右就开始在真值

附近区域内采样，共耗时228.1s，且后者的稳定性要强于前者。这说明量子退火MH算法相比传统的MH算法具有更高的计算效率，且反演结果更加稳定。

利用量子退火MH算法进行叠前反演，可以同时获得同一个采样点的纵、横波速度以及密度的多个反演结果(图6)，进行概率统计与不确定性估算。由图可见，纵、横波速度与密度反演结果的概率统计均表现为高斯分布，这与给出的先验假设一致。

3.2 二维模型测试

为了进一步验证基于量子退火MH算法的随机反演方法的可行性，利用部分Marmous2二维模型进行反演测试，选取模型的时窗为1000～1600ms，地震子波选取频率为30Hz的雷克子波，设置炮检距为100～1000m。利用炮检距、速度、时间深度等参数计算入射角等信息，之后利用量子MH算法进行反演。

图7为反演结果(SNR=3)与模型数据的对比。由图可见，即使存在一定的噪声，反演结果与模型数据基本吻合,模型中的薄层也能很好地识别。

为了进一步说明反演结果的有效性，分别比较信噪比为1和3时，模型第61道的反演结果与模型数据(图8)。从图8可以发现，无论信噪比为1还是3，反演结果与模型数据均吻合较好，说明了该算法具有一定的抗噪能力。

图9为该二维模型某采样点纵波速度、横波速度和密度多个反演结果的概率直方图。由图可见，纵、横波速度与密度反演结果的概率统计均表现为高斯分布，这与先验假设一致。因此，可同样选择纵、横波速度和密度在某采样点处反演的均值作为最大后验概率估计。

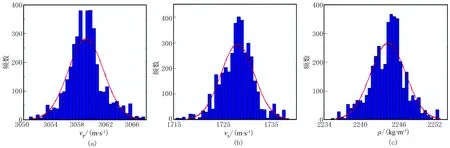
图6 某采样点的纵波速度vP(a)、横波速度vS(b)和密度ρ(c)的概率直方图

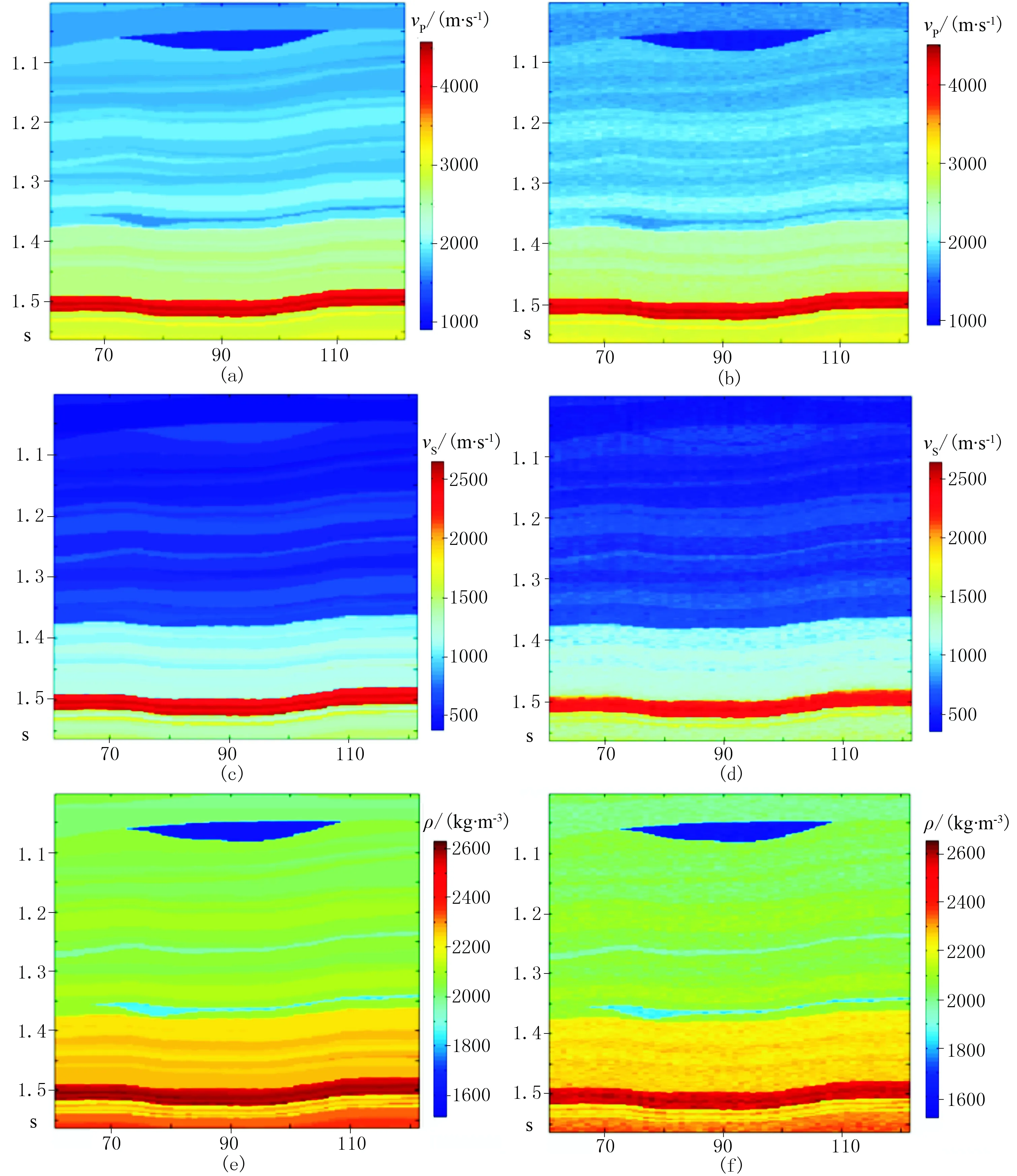
图7 反演结果与模型数据对比 (a)vP模型； (b)vP反演结果； (c)vS模型； (d)vS反演结果； (e)ρ模型； (f)ρ反演结果

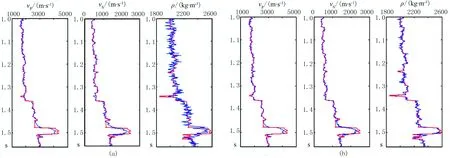
图8 vP、vS、ρ反演结果与模型数据对比 (a)SNR=1； (b)SNR=3

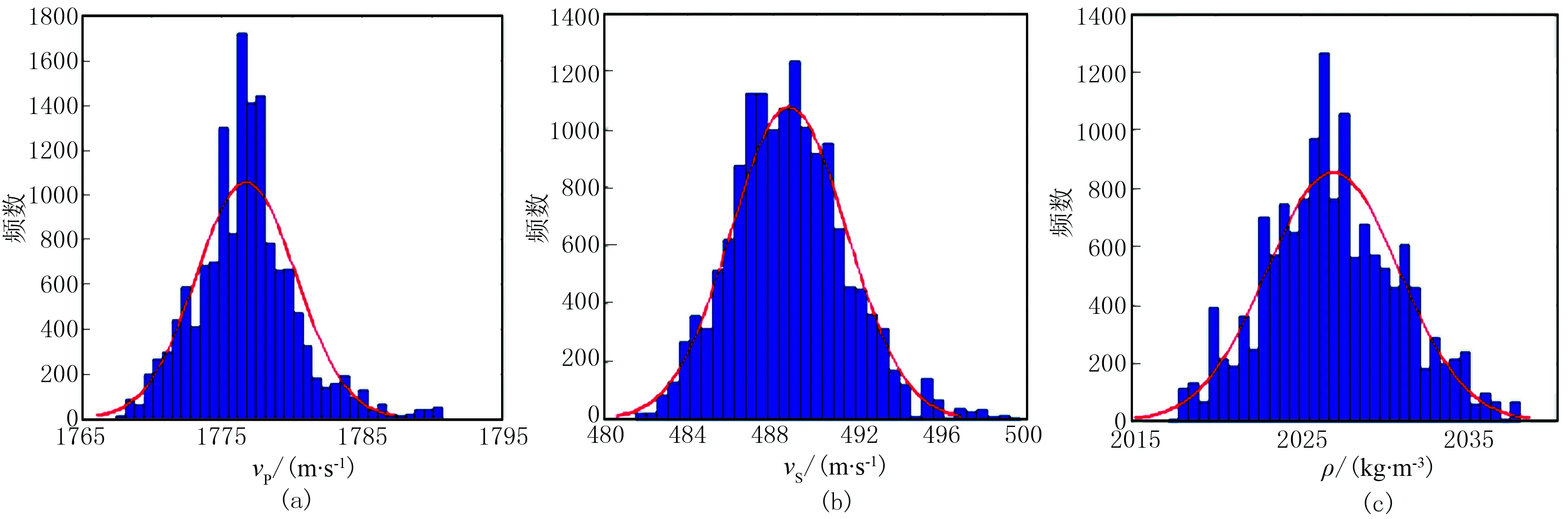
图9 某采样点纵波速度vP(a)、横波速度vS(b)和密度ρ(c)的概率直方图

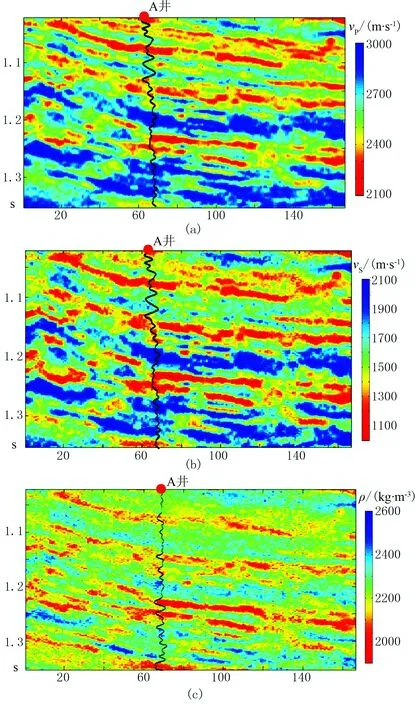
图10 纵波速度vP(a)、横波速度vS(b)和密度ρ(c)反演结果

4 实际资料分析

为了测试叠前随机反演方法在实际资料应用中的可行性，应用实际资料进行反演测试。该资料来自中国北部，最大入射角为35°左右，主要目标为多层系含油的典型复式油气聚集区，根据测井资料解释结果，密度可以很好地反映砂体分布。

为了提高反演的计算效率，将地震炮检距道集分为3°～13°、14°～24°、25°～35°三个角度部分叠加的地震剖面。为分析反演方法的效果，应用基于量子退火MH算法的叠前反演方法进行储层预测。

图10为反演结果。由图可见，反演结果与测井数据吻合较好，且密度反演结果能大体反映出砂体的分布特征，验证了该反演方法对实际数据进行反演的可行性。

5 结论

(1)借鉴量子退火的思路对MH算法进行改进，模型测试结果和实际数据的分析均表明，该反演方法能够获得纵、横波速度和密度参数，且收敛速度及稳定性相较于传统的MH算法有一定的提升；

(2)量子退火MH算法基于贝叶斯理论，将先验信息与似然函数相结合，提高了反演结果的稳定性，同时可获得收敛于后验概率分布的一系列样本，便于进行解的不确定分析；

(3)量子退火MH方法的核心在于φ的引入，它能够适当调整原有的接受概率，减少当前状态不必要的转移，使马尔科夫链能够更加快速稳定地收敛于后验概率密度，但是φ的选取原则及衰减函数还需进一步探索。

[1] 张繁昌,肖张波,印兴耀.地震数据约束下的贝叶斯随机反演.石油地球物理勘探,2014,49(1):176-182. Zhang Fanchang,Xiao Zhangbo,Yin Xingyao.Baye-sian stochastic inversion constrained by seismic data.OGP,2014,49(1):176-182.

[2] 李宁.基于模拟退火的地质统计学反演方法研究[学位论文].山东青岛：中国石油大学(华东),2013.

[3] 孙瑞莹.先验信息构建与地震随机反演方法研究[学位论文].山东青岛：中国石油大学(华东),2015.

[4] 王保丽,孙瑞莹,印兴耀等.基于Metropolis抽样的非线性反演方法.石油地球物理勘探,2015,50(1):111-117. Wang Baoli,Sun Ruiying,Yin Xingyao et al.Nonli-near inversion based on Metropolis sampling algorithm.OGP,2015,50(1):111-117.

[5] Metropolis N,Rosenbluth A,Rosenbluth M et a1.Equation of state calculations by fast computing machines.The Journal of Chemical Physics,1953,21(6):1087-1092．

[6] Hastings W K.Monte Carlo sampling methods using Markov chains and their applications. Biometrika,1970,57(1):97-109.

[7] Smith A F and Roberts G O.Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods.Journal of the Royal Statistical Society,1993,55(1):3-23.

[8] Alberto M，Carlos T V.Bayesian inversion of DC electrical measurements with uncertainties for reservoir monitoring.Inverse Problems,2000,16(5):1343-1356.

[9] Chen J S,Kemna A,Hubbard S S.A comparison between Gauss-Newton and Markov-chain Monte Carlo-based methods for inverting spectral induced-polarization data for Cole-Cole parameters.Geophysics,2008,73(6):F247-F259.

[10] 朱嵩,毛根海,刘国华等.改进的MCMC方法及其应用.水力学报,2009,40(8):1019-1023. Zhu Song,Mao Genhai,Liu Guohua et al.Improved MCMC method and its application.Journal of Hydraulic Engineering,2009,40(8):1019-1023.

[11] 张广智,王丹阳,印兴耀.利用MCMC方法估算地震参数.石油地球物理勘探,2011,46(4):605-609. Zhang Guangzhi,Wang Danyang and Yin Xingyao．Seismic parameter estimated using Markov Chain Monte Carlo method.OGP,2011,46(4):605-609.

[12] 李远,张广智.基于改进MCMC的地震参数反演方法.中国地球物理学会第二十九届年会,2013.

[13] Harrio H,Saksman E and Tamminen J.Adaptive proposal distributions for random walk Metropolis algorithm.Computational Statistics,1999,14(3):375-396.

[14] Harrio H,Saksman E and Tamminen J.An adaptive Metropolis algorithm.Bernoulli,2001,7(2):223-242.

[15] 张广智,潘新朋,孙昌路等.纵横波联合叠前自适应MCMC反演方法.石油地球物理勘探,2016,51(5):938-946. Zhang Guangzhi,Pan Xinpeng,Sun Changlu et al.PP- & PS-wave prestack nonlinear inversion based on adaptive MCMC algorithm.OGP,2016,51(5):938-946.

[16] Pan Xinpeng,Zhang Guangzhi.Zeroppritz-based non-linear AVO inversion using AMDR-MCMC method.SEG Technical Program Expanded Abstracts,2016,35:572-576.

[17] 魏超,朱培民,王家映.量子退火反演的原理和实现.地球物理学报,2006,49(2):577-583. Wei Chao,Zhu Peimin,Wang Jiaying.Quantum annealing inversion and its implementation.Chinese Journal of Geophysics,2006,49(2):577-583.

[18] Alulaiw B,Sen M K.Prestack seismic inversion by quantum annealing: application to Cana Field.SEG Technical Program Expanded Abstracts,2015,34:3507-3511.

[19] 李远.基于AM-MCMC的地震反演方法研究[学位论文].山东青岛：中国石油大学(华东),2014.

[20] 王丹阳.基于MCMC方法的叠前反演方法研究[学位论文].山东青岛：中国石油大学(华东),2012.

[21] 魏超,李小凡,张美根.量子退火最优化与地球物理反演方法.地球物理学进展,2007,22(3):785-789. Wei Chao,Li Xiaofan,Zhang Meigen.Quantum annealing optimization and geophysical inverse method.Progress in Geophysics,2007,22(3):785-789.

[22] 方中于,王丽萍,杜家元等.基于混合智能优化算法的非线性AVO反演.石油地球物理勘探,2017,52(4):797-804. Fang Zhongyu,Wang Liping,Du Jiayuan et al.Nonlinear AVO inversion based on hybrid intelligent optimization algorithm.OGP,2017,52(4):797-804.

[23] 李建华,刘百红,张延庆等.叠前AVO反演在储层含油气性预测中的应用.石油地球物理勘探,2016,51(6):1180-1186. Li Jianhua,Liu Baihong,Zhang Yanqing et al.Oil-bearing reservoir prediction with prestack AVO inversion.OGP,2016,51(6):1180-1186.

[24] 张璐.基于岩石物理的地震储层预测方法应用研究[学位论文].山东青岛：中国石油大学(华东),2009.

[25] Aki K,Richards P G.Quantitative Seismology: Theory and Methods.WH Freeman & Co,San Francisco，1980.

[26] V.Vapnik著;张学工译.统计学习理论的本质.北京:清华大学华夏出版社,2000.

[27] 潘新朋.优化MCMC方法在地震反演中的应用研究[学位论文].山东青岛：中国石油大学(华东),2016.