缸内直喷汽油机共轨系统结构参数优化

胡云峰, 王长勇, 于树友, 孙鹏远，陈 虹

(1. 吉林大学 汽车仿真与控制国家重点实验室，长春 130022；2. 吉林大学 通信工程学院，长春 130022；3. 中国第一汽车集团公司 技术中心，长春 130011)

0 前言

随着汽车产业的迅速发展，缸内直喷汽油机(GDI)共轨技术在汽车发动机领域得到了广泛的应用，GDI共轨系统能够保持高性能工作的前提是共轨系统具有稳定的共轨压力，不稳定的共轨压力将使喷油量无法精准控制，最终使发动机的性能变差[1]。GDI共轨系统中有诸多因素影响共轨压力的稳定，其中结构参数是影响共轨压力波动的关键因素，因此通过合理设计共轨系统结构参数，抑制共轨压力波动是一项有意义的工作[2]；此外，若直接使用共轨实物进行结构参数标定开发周期长，且成本非常高。

针对共轨系统结构参数对共轨系统特性的影响，文献[3]在GT-fuel中建立了高压泵的仿真模型，研究了高压泵进油阀组件、出油阀组件以及柱塞凸轮组件等结构参数对共轨压力的影响，并对比了不同高压泵结构参数对轨压波动的影响；文献[4]利用AMESim建立了电控单体泵燃油系统模型，通过对不同高压油管结构参数的燃油系统进行仿真研究,分析了高压油管长度、内径及内壁粗糙度对单体泵供油压力、喷油压力及循环喷油量等燃油系统性能参数的影响；文献[5]为研究喷油器喷嘴关键结构参数对喷雾的影响，采用数值模拟方法在保持喷孔总流通截面积相同的情况下，通过改变喷孔数目、喷孔直径、喷孔长度等结构、参数，分析了喷油器结构参数对喷雾特性的影响。目前针对共轨系统结构参数的研究仅限于采用商业软件对共轨内的压力波动进行模拟及仿真分析[6]，通过仿真实验给出设计共轨系统结构尺寸的大体准则，但对于最优结构尺寸的确定仍然主要是利用试凑法通过大量的仿真分析确定。这种方法的缺点是实验量大且不一定能够找到最优的结构参数，若利用优化算法取代盲目的试凑法对共轨系统结构参数进行优化，则能够在较小实验量、较短时间内得到结构参数的最优值，进而缩短了GDI共轨系统的开发周期。

遗传算法作为一种智能寻优算法，具有全局优化的优点，被广泛的应用于函数优化、汽车控制、机器人学、图像处理以及人工生命等领域[7-9]，但是其局部寻优能力较差，最终收敛到最优解往往花费较长的时间[10,11]。

本文为实现对GDI共轨系统结构参数的优化设计，首先在GT-suite中建立了GDI共轨系统的模型，并对该模型进行了动力学特性分析，确定将共轨管的体积以及阻尼孔直径作为优化变量，在进行结构参数优化时采用前馈加反馈的控制策略对共轨压力实现了实时控制。随后利用改进型遗传算法对阻尼孔直径以及共轨管体积进行多变量结构参数优化。最后通过对比优化前、后共轨系统性能验证了本文优化方法的有效性。

1 GDI共轨系统建模及动力学分析

1.1 GDI共轨系统建模

1.1.1 高压泵工作机理与建模

高压泵主要包括：进油口燃油计量阀，凸轮驱动的柱塞泵，以及出油阀及安全阀。进油口处燃油计量阀的主要作用的是控制进入高压泵的燃油量，从而实现对共轨压力的调节；出油阀是一个单向阀，主要由复位弹簧以及阀芯、阀座组成，安全阀处于高压泵出口处，当出口处压力大于预设安全压力时，安全阀开启；高压泵腔体的体积随着凸轮轴的转动变化而变化，结合其凸轮形线，泵腔体积可表示如下：

Vp(θ)=Vp0-APhp(θ)

(1)

式中：Vp(θ)为高压泵体积变化量，m3；Vp0为高压泵的初始体积，m3；Ap为高压泵柱塞横截面积，m2；hp(θ)为高压泵柱塞行程，m。

根据燃油体积弹性模量公式及流量公式，高压泵内的燃油压力Pp满足下式：

(2)

式中：Kf为燃油的弹性模量，105Pa；qu表示从低压泵进入的燃油流量；qpr为流入共轨管的燃油流量；q0为燃油泄漏流量，m3/t；pp为高压泵压强，pr为共轨管压强，105Pa；Apr为阻尼孔的横截面积，m2；cpr为液体流量系数;

(3)

(4)

根据以上高压泵结构，在GT-suite中搭建的高压泵模型如图1所示。

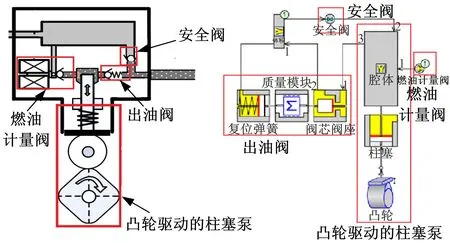
图1 高压泵结构及GT-suite模型Fig.1 Structure and GT-suite model of high-pressure pump

1.1.2 共轨管工作机理与建模

共轨管是共轨系统的主要部件，共轨管的作用是储存高压泵提供的高压燃油并分配到各喷油器中，同时缓冲由于高压泵供油以及喷油器喷油所产生的压力波动。共轨管在结构上主要包括连接高压泵端的阻尼孔，连接喷油器端的节流孔，以及轨压传感器，压力限制阀，若把共轨管体积看作常值，则共轨管内燃油压力变化满足如下关系式：

(5)

(6)

根据共轨管结构，在GT-suite中搭建的共轨管模型如图2所示。

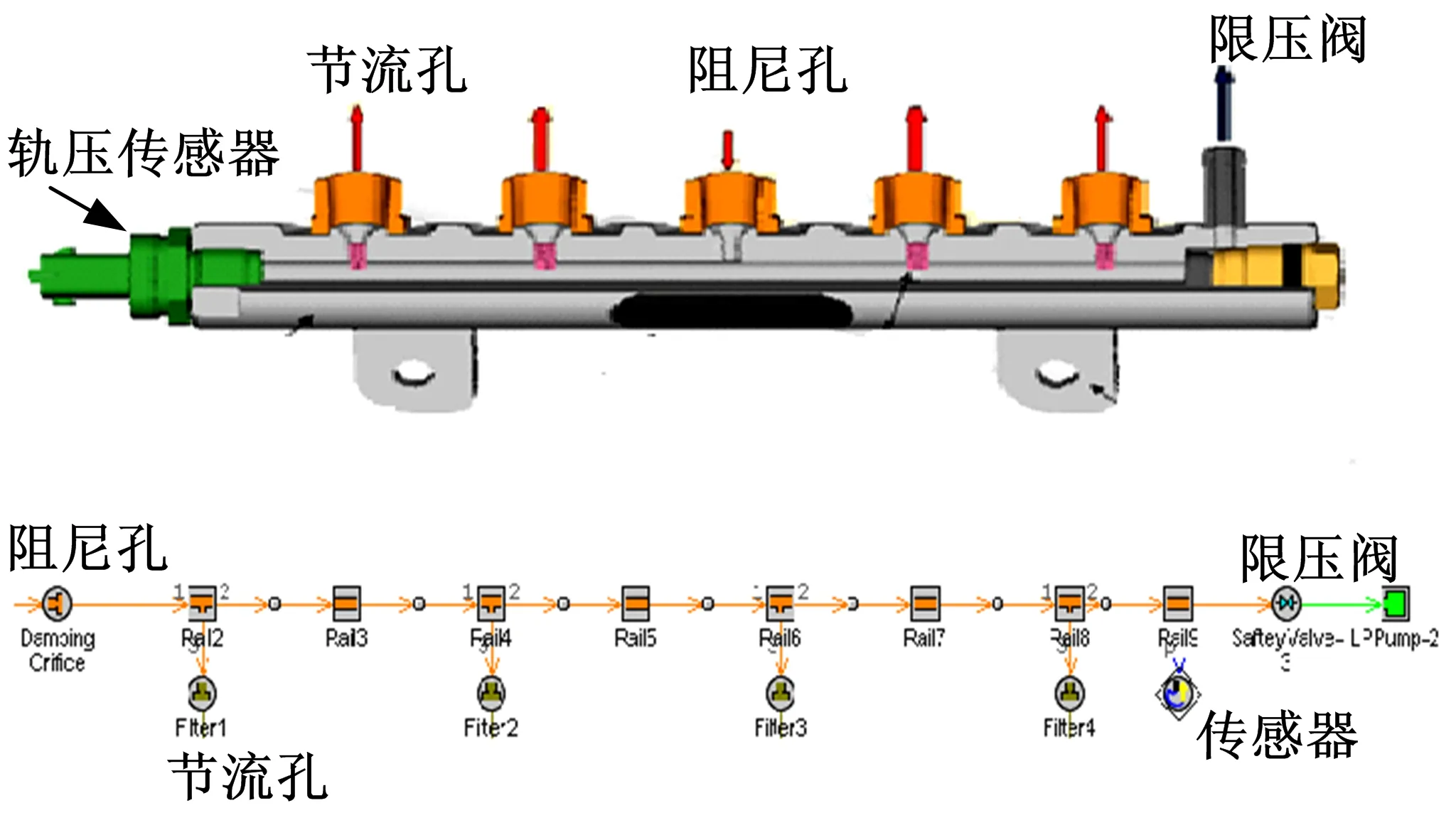
图2 共轨管结构及GT-suite模型Fig.2 Structure and GT-suite model of common rail pipe

1.1.3 喷油器工作机理与建模

喷油器主要由电磁阀、衔铁、针阀、复位弹簧，喷油器腔等组成，电磁阀由ECU信号控制，电磁阀的开关使得衔铁、针阀移动，最终实现喷油器喷油。根据弹性体积模量公式及流量公式，喷油器腔内压力微分方程为：

(7)

式中：qri,k、qinj,k分别为由共轨管进入喷油器，由喷油器进入气缸的燃油流量，m3/t；Vik为喷油腔体积，cm3；ETK为喷油正时信号；pcyl,k为气缸压强,105Pa;pik为喷油器压强,105Pa;

qinj,k=sgn(pik-pcyl,k)cikETKAik

(8)

根据喷油器的物理结构在GT-suite中建立喷油器模型,如图3所示。

图3 喷油器结构及GT-suite模型Fig.3 Structure and GT-suite model of injector

为了完善整个GDI共轨燃油喷射系统，本文对低压油路进行简化建模，将其简化成一个以恒定压力(4×105Pa)泵油的低压泵，基于GT-suite所建立的GDI共轨系统如图4所示。

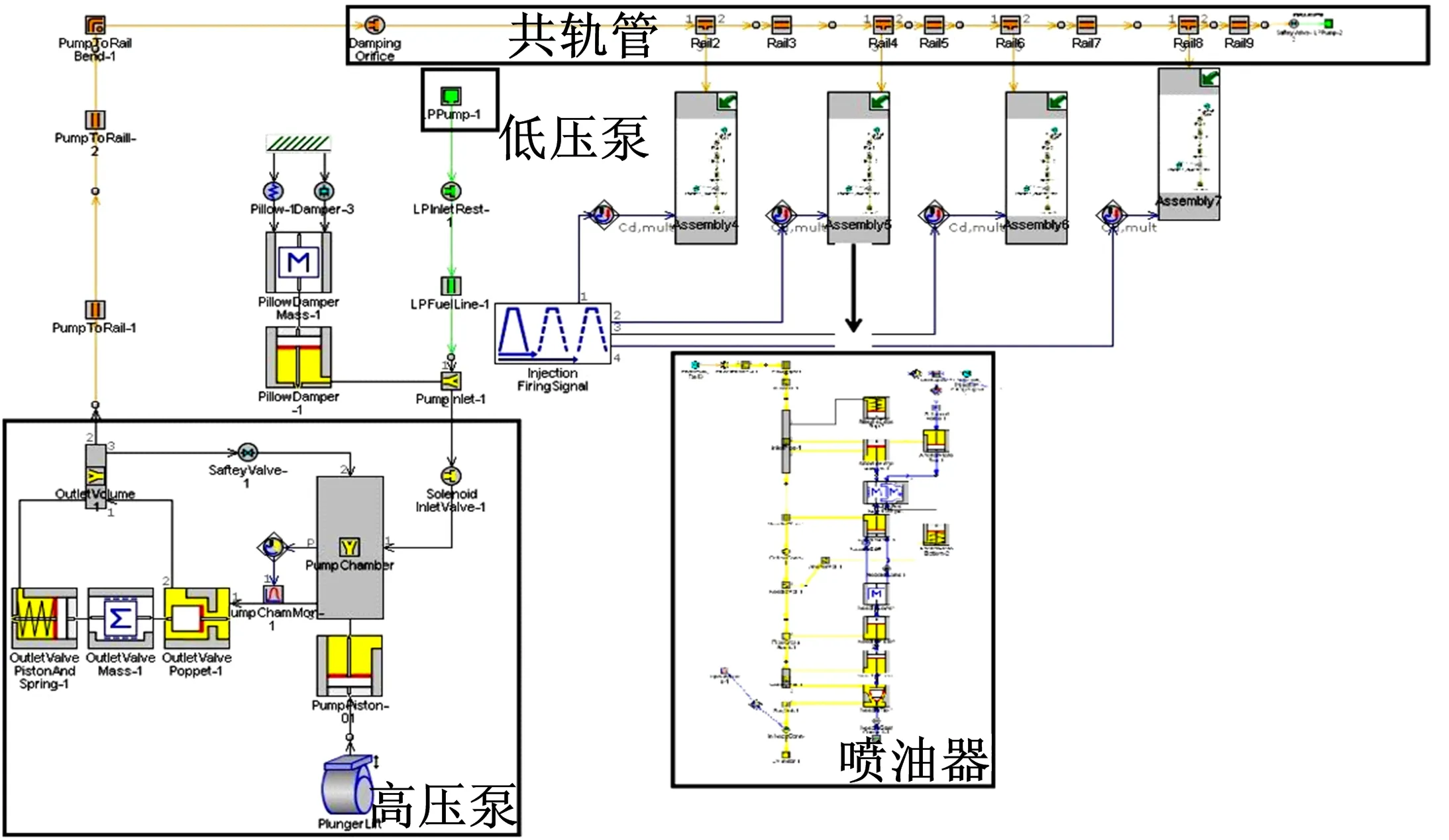
图4 基于GT-suite的GDI共轨系统模型Fig.4 GT-model of GDI common rail system

本文以GT-suite软件供应商所提供的GDI共轨系统参数为所建立的GDI共轨系统模型匹配参数，部分参数如下：阻尼孔直径为1 mm;共轨管直径(内)为8 mm；共轨管长度为240 mm；共轨管进出油孔数为5；发动机转速为2500 r/min;期望轨压为1.5×107Pa;初始轨压为1.4×107Pa。利用所搭建的GDI共轨系统模型与台架数据进行对比，如表1所示,模型的总体误差在5%内，满足精度要求。

表1 GT-suite模型与台架实验结果对比Table1 Comparison of results between GT-suite and bench

1.2 GDI共轨系统动力学特性分析

1.2.1 论分析

1.2.2 实验分析

1.1节利用GDI共轨系统数学模型从理论上分析了共轨管体积以及阻尼孔直径对轨压波动的影响，但由于该数学模型未涉及共轨压力的上升时间，因此只利用数学模型无法分析共轨系统的结构参数对上升时间的影响，为了进一步研究GDI共轨系统结构参数对共轨压力上升时间的影响，接下来利用GDI共轨系统仿真模型对共轨管体积以及阻尼孔直径进行分析。此外，为说明其他结构参数对轨压波动的影响，改变高压泵体积以及喷油器进油孔直径进行实验分析，分别选取阻尼孔直径为0.75、1.0、1.5 mm；共轨管体积为6.785、12.063、18.850 cm3；高压泵体积为1.8、2.5、3.3 cm3；喷油器进油孔直径为0.69、0.89、1.2 mm。设定期望共轨压力1.5×107Pa，初始轨压1.4×107Pa，发动机转速2500 r/min进行实验，得到不同结构参数下的共轨压力波动及上升时间，如表2所示。

表2 不同结构参数下共轨压力波动及上升时间Table2 Pressure fluctuation and rise time of different structure parameters

由表2可知，相较于高压泵体积与喷油器进油孔直径，阻尼孔直径和共轨管体积对共轨系统轨压波动以及上升时间影响更明显。

图5、图6更清楚地反映了阻尼孔直径和共轨管体积对轨压波动以及上升时间的影响。如图5所示，随着阻尼孔直径的增大，轨压波动越来越大，而上升时间越来越短。

图5不同阻尼孔直径下的共轨压力波动及上升时间

Fig.5Pressurefluctuationandrisetimeofdifferentdampingholediameters

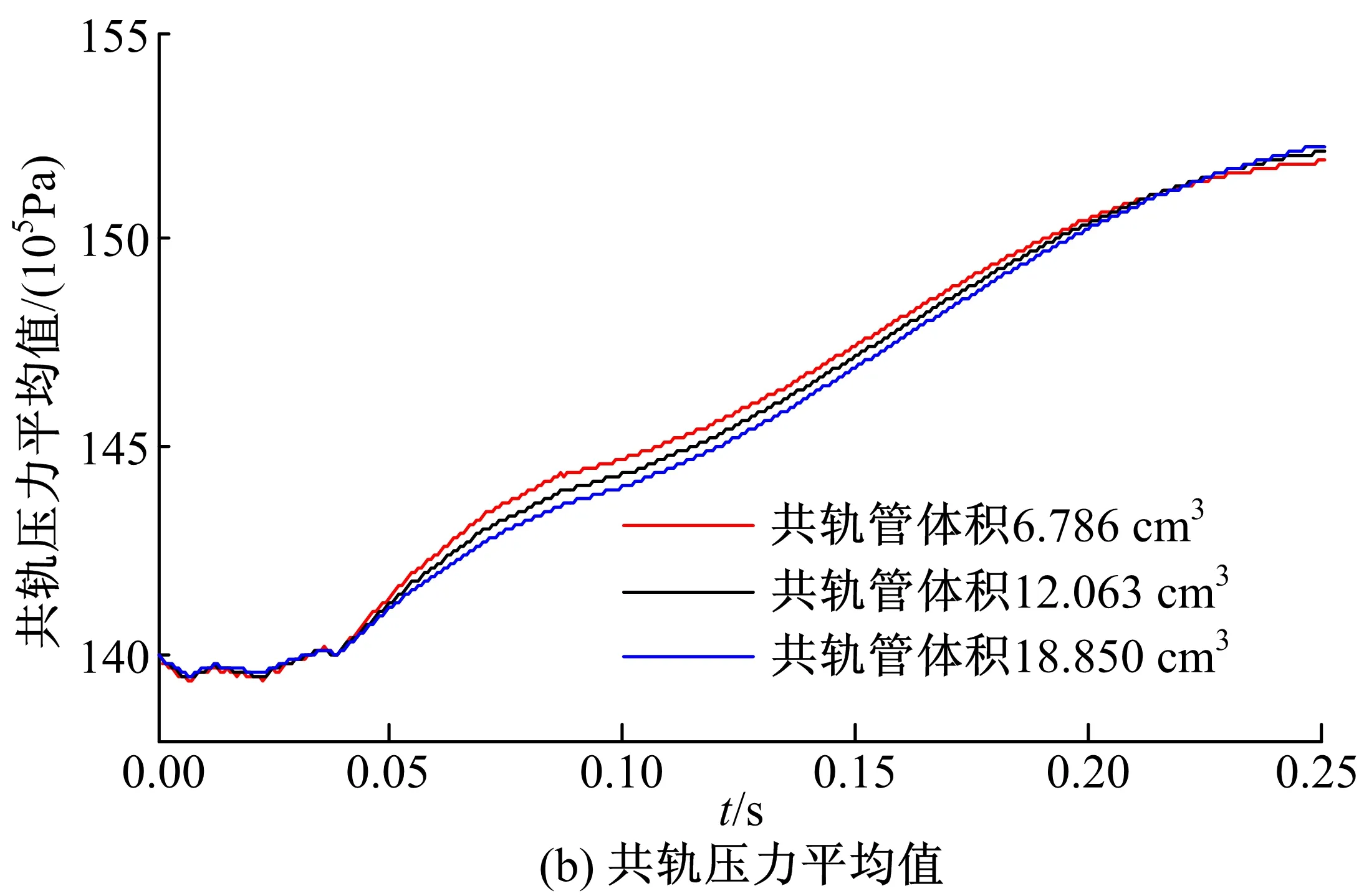
图6 不同共轨管体积下的共轨压力波动及上升时间Fig.6 Pressure fluctuation and rise time of differentcommon rail pipe volumes

由图6可知，随着共轨管体积的增大，轨压波动越来越小，而上升时间越来越长, 这与之前理论分析的结果一致，进一步验证了本文的GDI共轨系统GT-suite模型能够合理地反映GDI共轨系统的特性。

2 基于改进型遗传算法的共轨系统结构参数优化

2.1 共轨压力控制系统设计及有效性验证

GDI共轨系统的结构参数优化需要在闭环控制系统下进行，为了保证GDI共轨系统共轨压力在各个工作点能够稳定地跟踪上期望值，本文采用前馈控制和反馈相结合的控制策略设计轨压控制系统。

对于GDI共轨压力的控制，主要是通过控制GDI共轨系统高压泵前端的燃油计量阀开断实现的，因此控制系统前馈部分标定了一张关于高压泵前端燃油计量阀开度的map表，如图7所示， map表的输入为当前共轨压力以及喷油器的喷油量，输出为高压泵一个泵油工作周期内燃油计量阀的开度。对于该map的标定，给定GDI共轨系统GT-suite模型不同的燃油计量阀开度[5，10，…，120]， 记录下稳态时的共轨压力以及每循环喷油质量。

控制系统的反馈部分选用的传统的增量型PID控制器。其控制率表达形式为：

(9)

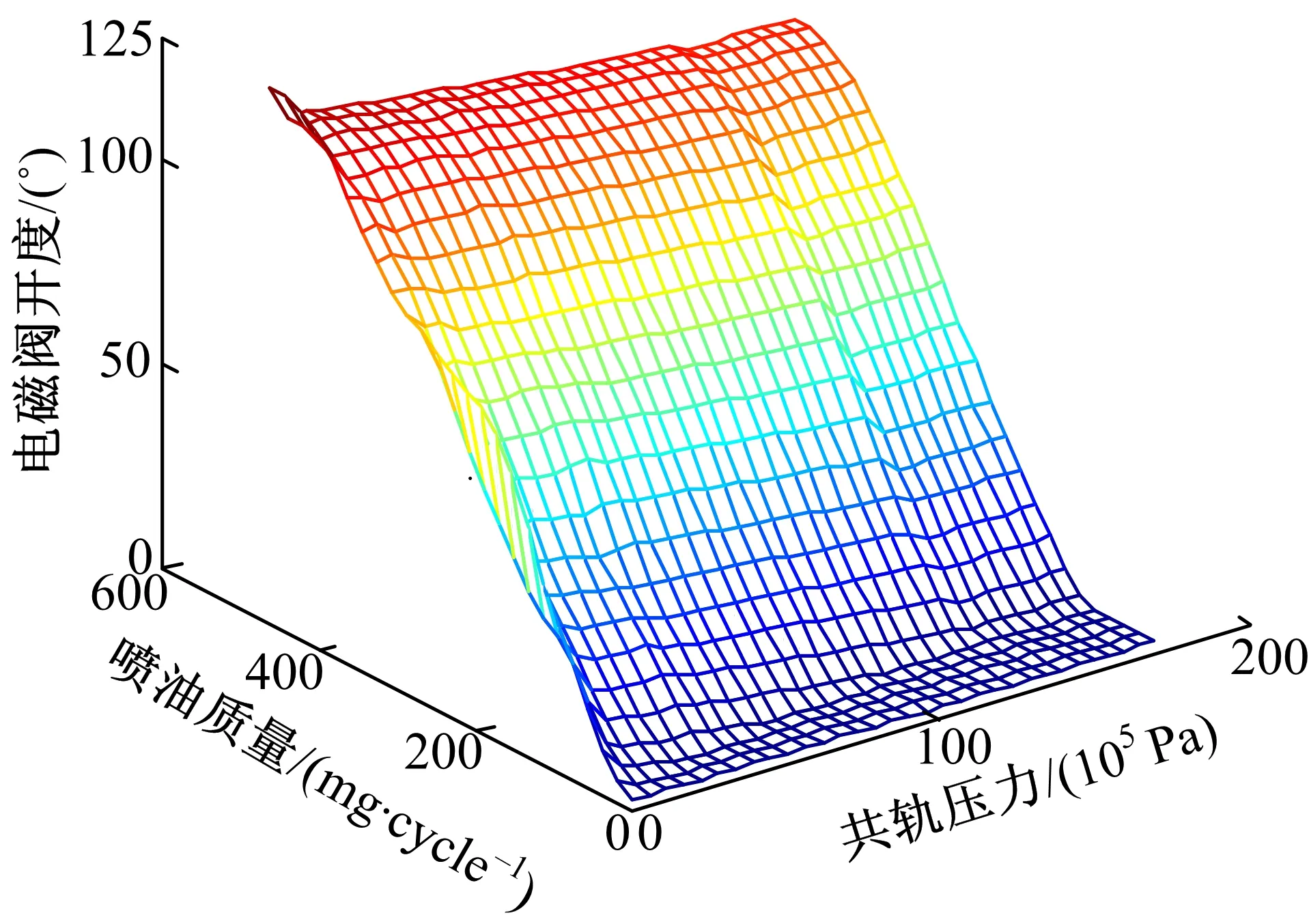
图7 电磁阀开度mapFig.7 Map of solenoid valve

整个GDI共轨系统的轨压控制框图如图8所示。

图8 GDI共轨压力控制框图Fig.8 Control structure of GDI common rail pressure

接下来进行控制系统的有效性验证，选取期望轨压分别为常值，连续阶跃信号以及正弦信号进行实验，实验结果如图9所示。

由图9可知，实际共轨压力较好地跟踪上期望轨压且轨压波动小于5×105Pa，证明了所设计的共轨压力控制系统的有效性。

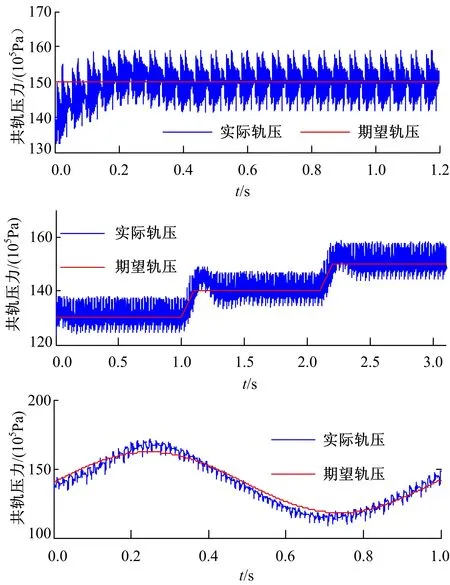
图9 共轨压力跟踪曲线Fig.9 Track curve of common pressure

2.2 共轨系统结构参数优化方法设计

在保证控制系统能够使共轨压力在各工作点稳定跟踪上期望轨压的基础上，为降低共轨压力波动，加快轨压的响应时间，接下来将利用优化算法对高压共轨系统结构参数进行优化。

遗传算法作为一种全局搜索方法，具有较强的全局搜索能力强，但遗传算法局部搜索能力较弱导致搜索最优解的时间较长且不易找到最优解。针对这一缺点，本文提出了一种标准遗传算法和序列二次规划算法相结合的改进型遗传算法，该改进型遗传算法，首先采用遗传算法进行全局搜索，当遗传算法寻优代数达到10n(n=1,2,…)时以遗传算法当前迭代得到的最优值作为序列二次规划算法fmincon的初值进行局部搜索，并把局部寻优得到的最优值替换原来遗传算法的最优值继续进行遗传算法迭代。

基于改进型遗传算法的GDI共轨系统控制及结构参数优化框图如图10所示。

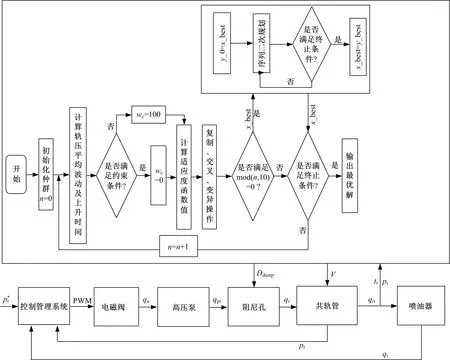
图10 基于改进型遗传算法共轨系统结构参数优化框图Fig.10 Diagram of structural parameters optimization of common rail system

2.2.1 适应度函数及优化变量的选取

对于适应度函数的选取，主要从改善喷油质量、提升发动机性能的角度考虑，要求GDI共轨系统轨压波动尽可能小，即：

(10)

式中：pi代表第i时刻的共轨压力；pr代表期望的共轨压力；N表示总的采样点个数。

为了适应不同的发动机工况需求，共轨压力的建立时间应尽可能小，即:

Minf2(tr)=tr

(11)

式中：tr表示上升时间。

因此本文中的共轨系统结构参数优化问题是一个多目标优化问题，对于该多目标优化问题，本文利用加权思想将多目标优化变成单目标优化，因此适应度函数为：

Minf(pi,tr)=k1f1(pi)+k2f2(tr)

(12)

式中：k1、k2表示共轨压力波动及上升时间的加权因子，考虑到轨压波动的数值范围为是(1,10)而上升时间的数值范围为(0.16,0.25) ，且本次优化更看重的是降低轨压波动这一优化目标，因此选取k1=1,k2=10。

优化变量的选取是优化算法的基础，是设计最后所需确定的参数，通过对共轨系统动力学的分析，本文选取共轨管体积Vr以及阻尼孔直径Ddamp作为优化变量。

2.2.2 约束条件的选取

为保证共轨系统的安全以及共轨系统结构的合理性，必须根据实际的共轨系统对流体流动，共轨管体积，阻尼孔直径等进行约束，约束条件如表3所示。对于几何约束条件，在变量赋值时可以进行变量范围的约束，对于目标约束条件，采用惩罚函数策略，将约束条件转化成目标函数中的惩罚项，从而将一个有约束的优化问题转化成无约束的优化问题，对于最小化的非线性问题，通常采用加法形式构造目标函数, 惩罚项由惩罚因子和对违反约束的惩罚构成，因此适应度函数(11)最终的表达形式为：

Minf(pi,tr)=(1+wc)·(k1f1(pi)+k2f2(tr))

(13)

式中：wc为惩罚因子，当共轨压力的平均波动小于5×105Pa，且上升时间小于0.2 s时，wc=0;否则wc=100。

表3 约束条件的选取Table 4 Selection of constraints

2.2.3 共轨系统结构参数优化结果及分析

GDI共轨系统各个结构相互耦合是共轨系统的一个特点，目前国内对共轨系统结构的优化研究大多数集中于对单个结构参数进行优化，未考虑各结构间对共轨压力的耦合效应。本文考虑到共轨管体积和阻尼孔直径对共轨系统轨压的影响存在耦合关系，因此，对阻尼孔直径以及共轨管体积进行多变量结构参数优化。相比于单变量的遗传算法，多变量的遗传算法有以下不同：

(1)变量维数。变量维数由1维变成2维，考虑到变量之间的相互影响，此时的种群规模及种群代数应适当增大。

(2)编码方式。之前的单变量优化采用的是二进制编码，随着变量个数的增加，二进制编码会导致算法速度减慢，因此多变量优化采用了实数编码的方式。

具体的改进型遗传算法参数设置如下：变量个数为2；种群规模为20；代数为20；精英个体为2；交叉概率为0.9；变异概率为0.1；变量范围为0.1～2 mm，3～20 cm2。

基于改进型遗传算法的GDI共轨系统结构参数优化实验结果如图11所示。

通过图11(a)可以看出：随着种群代数的增加，每代种群适应度函数的最小值和平均值逐渐减小，前4组平均数值大，是由于此时的共轨管体积与阻尼孔直径选取不合理导致轨压波动或上升时间不满足约束条件造成的；图11(b)更好地显示了6代以后种群收敛过程；图11(c)代表每代种群各个变量间的平均距离；图11(d)给出了最终的优化结果：阻尼孔直径为0.9083 mm，共轨管体积为18.5812 cm3。

图12给出了阻尼孔直径以及共轨管体积优化前后的对比结果。优化后共轨系统的轨压波动变小，上升时间有所增加，这是因为本文在轨压波动及上升时间这两个优化指标中更看重轨压波动这一指标，因此在目标函数中轨压波动占比更大一些，若想加大上升时间的比重可以适当地调节权值k1、k2。

图11共轨管体积及阻尼孔直径优化结果
Fig.11Optimizationresultsofcommonrailpipevolumeanddampingholediameter

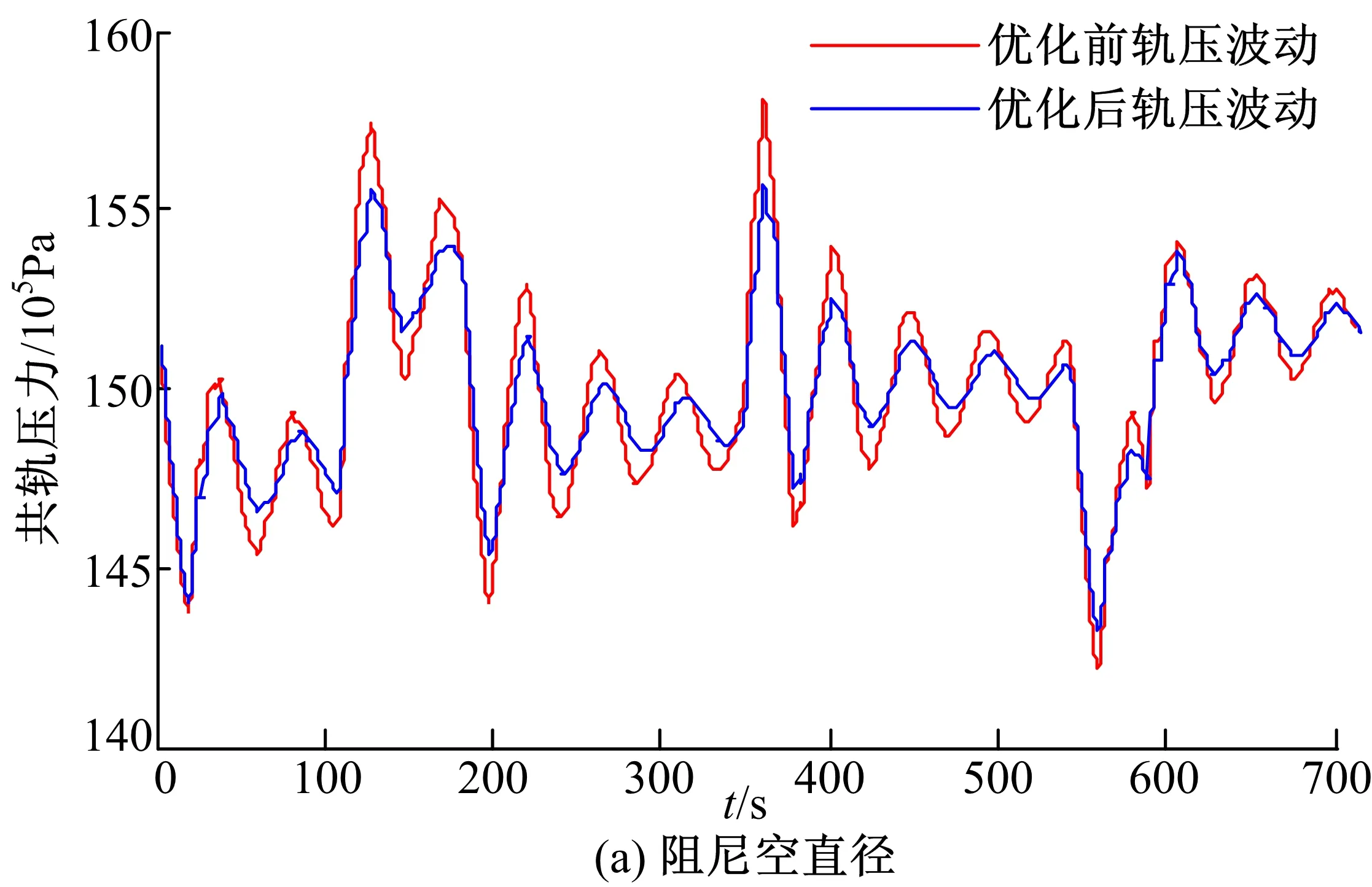
图12共轨系统结构参数优化前后结果对比
Fig.12Comparisonofresultsbetweenbeforeandafteroptimization

通过表4可以更清晰地看出，优化后的阻尼孔直径由1 mm变为0.9083 mm，共轨管体积由12.036 cm3变为18.5812 cm3，共轨压力波动由2.7494×105Pa优化至1.9338×105Pa，减少了29.7%。

表4 阻尼孔与共轨管多变量优化前后结果Table 4 Optimization results of common rail pipevolume and damping hole diameter

因此，在进行GDI共轨系统结构参数设计时，考虑各结构间的耦合效应, 进行多结构参数优化能够有效降低共轨压力波动，提升GDI共轨系统的性能。

4 结束语

本文为实现对GDI共轨系统的结构参数优化，搭建了GDI共轨系统的数学及仿真模型，设计了基于前馈和反馈的轨压控制系统，在此基础上，提出了标准遗传算法与序列二次规划算法相结合的改进型遗传算法，进而实现了对共轨系统结构参数的优化，优化后阻尼孔直径由1 mm变为0.9083 mm，共轨管体积由12.036 cm3变为18.5812 cm3，共轨压力波动由2.7494×105Pa减少至1.9338×105Pa，减少了29.7%，有效降低了共轨系统轨压波动。为GDI共轨系统结构参数的优化设计提供了一种新的思路。此外，考虑到共轨系统参数优化过程中存在约束，因此采用模型预测控制(MPC)做控制系统与共轨系统结构参数协同设计是可行的，这也将是作者后续将要开展的研究内容。

[1] Yan F J, Wang J M. Common rail injection system iterative learning control based parameter calibration for accurate fuel injection quantity control [J]. International Journal of Automotive Technology, 2011, 12(2): 149-157.

[2] Luo Z L, Huang K. Optimized design of structure parameter of new fuel injection system [J]. Advanced Materials Research, 2013, 655: 486-490.

[3] 张斌. 高压共轨系统高压泵结构参数对轨压波动影响的仿真研究[D]. 长春：吉林大学汽车工程学院, 2012.

Zhang Bin. Research on simulation of effects of high pressure pump structural parameters on the fluctuation of rail pressure[D]. Changchun: College of Automotive Engineering, Jilin University, 2012.

[4] 吕晓辰, 李国岫, 孙作宇, 等. 高压油管结构对电控单体泵燃油系统性能的影响[J]. 兵工学报, 2016, 37(10):1778-1787.

Lv Xiao-chen，Li Guo-xiu，Sun Zuo-yu，et al. Effect of high pressure fuel pipe structure on performance of electronic unit pump fuel system [J]. Acta Armamentarii, 2016, 37(10):1778-1787.

[5] 袁亚飞, 李丽, 宋睿智, 等. GDI喷油器喷嘴结构参数对喷雾特性影响分析[J]. 现代车用动力, 2016(3):22-27.

Yuan Ya-fei, Li Li, Song Rui-zhi, et al. Analysis of influence of key structure parameters about spray characteristic of injector in gasoline direct injection system [J]. Modern Vehicle Power, 2016(3):22-27.

[6] 裴海灵, 周乃君, 杨南, 等. 基于多学科设计优化的共轨管设计优化[J]. 中南大学学报：自然科学版, 2011, 42(1):234-239.

Pei Hai-ling, Zhou Nai-jun, Yang Nan, et al. Rail tube optimization based on multidisciplinary design optimization [J]. Journal of Central South University (Science and Technology)，2011, 42(1):234-239.

[7] 葛继科, 邱玉辉, 吴春明, 等. 遗传算法研究综述[J]. 计算机应用研究, 2008, 25(10):2911-2916.

Ge Ji-ke, Qiu Yu-hui, Wu Chun-ming, et al. Summary of genetic algorithms research [J]. Application Research of Computers, 2008, 25(10):2911-2916.

[8] 赵万忠, 施国标, 林逸, 等. 基于遗传算法的EPS系统参数优化[J]. 吉林大学学报:工学版, 2009, 39(2):286-290.

Zhao Wan-zhong, Shi Guo-biao, Lin Yi, et al. Parameter optimization of EPS system based on genetic algorithm [J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(2):286-290.

[9] 董立岩, 苑森淼, 刘光远, 等. 一种基于遗传算法的受限制的分类器学习算法[J]. 吉林大学学报:工学版, 2007, 37(3):595-599.

Dong Li-yan, Yuan Sen-miao, Liu Guang-yuan, et al. Constrained classifier learning algorithm based on genetic algorithm [J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(3):595-599.

[10] Li H,Zuo H, Liang K, et al. Optimizing combination of aircraft maintenance tasks by adaptive genetic algorithm based on cluster search [J]. Journal of Systems Engineering and Electronics, 2016, 27(1): 140-156.

[11] Wei X K, Shao W, Zhang C, et al. Improved self-adaptive genetic algorithm with quantum scheme for electromagnetic optimization [J]. IET Microwaves, Antennas & Propagation, 2014, 8(12): 965-972.