基于小波包变换和量子神经网络的触电故障类型识别模型

关海鸥，刘 梦，李春兰，杜松怀，李伟凯※

0 引 言

目前低压电网中广泛应用剩余电流保护装置，通常是将检测到的剩余电流大小作为发生触电故障的动作依据[1-3]，为避免其误动或拒动现象的发生，国内外学者进行了大量研究和改进[5-7]，文献[8-11]利用多种信号处理方法，研究了生物体触电支路电流幅值的计算方法，但未涉及到触电故障类型的识别方法。因此提取生物体触电故障时，剩余电流信号中时频数字特征，并正确识别触电故障类型，是发现剩余电流保护装置问题并进行治理和改善的重要前提条件。文献[12]利用剩余电流固有模态分量特征，实现了生物体发生触电故障的检测模型，但尚未解决通过经验模态分解提取各分量时，其分量数量及耗时在理论上具有不确定性的难题。小波包变换[13]能够在多层次分辨基础上，进行数字信号的特征分析，并在电力系统检测中得到成功应用。刘子洋等[14]利用小波包变换对含噪声的暂态电能质量扰动进行有效的检测与定位，分析了暂态电能质量。Vatansever Fahri等[15]通过希尔伯特变换后电流信号和原始电流与电压信号进行小波包变换和运算，实现了基波和各次谐波信号的功率计算。卢继平等[16]将小波包分解和信息熵相结合，研究了故障点两侧暂态零序电流波形差异较大和不同频率下的能量分布不同的问题。生物体发生触电故障时所检测的剩余电流，既含有高频信息，又含有低频信息。可利用小波包变换算法具有多分辨率分析的特点[17]，固定剩余电流分解层数，提取其暂态时频数字特征，为生物体触电故障类型识别模型提供有效的判断依据。人工神经网络具有较强的输入与输出映射功能和复杂的非线性处理能力，已普遍应用于电力系统故障模式分类。早在1989年文献[18]将电力系统的报警信息作为输入向量，建立基于BP神经网络的故障识别模型；吴欣等[19]利用贝叶斯网络实现了在不确定性和不完备信息下的电力系统故障诊断；文献[20‒21]将粗糙集理论与神经网络相结合，实现了电网故障模式分类方法；文献[22‒23]通过小波包提取电力系统故障的能量特征，实现了基于多小波包和人工神经网络的电力系统故障类型检测。上述研究成果未实现低压弱信号的剩余电流在识别生物体触电故障类型的应用，但为发挥神经网络和小波包变换各自优势，用以实现生物体触电故障类型与剩余电流之间的映射关系提供了基础，以解决剩余电流保护技术中及时准确识别触电故障类型的问题。本文应用小波包变换方法明确剩余电流中暂态时频数字特征，提取小波包能量特征向量为有效信息源，利用自适应量子神经网络的推理机制，建立基于小波包变换和量子神经网络的触电故障类型识别模型。同时应用多个量子能量级的量子神经元模型，构造前馈神经网络的激励函数，实现自适应地确定剩余电流与触电故障类型之间的非线性映射关系，简单直接地完成定性与定量之间的相互转换，以期提高触电故障类型识别效率。

1 基于小波包变换提取触电信号能量特征

1.1 小波包变换分解与重构

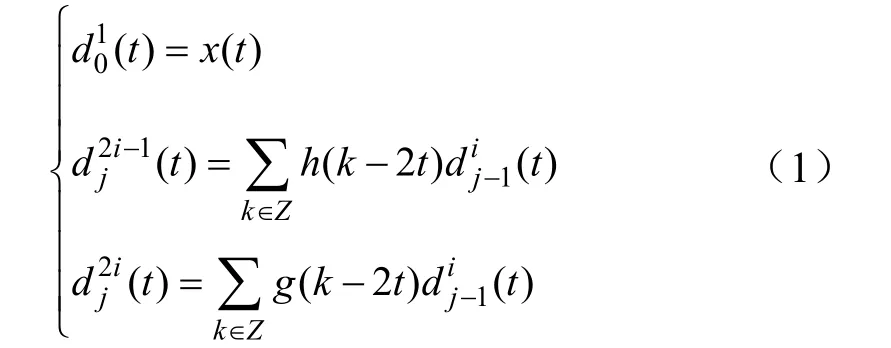
式中 j为分解层数，i=0,1,···,2j-1为频带节点，t=1,2, ···,n，n 为离散采样点数，k为平移因子，h(k)为低频滤波器，g(k)=(-1)kh(1-k)为高频滤波器，二者具有正交性。

应用小波包变换分解与重构方法，分析生物体触电信号，提取剩余电流的数字特征。

1.2 小波包能量特性分析过程

由于触电信号的时频特性分析中小波包变换是一种线性变换，满足能量守恒定理[25]

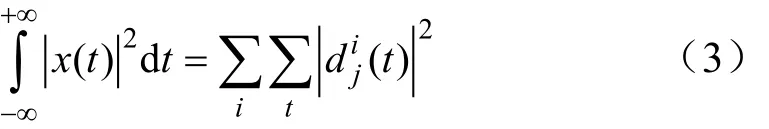
则第j层的第i个频带能量归一化处理可表示为

将第j层各频带能量谱归一化处理，可构成该层能量谱特征向量Vj为

生物体发生触电故障时剩余电流包含基波和不同的频率成分，考虑低压电网工频信号为50 Hz，采样频率为10 000 Hz，因此将剩余电流进行8层分解时，其频带节点个数为28，即剩余电流分解为256个频段，每个频带宽度为10 000/256 Hz，即39.0 625 Hz。

1.3 小波包能量特征分析实例

为保证小波包分解的相对稳定性和剩余电流保护技术的时效性，采用课题组设计的剩余电流动作保护装置触电物理试验系统平台，试验原理详见文献[5]。通过故障录波器获得生物体触电故障过程中剩余电流（图1a）、触电电流（图1b）、电源电压（图1c）的原始数据。截取工频15个周期的信号波形，其中包括触电前5个周期，触电后10个周期，相关电气信号的波形如图1所示。

图1 生物触电试验数据Fig.1 Experimental data of biological electrocution

图1 中横坐标为离散采样点（时间），共15个周期（3 000个点）；纵坐标对应采样时刻的电气回路相关电压和电流的有效值。其中电流值为实际真实值 2倍，为研究生物体触电故障类型识别模型提供原始数据。文中以哈尔正交小波函数对信号进行8层小波包分解与重构系数。该函数是在小波分析中最常用到的一个具有紧支撑的正交小波函数，其定义[28]为

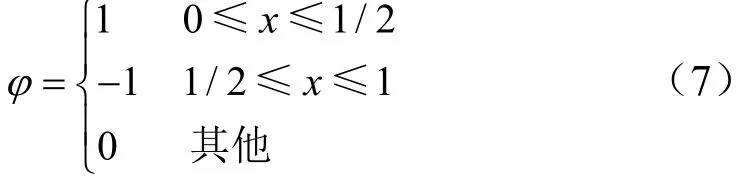
式中x为输入电流。

尺度函数为

哈尔正交小波函数的支撑长度为1，滤波器长度为2。应用哈尔小波函数对剩余电流信号进行小波包变换后，选取发生触电故障前2个工频周期的剩余电流信号，依据式（3）和式（4），计算供电回路的正常剩余电流中各频段能量，如图2a所示。该小波包分解后能量集中在第0～3个频带表示的156.25 Hz以下低频信号分量内，高频信号分量能量对应较小，且逐渐随着频率的升高而减小。

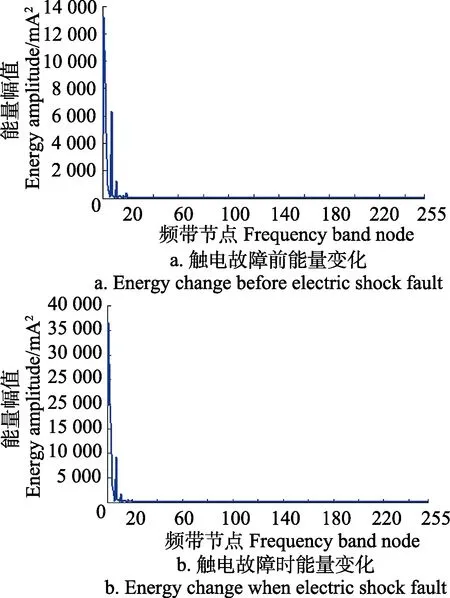
图2 剩余电流各频带能量Fig.2 Band energy of each frequency of residual current

同原理，选取发生生物触电故障时前后各1个工频周期，共2个工频周期的剩余电流信号，计算其小波包变换后各个频段能量，如图2b所示。发生触电故障时经小波包变换的剩余电流各频带能量依然集中在低频带内，但相对于未发生触电故障信号结果更为分散。统计312.475 Hz以下低频分量，即第0～7个频带的能量平均值分别为：20 729.69、52 406.63、14 882.15、33 787.17、2 854.317、4 031.809、4 479.165、9 396.813；其中1频带的基波和3频带的3次谐波，二者能量与触电故障前相比增幅明显，直流分量、2次及4次谐波的频带有相对较大的能量波动。

由图2剩余电流各频带节点的能量变化实例可知，在剩余电流信号中，低频段的能量较高，更为集中在39.062 5～78.125 Hz和119.2～56.25 Hz频带内，其能量谱能够反映触电故障发生时剩余电流的数特征。在不同频段中不同触电时刻的能量产生了差异，是由于试验时触电电压未稳定在某一确定范围内，同一频段内，特别是低频频段内能量发生突变与算法无关。

因此应用式（5）对各频带的节点能量进行归一化处理。触电前（未发生触电故障2个工频周期）与触电时（发生触电故障时刻前后各1个工频周期）剩余电流信号进行小波包8层分解变换，计算不同频带的能量谱（归一化），统计各频带能量占有比例，如图3所示。

从图3中剩余电流信号在触电前和触电时各阶段，分别进行8层的小波包分解，并得到各不同频段的能

量归一化占有比例。图3a剩余电流在触电故障前，通过小波包变化其能量的归一化占有比集中在较低频带内，计算312.475 Hz以下各频带分量的能量比例为：11.07、31.38、20.07、11.37、2.31、1.32、0.16、15.11；同理图 3b中发生触电故障时能量归一化比例为：17.14、32.21、17.42、14.22、2.92、2.26、0.15、8.09。各阶段频带节点总能量占有比例依次减少，频率在468.725 Hz以下各频带的能量占有比之和达到96.53%和95.72%，其中第1频带至第3频带中能量相对最集中。图3c中能量归一化比例之差，能够反映生物触电故障发生前后所引起各个频带能量谱波动的变化程度，对于频率在312.475 Hz以下各频带影响较大。统计各频带能量比例之差的绝对值，计算其平均值为：5.58、9.05、5.93、9.00、0.87、1.65、1.19、3.65。能量谱起伏最显著的频带为：0～156.25 Hz和273.412 5～ 312.475 Hz，其中，39.062 5～78.125 Hz和 119.2～156.25 Hz两频带的能量占有比之差的绝对值，其均值波动幅度达到9.05和9.00尤为突出。综合分析剩余电流小波能量谱变化规律可知，应选取作为生物体触电故障的小波包能量谱特征向量。

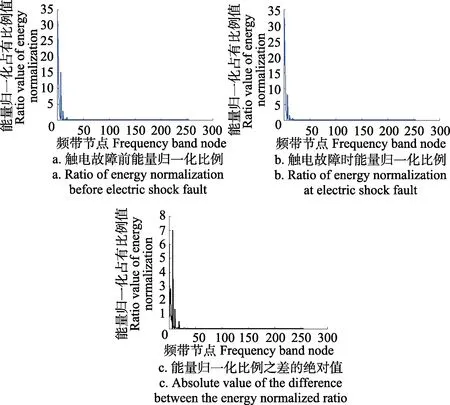
图3 剩余电流小波包频带能量占有比例变化Fig.3 Residual current wavelet packet frequency band energy ratio change

2 基于小波包能量特征触电故障检测

剩余电流经能量谱特征向量，在生物体触电故障发生时的突出变化，可作为生物触电故障检测的依据。定义T-1和T0分别为无触电故障发生的2个顺序时间阶段，且各自时长具有2个工频周期，T1为发生触电故障时前后各1个工频周期的时间阶段，Fi(T-1,T0)表示在发生触电故障前，第i个频带能量占有比例之差的绝对值；Fi(T0,T1)表示在发生触电故障时，第i个频带能量占有比例之差的绝对值。因此触电时与触电前的剩余电流信号，在第i个频带的能量谱变化率Ri为

将剩余电流信号进行8层小波包分解后，计算频率在312.475 Hz以下各频带节点的频谱特征，如表1所示。

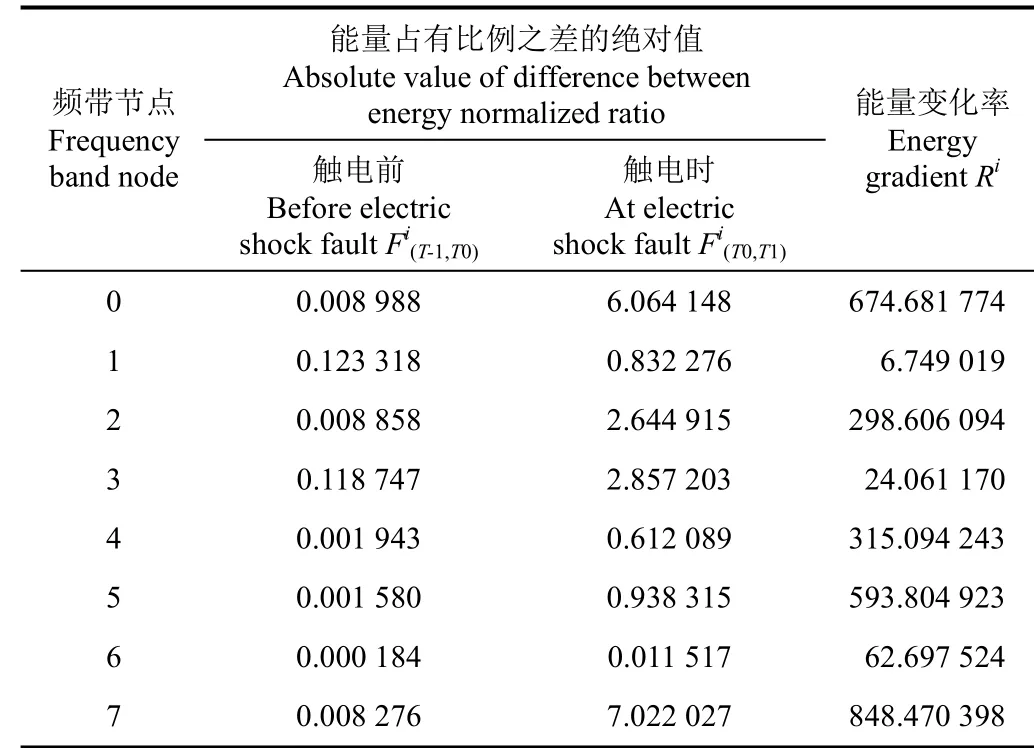
表1 剩余电流8层分解的能量特征变化Table 1 Changes of energy characteristics based on 8-dimentional decomposition of residual current

随机选取四肢哺乳类动物为对象的生物体直接触电故障和常见植物为代表的常见介质触电故障共 200组剩余电流信号，应用哈尔正交小波函数对其进行 8层分解重构，计算频率在312.475 Hz以下各频带的能量突变量 ΔR值范围 4.8786～118.354 7，其平均值为41.184 983。为保证触电故障检测的全面准确，设置能量突变量ΔR的阈值为4，作为触电故障发生的判断依据。同时另外随机选取100组剩余电流信号对本文提出的触电故障检测方法进行验证，仿真试验准确率达到100%，所以基于小波包能量谱特征的触电故障检测是一种准确可靠的新方法。

3 基于量子神经网络的触电故障类型识别

3.1 量子神经网络结构

由于生物体触电故障类型与剩余电流之间映射关系，难以用精确数学模型表达，本文利用量子神经网络中量子神经元具有多个量子能级的激活函数，可自适应地确定样本数据中潜在的模糊决策规律，将其作为一种解决触电故障类型识别模型。研究中采用3层量子神经网络模型，网络结构中隐含层为量子神经元[29]，如图4所示。

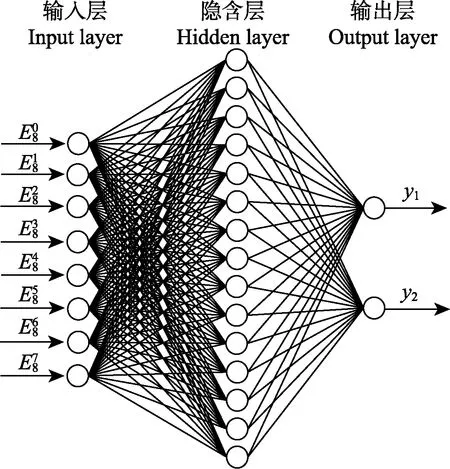
图4 量子神经网络结构Fig.4 Quantum neural network structure

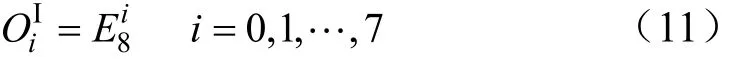
第二层为隐含层。该网络隐含层各节点的激励函数为sigmoid函数f，每个隐含层节点的离散级别数为n，陡度因子为α，输入层到隐含层的连接加权为ωij，各节点阈值为aj，量子间隔为为隐含层第j个节点的输出

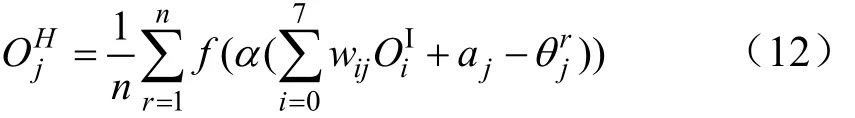
式中

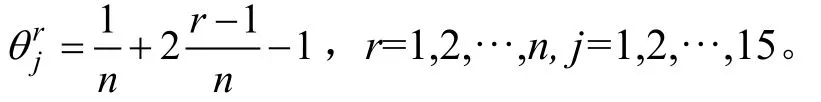
第三层为输出层。该层各节点的线性函数为g，隐含层到输出层的连接加权为vjk，各节点的阈值bk，则为输出层第k节点的输出

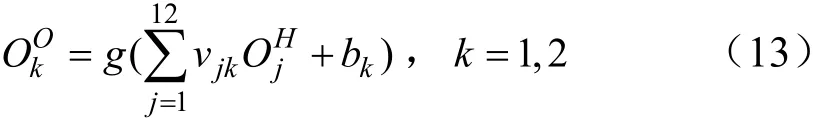
3.2 网络参数更新算法

量子神经网络模型的学习算法，采用梯度下降法学习[30]训练网络参数。调整误差函数定义

式中Y为实际输出，D为期望输出，则量子神经网络可调整参数学习规则为

式中η为学习速度；β为惯性系数；t为学习次数。利用该学习算法可对隐含层各节点的量子间隔进行更新。设C1,C2,···,Cm是实数分为m个类对应的数据集，类Cm隐含层第j个节点的输出值的误差为

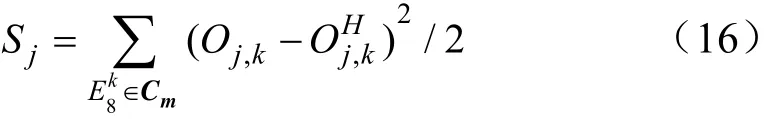
表示输入时隐含层第j个

节点的输出，其中|Cm|为类Cm的基数。

则可得到第j个隐含层节点的第r个量子间隔的更新式的表达式

式中μ为量子间隔更新学习率。

以上给出了量子神经网络中隐含层的量子神经元的量子间隔更新算法。

3.3 触电故障类型识别仿真应用

由于低压电网发生生物体触电故障时，可能构成触电者生命安全，此时剩余电流保护装置必须及时准确动作，而对于常见介质触电故障，可采取其他有效措施，所以开展生物体直接触电和常见介质触电2大类触电故障类型识别方法的研究，对于防止触电伤亡事故，避免发生因漏电而引起的电气火灾，保证电网安全可靠供电具有非常重要的作用。

3.3.1 获取能量谱特征样本

应用哈尔正交小波包函数，对剩余电流中进行 8层尺度分解，计算0～312.475 Hz各频带的8维度频谱特征向量将其作为生物触电故障类型的识别依据。在触电故障类型研究过程中，选取生物体直接触电和常见介质触电 2类触电故障各200组数据，共计400个样本。计算在发生触电故障前后各1个工频周期内，剩余电流信号能量谱特征的8维度向量，如表2所示。

3.3.2 确定网络结构参数

依据3.1节中量子神经网络结构，确定基于小波包变换的8维度能量特征，决定了网络输入层节点数为8；触电故障类型2位二进制编码，即输出层节点数为2；根据Kolmogorov定理和实际试验确定了隐含层量子神经元节点为15；所以生物体触电故障类型识别的神经网络结构为8-15-2型。在网络实际训练时，设定目标精度为0.001，学习速度为0.8，惯性系数为0.6，最大学习次数为 40 000，其中量子间隔更新学习率为0.6，陡度因子为 1，各层的激活函数采用 Sigmoid函数，隐含层节点的量子神经元具有3个离散级。

表2 基于小波包变换的能量谱特征（归一化）Table 2 Energy spectrum characteristics based on wavelet packet transform (normalized)

3.3.3 网络参数训练

选取生物体直接触电和常见介质触电2种触电故障各150个样本，共计300个样本为训练集。利用传统 BP神经网络和文中提出的量子神经网络分别进行触电故障类型识别模型的参数训练。在目标精度和网络结构参数均相同的前提下，量子神经网络迭代次数为1 437次，满足精度误差为0.000 998 92，而传统BP神经网络迭代次数为 23 562次，满足精度误差为0.001，量子神经网络在平均迭代次数和精度误差均优于BP网络。

本文以多能量级的量子神经元构建的神经网络，利用多个量子能级的激励函数叠加来表示多种状态，避免了传统前馈 BP神经网络在训练过程中易出现局部极小值的弊端，因此加快了训练速度。

3.3.4 触电故障类型识别仿真与评价

仿真试验过程中，量子神经网络的实际输出值，所对应触电故障类型二进制编码的解码映射规则为：当网络输出y1≥y2时，对应触电故障类型编码为10，表示生物体直接触电故障；当网络输出y1＜y2时，对应触电故障类型编码为01，表示常见介质触电故障。

通过生物体直接触电和常见介质触电2种触电故障各自剩余的50个样本，共计100个样本为测试集，对训练好的触电故障类型自动识别的神经网络进行验证。该量子神经网络所计算的网络输出值和期望输出值的误差相对较小，绝对误差范围为–0.272 5～0.193 2，其平均值为0.027 4。对于生物体直接触电故障和常见介质触电故障类型的识别准确率达100%，实现了生物体触电故障类型与剩余电流之间，难以用精确数学模型表达的映射关系。

为测试及评价基于小波包变换和量子神经网络模型（wavelet packet transformation-quantum neural network，WPT-QNN），对于触电故障类型检测性能的效果，评价性能指标取触电故障类型识别模型的检测值偏离实际值偏差平均数的平方根，即均方根误差（root mean square error，RMSE）。在相同条件下，与经验模态分解和模糊神经网络模型（empirical mode decompositionfuzzy neural network，EMD-FNN）进行性能比较，同样设定目标精度为 0.001。本文提出的 WPT-QNN与EMD-FNN识别方法，进行触电故障类型识别，仿真试验准确率均为100%，比较2种触电故障类型识别方法的性能参数结果，如表3所示。

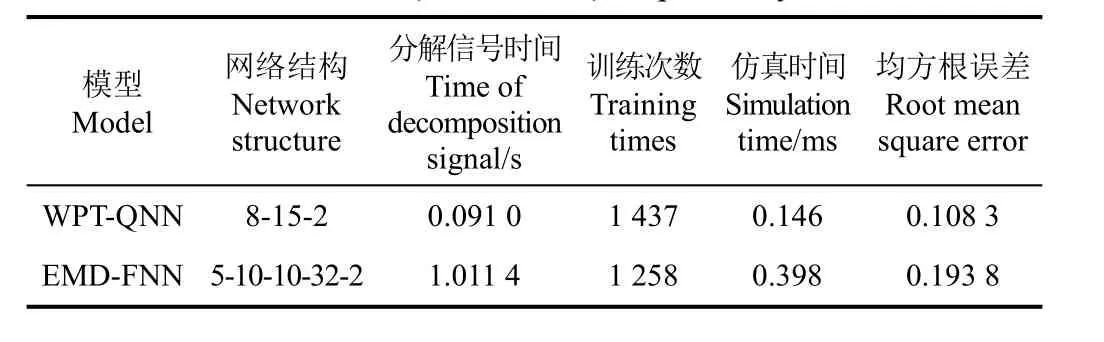
表3 WPT-QNN与EMD-FNN识别触电故障类型仿真结果Table 3 Simulation results of identifying electric shock type using wavelet packet transformation-quantum neural network(WPT-QNN) and empirical mode decomposition-fuzzy neural network (EMD-FNN) respectively

从表3中可以看出，2种触电故障类型识别模型的神经网络训练次数比较相近，均方根误差（RMSE）分别为0.108 3和0.193 8。WPT-QNN模型网络结构简单，参数传递层数较少，因此在触电故障类型识别的运算速度上优于EMD-FNN模型。EMD-FNN模型通过经验模态分解剩余电流时，其分解层数范围为4～7层，平均信号分解时间为 1.011 4 s，本文应用小波包变换对剩余电流进行8层分解时间仅为0.091 0 s，剩余电流分解时间节省了0.920 4 s，仿真时间加快了0.252 ms，避免了EMD-FNN模型在分量数量及耗时上存在的不确定性。所以基于小波包变换和量子神经网络的触电故障类型识别模型，快速高效地实现了触电故障类型的识别，满足了剩余电流保护技术中及时准确识别触电故障类型的要求。

4 结 论

本文首先应用小波包变换提取了剩余电流的小波包能量谱8维度特征向量，以此数字特征为有效信息源，实现了生物体发生触电故障的准确检测，完成了触电故障类型的有效识别。1）生物体触电信号分解为8层共256个频带能量节点，当发生触电故障时能量谱起伏最显著的频带为：0～156.25 Hz和 273.412 5～312.475 Hz，选取了生物触电故障信号的小波包能量谱8维度特征向量，将剩余电流信号有效信息转换为能量数字特征。2）通过触电故障前后各频带能量占有比之差的绝对值，计算其平均值的变化率，进行触电故障检测的准确率达到100%，建立了基于小波包能量谱特征的触电故障检测方法。3）应用量子神经网络实现了剩余电流电流与触电故障类型之间潜在规律的映射关系，该网络隐含层采用多个量子能级的量子神经元，自适应地确定样本数据中潜在的模糊决策规律，其仿真试验准确率为100%，均方根误差（RMSE）为0.108 3。本文提出的 WPT-QNN(wavelet packet transformationquantum neural network，WPT-QNN)与 EMD-FNN(empirical mode decomposition- fuzzy neural network)模型相比较，剩余电流分解时间节省了 0.920 4 s，仿真时间加快了 0.252 ms，能够满足剩余电流保护技术中快速准确动作的实际要求，为快速高效地识别触电故障类型提供了一种新的检测方法。为研发基于生物体触电电流而动作的新型剩余电流保护装置，保证低压电网的人身安全和安全运行提供可靠的理论依据和方法支撑。

[1] 杜松怀，张筱慧. 电力系统接地技术[M]. 北京：中国电力出版社，2011.

[2] 夏越，杜松怀，李春兰. 中国剩余电流保护技术与装置的发展趋势[J]. 农业工程学报，2010，26(增刊2)：151－155.Xia Yue, Du Songhuai, Li Chunlan. Development tendency of residual current protection technology and device in China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(Supp.2):151－155. (in Chinese with English abstract)

[3] Taylor C J, Twynham S C, Powell S C. A magnetoresistive residual current sensor[C]// IEE Colloquium on Advances in Sensors, London, UK. IEE, Stevenage, United Kingdom,1995, 232: 1－6.

[4] Brennan P V. Residual current device with high immunity to nuisance tripping[J]. IEE Proceedings on Circuits Devices and Systems, 1993, 140(2): 140－144．

[5] 关海鸥，杜松怀，苏娟，等．一种触电信号的自动快速检测模型[J]．电网技术，2013，37(8)：2328－2335．Guan Haiou, Du Songhuai, Su Juan, et al. An automatic and quick detection model of electric shock signals[J]. Power System Technology, 2013, 37(8): 2328－2335. (in Chinese with English abstract)

[6] Luis M, Ryszard R, Franjo C. Design of a magneto-optic residual current device using aqueous ferrofluid as the sensing material[C]//Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference. Italy: Institute of Electrical and Electronics Engineers Inc, 2004: 804－807.

[7] Su Juan, Xia Yue, Du Songhuai, et al. Study on identifying method of electric shock current amplitude based on Independent Component Analysis[C]//2011 International Conference on Advanced Power System Automation and Protection, Beijing, 2011, 1034－1038.

[8] 李春兰，杜松怀，苏娟. 一种新的基于小波变换和混沌理论的触电信号检测方法[J]. 电力系统保护与控制，2011，39(10)：48－55.Li Chunlan, Du Songhuai, Su Juan. A novel detecting method of electric shock signal based on wavelet transform and chaotic theory[J]. Power System Protection and Control,2011, 39(10): 48－55. (in Chinese with English abstract)

[9] 关海鸥，李伟凯，杜松怀，等. 基于 Hilbert-Huang 变换的生物触电电流检测模型[J]. 农业工程学报，2017，33(14)：202－209.Guan Haiou, Li Weikai, Du Songhuai, et al. Detection model of biological electric shock current based on Hilbert-Huang transform[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017,33(14): 202－209. (in Chinese with English abstract)

[10] 李春兰，苏娟，杜松怀，等. 基于小波分析和 BP神经网络的触电信号检测模型[J]. 农业工程学报，2010，26(增刊2)：130－134.Li Chunlan, Su Juan, Du Songhuai, et al. Detecting model of electric shock signal based on wavelet analysis and BP neural network [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010,26(Supp.2): 130－134. (in Chinese with English abstract)

[11] 韩晓慧，杜松怀，苏 娟，等. 基于参数优化的最小二乘支持向量机触电电流检测方法[J]. 农业工程学报，2014，30(23)：238－245.Han Xiaohui, Du Songhuai, Su Juan, et al. Determination method of electric shock current based on parameteroptimized least squares support vector machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(23): 238－245. (in Chinese with English abstract)

[12] 王金丽，刘永梅，杜松怀，等．基于剩余电流固有模态能量特征的生物触电故障诊断模型[J]．农业工程学报，2016，32(21)：202－208．Wang Jinli, Liu Yongmei, Du Songhuai, et al. Fault diagnosis model for biological electric shock based on residual current intrinsic mode function energy features[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(21): 202－208. (in Chinese with English abstract)

[13] Eissa M M. A novel digital directional transformer protection technique based on wavelet packet[J]. IEEE Transactions on Power Delivery, 2005, 20(3): 1830－1836.

[14] 刘子洋，王桂英，吴鹏飞. 基于小波包变换的暂态电能质量扰动信号分析[J]. 沈阳农业大学学报，2013，44(1)：118－121.Liu Ziyang, Wang Guiying, Wu Pengfei. Power quality disturbance signal analysis based on wavelet packet transform in transient[J]. Journal of Shenyang Agricultural University,2013, 44(1): 118－121. (in Chinese with English abstract)

[15] Vatansever Fahri, Ozdemir Ayhan. Power parameters calculations based on wavelet packet transform[J]. International Journal of Electrical Power and Energy Systems, 2009,31(10): 596－603.

[16] 卢继平，徐兵. 基于小波包能量相对熵的配电网单相接地故障区段定位[J]. 电力系统保护与控制，2012，40(20)：26－32.Lu Jiping, Xu Bing. Single-phase earth fault section location based on wavelet packet energy relative entropy in distribution network[J]. Power System Protection and Control, 2012, 40(20): 26－32. (in Chinese with English abstract)

[17] Rioul O, Vetterli M. Wavelets and signal processing[J]. IEEE Signal Processing Magazine, 1991, 8(4): 14－38.

[18] Chan H P E. Application of neural-network computing in intelligent alarm processing[J]. In: 1989 Power Industry Computer Application Conference. Seattle: IEEE, 1989, 246－251.

[19] 吴欣，郭创新. 基于贝叶斯网络的电力系统故障诊断方法[J]. 电力系统及其自动化学报，2005，17(4)：11－16.Wu Xin, Guo Chuangxin. Power system fault diagnosis approach based on bayesian network[J]. Proceedings of the CSU-EPSA, 2005, 17(4): 11－16. (in Chinese with English abstract)

[20] 林圣，何正友，臧天磊，等. 基于粗神经网络的输电线路故障分类方法[J]. 中国电机工程学报，2010，30(28)：72－80.Lin Sheng, He Zhengyou, Zang Tianlei, et al. Novel approach of fault type classification in transmission lines based on rough membership neural networks[J]. Proceedings of the CSEE, 2010, 30(28): 72－80. (in Chinese with English abstract)

[21] 李孝全，庄德慧，张强. 基于粗糙径向基神经网络的电网故障诊断新模型[J]. 电力系统保护与控制，2009，37(18)：20－24.Li Xiaoquan, Zhuang Dehui, Zhang Qiang. A new fault diagnosis model of electric power grid based on rough radical basis function neural networks[J]. Power System Protection and Control, 2009, 37(18): 20－24. (in Chinese with English abstract)

[22] 张举，王兴国，李志雷. 小波包能量熵神经网络在电力系统故障诊断中的应用[J]. 电网技术，2006，30(5)：72－76.Zhang Ju, Wang Xinggou, Li Zhilei. Application of network based on wavelet packet-energy entropy in Power system fault diagnosis[J]. Power System Technology, 2006, 30(5):72－76. (in Chinese with English abstract)

[23] 李东敏，刘志刚，苏玉香，等. 基于多小波包和人工神经网络的电力系统故障类型识别[J]. 电力自动化设备，2009，29(1)：99－104.Li Dongmin, Liu Zhigang, Su Yuxiang, et al. Fault recognition based on multi－wavelet packet and artificial neural network[J]. Electric Power Automation Equipment,2009, 29(1): 99－104. (in Chinese with English abstract)

[24] 滕召胜，罗志坤，孙传奇，等. 基于小波包分解与重构算法的谐波电能计量[J]. 电工技术学报，2010，25(8)：200－206.Teng Zhaosheng, Luo Zhikun, Sun Chuanqi, et al. Harmonic energy measurement based on wavelet packet decomposition and reconstruction algorithm[J]. Transactions of China Electrotechnical Society, 2010, 25(8): 200－206. (in Chinese with English abstract)

[25] 史秋亮，林江. 基于小波包分解与能量特征提取的相关分析法[J]. 声学与电子工程，2010，25(4)：18－20,24.

[26] 刘书俊，李著信，苏毅. 基于小波包能量谱的管道缺陷磁记忆检测信号特征研究[J]. 后勤工程学院学报，2012，28(4)，75－80.Liu Shujun, Li Zhuxin, Su Yi. Study on magnetic memory testing signal feature of pipeline defect based on wavelet packet energy spectrum[J]. Journal of Logistical Engineering University, 2012, 28(4):75－80. (in Chinese with English abstract)

[27] 韩博，马芹永. 煤矿岩巷爆破振动信号能量分布特征的小波包分析[J]. 中国矿业，2013，22(6)：110－114.Han Bo, Ma Qinyong. Wavelet packet analysis of energy distribution feature of blasting vibration signals in coal mine rock roadway[J]. China Mining Magazine, 2013, 22(6)：110－114. (in Chinese with English abstract)

[28] 彭园园. 小波分析在一维信号去噪中的应用[D]. 北京：北京邮电大学，2011.Peng Yuanyuan. The Application of Wavelet Analysis in one-dimensional Signal De-noising[D]. Beijing: Beijing University of Posts and Telecommunications, 2011. (in Chinese with English abstract)

[29] 马晓丹，谭峰，许少华. 基于量子神经网络的马铃薯早疫病诊断模型[J]. 农业机械学报，2011，42(6)：174－178，183.Ma Xiaodan, Tan Feng, Xu Shaohua. Diagnosis method of potato early blight based on quantum neural network [J].Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(6): 174－178, 183. (in Chinese with English abstract)

[30] 关海鸥，衣淑娟，焦峰，等. 农作物缺素症状诊断的正则化模糊神经网络模型[J]. 农业机械学报，2012，43(5)：163－170.Guan Haiou, Yi Shujuan, Jiao Feng, et al. Diagnosis model of crop nutrient deficiency symptoms based on regularized adaptive fuzzy neural network[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(5): 163－170. (in Chinese with English abstract)