发动机喷流对飞行器底部流动影响数值模拟

李国良，杨云军，龚安龙，刘 周

(中国航天空气动力技术研究院，北京100074)

0 引 言

导弹飞行过程中发动机喷流与来流绕流的作用会改变弹体的气动特性，尤其是对底阻特性的影响较大。底阻受到弹体长度、边界层状态、尾部形状、发动机喷流参数、飞行高度和马赫数等因素的影响,在高空高马赫数状态下底部有时会出现正推力。探索飞行器底部复杂流动结构及规律，是近年来研究的热点也是难点之一。在不考虑发动机喷流状态下，超声速底部流动包含膨胀波、自由剪切层、分离涡、激波等多种流动结构，分离区中的大涡结构与激波的相互干扰导致流动呈现高频非定常性。在考虑底部发动机喷流状态下，底部高温高速喷流与来流相互干扰，二次回流区在喷口附近形成了环带，因此与无喷流状态相比，底部发动机喷流改变了底部流场结构及飞行器的气动特性。

底部流动研究涉及两大类问题：无喷流时的底部大分离流动和发动机喷流干扰下的掺混流动。目前国内外研究学者对无喷流状态底部流动开展了大量研究。肖志祥等[1]采用RANS/LES混合方法研究超声速底部流动，对包含丰富流动结构和复杂流动机理的导弹类超声速底部流场进行数值分析。高瑞泽等[2]采用LES/RANS混合方法及Smagorinsky-BL及Vreman-BL模型对超声速底部流动开展了计算，获得了较好的速度型及底面压力分布结果。朱德华等[3]采用二阶总变差不增格式(TVD)及二阶Runge-Kutta法模拟了高超声速钝锥底部尾迹流场，观察到了底部出现了非定常周期性流动，呈现流动的不稳定性。国外的研究学者Soshi等[4]、Pramod等[5]、Franck等[6]、Krishnendu[7]、Soo等[8]对底部大分离流动开展了计算方法的适用性研究，并与试验进行了比较。

[4-8]的计算结果表明，RANS方法不能完全准确模拟底部流动大分离特性。但本文的计算模型底部均带有喷管，喷管的存在实际削弱了底部流动的大分离特性，呈现了定常的特性。根据参考文献[9-11]，RANS方法适用于此类问题的数值模拟。Bannink等[9]、Bakker等[10]采用了冷喷方法开展钝锥旋成体底部流场计算，计算方法为RANS结合不同的湍流模型，包括S-A、k-ω、剪切压力传输湍流模型(SST)等，通过与试验结果的比较得出采用SST湍流模型获得的结果与试验一致性最好。林敬周等[11]采用二阶无波动无自由参数的耗散差分(NND)格式，B-L代数模型对文献[9-10]中的外形开展了底部喷流对来流干扰的研究，结果表明有无喷流对底部流场结构影响很大，同时喷流对底部压力分布有显著影响。田耀四等[12]采用单组分变比热比二维轴对称方程对发动机喷流开展了数值研究，对不同飞行高度及飞行速度的尾喷流激波流场特性进行了详细分析。

依据文献调研发现，国内外在考虑底部发动机喷流干扰下的掺混流动数值模拟研究较少，而且多是采用冷喷方法，即认为来流与喷流为同一介质，通常为空气。本文建立两组分热喷方法，即来流为空气，发动机燃气为另一种介质。这种计算方案能够更真实地反映燃气的膨胀效应，获得可信度更高的底部压力分布，更好地应用到工程问题中。

本文采用RANS结合SST湍流模型，并与试验数据进行比较，验证方法的准确性。同时针对本文选用的飞行器外形比较冷喷与热喷两种处理方法对计算结果的差异。最后采用热喷方法对其超声速底部流动开展计算研究，并与监测点试验数据进行比较。选定来流马赫数2.5，开展不同飞行高度及发动机总压对燃气扩散及底部流场的影响研究。

1 计算方法与算例验证

1.1 方法介绍

湍流采用SST两方程模型，Roe的Riemann近似解算器计算无黏通量。时间推进采用上下对称的高斯-赛德尔(LU-SGS)方法。热喷计算时采用双组分的三维Navier-Stokes方程，如下所示：

(1)

(2)

(3)

其中，

(4)

式中：V为逆变速度，u，v，w为三个速度分量，ni为单位矢量在坐标系下的分量;p为压力，E为总能，ρ为密度，H为总焓;yi为第i种气体的质量分数,Hi为第i种气体的总焓，Di为第i种气体的扩散系数;ρD=μl/Scl+μt/Sct,μl为层流黏性系数，μt为湍流黏性系数，Scl为层流施密特数，Sct为湍流施密特数;τij为应力张量项，qi为热传导项。

在考虑冷喷计算时，喷流与来流为同一种介质，即空气，热喷控制方程褪化为常规Navier-Stokes方程。

1.2 喷流算例验证

选取经典试验开展方法验证，试验模型为轴对称钝锥外形[9-10]，底部喷管出口与喉部面积比为10.7584，进口与喉部面积比为9,如图1所示。

来流马赫数Ma∞=1.96，静压p∞=28300 Pa，攻角α=0。图2所示为无喷流时底部流线，在底部存在两对分离涡。图3所示为无喷流时模型柱体部分压力系数计算与试验[9]的比较。纵坐标压力系数为测点压力与来流压力的比值(下同)。从图3可以看出，计算值与试验值一致性较好，总体误差控制在0.5%以内。

在考虑喷流条件下，计算了压力比(喷管进口总压pin,t与来流静压p∞之比)为12.9和44.0两种情况，喷流介质为高压空气。图4为无喷流及两种压力比三种情况下的计算值与试验值的比较。横坐标表示为底部位置径向坐标与模型半径的比值。在无喷流时，底部计算压力系数与试验值的总体误差控制在8%以内，压力比12.9时误差控制在2.5%以内，压力比44.0时误差控制在5.5%以内。从数值比较来看，本文所建立的来流干扰条件下发动机底部喷流数值方法是准确的。同时计算与试验都表现出随着压力比的不断增加，底部的压力系数逐渐下降的趋势。这表明随着压力比增加，喷流气体对底部流场的引射作用增强。还可以看出，三种情况下，底部压力系数不随径向位置的改变发生变化，基本保持恒定。图5为压力比44.0时底部流场流线，从图5可以看出，高速喷流气体削弱了底部分离区域的大小，同时改变了底部流场的涡结构。

图6为流场当地p与p∞比值的等值线云图，此时的压力比增加到349，底部流动出现了明显的流动特征，即出现了桶状激波(图中标注为1)与羽流激波(图中标注为2)。这与参考文献[9-10]的试验结果与计算结果一致。

2 飞行器外形与冷/热喷计算方法对比

2.1 飞行器外形参数

计算模型为图7所示的三维轴对称尖锥外形飞行器，底部为发动机喷管。模型总长为10 m，柱体直径为1.45 m,计算网格采用分区多块结构方式。监测传感器位置位于模型底部xy对称面上，距离喷管中心线0.65 m。

2.2 冷喷与热喷计算结果对比

对于发动机喷流问题处理方式分为等效冷喷与热喷。热喷方法中来流与发动机燃气均为量热完全气体。冷喷等效通常有两种方法：1)出口动量、压力比相等，马赫数不同；2)出口动量、马赫数相等，压力不同。

以计算来流条件：来流温度T∞=227 K，Ma∞=1.8，P∞=29400 Pa，α=0，Pin,t=6.0×106Pa，燃烧室总温Tin,t=3500 K，燃气气体常数Rc=284 J/(kg·K)为例来说明两种冷喷等效方法的差异。

等熵流Ma和面积A之间的关系式：

(5)

喉道Mat=1，发动机燃气γ=1.1，出口面积Aout与喉部面积At比11.6，半径比3.40。得到出口Maout=3.09。

出口静压Pout与Pin,t的关系式：

(6)

式中:Pout=81970 Pa。

出口静温Tout与Tin,t的关系式：

(7)

式中:Tout=2369 K。

1)动量相等，压力比相等，马赫数变化

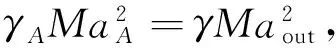
2)动量相等，马赫数相等，压力变化

出口马赫数相等，等效出口MaA=Maout=3.09。出口动量相等，γAPA=γPout，空气γA=1.4，得到出口PA=64405 Pa，与实际Pout相差21.4%。得到空气下的出口与喉部面积比4.61，半径比2.15。在此条件下根据式(3)得Pin,t=2706116 Pa，总温不变。

综上所述，动量、压力比相等时，出口马赫数与实际值差11.3%；动量、马赫数相等时，出口压力与实际值差21.4%。因此选取第1种相似条件，即动量、压力比相等更为合适。在此相似条件下喷管进口Main=0.49，静压Pin=1722166 Pa， 静温Tin=3340 K。

图8为喷管原始形线、压力比相等形线、马赫数相等形线示意图。图9为采用冷喷与热喷方法计算的喷管出口的马赫数分布曲线，与理论计算的结果一致性较好，热喷方法计算的喷管出口马赫数平均值为3.10，与理论值的误差为0.3%。冷喷方法计算的喷管出口马赫数平均值为2.80，与理论值的误差为2.2%。

采用冷喷方法与热喷方法开展计算结果的对比分析。图10为冷喷方法与热喷方法的底部流线图，从图中可以看出，两种方法流场结构基本相同，在底部凹腔内形成一对主分离涡及小分离涡。图11为两种方法计算值与试验值的定量比较。与第1.2节算例验证类似，底部压力系数随着y坐标的变化基本保持恒定，表明底部的压力相对均匀。监测点的试验压力系数-0.147，冷喷方法监测点压力系数-0.236，与试验误差为60.5%。热喷方法监测点的压力系数-0.162，与试验误差10.2%。造成误差差异的原因为通过热喷方法计算保持了原来喷管的外形，喷管出口位置的倾斜角度为14.75°。冷喷方法改变了喷管外形，喷管出口位置的倾斜角度减小为9.27°。阻碍了喷管出口的高压气体向空腔内扩散，因此冷喷方法计算的压力系数值较热喷方法要低。

采用热喷方法计算得到的压力数据与试验值一致性较好，表明本文采用的两组分热喷RANS方法是可靠的。燃气的组分分布无法直接测量，但是燃气向底部扩散，直接影响底部压力的分布。从压力比较的结果可知本文采用的方法适用于燃气组分分布的数值模拟。

图12为同一算例采用热喷方法计算得到的发动机燃气尾流质量分数空间分布，燃气尾流呈羽状分布逐渐向周围扩散。

3 飞行器底部流场分析

采用热喷方法对飞行器开展Ma∞=2.5典型状态不同飞行高度H及Pin,t对喷流及底部流场的影响研究。

3.1 进口总压Pin,t变化

H=15 km不变，改变Pin,t，5种条件分别为6.0 MPa，7.2 MPa，8.4 MPa，9.6 MPa，10.8MPa，研究发动机燃气参数对底部扩散及压力分布的影响。

图13为底部压力系数随Pin,t变化曲线，随着Pin,t提高，底部压力系数逐渐增加，同时5种条件下底部压力分布均各自保持基本恒定。

图14为底部燃气质量分数随Pin,t变化曲线，随着Pin,t提高，壁面处的燃气质量分数变化较小，在0.155～0.165之间。在底部凹腔x=9.9 m壁面处燃气质量分数同样基本保持不变，在0.163左右。其余位置燃气质量分数逐渐提高。从图14可以看出，发动机燃气向底部凹腔内扩散，壁面处的燃气浓度最高，而且达到一个额定值后，随Pin,t提高基本不变。

3.2 飞行高度H变化

Pin,t=7.2 MPa不变，改变H，6种条件分别为11 km，13 km，15 km，17 km，19 km，21 km。从图15可以看出，Pin,t不变，底部压力系数随着H的增加单调增加。在H=21 km时底部压力系数为0.0147，即底部出现正推力。正推力的出现有可能改变飞行器的飞行弹道，在设计阶段需要提前开展评估。

图16为Ma∞=2.5，H=11 km，13 km，15 km，17 km，19 km，21 km时喷管出口下游中心线马赫数分布。图中坐标轴x代表中心线上一点与喷管出口中心点的距离，x=0代表喷管出口中心点处。从图16可以看出,来流马赫数一定，喷管出口中心线上发动机燃气最大马赫数随着飞行高度增加不断后移且数值不断增大。

图17、图18为Ma∞=2.5，H=11 km，21 km时底部马赫数云图，从图中可以看出,H=11 km时发动机燃气最大马赫数为4.7，H=21 km时发动机燃气最大马赫数为5.9，同时发动机燃气在H=21 km时膨胀效应更强，高马赫数的范围更广。

图19为H=11 km在距喷管出口0.2 m,0.5 m,1.0 m,2.0 m处沿y方向的燃气质量分数曲线。图20为H=21 km在距喷管出口0.2 m,0.5 m,1.0 m,2.0 m处沿y方向的燃气质量分数曲线。H=11 km，在x=1.0 m处燃气的膨胀范围±1.2 m，在x=2.0 m处燃气的膨胀范围±1.35 m。H=21 km，在x=1.0 m处燃气的膨胀范围±1.7 m，在x=2.0 m处燃气的膨胀范围±2.1 m。由于本文选用的飞行器长度较长，底部的环境压力恢复为来流压力，飞行高度增加，来流压力减小，底部环境压力对发动机燃气的约束减弱，发动机燃气的膨胀效应增强，高速区整体向后移动。

4 结 论

本文建立了考虑发动机喷流的三维冷喷与两组分热喷数值模拟方法，在相同的来流与发动机参数条件下，进行了冷喷与热喷方法的对比分析，两组分热喷方法获得的数据与试验值一致性较好，较冷喷方法精度有明显提升。采用热喷方法，对飞行器开展了飞行高度及喷管进口总压对喷流及底部流场的影响研究。随着喷管进口总压增加，底部压力系数逐步提高。最高燃气质量浓度位于底部壁面处，而且达到一个额定值后，不随总压提高而变化。随着飞行高度的增加，底部压力系数单调增加，喷管出口中心线上发动机燃气最大马赫数不断后移且数值不断增加，在一定的飞行高度，底部压力系数由负转正，即底部会出现正推力。本文计算方案把燃气作为一种均质流体，因此不能完全表征燃气的实际流动特性。未来需要开展发动机燃气多组分数值方法的研究工作。

参考文献

[1] 肖志祥, 符松. 用RANS/LES混合方法研究超声速底部流动[J]. 计算物理, 2009, 26(2):221-230. [Xiao Zhi-xiang, Fu Song. Study on supersonic base flow using RANS/LES method [J]. Chinese Journal of Computational Physics, 2009, 26(2): 221-230.]

[2] 高瑞泽, 闫超. LES/RANS混合方法对超声速底部流动的应用[J]. 北京航空航天大学学报, 2011, 37(9):1095-1099. [Gao Rui-ze, Yan Chao. LES/RANS hybird method for supersonic axisymmetric base flow[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(9):1095-1099. ]

[3] 朱德华, 沈清. 钝头体高超声速绕流底部失稳特征数值模拟[J]. 力学学报, 2012, 44(3):465-472. [Zhu De-hua, Shen Qing. Numerical study of the stability of hypersonic base flow over a blunt body and Apollo command module[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(3): 465-472. ]

[4] Soshi K, Kozo F. Computational analysis of the characteristics of subsonic, transonic and supersonic base flows[C]. The 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Canada，June 6-9, 2005.

[5] Pramod S, Graham V C. Numerical investigation of supersonic base flows using DES[C]. The 43rd Aerospace Science Meeting and Exhibit Conference, Reno, USA, January 10-13, 2005.

[6] Francs S, Sebastein D, Philippe G, et al. RANS-LES simulations of supersonic base flow[C]. The 44th Aerospace Science Meeting and Exhibit Conference, Reno, USA, January 9-12, 2006.

[7] Krishnendu S. Eeffect of Reynolds number on detached eddy simulation of hypersonic base flow[C]. The 45th AIAA Aerospace Science Meeting and Exhibit Conference, Reno, USA, January 8-11, 2007.

[8] Soo H P, Sumanta A. An improved formulation ofk-εturbulence models for supersonic base flow[C]. The 17th AIAA Computational Fluid Dynamics Conference, Toronto, Canada, June 6-9, 2005.

[9] Bannink W J, Bakker E M. Base flow/underexpanded exhaust plume interaction in a supersonic external flow[C]. The 8th AIAA International Space Planes and Hypersonic Systems and Technology Conference, Norfolk, USA, April 27-30, 1998.

[10] Bakker P G, Bannink W J. CFD validation for base flows with and without plume interaction[C]. The 40th Aerospace Science Meeting and Exhibit Conference , Reno, USA, January 14-17, 2002.

[11] 林敬周, 李桦. 超声速底部喷流干扰流场数值模拟[J]. 空气动力学报, 2005, 23(4):516-520. [Lin Jing-zhou, Li Hua. Numerical investigation of base jet interaction in a supersonic external flow [J]. ACTA Aerodynamics Sinica, 2005, 23(4): 516-520.]

[12] 田耀四, 蔡国飙, 朱定强, 等. 固体火箭发动机喷流流场数值仿真[J]. 宇航学报, 2006, 27(5):876-880. [Tian Yao-si, Cai Guo-biao，Zhu Ding-qiang，et al. Exhaust plume simulation of solid rocket[J]. Journal of Astronautics, 2006, 27(5):876-880.]