经历建模过程 积累建模经验——以“乘法分配律”的教学为例

江苏南京市雨花台区共青团路小学（210000） 刘正娟

【错误列举】

关于苏教版教材四年级下册的“乘法分配律”，学生在学习的过程中常常出现以下两种错误。

算理理解不到位。如图1，归根结底，不理解算理，也就是不理解乘法的意义。

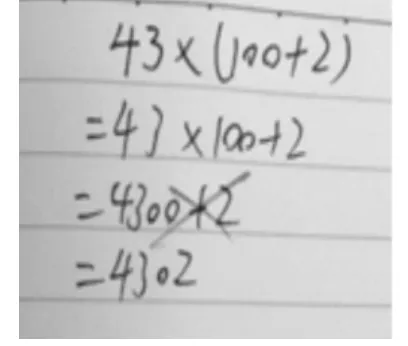
图1

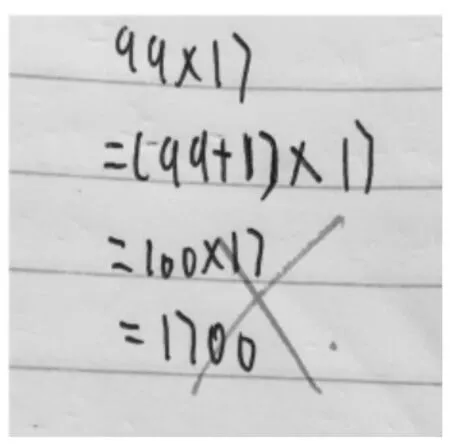
图2

凑整思想的僵化。如图2，学生只是注意到99接近100，没有考虑到这个算式的特点，没有准确分析“这个数”在算式中与其他数之间的运算关系，机械凑整，势必会导致计算结果错误。

学生出现上述这些错误的根本原因在于不理解算式的意义，只是机械模仿，不能按照算理正确地思考简算过程。在多次思考之后，我找到了一种行之有效的方法，那就是从建模的角度出发，聚焦最朴素的算理——乘法的意义，分析学生的错误原因，抓住问题的本质，根治错误。

【教学重构】

片段一：数形结合，建立两式相等关系

1.出示图3，引导学生思考：怎么求这两个图形的面积之和呢？你能想出几种方法？在学生得出两种基本方法后，我写出等式：（6+3）×4=6×4+3×4。

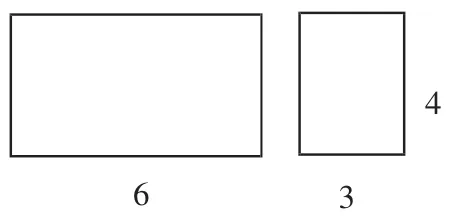
图3

2.让学生从图4中的三个长方形中选出两个，拼成一个大长方形。

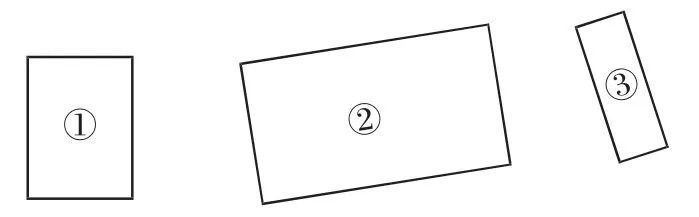
图4

学生通过独立思考、小组活动后得出如图5所示的两个大长方形，并列出算式求出拼好之后的大长方形的面积。

图5

3.引导学生思考：为什么②号长方形和③号长方形不能拼成一个大长方形呢？

4.出示题目“四年级有6个班，五年级有4个班，每个班领24根跳绳。一共领多少根跳绳？”在得出等式（6+4）×24=6×24+4×24后，引导学生归纳总结：这种实际问题也可以用图6来表示，左边的长方形表示四年级一共领了多少根跳绳，右边的长方形表示五年级一共领了多少根跳绳，也可以合在一起看：四、五年级一共有10个班，就是10个24的和。

乘法分配律对学生来说是比较抽象的，将长方形的面积计算与乘法分配律的知识融合在一起，借助几何直观、数形结合，以计算长方形面积为载体建构等式，能使学生在探究的过程中对乘法分配律中的两道算式构成的等式有深入的了解，从而明确探究的方向。学生在交流讨论“为什么②号长方形和③号长方形不能拼成一个大长方形”的过程中，也能体会到“乘法分配律中必须有相同因数”这一重要的数学本质。

片段二：举例验证，明晰两式相等的本质属性

在上述教学的基础上，我组织学生进一步研究：①观察这几组等号两边的算式，你有什么发现？②是不是具有这样特征的算式都能用“=”连接？是偶然还是必然？③请在练习本上写几组具有这样特征的式子；④想一想，像这样的等式写得完吗？

在学生写出大量等式的基础上，我引导学生进行观察和猜想，并且从正反两个方面对得出的猜想进行验证，抽象出结论后，再让学生用数学语言表述其规律。在整个教学过程中，学生经历了乘法分配律的探究过程，抽象、概括的能力得到了发展。学生通过举例验算的方法去感知规律，在真实体验中感受规律，用语言表述规律便水到渠成。

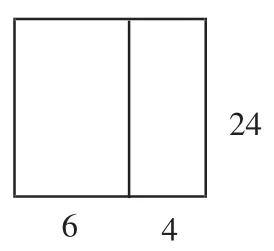
图6

片段三：抽象概括，建立基本模型

师：在前面的研究中，我们已经明晰了两式相等的特征，你能否用自己喜欢的方式表示这个规律呢？

生1：（甲+乙）×丙=甲×丙+乙×丙。

生2：（△+□）×○=△×○+□×○。

生3：（a+b）×c=a×c+b×c。

师：其实，你们的表示方法有异曲同工之妙，都可以用图形（图7）表示出来。

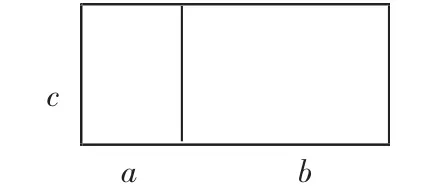
图7

师：既可以用（a+b）×c表示，也可以用 a×c+b×c表示，就得到（a+b）×c=a×c+b×c，这是乘法分配律的直观模型。

师：如果这样的图形由3个、4个或多个长方形组成，那么关系式该怎么改？图形又该怎么画呢？大家试一试吧！

让学生用自己喜欢的方式表示乘法分配律，其目的有三：一是检验学生是否已经正确理解规律；二是让学生再次感受和明晰乘法分配律的结构；三是充分调动学生学习的主动性。乘法分配律是一个数学模型，任何数学模型都是抽象概括的产物，任何一种数学模型也都体现着数学的抽象美和简洁美。但是，数学模型抽象建构完成后，绝不是终点，教师还要引导学生从不同角度对数学模型结构进行精准把握。

【案例反思】

数学模型是沟通数学与生活的桥梁，建立模型的过程就是架设这座桥梁的过程。乘法分配律虽然比较抽象，但在现实生活中有着广泛的应用。本课的教学是通过现实生活情境呈现数学信息，提出数学问题，让学生在探索活动中抽象出乘法分配律的字母表达式，建构乘法分配律的数学模型，并运用这一数学模型解决现实问题。

创设现实情境，感知模型。课程标准指出：建立模型首先要从现实的生活或者具体情境中抽象出数学问题。这说明发现问题和提出问题是数学建模的起点。乘法分配律是一个很抽象的内容，如果没有具体的情境，学生就无法获得体验的机会。本课从现实中的求长方形面积、如何拼长方形、领跳绳的情境入手，引导学生感受两种算法之间的联系，从现实问题中抽象出等式，在初步感知数学模型的同时，也为后续的模型建立积累了丰富的素材。

经历推理过程，初现模型。本课中首先是在得出两组等式后引导学生观察等号两边的算式，并提问：“你发现了什么？是不是所有这种算式都能组成等式？你能想办法验证吗？”演绎推理的过程是从不完全归纳到完全归纳发展的过程，让学生想办法进行验证就是引导学生从意义上来证明猜想的正确性，学生能从问题的实际意义“四、五年级一共领多少根跳绳？”出发，得到“一共有10个班，既是领10个24根”的结论；学生也会利用乘法的意义，从（6+4）个 24就是“6个 24”加“4个 24”的层面来理解。在这样的推理过程中，学生积累了乘法分配律的感性经验，初步建立了乘法分配律的模型。

运用多元表征，建立模型。模型的建立过程包括用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律。因此，引导学生用个性化的表达方式将乘法分配律表示出来，模型才能建立起来。比如，引导学生用自己的方法表示规律，学生就能用文字、图形、字母等方式分别表示三个数，也有学生会用语言表示。这就是学生经历乘法分配律模型建立的过程，在这个过程中，他们体会到了字母表达式的简洁性，也增强了用符号表达规律的意识。