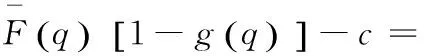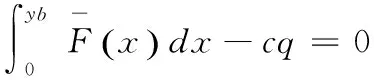考虑风险规避的资金约束供应链最优信用契约设计
2018-03-09骆建文
金 伟,骆建文
(1.浙江财经大学金融学院,江苏 杭州 310018;2.上海交通大学安泰经济与管理学院,上海 200030)
1 引言
当供应链下游零售商面临资金约束时,上游供应商往往向零售商提供交易信用以缓解零售商由于资金约束而造成的经营障碍。作为一种短期融资方式,交易信用在实践中得到广泛应用。在英国,超过80%的B2B贸易以交易信用的方式实现;在美国,一些大型非金融类企业的融资结构中约15%的比例来自于交易信用[1]。在具体行业比如制造业,塔塔汽车公司及丰田汽车公司能够延迟一段时间之后才将全部的采购成本支付给他们的上游供应商[2]。对于供应商而言,交易信用在一定程度上能够激励零售商增加采购量,扩大产品市场份额,进而提高供应商的利润。然而,由于信息不对称和市场需求不确定等原因,供应商在向零售商提供交易信用的过程中可能面临着货款无法完全回收的风险。正因如此,许多供应商在发货前会要求零售商预付部分货款以降低潜在的损失,具体的预付款比例依赖于供应商的自身特点(渠道实力、资金实力及损失风险规避程度)。比如,汽车行业中,汽车制造商要求4S店在下订单时支付所有的货款;而钢铁行业中,供货商会根据批发商的信用等级决策批发商支付部分还是全额货款[3]。
如果零售商需要支付的预付款超过其自有资金水平,除了交易信用融资,零售商还需要选择其他融资比如银行融资。由此可见,供应商提供的交易信用契约不仅影响到自身的收益,还间接影响到资金约束零售商的融资结构。针对这一情况,将交易信用契约与融资结构结合在一起研究非常有必要。为此,本文考虑了风险规避的供应商如何通过提供交易信用契约影响零售商的融资结构,以及零售商如何在给定融资结构下决策最优库存。
与本文相关的文献主要分为两类:一是关于企业运营与融资交互关系研究;二是关于具有风险规避成员的供应链决策研究。在供应链融资领域,已有很多学者涉及企业运营与融资交互关系的研究,相关文献主要包括银行融资下企业的运营与融资决策;交易信用下企业的运营与融资决策。
大多数学者重点从供应链的成员企业以及整个供应链角度,研究银行融资下企业的生产、库存及订货问题。Buzacott和Zhang[4]探讨了当银行是策略型决策者时资金约束企业的运营决策。另外,Xu Xiaodong和Birge[5]将资金约束引入到传统的报童模型中,得到了在非完美的金融市场中,企业的融资决策和生产决策是不能完全分开的结论。这两篇文献在供应链金融领域起到了奠基性的作用,被认为该领域最早的两篇文献。后来,Dada和Hu Qiaohai[6]建立了策略性银行与资金约束零售商的Stackelberg博弈模型,给出了博弈均衡解并提出了系统协调契约。Lai等[7]在供应链上下游企业均有资金约束背景下,建立了具有破产成本的银行融资模型,分析了资金约束对供应链运营模式选择的影响。Kouvelis和Zhao Wenhui[8]研究了破产成本存在时的银行融资问题,探讨了零售商的资金水平与破产风险对最优决策的影响。易雪辉和周宗放[9]分析了银行下侧风险控制下的贷款价值比研究,并刻画了供应链的决策对采购合同抵押价值的影响。王文利等[10]考虑了银行风险控制下,供应链订单融资的最优运作策略。
也有学者从融资角度研究了交易信用在缓解企业资金约束方面的作用。Schwartz[11]最早提出融资动机理论,该理论强调如果卖方比买方更容易接近资本市场,那么卖方有动力向买方提供交易信用。Petersen和Rajan[12]后来从实证角度探讨了供应链上游企业愿意向资金约束的下游企业提供交易信用的主要动机。Burkart和Ellingsen[13]进一步从模型角度解释了交易信用在欠发达信用市场受欢迎的原因。Jamal等[14]通过建立一个确定性模型,给出了交易信用下企业的最优信用期决策。朱文贵等[15]研究了供应商允许零售商延期支付方式下,存货质押融资的最优定价方法。Shi Xiaojun和Zhang Shunming[16]将融资企业的破产风险纳入到经济订货模型中,研究了企业的最优订货与最优信用期决策。陈祥锋[17]指出当零售商存在破产风险且承担有限责任时,交易信用能有效激励零售商增加采购量,从而为资金约束供应链创造价值。Yang和Birge[18]考虑了交易信用在渠道协调和供应链融资方面的角色,发现交易信用作为一种风险共享机制可以提升供应链效率。王文利和骆建文[19]在两阶段随机需求环境下,分析了当供应商向资金约束零售商提供交易信用融资时零售商的最优订货决策。
近年来,一些学者将银行融资与交易信用结合研究,考虑当资金约束企业同时面临这两种融资模式时的融资均衡问题。Kouvelis和Zhao Wenhui[20]考虑了一条由资金约束的制造商和零售商组成的供应链,分别从制造商、零售商以及整个供应链角度比较了银行融资与交易信用。Jing Bin等[21]通过比较交易信用与银行融资得出当制造商的生产成本较低时,零售商的融资均衡为交易信用,否则融资均衡为银行融资。Cai Gang等[22]在供应链下游企业资金约束而上游企业资金充足的假设下研究了交易信用与银行借贷在资金约束供应链中所起的作用以及资金约束的零售商对两种融资方式的偏好。Chen Xiangfeng[23]比较了收益共享契约下的银行融资与延期付款融资,并分析了市场波动性对融资均衡的影响。
以上关于企业运营与融资交互关系的研究往往假设债权人是风险中性的,较少考虑风险规避环境下的供应链融资问题。另外,以上文献或研究某一特定融资模式下的企业运营与融资决策,或研究两种融资模式下的企业融资均衡问题,很少考虑组合融资模式下的企业融资比例分配问题。与上述文献不同的是,本文将决策者的风险偏好引入到融资模型中,分析了风险规避的供应商如何通过设计信用契约影响资金约束零售商的融资结构,文中给出了组合融资模式下的零售商最优银行融资比例以及对应的最优库存决策。
在具有风险规避成员的供应链决策方面,其中决策者普遍具有损失规避性。Schweitze和Cachon[24]对损失规避型效用函数进行了详细的刻画同时给出了相应的性质。Wang和Webster[25]考虑了由一个风险中性的制造商和一个损失规避的零售商组成的供应链,发现零售商的损失规避性导致了传统的供应链协调契约不再适用于损失规避型供应链。Wang和Webster[26]利用损失规避型效用函数刻画单阶段报童模型,并得到了与风险中性报童模型不同的结果,如当缺货成本存在时,损失规避的零售商相比风险中性的零售商会订更多的货。马利军等[27]考虑了损失规避型零售商在供应和需求均不确定环境下,如何通过提前支付策略降低供应不确定性风险。王佳等[28]针对投资者的损失规避特征考虑了风险资产不确定条件下的分布鲁棒投资组合问题。与这些文献类似,本文采用损失规避型效用函数刻画决策者的风险规避性,然而与这些文献不同之处在于,本文从供应链融资角度考虑债权人的损失规避程度对信用契约及融资结构的影响。
本文的研究思路如下:首先构建了一条由一个损失规避型供应商,资金约束零售商以及收支平衡的银行组成的融资系统;其次用逆向归纳法先给出了零售商的最优库存决策及银行的最优利率决策,再通过求解非线性规划问题给出了供应商的最优信用契约参数,进而得到了零售商的融资结构。最后探讨了供应商的损失规避程度与生产成本对最优决策的影响。
2 问题描述与模型假设
考虑由单一供应商和单一零售商组成的一条二级供应链,其中零售商面临的市场需求表现出典型的报童模型特征,即产品的零售价格p在销售阶段保持不变,产品的市场需求量X是不确定的。类似于经典的供应链融资模型[20-23],在需求实现前,零售商以批发价w向供应商采购q数量的产品并以零售价格p销售到需求不确定的市场,其中零售商是资金约束的。不失一般性,参照Jing Bing等[21]和Chen Xiangfeng[23],零售商的资金水平假设为零同时零售价格p假设为1,这种做法简化了数学表达式而不影响相关结论。零售商有两种主要的短期融资方式:对上游供应商延期付款融资以及向银行借贷。一般而言,延期付款融资被称为供应链内部融资,银行借贷被称为供应链外部融资。由于供应商相比于银行更加了解零售商的经营状况,从而延期付款的融资成本往往低于银行融资的成本。基于此,资金约束的零售商首先选择延期付款融资,如果延期付款融资的额度不能满足零售商的融资需求,其再向银行融资差额部分。
本文使用的数学符号如下:
X:市场需求量;
w:供应商设定的批发价(供应商的决策变量);
c:供应商的单位生产成本;
δ:供应商要求零售商的预付货款比例(供应商的决策变量);
q:零售商的订货量(零售商的决策变量);
r:银行设定的贷款利率(银行的决策变量);
λ:供应商的风险规避系数;
yb:银行贷款本息和,也表示零售商能够偿还银行贷款所需的最低市场需求;
ys:零售商能够偿还全部贷款所需的最低需求值;
yL:供应商的利润大于零所需的最低需求值;
p:零售价格,规范化为1;
πs、πR:供应商、零售商的利润;
u(πs):供应商的效用函数。
本文用到的主要假设如下:
H1:供应商对零售商提供信用契约(δ,w),这里δ表示供应商要求零售商的预付货款比例,w表示供应商设定的批发价,比如零售商向供应商采购q单位的产品,零售商需要预付货款δwq,剩余的货款(1-δ)wq待需求实现后再支付给供应商。为了支付预付货款,零售商需要向银行融资δwq。
H2:假设零售商是有限责任的,即在需求实现后,如果零售商的销售收入无法偿还银行贷款或者供应商的剩余货款,零售商只偿还全部的销售收入。这种有限责任的假设在供应链融资领域很常见,比如Kouelis和Zhao Wenhui[20],Jing Bing[21],Cai Gangshu[22],Chen Xiangfeng[23]。
H4: 参照Kouvelis和zhao Wenhui等[20],假设银行处于完全竞争的金融市场中,即银行的期望收入等于期望支出。基于此,下面等式成立:
E[min{1·min{X,q},δwq(1+r)}]=δwq
(1)
式(1)的左边表示银行对零售商放贷所带来的期望收益,其中min{X,q}表示销售数量,1·min{X,q}表示销售金额,δwq表示零售商向银行融资的金额,δwq(1+r)表示零售商需要在销售季结束后向银行偿还的本息和,这里r表示银行贷款利率。式(1)的右边表示银行需要支付给储户的本金和利息(这里为了简化表达式,将银行的无风险利率简化为零)。参数δ反映了供应商承担的库存风险,δ越大,零售商向银行融资的越多,因此供应商承担的库存风险越低。记yb=δwq(1+r),由于我们将批发价p规范化为1,因此后文中我们在比较相关数学变量的时候不考虑其量纲,如q>yb表示订货数量大于数值yb。
根据破产法,当零售商发生破产时,零售商应优先偿还银行贷款,再偿还供应商的剩余货款(即(1-δ)wq)。具体而言,如果市场需求量低于yb,银行只能回收资金额1·X,此时供应商无法回收剩余货款;如果市场需求高于yb但是低于yb+(1-δ)wq,银行可回收贷款,但是供应商只能回收资金额1·X-yb;如果市场需求高于yb+(1-δ)wq,银行可回收贷款同时供应商可回收剩余货款。
H5: 假设供应商具有损失规避的风险偏好,为此引入一个损失规避的效用函数来量化供应商的效用,这种效用函数在经济类及运营管理类文献中被广泛使用[25-26],具体形式如下:
(2)
这里π0是供应商利润的参照水平,不失一般性,假设π0=0。λ≥1刻画了供应商的风险规避程度,λ越大意味着供应商越规避风险。特别地,当λ=1时,供应商是风险中性的。
供应商和零售商进行Stackelberg 博弈,其中供应商是领导者,零售商是跟随者。博弈的顺序为:(1)在t=0时,供应商向零售商提供信用契约(δ,w),零售商向供应商采购q单位的产品,并向银行融资δwq用来支付预付货款,随后零售商以零售价格p=1将产品销售到需求不确定的市场;(2)在t=T时,市场需求实现,零售商获得销售收入,并偿还银行贷款和供应商的剩余货款。

图1 资金约束零售商的组合融资结构
3 最优库存与最优利率决策
用博弈论的逆向归纳法,首先考虑零售商在给定信用契约下的库存决策及银行利率决策,再考虑供应商的最优信用契约设计。需求实现后,零售商的利润为:
πR=
(3)
记ys≜yb+(1-δ)wq。(3)式说明,当需求量小于ys时,零售商需要将所得的销售收入用来偿还银行贷款或者供应商的货款,此时零售商利润为零;然而当需求量高于ys时,零售商能够偿清全部贷款,此时零售商会有净利润 min{X,q}-ys,因此临界值ys表示零售商能够偿还所有贷款所需的最低市场需求水平。注意到(3)式等价于πR=[min{X,q}-ys]+,对其求期望,得到零售商的期望利润如下:
(4)

(5)
需要说明的是,从等式(5)与等式ys=yb+(1-δ)wq可以发现,参数(δ,w)和参数(ys,yb)是一一对应的关系,如下面引理1。
引理1:参数(δ,w)和参数(ys,yb)是一一对应的,具体对应关系如下:
(6)
引理1刻画了参数(δ,w)和参数(ys,yb)之间一一对应的关系,在后文中,我们发现求解参数(ys,yb)更为方便,因此除特殊说明,下文中用参数(ys,yb)刻画信用契约。当最优参数(ys,yb)确定后,基于式(6),参数(δ,w)即可确定。特别地,当yb=0时,有δ=0,说明供应商向零售商提供全额的信用,从而零售商的融资结构中只有交易信用融资;当ys=yb时,有δ=1,说明供应商不会向零售商提供信用,从而零售商的融资结构中只有银行融资;当ys>yb>0时,有0<δ<1,说明供应商向零售商提供部分信用,从而零售商的融资结构中既有银行融资又有交易信用融资。
定理1假设市场需求分布符合失效率递增的性质,给定信用契约(ys,yb),
(1)零售商的最优订货量q*满足下列方程:
(7)


4 考虑风险规避的最优信用契约
供应商的利润依赖于市场需求的实现值,如果市场需求低于yb,供应商只能得到零售商的预付款;如果市场需求处于yb与ys之间,除了预付款,供应商还可得到部分的延期付款;如果市场需求大于ys,供应商能够得到全部的货款,因此供应商的利润可表示为:
(8)
进一步,容易发现式(8)等价于:
πS=(δw-c)q+min{X,ys}-min{X,yb}
(9)
损失规避的供应商在设计信用契约时,需要做权衡:若要求零售商预付较多,零售商可能会降低订货量,从而影响供应商的期望收益;但若要求零售商预付较少,虽然零售商会增大订货量,但是增加了供应商无法回收剩余货款的风险。下面引理2给出了供应商的效用函数形式。
引理2:记临界值yL≜(c-δw)q+yb,
(1)当δw-c≥0时,供应商的期望效用为,
E(u(πS))=E(πS)
(2)当δw-c<0时,供应商的期望效用为,
为了便于比较与区分,在下文中称情形δw-c≥0即δ≥c/w为银行融资比例较大情形;称情形δw-c<0即δ 供应商需要确定最优的(ys,yb)使得期望效用达到最大,同时满足下列不等式约束条件(10): (10) 问题(P1)是一个二元非线性最优化问题,其中供应商的期望效用表达式由式(1)与式(9)简化而来;第一个约束条件为银行融资比例约束,等价于δwq-cq≥0,其中q由式(7)确定;第二个约束条件为临界需求水平约束,意味着能够偿还供应商剩余货款的最低需求水平不低于能够偿还银行贷款的最低需求水平,特别地,ys=yb意味着零售商全部选择银行融资。 (11) 实践中,企业的融资渠道往往是多源的,具体融资方式的选择依赖于资金约束企业自身的特点以及债权人的特点。然而,目前在供应链融资领域对单源性融资的理论研究较多,如延期付款融资、银行融资以及预付款融资,将两种融资方式混合在一起进而探讨组合融资策略下企业的最优决策的理论研究目前较少。定理2给出了组合融资策略下,债权人(即供应商和银行)以及债务人(即零售商)的最优决策。因此,定理2为资金约束企业在组合融资策略下的最优化决策提供了定量化指导。 根据引理2,此种情形下,供应商的效用函数如下: (12) (13) (14) 通过比较两种契约下供应商的期望效用,可以得到供应商的最优信用契约决策,如下定理4。 (15) 考虑到解析表达式的复杂性,本节主要用数值算例分析供应商的风险规避程度与生产成本对交易信用契约及供应链绩效的影响。 图2 最优信用契约与(λ,c)的关系 图3 最优融资结构与(λ,c)的关系 表1 供应商的风险规避程度对最优决策及供应链绩效的影响 从表1可以看出:给定生产成本c,当供应商的风险规避程度低于某个临界值时,供应商不要求零售商预付款,此时供应商会把批发价设为1;当供应商的风险规避程度高于该临界值时,零售商必须提前支付一定比例的货款,该比例与供应商的单位生产成本有关。这些结论与直觉也是一致的,因为供应商风险规避程度越强,其越希望零售商能够提前支付更多的货款,导致零售商必须向银行融资更多。进一步可发现,风险规避环境下的最优批发价不高于风险中性环境下的最优批发价,即w*|λ>1≤w*|λ=1;风险规避环境下的银行融资比例不低于风险中性环境下的银行融资比例,即δ*|λ>1≥δ*|λ=1;风险规避环境下的最优订货量不高于风险中性环境下的最优订货量,即q*|λ>1 给定供应商的风险规避系数,由表1可发现,在零售商的组合融资结构中,供应商的单位生产成本越高,零售商的银行融资比例越大,对应的批发价也越高,供应商的期望效用越低。这是因为较高的生产成本导致供应商面临较大的损失风险,迫使供应商设定较高的批发价,导致零售商没有动力订更多的产品,最终影响到供应商的收益。另一方面,银行融资比例δ*关于单位成本c是递减的,说明供应商的生产成本越高,其越倾向与银行共同承担需求不确定的风险。 学术界在研究供应链融资问题时一般较少考虑债权人的风险规避性问题,同时债务人的融资结构设计在供应链融资领域也较少提及。本文针对供应链的资金约束问题,考虑了风险规避型供应商如何通过设计最优的信用契约影响资金约束零售商的融资结构。研究发现,供应商的风险规避程度对最优信用契约及对应的融资结构有很大的影响,当供应商的风险规避程度低于某个临界值时,供应商偏好设计一个单一的交易信用契约;而当供应商的风险规避程度高于该临界值时,供应商偏好设计一个组合信用契约,从而零售商的融资结构从单一的交易信用融资转移到组合融资。除此之外,供应商的生产成本也会影响到最优信用契约,供应商的生产越大,组合融资中的银行融资比例也越大。 本文主要从供应商角度研究风险规避程度对最优信用契约的影响,由此衍生出了资金约束零售商的最优融资结构。为了简化分析,文中假设零售商是非策略型的,即零售商只根据设计好的信用契约确定最优库存,而对融资比例没有决策权。未来可研究策略性零售商在面临多融资渠道环境下的组合融资问题。 附录 引理1的证明: 基于等式(5)以及等式ys=yb+(1-δ)wq即可得到。 证毕 定理1的证明: 注意到δwq(1+r) E[min{X,δwq(1+r)}]=δwq (A1) 记yb=δwq(1+r),考虑到对于任意的a∈,成立因此(A1)进一步等价于 (A2) (A3) (A4) 结合式(A3)和式(A4)并利用一阶必要条件,可得q满足下列等式(即表达式(7)), 证毕 引理2的证明: 由表达式(8)发现,当δw-c≥0时,πS>0恒成立。由此,基于供应商的损失效用函数的定义(即表达式(2)),可得u(πs)=πs,从而E(u(πS))=E(πS)。当δw-c<0时,令yL≜(c-δw)q+yb,则由表达式(8)发现,当X>yL时,πS>0;否则πS≤0。类似地,基于供应商的损失效用函数的定义(即表达式(2)),可得 (A5) 证毕 定理2的证明: 证明 构造Lagrange 函数 对L(ys,yb,u1,u2)分别关于ys,yb,u1和u2求一阶偏导数,得到: (A6) 可以写出KKT条件,即: (A7) 1)u1>0和u2=0。 此时,根据式(A1)和式(A2),我们有: (A8) (A9) 对式(7)两边分别关于ys和yb求偏导,得到 (A10) 结合式(A10)并对式(A9)整理得到, 2)u1=0和u2>0。 下面说明该情形不可能存在,用反正法。假设u1=0和u2>0成立,则根据KKT条件(即式(A7))有: 综上,只有情形1)存在,情形1)下的最优解即为(P1)问题的最优解。 证毕 定理3的证明: 构造Lagrange 函数 (A11) 对V(ys,yb,υ1,υ2)分别关于ys,yb,v1和v2求一阶偏导数,得到: 可以写出KKT条件,即: (A12) 证毕 定理4的证明: (A13) (A14) [1] Seifert D, Seifert R W, Protopappa-Sieke M. A review of trade credit literature: Opportunities for research in operations [J]. European Journal of Operational Research, 2013, 231(2): 245-256. [2] Thangam A. Optimal price discounting and lot-sizing policies for perishable items in a supplychain under advance payment scheme and two-echelon trade credits[J]. International Journal of Production Economics, 2012, 139(2): 459-472. [3] Zhang Qinhong, Dong Ming, Luo Jianwen, et al. Supply chain coordination with trade credit and quantity discount incorporating default risk [J]. International Journal of Production Economics, 2014, 153: 352-360. [4] Buzacott J A, Zhang R Q. Inventory management with asset-based financing [J].Management Science, 2004, 50 (9): 1274-1292. [5] Xu Xiaodong, Birge J R. Joint production and financing decisions: Modeling and analysis [R].Chicago: University of Chicago, 2004. [6] Dada M, Hu Qiaohai. Financing newsvendor inventory [J].Operations Research Letters, 2008, 36(5): 569-573. [7] Lai Guoming, Debo L G, Sycara K. Sharing inventory risk in supply chain: The implication of financial constraint [J]. Omega, 2009, 37:811-825. [8] Kouvelis P, Zhao Wenhui. The Newsvendor Problem and Price-Only Contract When Bankruptcy Costs Exist [J]. Production and Operations Management, 2011, 20(6): 921-936. [9] 易雪辉, 周宗放. 基于供应链金融的银行贷款价值比研究[J]. 中国管理科学, 2012, 20(1): 102-108. [10] 王文利, 骆建文, 张钦红. 银行风险控制下的供应链订单融资策略研究[J]. 中国管 理科学, 2013, 21(3): 71-78. [11] Schwartz R A. An economic model of trade credit [J]. Journal of Financial and Quantitativeanalysis, 1974, 9(4): 643-657. [12] Petersen M A, Rajan R G. Trade credit: Theories and evidence [J].Review of financial studies, 1997, 10(3): 661-691. [13] Burkart M, Ellingsen T. In-kind finance: A theory of trade credit [J]. American Economic Review, 2004, 94(3): 569-590. [14] Jamal A M M,Sarker B R,Wang shaojun.On optimal payment time for a retailer under permitted delay of payment by the wholesaler [J].International Journal of Production Economics, 2000, 66(1):59-66. [15] 朱文贵, 朱道立, 徐最. 延迟支付方式下的存货质押融资服务定价模型[J]. 系统工程理论与实践, 2007, 27(12):1-7. [16] Shi Xiaojun, Zhang Shuanming. An incentive-compatible solution for trade credit term incorporating default risk[J]. European Journal of Operational Research, 2010, 206(1): 178-196. [17] 陈祥锋. 资金约束供应链中贸易信用合同的决策与价值[J]. 管理科学学报, 2013, 16(12): 13-20. [18] Yang S A, Birge J R. How inventory is (should be) financed: Trade credit in supply chains with demand uncertainty and costs of financial distress [R]. Chicago: University of Chicago, 2013. [19] 王文利, 骆建文. 交易信用与资金约束下两阶段零售商订货策略[J]. 系统工程理论与实践, 2014, 34(2): 304-312. [20] Kouvelis P, Zhao Wenhui. Financing the newsvendor: supplier vs. bank, and the structure of optimal trade credit contracts[J].Operations Research, 2012, 60(3): 566-580. [21] Jing Bing, Chen Xiangfeng, Cai Gangshu. Equilibrium financing in a distribution channel with capital constraint [J].Production and Operations Management, 2012, 21(6): 1090-1101. [22] Cai Gangshu, Chen Xiangfeng, Xiao Zhiguo. The roles of bank and trade credits: Theoretical analysis and empirical evidence [J].Production and Operations Management, 2014, 23(4): 583-598. [23] Chen Xiangfeng. A model of trade credit in a capital-constrained distribution channel [J]. International Journal of Production Economics, 2015, 159: 347-357. [24] Schweitzer M E, Cachon G P. Decision bias in the newsvendor problem with a known demand distribution: Experimental evidence [J].Management Science, 2000, 46(3): 404-420. [25] Wang C X, Webster S. Channel coordination for a supply chain with a risk-neutral manufacturer and a loss-averse retailer[J]. Decision Sciences, 2007, 38(3): 361-389. [26] Wang C X, Webster S. The loss-averse newsvendor problem [J].Omega, 2009, 37(1): 93-105. [27] 马利军, 葛羊亮, 薛巍立, 等. 不确定环境下损失规避零售商的提前支付决策[J]. 系统工程理论实践, 2015, 35(2):315-323. [28] 王佳, 金秀, 苑莹, 等. 基于损失规避和模糊规避的分布鲁棒投资组合模型[J]. 系统工程理论与实践, 2016, 36(2): 288-296. [29] Lariviere M A, Porteus E L. Selling to the newsvendor: An analysis of price-only contracts[J]. Manufacturing & service operations management, 2001, 3(4): 293-305. [30] Caldentey R, Chen Xiangfeng.Handbook of integrated risk manfment in global supply Chain. The role of financial services in procurement contracts[M].Hoboken,New Jersey:John Wiley & Sons,2007.4.1 银行融资比例较大情形


4.2 银行融资比例较小情形


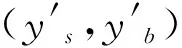
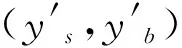
4.3 最优信用契约与最优融资结构




5 数值分析




6 结语