LEVY-LIBOR市场模型的蒙特卡罗模拟参数校准与估计
2018-03-09刘凤琴
刘凤琴,金 瑜
(浙江财经大学,浙江 杭州 310018)
1 引言
随着LIBOR作为国际货币市场基础利率体系的作用愈加凸显,以LIBOR为标的变量的各种利率衍生证券得以大量产生;因此,建立科学合理的LIBOR利率动态期限结构模型也就引起更多学者关注。Rutkowski[1]利用测度变换公式得出在远期测度Qk下,有限个远期LIBOR利率Li(t)服从的随机过程,建立了标准化LIBOR市场模型,但模型假设隐含波动率为常数,无法体现可观察市场隐含波动率所具有的波动率偏斜或者微笑等特征;尤其是近些年来,由于金融市场不确定性程度不断增加,金融危机等突发性事件发生愈加频繁,LIBOR利率也呈现出更加明显随机波动和急剧跳跃特征;因此,建立具有Levy跳跃和随机波动特征的LIBOR市场模型则成为LIBOR动态期限结构研究重要内容。
近些年来,国内外学者在相关领域研究主要集中在两个方面:一是引入随机波动率和跳跃扩散过程,对标准化LIBOR市场模型进行结构性扩展;二是寻找一些适当方法对这些模型进行有效参数校准估计。主要研究文献包括:Joshi等[2]最早提出随机波动率LIBOR市场模型,模型假设瞬时远期利率波动率服从Ornstein-Uhlenbeck过程,此即所谓Heston随机波动率模型(Heston-LMM);Hagan等[3]将SABR模型引入LIBOR过程中形成SABR-LMM。Glasserman等[4]假设利率服从对数正态分布,并采用不同平均跳跃幅度来拟合波动率变化特征,推导出了利率上限期权和利率互换期权的封闭解。Elliott等[5]提出一种机制转换随机波动率LIBOR市场模型,瞬时远期LIBOR波动率服从连续时间马尔科夫链,同时波动率参数服从机制转换性质的平方根过程。Andersen等[6]在LMM的基础上引入具有均值回复特征的随机波动率过程,并运用近似扩展技术推出利率上限期权和互换期权定价封闭解。Eberlein等[7]首次将Levy跳跃过程引入标准LIBOR市场模型,并借助双向拉普拉斯变换导出利率上限、利率下限的精确定价公式。Eberlein等[8]在Levy-LMM的基础上,以交叉货币期权为研究对象,推导出定价交叉货币衍生产品公式,并运用双向拉普拉斯转换来进行数值计算。刘志东和陈晓静[9]在对经典的和修正的Levy tempered stable 分布进行研究的基础上,结合现实中金融资产收益分布的实际特征,分析Levy tempered stable 分布在构建模拟金融资产价格过程的Levy J ump 模型的优势。Belomestny等[10]提出跳跃扩散LIBOR市场模型,并且检测了一个将局部协方差结构考虑在内的稳定非参数校准算法,不仅能够反映市场中突然跳跃行为,而且能够成功地捕捉到利率衍生品市场中隐含波动率曲面的非厚尾特征。Ebelrein等[11]在LIBOR市场模型条件下考虑对信用风险进行建模,构建了以评级为基础的LIBOR市场模型,并将时间非齐次Levy过程作为无违约和有违约前的LIBOR随机过程。Ferreiro[12]将SABR模型与LIBOR市场模型相结合来捕捉市场中的波动率微笑和偏斜,提出一个与模拟退火算法类似的GPU集群并行技术来对模型进行校准。Leippold和Strmberg[13]对于利率上限期权和利率互换期权联合定价提出了一种全时变Levy-LMM,充分考虑了金融危机对利率动态变化影响,更加准确地捕捉利率市场中随机性和跳跃特征。鲍杰和葛静[14]在最小卡方估计方法基础上研究了高斯仿射利率模型的参数识别和估计问题,以标准化高斯模型为起点,从结构化模型和简约化模型参数的函数关系出发研究高斯仿射模型的可识别性。刘志东等[15]采用CGMY和GIG过程对非高斯OU随机波动率模型进行扩展,建立连续叠加Levy过程驱动的非高斯OU随机波动率模型,并给出模型的散粒噪声(Shot-Noise)表现方式与近似。
虽然LIBOR市场模型研究已取得许多进展,但仍然存在一定局限,主要包括两方面:一是模型建立,大多数文献建立单因子非标准化LIBOR市场模型,针对levy过程和随机波动率有机融合方面还缺乏系统研究。二是模型参数校准估计,大都采用传统估计方法,在非标准化LIBOR市场模型模型参应用中存在一定局限性。本文首先将随机波动率和levy跳跃同时引入,建立多因子非标准化LIBOR市场模型;在此基础上,运用非参数化相关矩阵蒙特卡罗模拟和自适应MCMC,对模型参数进行有效市场校准估计。主要内容包括五个部分:第一部分为引言,第二部分非标准化LIBOR市场模型的建立,第三部分为模型参数的市场校准方法,第四部分为模型的参数估计;最后为结束语。
2 理论模型的结构性扩展
2.1 随机波动率LIBOR市场模型局限
图1中是6种有不同到期日利率上限隐含波动率平值报价,隐含波动率在2010年前后波动非常剧烈,在2007年前一段时间内波动较为平缓,而标准LIBOR市场模型无法提供完全解释。随机波动率模型主要用于刻画市场波动率微笑和偏斜等特征。考虑到均值回复特征和解释波动率偏斜等特征,很多学者都采用了Heston随机波动率模型对LIBOR标准市场模型进行扩展(LMM-SV)。Heston随机波动率模型下的欧式期权可导出显式解析解,而且使其可在某些情况下很好解释波动率集聚、长记忆性和隐含波动率的偏斜效应等,相比其他SV模型得到了更广泛应用;但Heston模型不能生成跳过程,Heston-LMM模型无法对短期内标资产剧烈波动提供很好解释。而且Rebonato和White(2009)[16]认为当标的资产的存续期较长时,Heston-LMM模型无法重现波动率微笑特征,从而也无法提供对波动率微笑的有效解释。
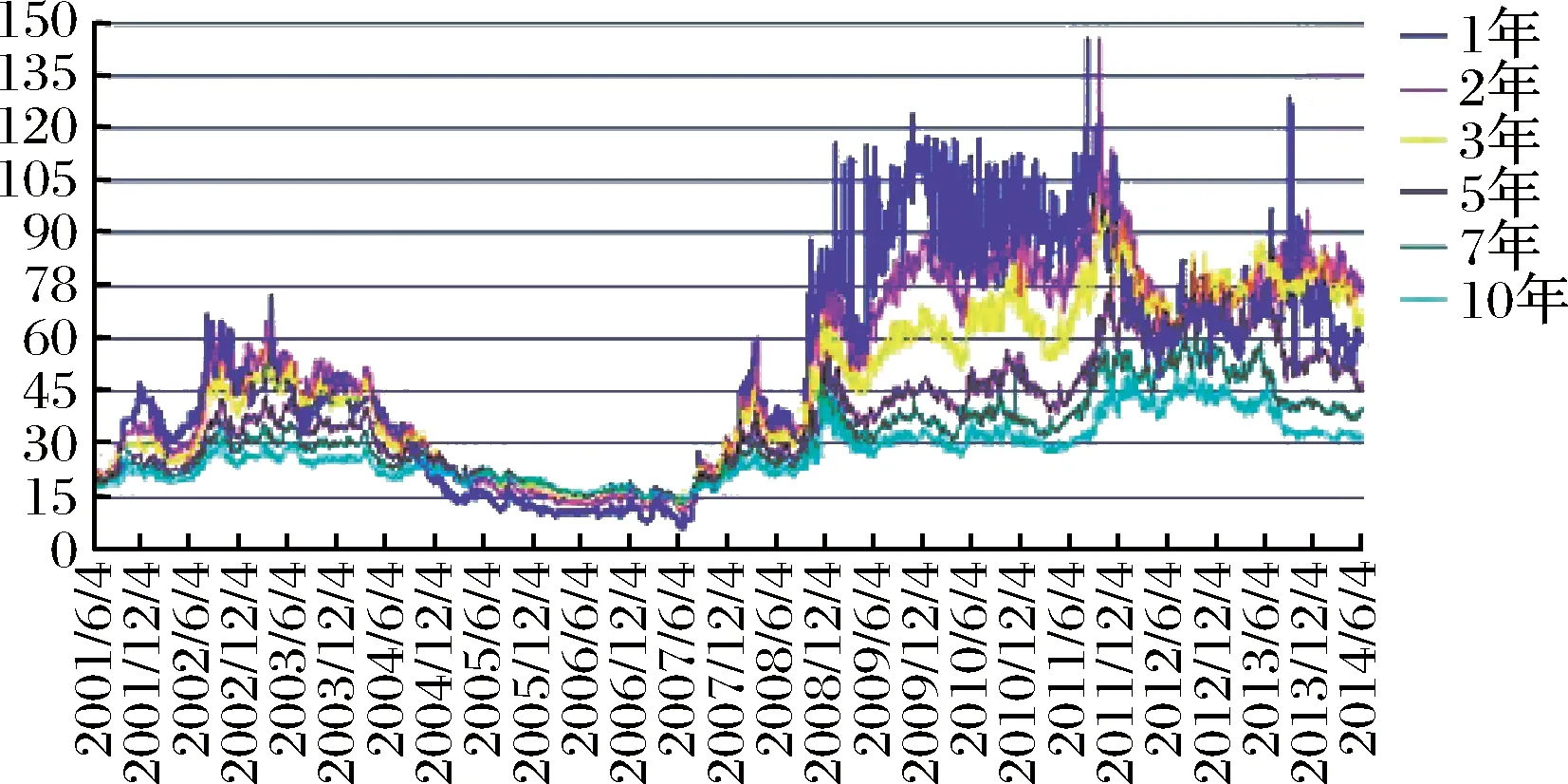
图1 利率上限隐含波动率的平值报价
2.2 理论模型选择与确定
(1)模型组成框架
本文在此考虑将跳跃扩散现象和随机波动率一起引入,建立更为有效的非标准化LIBOR市场模型。进一步分析认为, LIBOR利率集聚跳跃出现了一些新特征,即经常会在有限时间内发生充分多次数次跳跃,因而诸如Piosson跳跃等传统模型很难刻画。为此,将考虑运用Levy跳跃过程建立Levy-LIBOR市场模型(SVLEVY-LMM)。基本框架为:
1)在远期测度Qk下,SVLEVY-LMM模型为:
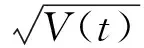
(1)
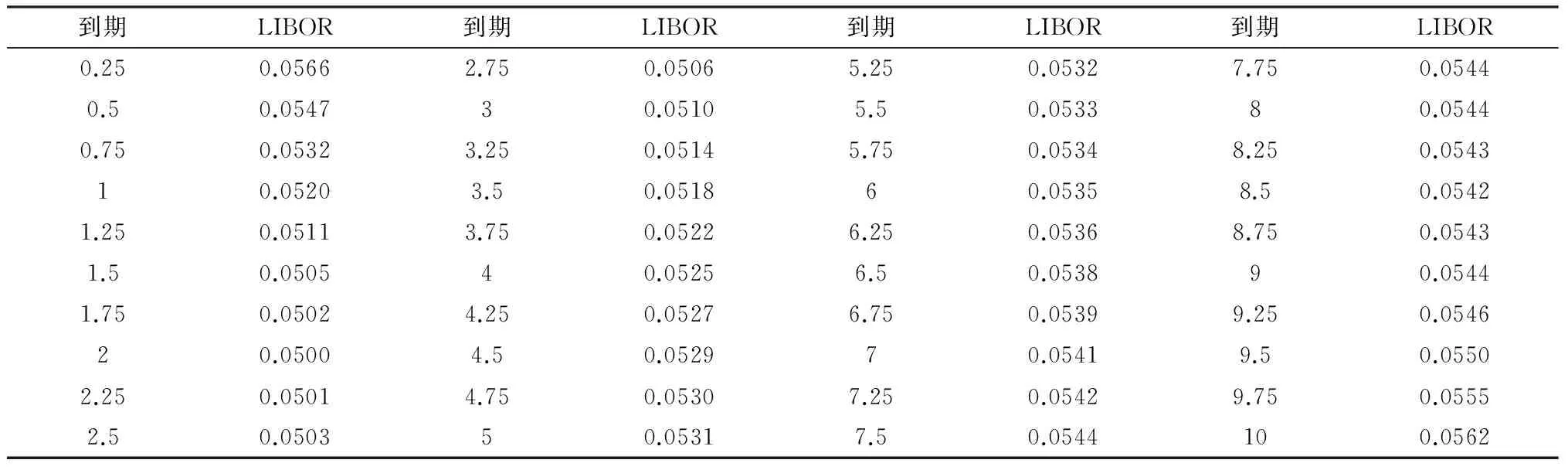
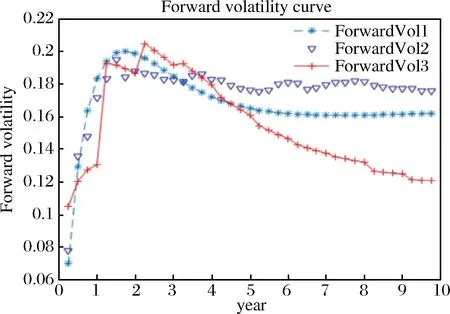
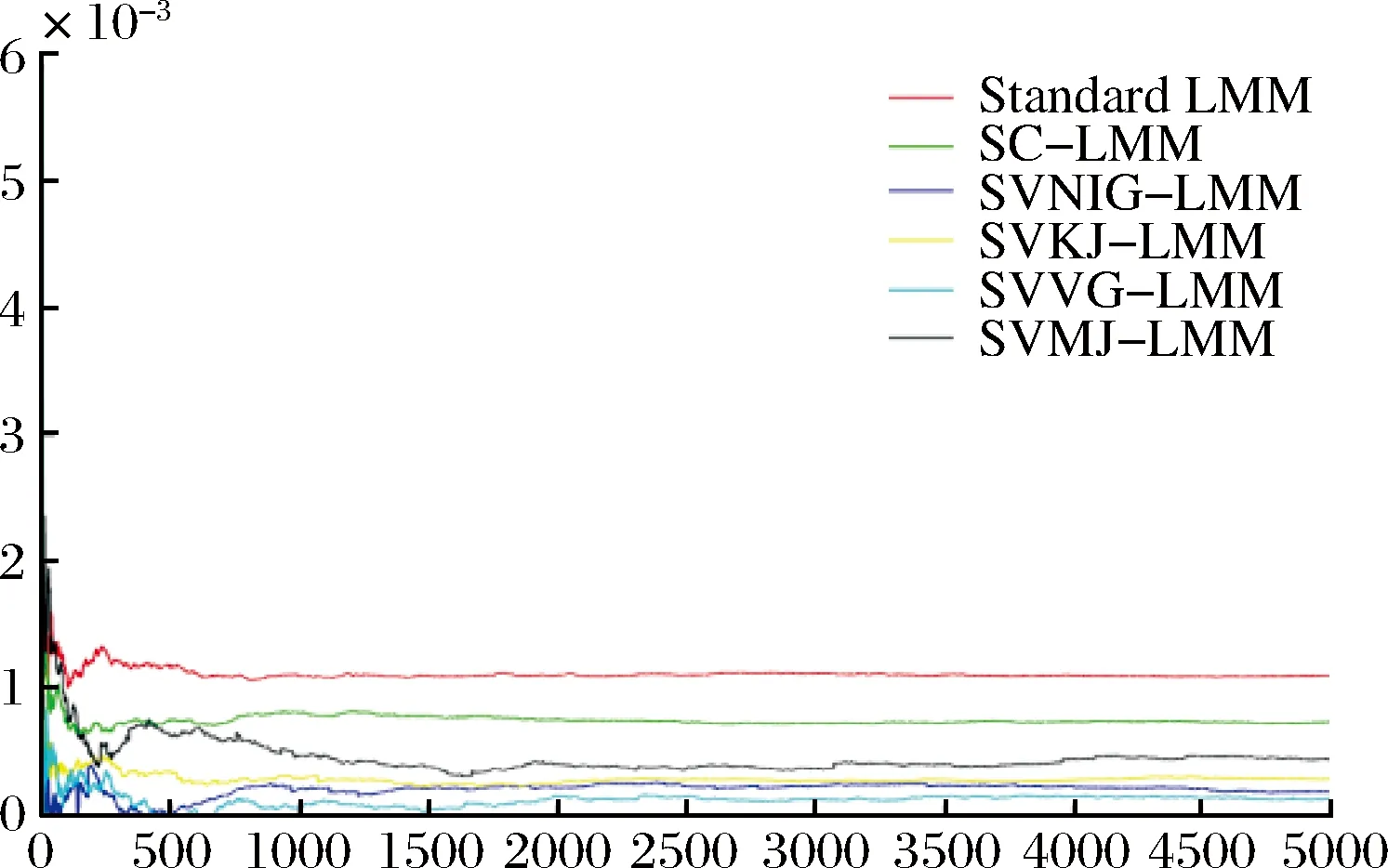
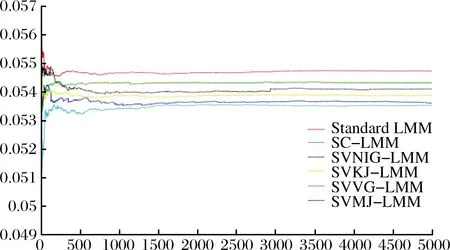
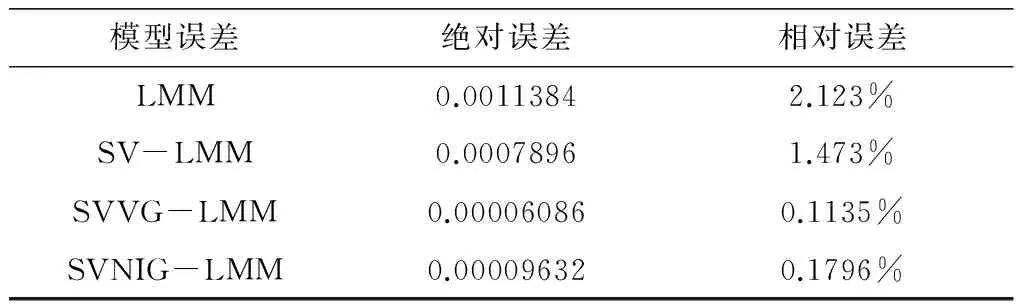
2)在远期测度Qj(Tj dωk(t)dW(t)=ρdt (2) 3)在远期测度Qj(Tj>Tk)下,SVLEVY-LMM市场模型为: (3) (2)模型的两种具体类型 Levy跳跃主要包括有限活动跳跃和无限活动跳跃两种类型,本文主要针对正态逆高斯(简记NIG)和方差伽马(简记VG)两类常见无限跳跃Levy过程加以分析。 (4) 市场校准就是在模型基准参数集基础上,将市场信息纳入考虑范围,进行模型参数估计的过程。远期LIBOR利率动态过程由利率波动率γk(t)和利率间的相关系数矩阵ρk.i两个重要参数决定;其中,波动率γk(t)决定了各个远期利率在不同时点波动率,ρk.i则决定了各个远期利率相关系数。因此,LMM校准就是通过精确估计这两个参数使模型导出的利率衍生品价格和市场报价尽可能接近。 (1)瞬时波动率结构的基本类型 远期LIBOR利率过程扩散式σi(t):[0,Tn+1]→Rd为远期LIBOR的瞬时波动率,可被分解为:σi(t)=γi(t)ei(t) ,ei∈Rd;其中,ei为一组单位向量;γi:[0,Tn+1]→R+i=1,2,....,M。只有γi影响利率上限单元(caplet)价格而ei确定相关系数结构。利率波动率结构可表示为四种形态,本文基于实证结论及计算简便对前两种形态进行分析,(参看Belomestny和Schoenmakers[10]。 1) 分段常数瞬时波动率结构。假设远期利率的波动率随着区间(Ti-1,Ti)不同而有所差异,区间内则维持不变,表示为:σk(t)=σk,η(t),(η(t)是t后第一个利率支付期),M个波动率结构见由表1: 2) 到期日依赖波动率结构。假设远期利率波动率只受到期期限影响, 数学表示为σk(t)=σk-(η(t)-1)(η(t)是时间t之后的第一个利率支付期),如表2说明。 表1 远期LIBOR利率波动率结构σk,ηt 表2 远期LIBOR利率波动率结构σk-(η(t)-1) (2)波动率的市场校准过程 1)前期准备。一般地在市场上仅能获取LIBOR利率都是1年以内即期利率,而通常则需要模拟远期LIBOR利率大多为1年以上。常见做法是利用当前即期利率和互换利率推导出远期利率;由于并非所有期限的互换利率都能在市场上获取,所以需要利用非线性插补法补齐,得到光滑期初远期互换曲线;然后利用公式(5)计算零息债券价格,并获得期初远期LIBOR利率。 (5) 2)远期LIBOR利率瞬时波动率校准。Caplet隐含波动率完全依赖于第i期远期LIBOR利率瞬时波动率,但Caplet报价无法在市场上直接观察,所以可利用市场上平价(ATM)利率上限。市场上利率上限一般为波动率报价,而利率上限可视为一组拥有同一利率上限单一隐含波动率报价的欧式Caplet总和。可运用公式(6)得到t=0利率上限单一隐含波动率和利率上限元即期隐含波动率: (6) LIBOR相关系数矩阵除了一般相关矩阵特征,还需要满足去相关性和等间隔相互依赖性随间隔增加而增加两个特殊性质。因此,对其校准具有一定复杂性。目前,LIBOR市场模型参数校准方法主要包括两类:一是Rebonato’s逼近的联合校准方法(可参考Rebonato[16],二是蒙特卡罗模拟校准参数化相关性矩阵方法。本文将蒙特卡罗模拟校准扩展到非参数化相关性矩阵,构建采取非终期相关系数随机从[0,1]区间内抽取,终期相关系数则结合相应波动率结构分别导出,步骤为: (1)模型离散化方法 常用欧拉离散化方法实质上是对随机过程中的随机积分采用一阶化逼近,因此针对远期LIBOR市场模型常会产生一定偏差。为此,采用具有二阶逼近特征的米尔斯坦离散化方法,形式如式为: 而终期相关系数通过式(7): (7) (8) (4)对于非终期相关系数,求解如下的等式约束最优化问题: (9) (5)获得终期相关系数。 运用2006年9月15日为起始日的市场数据进行实证分析。首先,构建期初远期LIBOR利率;然后,计算Caplet波动率和远期LIBOR利率瞬时波动率以及相关系数。 (1)期初远期LIBOR利率构建 利用市场上流动性最好的互换利率和LIBOR利率构建远期LIBOR利率曲线。互换利率如表3: 表3 期初远期互换利率 资料来源:Bloomberg ICAU报价系统(2006/09/15) 利用非线性插值法得到以3月期互换利率,期初零息债券价格可由(10)求得: (10) 市场只有1年内LIBOR利率报价如表4。对于1年以上债券价格,则公式(6)得到。结果如表5: 表4 期初LIBOR利率 资料来源:Bloomberg ICAU报价系统(2006/09/15) 表5 10年期初各到期日的零息债券价格 然后利用(10),求出相应期初LIBOR远期利率,如表6所示。 (10) (2)远期LIBOR利率瞬时波动率的校准 据此计算各远期利率波动率,再获取caplet隐含波动率期限结构,即: 表6 期初远期LIBOR利率 表7 Cap波动率报价 资料来源:Bloomberg ICAU报价系统(2006/09/15) 最后,利用公式(11)和不同瞬时波动率假设,得到远期LIBOR利率瞬时波动率曲线(图2)。ForwardVol1代表分段固定波动率结构,ForwardVol2代表到期日依赖波动率结构,ForwardVol3代表常数波动率结构。一般地,结果较好波动率表现为平滑而稳定的波动率期限结构。由图2,分段固定波动率结构校准结果较好。再使用校准误差对校准生成相关系数矩阵进行比较分析,校准误差由(11)计算。三种不同校准方法误差与时间评价如表8。可知,方法1使用Rebonato提出的校准方法需要计算时间最短,但校准结果不尽如人意;方法2利用参数化相关系数矩阵进行校准,需要最长模拟时间;方法3基本满足了相关系数矩阵特征,具有最小估计误差和最好市场适应性。 (11) 图2 期初远期LIBOR利率瞬时波动率曲线 校准方法平均校准时间平均校准误差Rebonato’s校准法6min,13sec8.34%蒙特卡罗模拟的参数化相关系数矩阵17min,45sec3.16%蒙特卡罗模拟的非参数化相关系数矩阵15min,32sec0.732% 由于SVLEVY-LMM复杂性程度不断提高,MCMC得到广泛应用。但MCMC的Metropolis-Hastings算法(M-H)和Gibbs抽样,对于超高维空间数据较难构建具有良好收敛特性的转移概率核。考虑到LIBOR扩展模型涉及到高维联合概率分布,运用一种新的自适应M-H抽样算法来加以实现,建议分布根据抽样过程中获得目标分布的点进行实时调整。假设点X1,X2,...Xk已经抽样,候选点Y通过建议分布qk(·|X1,X2,...,Xk)抽样得到,建议分布依赖过去抽样得到信息适时调整[17]。 一般地,米尔斯坦离散化方法具有更好的模拟效果。但是由于模型包含了随机波动率和levy两类扩展,在运用该方法时将会遇到计算处理方面困难;因此,考虑运用欧拉离散化方法加以实现。 (1)模型一般离散化框架 (12) (2)两种随机波动率Levy-LIBOR模型的离散化 1)方差伽马跳跃过程(VG) ,模型的离散化形式可表示为: (13) 2)正态逆高斯过程(SVNIG),模型的离散化形式可表示为: (14) 在此,以SVVG模型为例加以说明,波动率状态变量ht的联合后验分布可表示为: p(ht|ht-Δ,ht+Δ,Θ,x)∝ p(ht|ht-Δ,Θ)p(ht+△|ht,Θ)p(xt|ht,Θ) 利用自适应M-H进行抽样,先初始化参数集合Θ0和h0,MCMC算法步骤: (8)利用并行化自适应M-H算法,从p(ht|ht-Δ,ht+Δ,Θ,x)抽取ht,具体步骤: 1)设置ht的初始值h0;2)设建议分布为N(ht-Δ,Ct),利用随机游走M-H抽样算法生成K条并行独立马尔科夫(MC)链;3) 分别计算各条MC链接受新状态比例,设为qt;4) 分别生成qt判断,若qt落入[a-ε,a+ε]内,则h=ht,退出;若qt∉[a-ε,a+ε],则转入下一步;5)若t>2,且|qt-a|<|qt-1-a|,则置h=ht-Δ;6)在单独MC链上,分别对建议分布方差进行调整,利用MC链建议分布生成新建议分布,反馈于运行马尔科夫链;然后利用新生成值作为初始值反复迭代,更新参数,迭代m次。 (1)数据选择 2006年9月15日为分界点,假设Δ=1/360,t=0,F1(0)、F1(0+Δ)、F1(0+2Δ)...,F1(0+90Δ)为估计需要数据。 表9 各计息日下的远期LIBOR利率 (2)模型参数估计结果 首先需要讨论参数先验分布假设问题。由遍历性定理可知,平稳分布与初始分布时没有直接关系, t时点状态只与t-1时点状态有关;当经过迭代后,各个状态边际分布都成平稳分布时,就称该马尔科夫链收敛。所以,为了计算简单,在此采用Mikkelsen P[18]所提出的设置方式。 表10 SVVG模型各参数估计值及相关统计数据 计算:ξ=1.1805;κ=5.9292;θ=0.1237;θVG=-0.03162;σVG=0.3861;ϑVG=0.0025;模型变为: 其中,由Gt~Γ(t/ϑVG,1/ϑVG),得Gt~Γ(400t,400)。 Γ(5,0.5),βNIG~U(-3,3),设φ=kΔ;a=kθΔ;Δ=1/360;φ~β(2.5,150),a~β(2,1000),1/τ2~Γ(0.4,1.3);迭代2万次,模型各参数统计数据如表11所示。 表11 SVNIG模型各参数估计值及相关统计数据 计算得:ξ=1.3659;κ=5.155;θ=0.1465;αNIG=2.116;βNIG=-0.07542;δNIG=0.1781;模型为: 由于模型随机特性,对生成路径模拟5000次,求模拟路径均值。模拟三月后远期LIBOR利率。从图3中看到,当模拟次数为5000次时,远期LIBOR利率模拟路径已经基本收敛。 为更好判断模拟效果,取模拟路径均值,计算每步平均利率与实际利率的差的平方,并取均值,计算步骤如下:1)LIBOR远期利率模拟均值:h=(F1+F2+...+Fn)/n,其中n代表模拟次数,Fk,n代表第i次的第k日模拟值。2)LIBOR远期利率的模拟绝对离差:c=abs(h-L),其中L表示真实利率,如图4。各个模型假设的蒙特卡罗模拟绝对误差和相对误差如表12。实验证明,SV-LMM比标准LMM能更精确描述远期LIBOR利率变化趋势。而与有限跳跃过程比, SVVG-LMM 和SVNIG-LMM能更好模拟远期LIBOR利率动态变化特征。 图3 远期LIBOR利率的蒙特卡罗模拟结果 图4 远期LIBOR利率绝对离差值的蒙特卡罗模拟结果 模型误差绝对误差相对误差LMM0.00113842.123%SV-LMM0.00078961.473%SVVG-LMM0.000060860.1135%SVNIG-LMM0.000096320.1796% 理论与实证研究表明,具有无限跳跃特征的Levy过程能更好模拟远期LIBOR利率动态变化特征;非参数化相关系数矩阵的蒙特卡罗模拟方法具有最好校准效果,非参数化相关系数矩阵具有最小的估计误差和最佳的市场适应性;并行化自适应MCMC方法比普通的MCMC方法具有更高的收敛效率。但是,由于模型结构较为复杂,研究内容还需在两个方面进一步完善与扩展。一是本文仅对VG和NIG两种Levy跳跃模型做了实证研究,对其他模型研究尚待进一步探讨;为计算简便,在计算中假设模型方程中两个随机过程的相关系数为0,对不相关性假设需要做进一步的改善。 [1] Rutkowski M. Models of forward Libor and swap rates[J].Applied Mathematical Finance, 1999, 6(1):29-60. [2] Joshi M, Rebonato R. A stochastic-volatility, displaced-diffusion extension of the Libor market mdel[J].Quantitative Finance,2001, 61(1):341-378. [3] Hagan P, Kumar D.Lesniewski A S,et al. Managing smile risk[J]. Wilmott, 2002(1): 84-102. [4] Glasserman P, Monte Carlo methods in financial engineering[M]. New York:Springer Verlag,2003. [5] Elliott R, Valchev S. Libor market model with regime-switching volatility[R]. Working Paper,National Centre of Competence in Research,2004. [6] Andersen L B G, Brotheton-Ratcliffe R. Extended libor market models with stochastic volatility[J]. The Journal of Computational Finance, 2005:1-40. [7] Eberlein E, özkan F. The Lévy LIBOR model [J]. Finance and Stochastics, 2005, 9(3): 327-348. [8]Eberlein E, Koval N. A cross-currency Lévy market model[J]. Quantitative Finance, 2006, 6(6): 465-480 [9] 刘志东, 陈晓静.Levy Tempered Stable金融资产收益分布及其CF-CGMM估计方法研究[J].中国管理科学,2009,17(3):18-26. [10] Belomestny D, Schoenmakers J. A jump-diffusion Libor model and its robust calibration[J]. Quantitative Finance, 2011, 11(4): 529-546. [11] Ebelrein E, Grbae Z. Credit rating based Levy LIBOR model[J]. Mathematieal Finance, 2013, (4): 591-626. [12] Ferreiro A M, Garcia-Rodriguez J A, López-Salas J G, et al. SABR/LIBOR market models: Pricing and calibration for some interest rate derivatives[J]. Applied Mathematics and Computation, 2014, 242: 65-89. [13] Leippold M, Strømberg J. Time-changed Lévy LIBOR market model: Pricing and joint estimation of the cap surface and swaption cube[J]. Journal of Financial Economics, 2014, 111(1): 224-250. [14] 鲍杰, 葛静.基于MCS方法的高斯仿射利率期限结构模型研究[J].中国管理科学,2015,23(7):10-17. [15] 刘志东, 刘雯宇. Lévy过程驱动的非高斯OU随机波动模型及其贝叶斯参数统计推断方法研究[J].中国管理科学,2015,23(8):1-9; [16] Rebonato R, Mckay K, White R. The SABR/LIBOR market model pricing, calibration and hedging for complex interest rate derivatives[M]. Hoboken,New Jersey: John Wiley & Sons,2009. [17] Brockwell A, Kadane J. Identification of regeneration times in MCMC simulation, with application to adaptive schemes [J]. Journal of Computational and Graphical Statistics, 2005, 14(2): 436-458. [18] Mikkelsen P. MCMC based estimaton of term structure models[R]. Working paper, The Aarhus School of Business, Denmark, 2002.
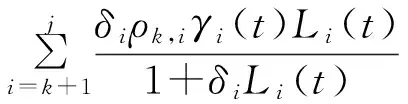
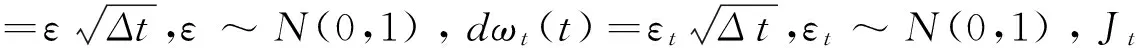
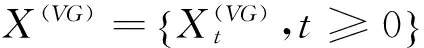
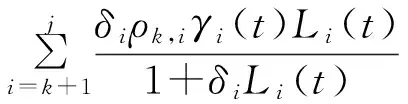
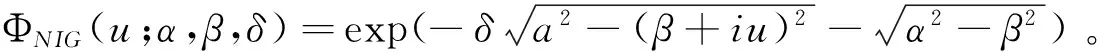

3 模型参数的市场校准
3.1 波动率期限结构及其市场校准



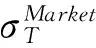
3.2 远期LIBOR利率的瞬时相关系数的校准方法
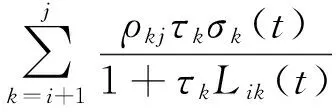
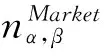
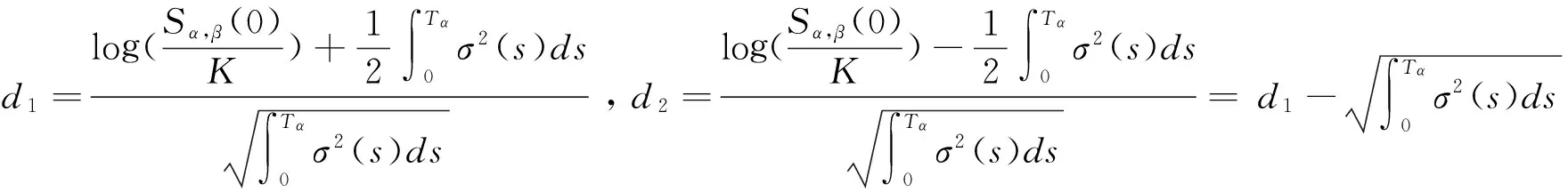
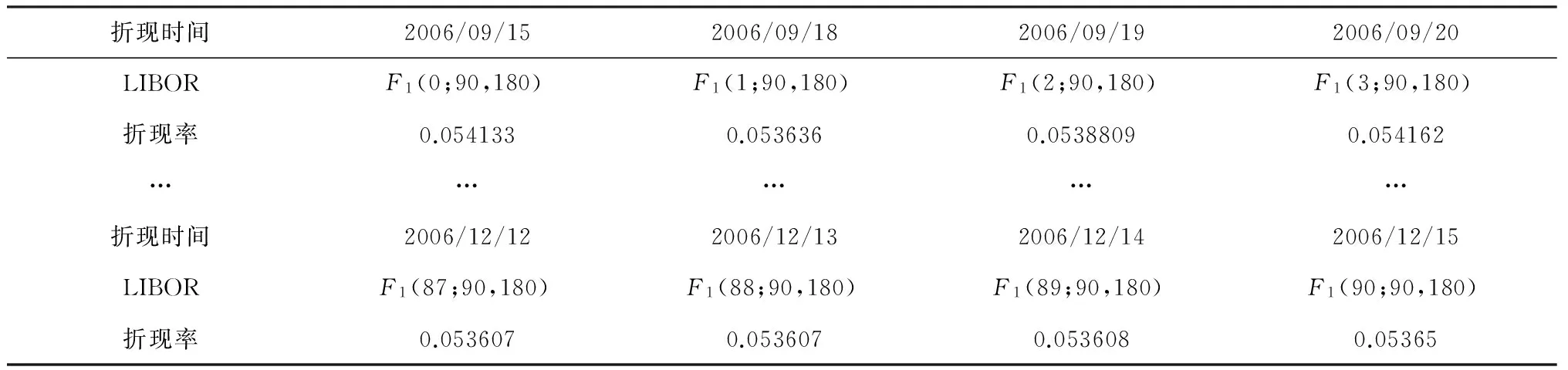
3.3 模拟计算


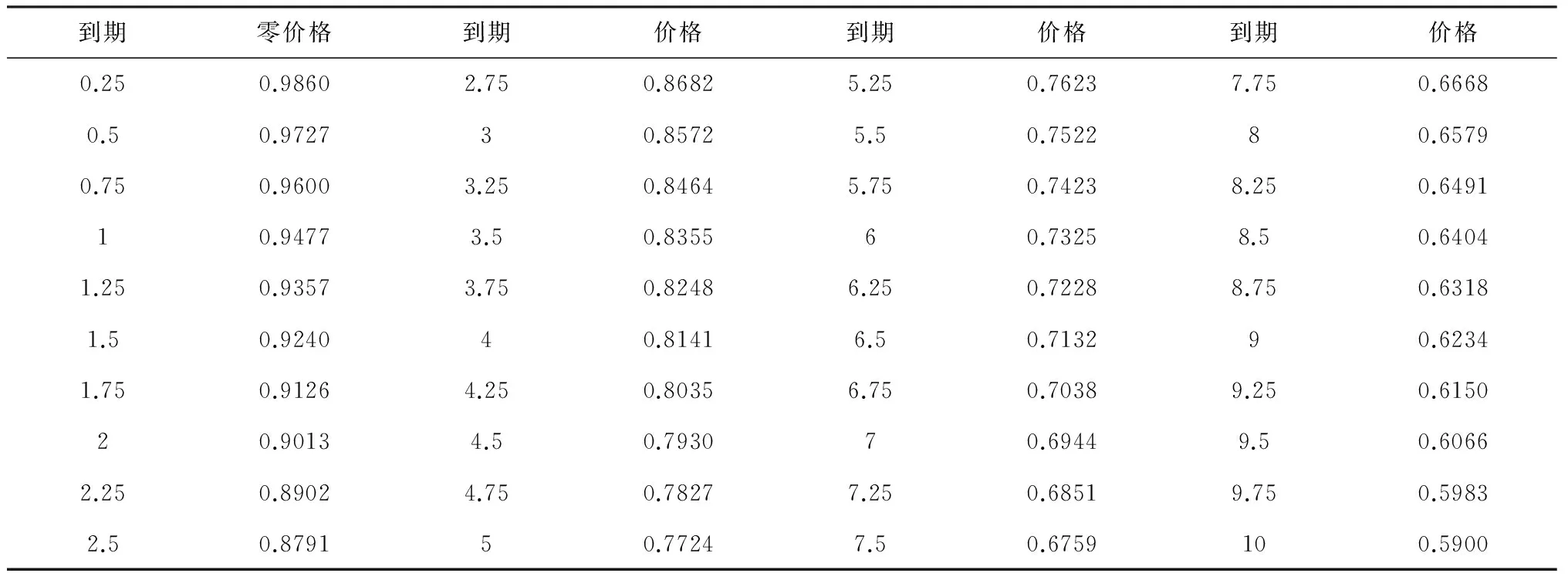
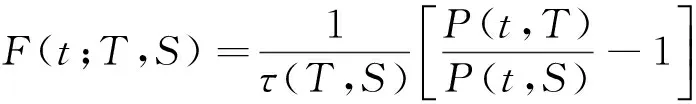



4 模型参数的自适应马尔科夫链蒙特卡罗模拟估计
4.1 模型的离散化过程
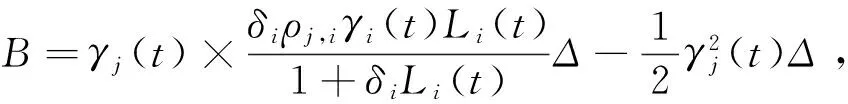
4.2 模型的MCMC参数估计过程
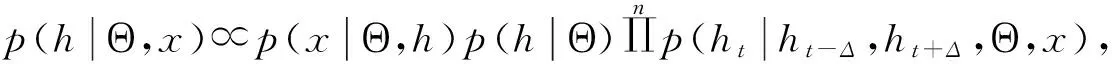
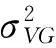
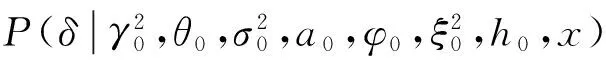
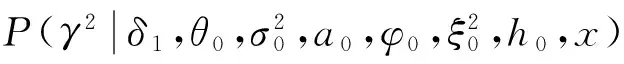
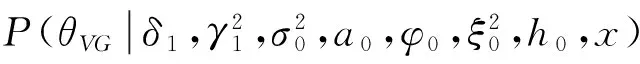
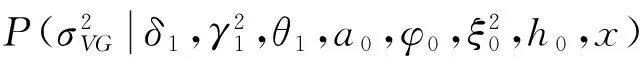
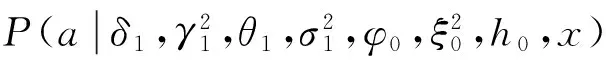
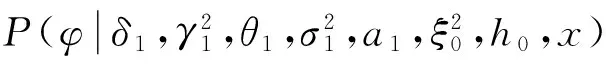
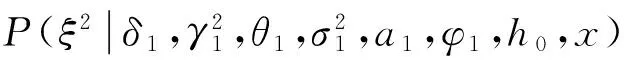
4.3 模拟计算
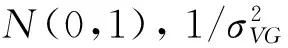

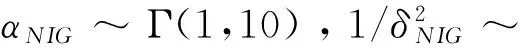
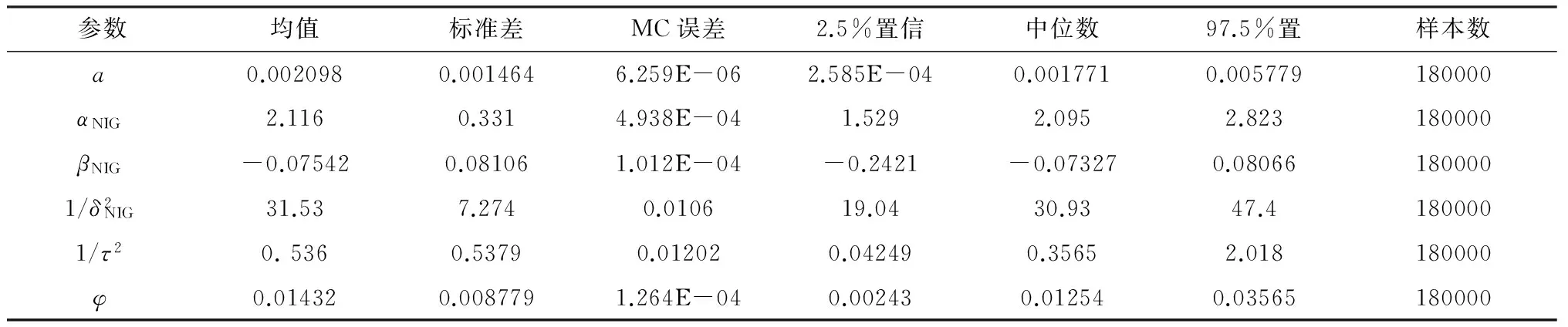
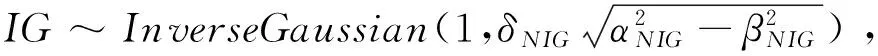
4.3 模型模拟与比较
5 结语
