高端装备制造业技术创新资源配置效率及影响因素研究
——基于两阶段StoNED和Tobit模型的实证分析
2018-03-09范德成杜明月
范德成,杜明月
(哈尔滨工程大学经济管理学院,黑龙江 哈尔滨 150001)
1 引言
近年来,中国工业一直保持着平稳快速的发展态势。然而,当前国际经济环境复杂多变,国内经济下行压力不断加大,面临困难与挑战,工业需要改革和调整,促进传统工业粗放的大规模生产和模仿创新逐步转向新兴工业集约的精益化生产和自主创新,以更好地适应增速放缓、结构优化、动力转换的经济发展新常态[1]。高端装备制造业作为一种技术密集的战略性新兴产业,在推动制造业转型升级过程中发挥着至关重要的引擎作用,同时也彰显着先进装备技术的核心竞争力。目前,相关部门注重培育和发展高端装备制造业,并且出台了一系列行业政策,在各地区加以部署、落实和推进。然而,这些政策在促进高端装备制造业发展的同时,也暴露出了缺乏核心技术、重复投资、资源分散、恶性竞争等棘手问题,亟待予以解决[2]。发展高端装备制造业关键在于技术创新,而人力、资金、物力等要素作为技术创新活动的基础资源,对其进行合理有效配置能够充分发挥创新投入的效用,提高创新成果转化和产出能力。由于效率是衡量产业技术创新能力的一项重要指标,再者高端装备制造业总体上仍处于起步阶段,在发展过程中容易受到内部因素和外部因素的影响,因此如何提升高端装备制造业技术创新资源配置效率,避免资源投入冗余和不足等问题的出现,准确把握影响效率的关键因素,突破当前部分体制机制壁垒和发展瓶颈,具有十分重要的理论意义和现实意义。
关于技术创新资源配置效率的内涵,目前学术界还没有权威清晰的界定,相关研究成果主要集中在技术创新效率和科技资源配置效率两个方面。Farrel[3]认为生产效率包括技术效率和配置效率;Afriat[4]最早提出技术创新效率的概念,认为投入产出比与生产可能性边界密切相关;Raab等[5]学者选取美国50个州的高技术产业作为研究样本,运用DEA模型测度技术创新效率;Nelson[6]和Porter[7]率先对科技资源配置情况进行研究,通过搜集相关历史数据对国与国之间的科技资源配置方式、科技经费支出以及科技创新政策进行比较分析;Schmidt等学者[8-9]对企业的研发人员与资金配置、研发方案选择等方面进行研究;官建成等[10]综合运用SBM-DEA和CEM-DEA模型对我国高技术产业技术创新效率进行深入分析;牛泽东[11]等运用SFA模型对我国装备制造业七大子行业技术创新效率进行测算,并对影响效率的关键因素进行具体分析;何海燕等[12]以企业为视角,运用统计方法着重分析技术壁垒对科技资源配置的影响;范斐等[13]运用比较优势模型作实证分析,认为我国科技资源配置存在显著的地区差异;汪朗峰等[14]运用SFA模型分析科技资源配置效率对高技术产业发展影响的总体和阶段特征;黄海霞等[15]运用DEA模型分析我国战略性新兴产业的科技资源配置效率水平。关于相关影响因素分析,已有研究主要考察企业规模、所有制结构、市场结构、融资结构等几个方面。比如,Scherer和Ross[16]认为规模较大的企业由于管理控制过度或者不到位会抑制技术创新效率的提高,Chen等[17]则认为规模经济效应有助于提升技术创新效率;Zhang,Anming[18]认为由于产权不明晰、管理制度僵化等问题的存在,国有成分与企业研发效率呈负相关关系,冯根福等[19]则认为国有比重高的行业与研发效率存在正相关关系;陈修德等[20]认为市场竞争程度对技术创新效率起反作用,与熊彼特关于垄断有利于技术创新的观点一致,朱有为等[21]则发现市场竞争在一定程度上对技术创新效率起正作用;白俊红等[22]认为政府支持对技术创新效率具有负影响。总结国内外文献发现:内容上,学者们分别在区域、产业以及企业层面对技术创新效率和科技资源配置效率进行了深入研究,但对技术创新资源配置效率的研究尚不多;关于影响因素,学者们都对产业组织方面的影响因素十分重视,但观点存在很大差异,甚至相反。方法上,学者们主要运用DEA和SFA模型,其中,DEA的优点在于无需指定生产函数形式或分布假设,避免设定误差,解决了决策单元的最优化问题,并且能够提供多个效率测算指标,缺点在于将任何对生产可能边界的偏离都度量为非效率成分,未能将随机误差分离出来;SFA的优点在于能够对纯粹的随机误差和非效率项进行有效分离,缺点在于不恰当的生产函数形式或误差项的分布假设可能会将设定误差和效率估计混淆在一起[23]。鉴于此,本文综合考虑技术创新效率和科技资源配置效率,基于行业面板数据,运用动态随机非参数数据包络模型和Tobit模型对高端装备制造业技术创新资源配置效率以及影响因素进行整体和阶段分析,进而弥补一定研究不足。
2 研究方法
2.1 随机非参数数据包络分析法
随机非参数数据包络分析法(StoNED)首先由学者Kwosmanen[24-25]提出,该方法是在传统DEA和SFA模型的基础上建立和发展起来的。其中,确定成分采用与DEA相同的非参数处理方式,所引入的随机成分通常遵循SFA的设定方法。因此,StoNED不仅有效地避免了因生产函数形式预设导致误差与效率估计相混淆的缺陷,而且能够较好地将随机误差项与非效率项进行合理分离,换言之,StoNED结合了DEA和SFA两者的优点。在之前的学术成果中,StoNED模型多数应用于截面数据,属于静态随机非参数数据包络模型[26-27]。为了更好地理解StoNED模型,本文在介绍静态随机非参数数据包络模型的基础上,采用一种应用于面板数据的StoNED模型,即动态随机非参数数据包络模型,其最大的特点在于模型中包含时间变量,使得效率能够在时间上进行比较。
2.1.1 静态随机非参数数据包络模型
该部分主要介绍一种基于多投入单产出的截面StoNED模型:投入向量用x表示,产出向量用y表示,经典生产函数y=f(x)表示生产技术,f表征着生产可能集边界,目的是用数据来估计先验、未知的生产函数。参照DEA模型,假设生产函数是单调递增的凹函数,没有特定的函数形式;参照SFA模型,将参数引入到模型之中,使之不同于DEA模型。由于残差εi=vi-ui,i=1,…,n的出现,可能会导致产出观测值yi不等于真实值f(xi)。组合残差项εi包括非效率项ui(ui>0)和误差项vi,生产函数的具体形式如下:
yi=f(xi)+εi=f(xi)-ui+vi
(1)
对比SFA模型所采用的改进最小二乘法(MOLS),StoNED模型采用一种被称为凹面非参数最小二乘法(CNLS)的回归技术。CNLS不同于OLS之处在于采用了更普通的非参数回归方程形式,而且此回归方程考虑了单调性和凹性。CNLS模型可以写成一个二次规划问题:
(2)
对比OLS估计,CNLS允许截距和斜率随着样本个体变化而改变,与SFA模型相似之处在于该模型也具有n个不同斜率向量βi。随机参数模型采用相同、特定的函数形式来估计n个不同生产函数,而CNLS模型采用一种非特定的生产函数形式来估计n个切超平面。第一个约束条件为线性回归方程,其中斜率βi代表投入要素i的边际产出;第二个约束条件采用不等式形式对生产函数施加凹性限制;第三个约束条件对生产函数施加了单调递增限制。
为了将非效率项ui和误差项vi分离,首先采用矩估计的方法计算二阶中心矩和三阶中心矩:
(3)
式(3)中的m2和m3分别为真实矩μ2和μ3的一致估计量,进一步得到:
(4)
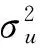
(5)
其中φ表示标准正态概率密度函数,Φ表示标准正态分布函数[23]。
由于观测值yi与真实值f(xi)的差异不是由误差项引起的,而是由非效率项导致的,故在公式(1)的等号两边同除以f(xi)得到公式:
(6)
由于E(vi)=0,故公式(6)可改写为:
(7)
2.1.2 动态随机非参数数据包络模型
起初在研究随机非参数数据包络模型时,曾假设生产技术和效率项不随时间变化而变化。现在允许生产函数能够呈现出技术进步或退步,把时间变量t纳入生产函数f当中,并把生产函数写作f(x,t),t=0,1,…,T。同理,将非效率项ui用函数ui(t)代替,i=1,…,n。另外,将组合残差项设定为乘法形式而不是加法形式,以此来降低异方差的影响,得到新的StoNED模型:
yit=f(xit,t)/(1+ui(t)-vit)
(8)
yit=f(xit,t)-ui(t)·yit+vit·yit
(9)
借助生产函数f(x,t)可以得到多种设置技术进步的方式,现假设技术进步是投入、产出量较高型的,不妨将函数f(x,t)写为:
(10)
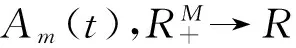
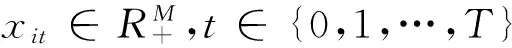
以上两条性质能显示出模型(10)的通用性,也说明在此模型框架内设置技术变化是十分方便的。于是可以采用非参数的形式来估计基期生产函数f(xit,0),采用非参数或参数的形式来设置技术变化函数Am(t)。更为重要的是,不管如何设置函数Am(t),基期生产函数f(xit,0)的凹性在各个时期均能保持一致。
纯非参数函数可写成以下特定的形式:
Am(t)=γmt
(11)
其中,γmt对投入和时间来说是一个常量,将大量新的未知参数引入到模型之中;相对而言,选取一种参数近似形式可以减少不必要未知参数的过多引入。比如,采用二次方程的形式:
Am(t)=θmt+ψmt2
(12)
若假设技术退步不出现,则应满足约束条件:
Am(t+1)≥Am(t),∀t=0,1,…,T-1
(13)
在凹面非参数最小二乘法(CNLS)的框架中,采用纯非参数的形式来设定效率变化是不可行的,除非添加一些严格的约束条件,若没有这些约束条件,则效率变化很难与随机误差区分开。因此,采用半参数方法,即以非参数的形式来估计生产函数,非效率函数ui(t)用参数方程来近似表达。参照Cornwelletal[28]的处理方式,将ui(t)设定为二次多项式的特定形式:
ui(t)=ai+bit+cit2
(14)
若bi=ci=0,则认为效率保持稳定不变;若bi>0且ci=0,则认为效率线性增长;若bi>0且ci≠0,则认为效率表现为非线性变化;另外,常数ai可解释为阶段初期的非效率水平。
将式(10)、(12)、(14)结合到StoNED模型(9)中,得到待估计回归方程:
-(ai+bit+cit2)yit+vityit
(15)
为了估计未知的基期生产函数f(xit,0)以及参数α,β,θ,ψ,a,b,c,v,构建凹面非参数最小二乘法(CNLS)估计模型:
(16)
其中,目标函数旨在计算随机误差项vit平方和的最小值;第一个约束条件代表回归方程,基期生产函数f(xit,0)用切超平面αit+βitxit来表示;第二个约束条件对切超平面施加了凹性限制;第三个约束条件对生产函数f(xit,t)施加了单调递增限制;第四个约束条件对技术变化进行了非负限制,即Am(t)≥0。根据基期生产函数的性质,结合模型(16)的约束条件,可以保证生产函数f(xit,0)的凹性和单调性[29]。
总之,效率的测度必须由模型(16)间接得出,效率值E可采用以下标准化形式表示:
(17)
2.2 Toibt模型
为了进一步了解高端装备制造业技术创新资源配置效率的显著性影响因素,本文以StoNED模型所测算的效率作为被解释变量,以各个影响因素作为解释变量,设定多元线性回归方程。由于效率取值大于0,数据被限制在特定的区间之内,属于截断问题,倘若直接采用普通最小二乘法,可能会导致结果偏移或不一致。因此,本文采用受限因变量模型中的规范截取回归模型,亦称为Toibt模型。具体形式如下:
(18)
其中:Yk为受限的被解释变量,Xk为解释变量,β为未知参数向量,μk~N(0,σ2)。
3 变量选取与数据处理
3.1 统计分类
高端装备制造业是指生产制造高技术、高附加值的先进工业设施设备的行业。目前,我国高端装备制造业缺乏明确的统计分类标准,相关调查体系尚未得到建立,致使在获取相关数据方面难以形成统一的规范。由于高端装备制造业归属于战略性新兴产业的范畴,因此本文参考国家统计局编制并发布的《战略性新兴产业》(试行)、《高技术产业统计分类目录》以及《国民经济行业分类标准》,结合相关文献对战略性新兴产业的分类研究[15],按照科学性、合理性、大口径、一致性以及可获得性的原则,将高端装备制造业(I0)划分为七大子行业,分别包括:通用设备制造业(I1)、专用设备制造业(I2)、电气器械及器材制造业(I3)、仪器仪表及文化办公机械制造业(I4)、交通运输设备制造业(I5)、航空航天设备制造业(I6)和医疗设备及仪器制造业(I7)。
3.2 数据来源
本研究所需要的原始数据主要来源于《中国统计年鉴》、《中国工业经济统计年鉴》、《中国科技统计年鉴》、《工业企业科技活动统计年鉴》和《中国高技术产业统计年鉴》。然而,在获取数据时出现统计口径不一致的问题:比如,1998年至2006年的统计范围是全部国有企业和年主营业务收入在500万元以上的非国有工业企业;2007年至2010年的统计范围是年主营业务收入在500万元及以上的工业企业;2011年及以后年份的统计范围是年主营业务收入在2000万元以上的工业企业。统计口径随时间发生了分段变化,为保证样本数据具有可比性,本文采用2011-2014年的数据,通过选取有统一口径的区间来规避此类问题。
3.3 变量选取及处理
产业技术创新活动是一项复杂的系统工程,相关研究主要包含两种角度:一种是将其作为整体进行分析[10,21],另一种则根据价值链理论将其划分为技术研发和技术转化两个阶段进行分析[30-31],技术创新活动伴随着资源的持续配置,而且容易受到内外部因素影响。产业技术创新资源配置效率指的是在产业内部协调、整合和分配资源,使配置后的创新要素按照一定比例实现最优组合,进而发挥出最大效能[32]。为了能够正确利用StoNED和Tobit模型测度高端装备制造业技术创新资源配置效率并分析其影响因素,关键是要合理地选择投入、产出变量以及影响因素变量。由于技术研发和技术转化阶段效率关联密切,且均可能影响整体效率,因此本文采用两阶段的研究方式,相关变量的选取和处理如下:
3.3.1 技术研发阶段的投入产出变量
该阶段的资源投入通常从人力和资金两个方面考虑,研发人员和研发经费被认作技术创新活动中的重要组成部分。比如,有的学者采用R&D人员数量和R&D经费支出作为技术研发阶段的投入变量[33]。充分考虑研发的基本投入要素,本文选取R&D人员全时当量(F1)、R&D经费内部支出(F2)以及新产品开发经费支出(F3)作为技术研发阶段的投入变量;专利数作为国际上通用的创新产出指标,主要分为专利申请数、有效发明专利数和专利授权数[34],由于专利申请量高于有效发明专利量,能够更全面地反映科技产出,而专利授权量受主观因素的影响,因此本文选择专利申请量(F4)作为技术研发阶段的产出变量,其中,R&D经费内部支出和新产品开发经费支出均采用存量的形式。具体的计算过程为:首先运用加权R&D价格指数对R&D经费内部支出进行平减[35],消除价格变化的影响,以2011年为不变价格;然后借鉴Griliches和Goto等学者[36-37]的处理方法,采用永续盘存法(PIM)对价格平减后的R&D经费内部支出进行存量估算,基期为2011年,计算公式如下:
RDEi,t=(1-δ)RDEi,t-1+Ei,t
(19)
其中:RDEi,t与RDEi,t-1分别表示第i个产业在第t年和第t-1年的R&D经费内部支出存量;Ei,t表示第i个产业在第t年的R&D经费内部支出;δ为折旧率,本文取δ=15%。基期R&D经费内部支出存量的计算公式如下:
(20)
其中:Ei,1表示基期价格不变的R&D经费内部支出;δ为折旧率;g为所研究时段内R&D经费内部支出的年增长率。新产品开发经费支出存量的估算方法与R&D经费内部支出相同。
3.3.2 技术转化阶段的投入产出变量
该阶段的资源投入通常从人力、资金和技术三个方面考虑,至于人力方面,本文选取年末从业人员数(F5)作为人力投入变量;至于资金方面,有的学者采用技术改造经费支出存量作为资金投入变量[38],由于目前我国自主创新能力较为薄弱,仍然以模仿创新和渐进性创新为主,故本文采用非研发经费支出(F6)作为资金投入变量,以非研发经费支出除以10%作为基期资本存量[39],基期为2011年,其它处理方法与R&D经费内部支出相同,非研发经费支出包括技术引进费用支出、技术消化吸收费用支出、技术改造费用支出以及购买国内技术费用支出;至于技术方面,专利申请数(F4)作为中间变量,既可以作为上一阶段的产出变量,又可以作为本阶段的投入变量,因此本文采用专利申请数作为技术转化阶段的技术投入变量。另外,产出变量通常包括新产品销售收入、新产品产值和新产品开发项目数,由于新产品产值部分数据缺失,而新产品开发项目数又带有一定主观色彩,因此本文采用新产品销售收入(F7)作为技术转化阶段的创新产出变量,并利用工业生产者出厂价格指数对其进行平减,以2011年为不变价格。
3.3.3 影响因素变量
本文着重从产业组织的视角分析高端装备制造业技术创新资源配置效率(EFF)的影响因素,分别从产业组织的三个要素中选取影响因素变量。厂商要素:企业规模(ES)一般采用企业数量或年末从业人员数表示,本文选取企业平均产值,即行业工业总产值与企业数量的比值来反映企业规模;所有制结构(OS)采用分行业国有企业工业总产值占所统计的全部工业企业总产值的比重表示,其中,相关工业总产值选用工业GDP指数进行平减,以2011年为不变价格。市场要素:市场集中度(MC)能够有效地反映垄断或竞争程度,本文选用各个子行业的企业数占整个行业企业总数的比重对市场集中度进行度量,其中,市场集中度为反向指标,即数值越大,市场集中度越小,反之亦然[40]。产业政策要素:政府支持(GS)贯穿于整个科技创新活动之中,本文选取政府资金占研发经费内部支出的比重来表征政府支持[41]。
4 实证分析
4.1 高端装备制造业技术创新资源配置效率的测度结果分析
经典的数据包络模型将决策单元视为“黑箱”,忽视中间环节,评价结果与客观实际相比有所偏差,难以探析上游和下游阶段的运作效率对整体效率的影响,而关联型两阶段解析模型可以有效弥补以上不足[42]。鉴于此,本文选择高端装备制造业全行业以及下属的七大子行业作为研究对象,采用动态随机非参数数据包络模型,分别测度技术研发、技术转化两阶段以及整体技术创新资源配置效率。结合模型(16),设定为以下形式:
(21)
其中:L、K和M分别表示人力、资金和技术或其它投入要素。模型(21)可以运用GAMS软件进行求解和相关参数估计,最终得到高端装备制造业技术创新资源配置的整体效率(EFF)和技术研发、技术转化两阶段效率值(EFF(1)和EFF(2)),具体数据见表1。

表1 高端装备制造业技术创新资源配置效率值
注:CV(CoefficientofVariation)表示变异系数,是针对七大子行业而言的,数据均保留五位小数,下同。
表1给出的是高端装备制造业全行业和子行业在2011-2014年的技术创新资源配置效率值,均值以及变异系数。其中,效率均值反映的是技术创新资源配置的总体情况。从全行业角度来看,整体效率为0.60491,技术研发阶段效率为0.56268,技术转化阶段效率为0.81490,以0.5为基准,高端装备制造业技术创新资源配置效率在整体和技术研发阶段均处于中游偏上水平,技术转化阶段效率处于较高水平,技术转化阶段效率比技术研发阶段高,属于低研发高转化资源配置效率型。从子行业角度来看,整体和分阶段效率均表现出行业异质性,差异比较明显。交通运输设备制造业整体和技术转化阶段效率最高,分别为0.83715和0.97706,然而技术研发阶段效率为0.40961,处于中等偏下水平,技术转化阶段效率比技术研发阶段高,说明该行业属于低研发高转化资源配置效率型;医疗设备及仪器制造业技术研发阶段效率为0.77444,效率最高,而整体和技术转化阶段效率相对较低,分别为0.40617和0.55095,技术研发阶段效率比技术转化阶段高,说明该行业属于高研发低转化资源配置效率型;航空航天设备制造业整体、技术研发以及技术转化阶段效率最低,分别为0.17541、0.20217和0.49280,技术转化阶段效率比技术研发阶段高,说明该行业属于低研发高转化资源配置效率型。
由于高端装备制造业属于新兴产业,尚处于初始发展阶段,内外部环境不稳定,各行业在人力、经费、创新平台等方面可能存在一定差异,发展水平可能会随着时间的推移不断发生变化,下面着重分析高端装备制造业技术创新资源配置效率的变化特征和趋势。
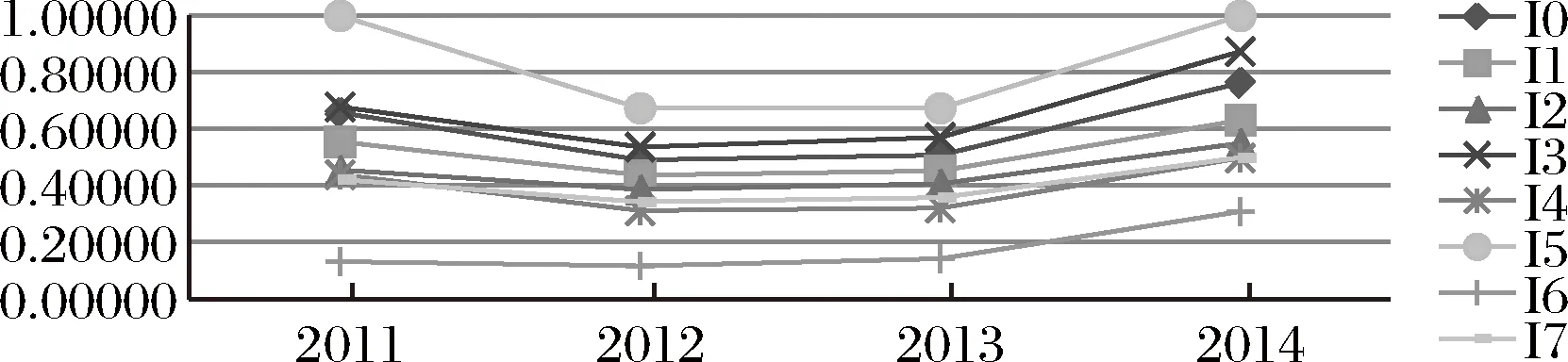
图1 高端装备制造业技术创新资源配置整体效率变化
图1描绘的是高端装备制造业全行业以及子行业技术创新资源配置整体效率随时间推移的变化特征,直观来看,图中8条曲线在2011-2014年间的走势大体一致,且基本呈U型变化。具体来说,所有行业的整体效率均在2011-2012年下降,在2012-2014年回升,其中交通运输设备制造业在2012和2013年保持效率不变,均为0.67431,在2011和2014年效率最高,为1.00000,而且其效率值在2011-2014年均高于其它产业,说明交通运输设备制造业技术积累较为深厚,在行业应用方面较为成熟,资源配置优于其它产业;航空航天设备制造业的整体效率值在2011-2014年均低于其它产业,由于行业自身的特殊性,相关技术一直处于前沿位置,虽然技术革新空间较大,但攻坚难度也会随着不断探索而增大,创新资源配置效率低于其它产业。
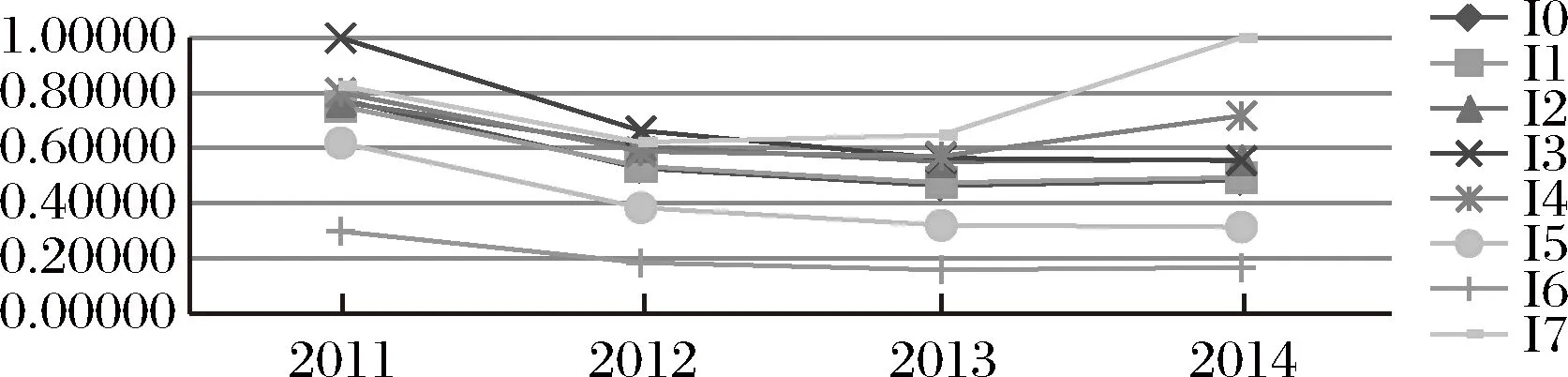
图2 技术研发阶段的高端装备制造业技术创新资源配置效率变化
图2描绘的是高端装备制造业全行业以及子行业技术创新资源配置效率在技术研发阶段随时间推移的变化特征,直观来看,图中8条曲线在2011-2014年出现了三种走势。具体来说,通用设备制造业、专用设备制造业、仪器仪表及文化办工机械制造业、航空航天设备制造业以及整个高端装备制造业的效率值均在2011-2013年呈现下降态势,在2013-2014年又有所回升,医疗设备及仪器制造业的效率值在2011-2012年呈现下降态势,在2012-2014年保持上升态势,呈U型波动,说明研发前期投入大量人力、资金等资源,经过一段时间消化,冗余现象逐渐得到缓解,产出不断增多,效率有所提高;电气器械及器材制造业和交通运输设备制造业的效率值在2011-2014年一直处在下降过程中,说明两者研发起动优势较为凸出,但后劲略显不足。
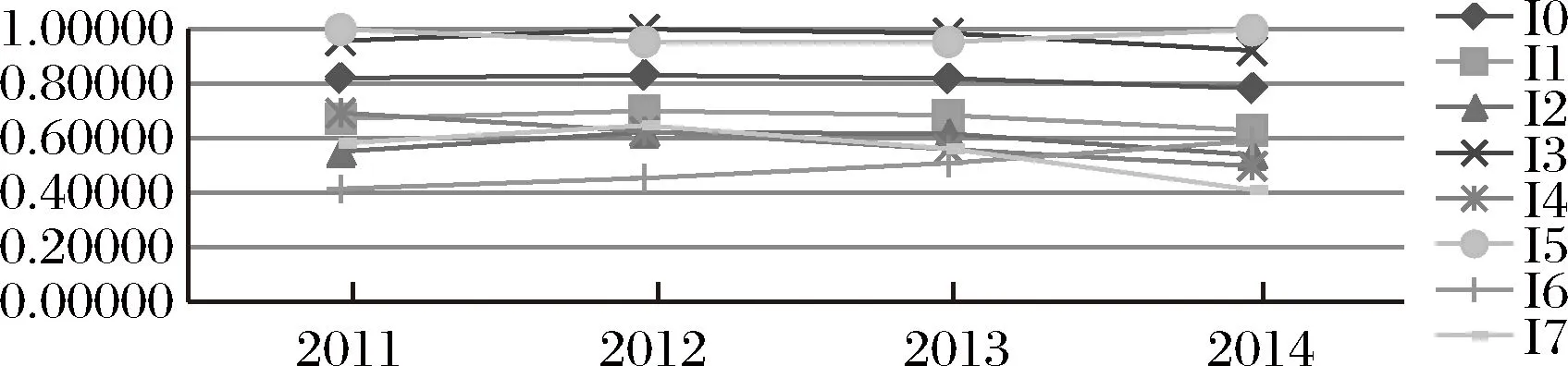
图3 技术转化阶段的高端装备制造业技术创新资源配置效率变化
图3描绘的是高端装备制造业全行业以及子行业技术创新资源配置效率在技术转化阶段随时间推移的变化特征,直观来看,图中8条曲线在2011-2014年出现了四种走势。具体而言,通用设备制造业、专用设备制造业、电气器械及器材制造业、医疗设备及仪器制造业以及整个高端装备制造业的效率值在2011-2012年呈现上升态势,在2012-2014年呈现下降态势,其中,电气器械及器材制造业在2012年效率最高,为1.00000,这些行业市场进入壁垒较小,短期优势明显,商品能够迅速投入市场并转化为收入,但随着市场逐渐饱和,需求动力又表现不足;仪器仪表及文化办工机械制造业的效率值在2011-2014年保持稳定的下降趋势,原因可能是产业化层次低,发展模式比较粗放,劳动人员结构冗杂;交通运输设备制造业在2011年效率最高,为1.00000,在2012和2013年保持效率不变,降为0.95511,而且效率值在2013-2014年又出现了一定程度的回升,该行业市场结构属于垄断竞争类型,产品差异不大,技术转化效率有高有低;航空航天设备制造业的效率值在2011-2014年一直保持稳定的上升态势,研发阶段需要技术攻关,成果积累缓慢,但在此阶段开始逐步得到转化。
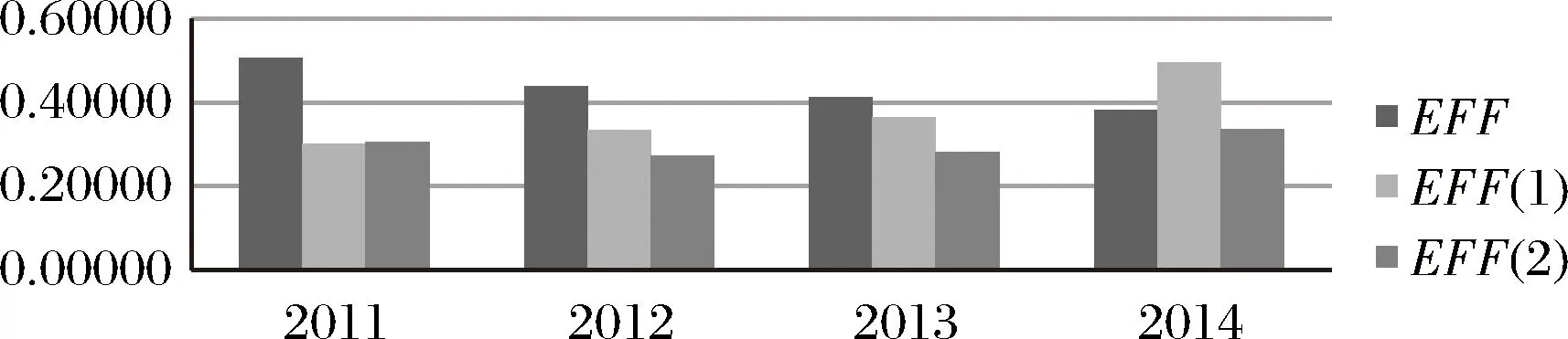
图4 高端装备制造业技术创新资源配置效率的变异系数
图4描绘的是高端装备制造业技术创新资源配置效率分别在整体、技术研发以及技术转化阶段的变化趋势,直观来看,整体效率的变异系数逐渐减小,技术研发阶段效率的变异系数逐渐增大,技术转化阶段效率的变异系数呈现U型变化态势,且在2012年出现分水岭。变异系数采用样本数据的标准差与数学期望的比值来表示,在进行数组之间离散程度比较时,是一个比较理想的衡量尺度。具体而言,整体效率的变异系数在2011-2014年之间从0.50630递减至0.38156,表明效率变化逐步趋于收敛,高端装备制造业各个子行业技术创新资源配置效率的差距随着时间的推移在不断缩小;技术研发阶段效率的变异系数在2011-2014年之间从0.30235递增至0.49525,表明效率变化逐步趋于发散,高端装备制造业各个子行业技术创新资源配置效率的差距随着时间的推移在不断拉大;技术转化阶段效率的变异系数从2011年开始至2012年,由0.30681减至最小,数值为0.27241,从2012年至2014年,逐步增加到0.33551,表明效率变化趋势不稳定,开始趋于收敛,然后又趋于发散,高端装备制造业各个子行业技术创新资源配置效率的差距随着时间的推移先变小后变大。
4.2 高端装备制造业技术创新资源配置效率的影响因素分析
为了从产业组织的视角分析高端装备制造业技术创新资源配置效率的关键影响因素,本文采用基于面板数据的Tobit模型,分别建立高端装备制造业在整体、技术研发以及技术转化阶段上的多元线性回归方程,具体形式为:
EFFi,t=C+α1ln(ESi,t)+α2ln(OSi,t)+α3ln(MCi,t)+α4ln(GSi,t)+εi,t
(22)
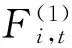
(23)
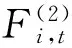
(24)
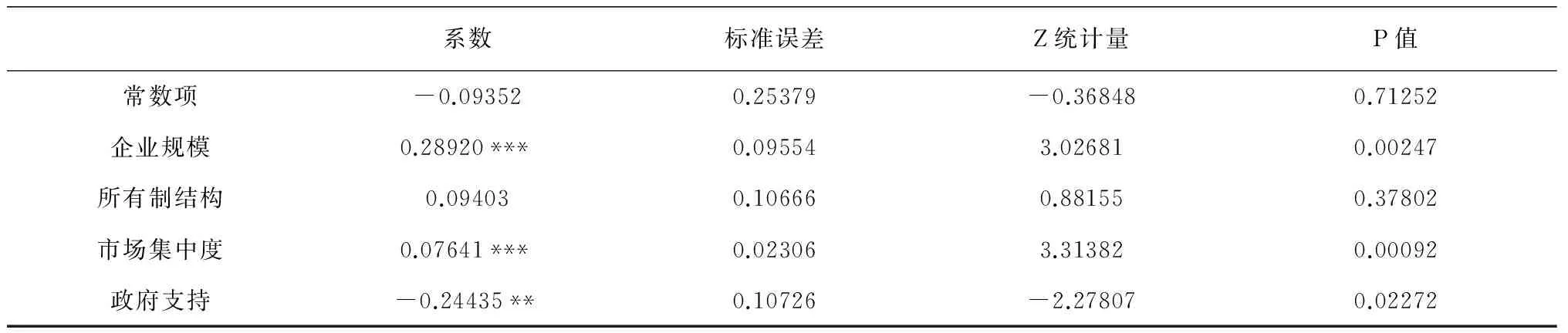
表2 高端装备制造业技术创新资源配置整体效率影响因素的Toibt回归结果
注:*表示10%的显著性水平,**表示5%的显著性水平,***表示1%的显著性水平,下同。
在整体效率方面,由表2中的回归结果可以得到:除了所有制结构以外,企业规模、市场集中度以及政府支持这三个自变量都通过了显著性检验。具体而言,所有制结构的回归系数为0.09403,没有通过显著性检验,表明所有制结构并没有对高端装备制造业技术创新资源配置整体效率起作用;企业规模的回归系数为0.28920,通过了1%的显著性水平检验,表明企业规模与高端装备制造业技术创新资源配置整体效率正相关,前者对后者起到一定促进作用,即企业规模越大,效率越高,原因可能是从研发投入开始到最终产出,厂商的规模经济效应经历较长时期之后终于得以实现,或者说企业规模不断扩大有助于整体效率的提升;市场集中度的回归系数为0.07641,通过了1%的显著性水平检验,表明市场集中度与高端装备制造业技术创新资源配置整体效率正相关,而市场集中度为反向指标,因此市场集中度数值越小,垄断程度越高,效率越低,原因可能是垄断市场不利于技术创新资源配置整体效率的提升,垄断型产业往往满足技术创新带来的当前利润,导致产业缺乏技术创新动力,因此适度的市场竞争有利于技术创新资源配置整体效率的提升,而且能够在较长时期内推动技术实现革新和突破;政府支持的回归系数为-0.24435,通过了5%的显著性水平检验,表明政府支持与高端装备制造业技术创新资源配置整体效率负相关,前者对后者起到一定抑制作用,即政府支持越多,效率越低,原因可能是政府以资金支持的形式直接介入到科技创新活动之中,容易造成挤出效应,企业在资金周转方面相对粗放,缺乏精细管理和责任意识,导致技术创新资源配置整体效率偏低。
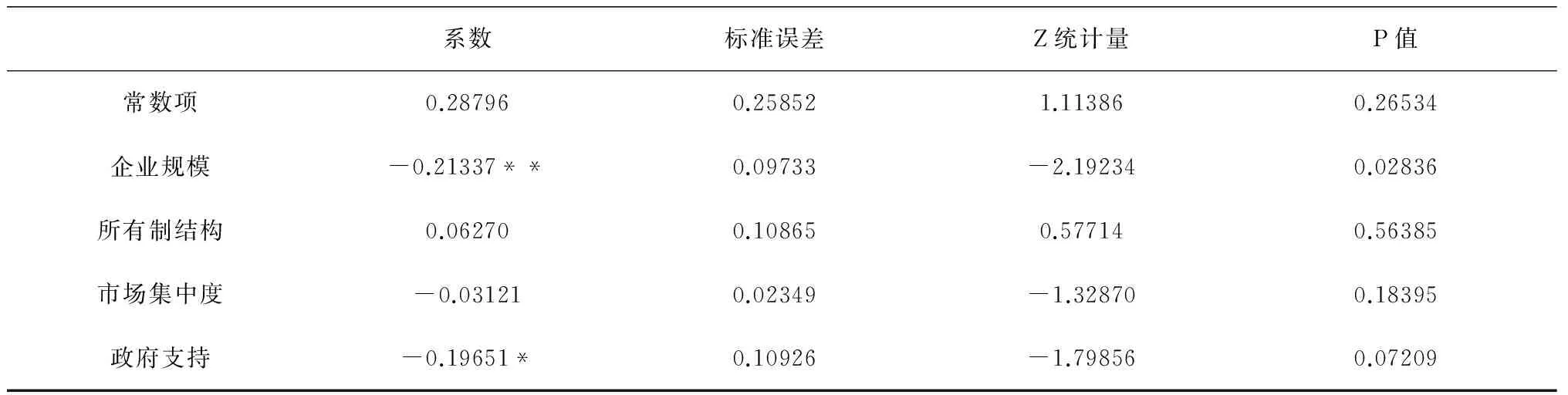
表3 技术研发阶段高端装备制造业技术创新资源配置效率影响因素的Toibt回归结果
在技术研发阶段,由表3中的回归结果可以得到:解释变量中只有企业规模和政府支持这两个变量通过了显著性检验,所有制结构和市场集中度均未通过显著性检验。具体而言,企业规模的回归系数为-0.21337,通过了5%的显著性水平检验,表明企业规模与技术研发阶段的高端装备制造业技术创新资源配置效率负相关,前者对后者起到一定抑制作用,即企业规模越大,效率反而越低,原因可能是由于时滞性的存在,技术研发阶段的高投入在短期内未能得到相应的产出,导致技术创新资源配置效率低下;所有制结构的回归系数为0.06270,没有通过显著性检验,表明所有制结构并没有对技术研发阶段的高端装备制造业技术创新资源配置效率起作用;市场集中度的回归系数为-0.03121,也没有通过显著性检验,表明市场集中度并没有对技术研发阶段的高端装备制造业技术创新资源配置效率起作用,原因可能是虽然市场垄断在人力、资金等方面存在固有优势,但是在技术研发过程中,这种优势在短期之内难以得到实现,导致其对技术研发阶段效率作用不明显;政府支持的回归系数为-0.19651,通过了10%的显著性水平检验,表明政府支持与技术研发阶段的高端装备制造业技术创新资源配置效率负相关,前者对后者起到一定抑制作用,即政府支持越多,效率越低,原因与整体效率分析相同。

表4 技术转化阶段高端装备制造业技术创新资源配置效率影响因素的Toibt回归结果
在技术转化阶段,由表4中的回归结果可以得到:解释变量中只有所有制结构未通过显著性检验,其余变量均通过显著性检验。具体而言,企业规模的回归系数为0.42305,通过了1%的显著性水平检验,表明企业规模与技术转化阶段的高端装备制造业技术创新资源配置效率正相关,前者对后者起到一定促进作用,即企业规模越大,效率越高,原因可能是企业规模与技术创新资源配置效率存在某种U型关系,效率随着企业规模的扩大出现短暂的下降之后,技术手段逐渐趋于成熟,初期和中间投入开始得到相应的转化和产出;所有制结构的回归系数为-0.02042,没有通过显著性检验,表明所有制结构并没有对技术转化阶段的高端装备制造业技术创新资源配置效率起作用;市场集中度的回归系数为0.07612,通过了1%的显著性水平检验,表明市场集中度与高端装备制造业技术创新资源配置整体效率正相关,而市场集中度为反向指标,因此市场集中度数值越小,垄断程度越高,效率越低,原因与整体效率分析相同;政府支持的回归系数为-0.17554,通过了5%的显著性水平检验,表明政府支持与技术转化阶段的高端装备制造业技术创新资源配置效率负相关,前者对后者起到一定抑制作用,即政府支持越多,效率越低,原因与整体效率分析相同。
5 结语
本文采用动态随机非参数数据包络模型,分整体和两阶段对2011-2014年我国高端装备制造业技术创新资源配置效率进行测度,并利用Tobit模型对效率的关键影响因素进行实证分析。研究的结论和政策启示主要有:
(1)高端装备制造业全行业的技术创新资源配置整体效率处于中等偏上水平,仍有较大上升空间,存在资源投入冗余或浪费、高投入低转化或低产出等问题;技术研发阶段效率处于中等水平,技术转化阶段效率处于较高水平,由于技术转化阶段是技术研发的下游阶段,因此技术研发阶段效率偏低成为整体效率未实现最优的制约因素,需要予以重点改进;高端装备制造业子行业之间存在不同程度的行业异质性,全行业以及各个子行业的技术创新资源配置效率变化特征有所异同,而且整体效率变化趋于收敛,技术研发阶段效率变化趋于发散,技术转化阶段效率变化呈现U型态势,即先收敛后发散。以上分析表明,目前我国高端装备制造业的发展尚处在初级阶段,技术创新资源配置还存在一定缺陷,产出投入比未能够实现最大化,仍然需要进行改善。
(2)企业规模对技术研发阶段效率具有负向作用,企业规模的扩大不利于中间产出效率提高;对技术转化阶段效率具有正向作用,企业规模的扩大有利于最终产出效率提高;对整体效率具有正向作用,企业规模的扩大导致最终产出与初始投入的比值增大,即效率得到提高,同时也反映了规模经济的阶段性变化。因此,相关部门应当优化企业规模结构,鼓励高端装备制造企业通过兼并、联合和股权转让等重组方式对技术创新资源进行有效配置,避免出现规模不经济和资源投入冗余或者浪费。
(3)市场集中度与整体和技术转化阶段效率正相关,而市场集中度为反向指标表明垄断不利于技术创新资源配置效率的提高;市场集中度对技术研发阶段效率作用不明显,说明垄断的优势因时滞性的存在未能得以体现。因此,产业内部与外部各方应努力营造适度、良性和充满活力的竞争环境,促使技术创新要素在市场范围内得到充分流动。
(4)政府支持对技术创新资源配置效率具有负向作用,表明过多的政府资金投入不利于效率的提高。因此,政府在制定相关优惠政策的同时,应当把产业中的企业视为技术创新主体,充分发挥市场的作用,而政府支持要确保科技活动经费投向基础性和公共性的技术创新领域。
[1] 黄群慧,李晓华.中国工业发展“十二五”评估及“十三五”战略[J].中国工业经济,2015,(9):5-20.
[2] 吕岩威,孙慧.中国战略性新兴产业技术效率及其影响因素研究——基于18个大类行业面板数据的分析[J].科学学与科学技术管理,2013,(11):137-146.
[3] Farrell M J.The measurement of productive efficiency[J].Journal of Royal Statistical Society,1957,20(3):253-281.
[4] Afriat S N.Efficiency estimation of production functions[J].International Economic Review,1972,13(3):568-598.
[5] Rabb R A,Kotamraju P.The efficiency of the high-tech economy:Conventional development indexes versus a performance index [J].Journal of Regional Science,2006,46(3):545-562.
[6] Nelson R.National systems of innovation:A Comparative Analysis [M].Oxford:Oxford University Press,1993.
[7] Porter M.Cluster and the new economic of competition[J].Harvard Business Review,1998,76(6):77-90.
[8] Schmidt R L.Stochastic optimization model to improve production planning and R&D resource allocation in biopharmaceutical production processes[J].Management Science, 1996,42(4):603-617.
[9] Liu C C,Chen C Y.A two-dimensional model for allocating resources to R&D programs[J].Journal of American Academy of Business,2004,5(1):459-473.
[10] 官建成,陈凯华.我国高技术产业技术创新效率的测度[J].数量经济技术经济研究,2009,(10):19-33.
[11] 牛泽东,张倩肖.中国装备制造业的技术创新效率[J].数量经济技术经济研究,2012,(11):51-67.
[12] 何海燕,林波,张剑.技术壁垒对我国企业科技资源配置的影响[J].科学学研究,2011,(6):856-860+839.
[13] 范斐,杜德斌,李恒.区域科技资源配置效率及比较优势分析[J].科学学研究,2012,(8):1198-1205.
[14] 汪朗峰,伏玉林.高技术产业发展中科技资源配置研究[J].科研管理,2013,(2):152-160.
[15] 黄海霞,张治河.基于DEA模型的我国战略性新兴产业科技资源配置效率研究[J].中国软科学,2015,(1):150-159.
[16] Scherer F M,Ross D.Industrial market structure and economic performance[M].Boston:Houghton Mifflin,1990.
[17] Chen C T,Chien C F,Lin M H,et al.Using DEA to evaluate R&D performance of the computers and peripherals firms in Taiwan[J].International Journal of Business, 2004,9(4):347-359.
[18] Zhang Anming, Zhang Yimin,Zhao R.A study of the R&D efficiency and production of Chinese firms[J].Journal of Comparative Economic,2003,31(3):443-464.
[19] 冯根福,刘军虎,徐志霖.中国工业部门研发效率及其影响因素实证分析[J].中国工业经济,2006,(11):46-51.
[20] 陈修德,梁彤缨.中国高新技术产业研发效率及其影响因素——基于面板数据SFPF模型的实证研究[J].科学学研究,2010,(8):1198-1205.
[21] 朱有为,徐康宁.中国高技术产业研发效率的实证研究[J].中国工业经济,2006,(11):38-45.
[22] 白俊红,江可申,李婧.应用随机前沿模型评测中国区域研发创新效率[J].管理世界,2009,(10):51-61.
[23] 籍艳丽,赵丽琴.一种效率测度的新方法:随机非参数数据包络分析法[J].统计与决策,2011,(5):33-34.
[24] Kuosmanen T.Stochastic nonparametric envelopment of data: Combining virtue of SFA and DEA in a unified framework[R].Discussion Paper,MTT Agrifood Research Finland,2006.
[25] Kuosmanen T.Stochastic nonparametric envelopment of panel data:Frontier estimation with fixed and random effects approaches[R].Discussion Paper,MTT Agriffood Research Finland,2007.
[26] 周四军,王欣,胡瑞.中国商业银行X效率测度——StoNED方法与超效率DEA方法的比较研究[J].统计与信息论坛,2012,(4):3-9.
[27] 袁丽静,杨琼.基于StoNED模型的技术效率半参数分析——以钢铁行业为例[J].财经问题研究,2015,(5):35-41.
[28] Cornwell C,Schmidt P,and Sickles R.Production frontiers with cross sectional and time series variation in efficiency levels[J].Journal of Econnometrics 1990,46(1-2):185-200.
[29] 汪茂泰,何永芳.动态随机非参数数据包络分析法及其应用[J].统计与决策,2015,(21):83-85.
[30] 郑坚.高技术产业技术创新效率评价的改进DEA方法研究[D].哈尔滨;哈尔滨工业大学,2008.
[31] 肖仁桥,钱丽,陈忠卫.中国高技术产业创新效率及其影响因素研究[J].管理科学,2012,25(5):85-98.
[32] 王亮.区域创新系统资源配置效率的演进规律与创新机制研究[D].长春:吉林大学,2008.
[33] Sharma S,Thomas V J.Inter-country R&D efficiency analysis:An application of data envelopment analysis[J].Scientometrics,2008,76(3):483-501.
[34] Guan Jiancheng,Gao Xia.Exploring the H-index at patent level[J].Journal of the American Society for Information Science and Technology,2009, 60(1):35-40.
[35] 刘伟,陈菁泉,李星星.中国省际高新技术产业技术创新的TFP测算及收敛趋势研究[J].经济理论与经济管理,2013,33(1):36-50.
[36] Griliches,Z.R&D and the productivity slowdown [J].American Economic Review,1980,70(2):343-348.
[37] Goto A,Suzuki K.R&D capital,rate of return on R&D investment and spillover of R&D in Japanese manufacturing industries [J].The Review of Economics and Statistics,1989,71(4):555-564.
[38] 刘伟.基于Bootstrap-Malmquist指数的高新技术产业技术创新效率分析[J].经济学动态,2013,(3):42-52.
[39] 张军,吴桂英,张吉鹏.中国省际物质资本存量估算:1952-2000[J].经济研究,2004,(10):35-44.
[40] 张娜,杨秀云,李小光.我国高技术产业技术创新影响因素分析[J].经济问题探索,2015,(1):30-35.
[41] 肖文,林高榜.政府支持、研发管理与技术创新效率——基于中国工业行业的实证分析[J].管理世界,2014,(4):71-80.
[42] 王美强,李勇军.具有双重角色和非期望要素的供应商评价两阶段DEA模型[J].中国管理科学,2016,24(12):91-97.
