巧设数学问题 引领探究活动
2018-03-08徐婧刘铭刘圣良
徐婧 刘铭 刘圣良


教学内容:人教版五年级上册第六单元第一课时86~88页。
教学目标:
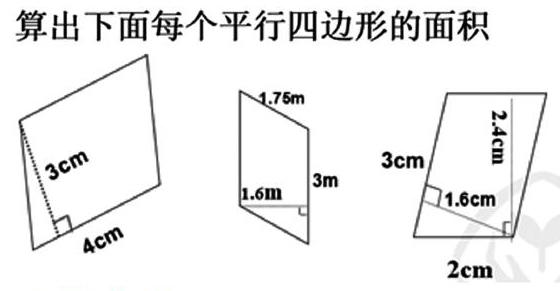
1.理解并掌握平行四边形的面积计算公式,会计算平行四边形的面积。
2.通过操作、观察、比较等活动,初步认识转化的方法,培养学生的观察、分析、概括、推理能力、发展学生的空间观念。
3.感受数学与生活的紧密联系,体验学习数学的乐趣。
教学重点:探索并掌握平行四边形的面积计算公式,并能正确地计算平行四边形的面积。
教学难点:探究平行四边形面积计算公式的推导过程。
教具学具:课件、若干个平行四边形、剪刀。
教学流程:
一、 创设情境,生成问题
师:同学们,这是一幅校园门前的街道平面图,观察这幅平面图,你发现了哪些我们学过的平面图形?
生1:斑马线是长方形。
生2:屋顶是梯形。
生3:指示牌是三角形。
生4:校门前的两个花坛一个是长方形,另一个是平行四边形。
师:你们真是火眼金睛,找到这么多的平面图形。要想知道这两个花坛谁大,就要比较它们的面积,我们可以用什么方法比较出这两个图形的面积呢?
生1:我可以把图形放到格子纸上,数一数每个图形都占了几个格子,格子多的面积就大。
师:你这个方法真不错,利用了我们以前学习的工具——方格纸,解决了难题。
生2:我想把两个图形放在一起,多出来的那个面积就大。
师:把两个图形重叠在一起比较,这种方法也不错,一会儿我们动手试一试。
生3:老師,我想量一量正这个图形的边长,再想办法算一算面积。
师:这是我们解决这类问题的一般思路,可是量出了边长就可以算出面积吗?怎么算呢?这节课我们可以研究一下。
师:你们的方法可真多,那我们就按照同学们的想法看看能不能比较出这两个图形的面积。
二、 探索交流,解决问题
(一)数格子,提出猜想
1.出示活动一的要求。
(1)可以数方格(一个方格代表1m2,不满一格的都按半格计算),也可以画一画、拼一拼,数出图形的面积。
(2)填写表格。
学生自主学习,完成学习单一。
2.交流反馈,提出“转化”。
方法一:直接数
师:你是怎么数的?为什么这样数?(生汇报,师填写表格。)
生:我是一个一个数的,长方形的长是6个格子,宽是4个格子,所以面积就是24个格子。平行四边形的底是6,高是4,面积我是把不满一个的都按一格去计算,然后一个一个地数,就是24个格子。
师:这位同学是把不满一格的都按一格去计算,得出了图形的面积。还可以怎样做,能够运用更精确的方法得出图形的面积呢?
方法二:割补数
生1:将平行四边形沿着高剪下左侧的三角形再移到右边拼到缺少的那部分,就将平行四边形转化成了长方形。
师:老师特别赞同你的用词——转化。掌声送给这位同学。你非常有数学思想。
生2:从中间分割成两个梯形,旋转之后也将平行四边形转化成了长方形从而得到平行四边形的面积。
生3:将不满一格的拼在一起凑成一个整格,虽然没有变成长方形,但是也变成了规则图形,也可以精确地得到图形的面积。
师:我们通过这几种方法都得出了这两个图形的面积,回想刚才拼数的过程,观察图表,你发现了什么?
生1:我发现平行四边形和长方形的面积相等。
生2:我通过表格发现平行四边形的底和长方形的长相等,平行四边形的高和长方形的宽相等,面积当然也相等。
师:刚才我们是在格子纸上比较出了两个图形的面积,如果没有格子纸我们怎么办呢?,能不能将平行四边形转化成我们学过的图形再来推导出面积公式呢?
(二)动手实验,验证猜想
1.出示活动二要求:每位同学手中有两个完全相同的平行四边形纸片,可以选择其中的一个进行操作。
(1)画一画,剪一剪:你是沿着哪条线剪切的,先画下来。
(2)移一移,拼一拼:看看能不能将平行四边形转化成我们学过的图形。
(3)想一想:观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
(4)说一说:平行四边形的( )与长方形的( )相等
2.交流反馈,突出方法。
师:这里提出了几个要求?
生:我们可以先把高或者要剪的那条线画下来,再动手剪,最后将剪下来的部分移动拼补。(找几位学生上黑板演示自己的剪法,师巡视期间激发生思考不同方法。)
师:看明白了吗?有问题吗?都没有啊,我有:你是沿着哪儿剪的?我看下面有个同学随便拿起来就剪。
生1:沿着高剪、拼。
生2:从中间剪开(高)。(师追问:这也是高吗?引发学生思维的碰撞。)因为平行四边形有无数条高,从而得出结论:只要沿着高剪切,就可以将平行四边形转化成长方形。
生3:我受刚才割补法的启发,找出斜着两条边的中点,把它剪开,再拼补上,也可以把平行四边形转化成长方形。
生4:老师,我把这个平行四边形旋转一下,找到了这个平行四边形的另一组底和高,沿着高剪切,也可以把平行四边形转化成长方形。
师:这么多种方法,同学们可真是善于思考啊!老师佩服你们的数学思考能力。
师:观察原来的平行四边形和转化后的长方形,你发现它们之间有哪些等量关系?
生:平行四边形的底和长方形的长相等,平行四边形的高和长方形的宽相等,面积也相等。(贴板贴。)
师:我们观察会发现这几种方法几乎都是将平行四边形沿着高剪切开再拼成我们已经学过的图形。那是不是所有的平行四边形都可以沿着高剪拼成长方形呢?我们一起来看一看。(课件展示。)
师:果然和同学们所想的一样,平行四边形沿着高通过剪、拼、移的方法都可以转化成了我们学过的长方形,把掌声送给我们自己。
(三)推导公式
师:通过平行四边形和长方形各部分之间的等量关系你能推导出平行四边形的面积公式吗?
师:先独立想一想,然后小组内说一说推导过程。
生:因为长方形的面积和平行四边形的面积相等,平行四边形的高和长方形的长相等,平行四边形的高和长方形的宽相等,而长方形面积等于长乘宽,所以平行四边形面积等于底乘高。
师:用字母表示平行四边形的面积 S=ah。
师:这就是我们这节课要学习的平行四边形面积。(板贴课题。)
(四) 利用公式解决问题
师:现在我们用平行四边形的面积公式再来求一求这块平行四边形的花坛的面积是多少。
(师课件演示过程,并强调书写格式。先写公式,再代入数据求值。)
三、巩固练习,应用提高
(1)口算面积,对应底上的高
做一做
(2) 解决问题
(3)等底等高的平行四边形面积相等。
四、数学文化介绍
师:其实古代数学家刘徽在解决图形的面积时,就用到了我们今天所用的“剪拼”的方法,在当时叫做“割补术”。这一直是中国古代数学推导图形面积公式的传统方法。
微课介绍:刘徽,在中国数学史上有着相当重要的历史地位。他解决了一个又一个的数学难题。用割补术系统地给出了各种图形面积公式的证明。
一个平面图形由一处移至他处,面积不变。若把图形分割、移补,面积还是保持不变的。因而图形移置前后各个面积的和、差有简单的相等关系。立体图形也是这样。
这种以盈补虚出入相补的证明方式从刘徽之后,一直是中国古代数学推导图形面积公式的传统方法。
三角形、梯形的面积可不可以也利用出入相补的原理推导而来呢?这就是留给同学们课后思考的问题。
评析:
本节课,徐老师采用问题驱动的方式,巧妙设计数学探究活动,让学生经历了猜想——操作验证——推导结论的科学探究过程,很好地培养了学生推理能力和空间观念。同时,教学中能够关注学生的差异,注重启发、互动、合作交流,学生的主体地位和教师的主导作用得到体现。下面对本节课简要评析如下:
1.巧设核心问题,明晰课堂教学主线。
“问题是思维的心脏”,每一节课都要有核心的问题引领学生的数学思考,才能使课堂焕发生机活力、激活学生思维碰撞的火花。本节课中,徐老师聚焦课堂教学的重难点,巧妙设计问题串引领课堂教学主线。课伊始,徐老师引领学生从生活情境中提炼出问题:怎样比较长方形和平行四边形的面积?然后,顺应学生的思维,呈现两个操作活动:数格子和剪拼活动。再聚焦平行四边形,突出两个核心问题:如何将平行四边形转化为长方形?平行四边形和拼成的长方形有什么等量关系?这两个问题的顺利突破,为后续推导平行四边形的面积公式提供了有利保障。本节课中教师对数学问题的设计精巧,善于捕捉学生的生成,进行有效引导和追问,使课堂各环节衔接紧凑,学生活动充满浓浓的“探究味”。
2.注重策略多样化,渗透 “转化”思想。
《数学课程标准(2011版)》指出:数学课程内容要符合学生的认知规律,不仅包括数学的结果,也包括数学结果的形成过程和蕴含的数学思想方法。我們知道,平行四边形面积推导中核心的数学思想方法是“转化”思想。如何让学生自己发现并运用这一思想方法去探究平行四边形的面积是教学的难点。本节课中,徐老师为学生提供充分的探究空间,数平行四边形格数的时候,鼓励学生运用多种方法数格子。当第一个学生按照不足一格按一格数出面积后,教师追问还有没有更准确的方法。在教师的引导下,学生将平行四边形的一个角的格移到另一边,凑成一个长方形,长方形一行有6个格,有4行,就是24个满格,长方形的面积就是24平方厘米,所以平行四边形的面积也是24平方厘米。教师抓住这名学生所提到的“转化”一词,实时解读“转化”的数学思想,引导学生呈现出多种运用“转化”割补数的方法。这个环节的处理,让学生体会到直接数格子具有一定的局限性和“转化”成整格来数的优势,同时,也初步体会到长方形和平行四边形的联系,为后续探究平行四边形的面积做好铺垫。
3.丰富从“特殊”到“一般”体验,培养学生推理能力。
推理能力作为《数学课程标准(2011版)》中十个核心概念之一,是学生必须具备的数学素养。而在小学阶段,数学推理多采用举例子说理的方式,这种推理需要学生多角度举例子,通过归纳和类比才能得出一般性的结论。徐老师在验证猜想的活动中,设计了剪一剪、移一移、拼一拼的动手操作活动,引导学生呈现多种方法,验证只有沿高剪才能转化为长方形,并且利用课件动画呈现更多的例子进行体会,然后再通过观察、比较、分析得出长方形的长与平行四边形的底相等,长方形的宽与平行四边形的高相等,长方形的面积等于平行四边形的面积。在此基础上,得出一般性的结论。这个环节的设计,注重“体验”,同时关注从特殊到一般的数学推理过程,培养了学生科学严谨的精神和数学逻辑推理能力。
当然,本节课也存在一些问题。如,数格子和验证猜想这两个活动衔接不够自然,两个活动思考的问题有重复现象。建议:两个活动应该有侧重,第一个活动后,教师应该小结学生发现的数学问题。第二个活动要淡化发现等量关系,而要突出平行四边形面积中高的理解,同时要验证前面活动中发现的等量关系。
