寒区隧道衬砌冻胀力分析

李 欣， 张志强

(西南交通大学, 四川成都 610031)

[定稿日期]2017-08-29

近年来，我国寒区隧道建设增加，与一般地区相比，寒区隧道工程要解决多项复杂的技术性问题，其中最主要问题是寒区隧道冻胀作用、季节性冻融影响[1]。近年来有不少学者对寒区隧道进行了深入的研究，并取得了大量研究成果。张德华等[2]给出计算隧道冻胀力的弹性和黏弹性解析计算方法。王建宇等[3]推导了局部积水冻胀模型下隧道的冻胀力。夏才初等[4]推导了岩体冻胀率计算公式。

现有研究给出了冻胀力和冻胀率的计算方法以及冻胀力的分布规律，并未得到衬砌厚度、冻胀圈厚度、冻胀率对隧道衬砌冻胀力的影响规律。本文通过有限元软件ANSYS对矮拉山隧道断面进行热-结构耦合分析，得到衬砌厚度、冻胀圈厚度、冻胀率对隧道衬砌冻胀力的影响规律以及冻胀力作用下隧道衬砌最不利部位，为以后的隧道设计提供理论及经验数据。

1 工程背景

矮拉山隧道位于西藏江达县岗托镇国道317线上，为单线双洞隧道，隧址海拔3 970 m。隧道起点K1002+300，终点K1008+088，全长约5.788 km。隧道出入口属浅埋段，洞顶围岩属Ⅴ级围岩。

隧道地区最高气温33.4 ℃，最低气温-20.7 ℃，冻结时间为当年12月至次年2月。一般冻土深度0.85 m，最大冻土深度为1.2 m，冻结时间为当年11月中旬至次年3月。

2 弹性力学法求解冻胀力

2.1 计算假设与公式

寒区隧道的冻害是温度、重力等多场耦合作用的结果。本文计算对问题进行简化，以便求解隧道冻胀力，做出如下假设：假设隧道处于无限大的土体中，且形状为圆形；隧道围岩为二相介质且为连续各向均质同性介质；假设冻结围岩封闭饱水的弹性介质；不考虑衬砌、围岩自重。弹性力学模型[5]见图1。

Δh1=απ[(b+c)2-b2]

(1)

(2)

式中：Δh1为冻结区围岩总膨胀量；Δh2为冻结区围岩外壁膨胀量；α为围岩冻胀率。

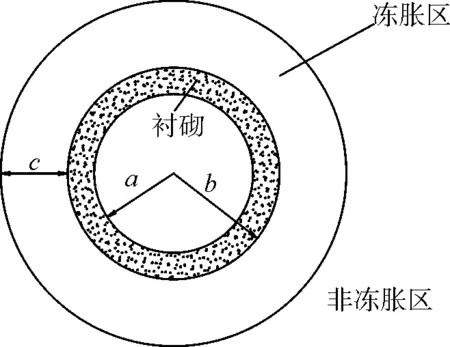
图1 冻胀力弹性力学模型

当r=b时，位移δ1为：

(3)

令A=b+h+Δh2B=(b+c+Δh2)2+b2

冻结圈内侧r=b时，位移δf1；冻结圈外侧r=b+c+Δh2时，位移δf2。

(4)

(5)

未冻结围岩内侧位移δ2为：

(6)

式中：E1、μ1为衬砌弹性模量和泊松比；E2、μ2冻结围岩弹性模量和泊松比；E3、μ3未冻结围岩弹性模量和泊松比。

(7)

求解冻胀力σ1如下：

2.2 计算结果

不同冻胀率的计算结果见表1。

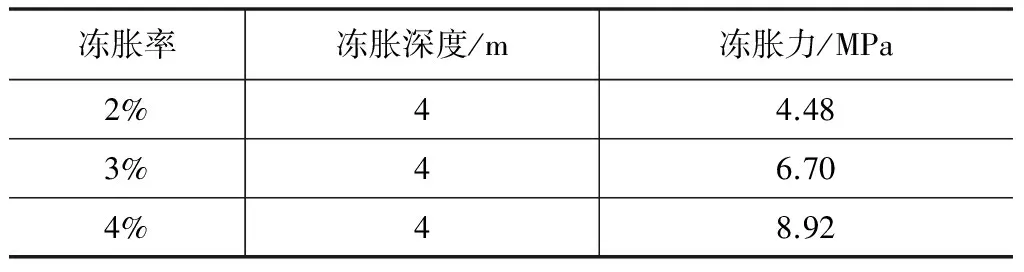
表1 不同冻胀率结果

3 温度场和冻胀力数值模拟

3.1 冻胀力的温度场耦合模型建立

弹性力学方法求解隧道冻胀力是经过一定假设和简化求得的，具有一定的局限性，不能真实的反应隧道衬砌的受力状态和变形情况，采用弹塑性模型，进一步对冻胀力进行求解。

选择地层-结构模型计算，利用ANSYS软件，选用间接耦合法分析隧道衬砌的冻胀和位移状态。

首先建立隧道衬砌、围岩冻结圈以及未冻围岩的计算模型。通过温度场分析，得到温度荷载，将此荷载施加到结构模型中，得出隧道衬砌冻胀力。模型中将冻胀率换算为线膨胀系数，查阅资料得到线膨胀系数取值大致为冻胀率的0.2倍[6]。模型网格划分及温度场分析如图2、图3所示。

图2 模型网格划分

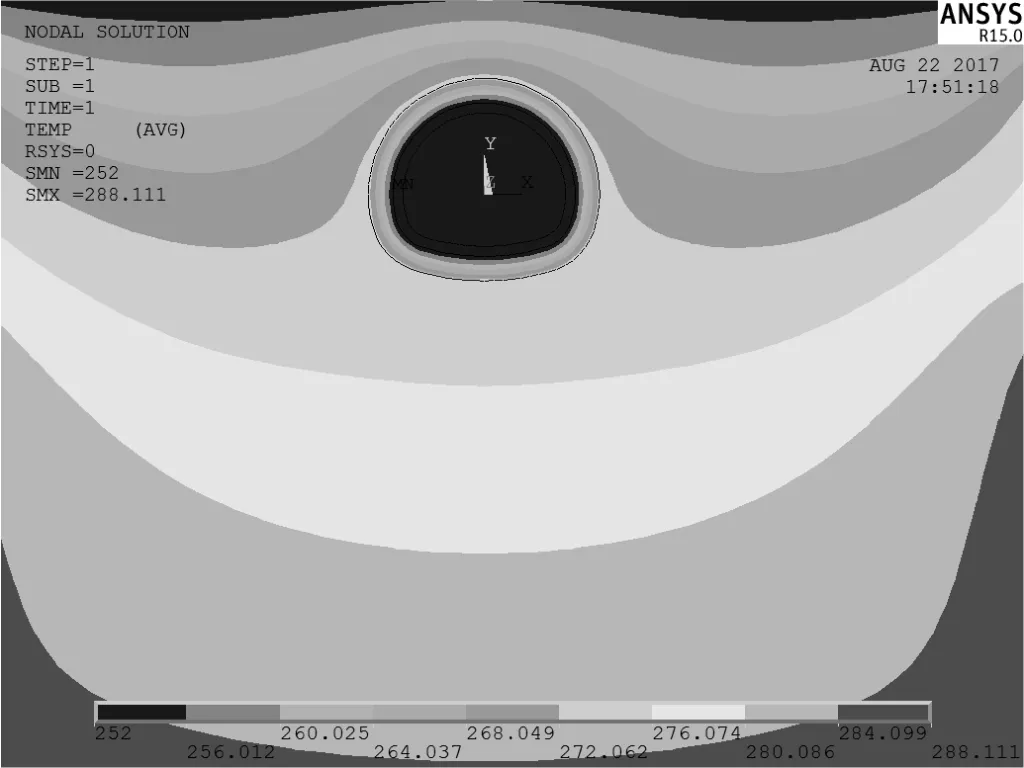
图3 温度场分析

3.2 计算参数和计算工况

通过查找规范、文献调研和实测数据等相关资料得到表2所示的围岩和衬砌的各项相关力学参数。

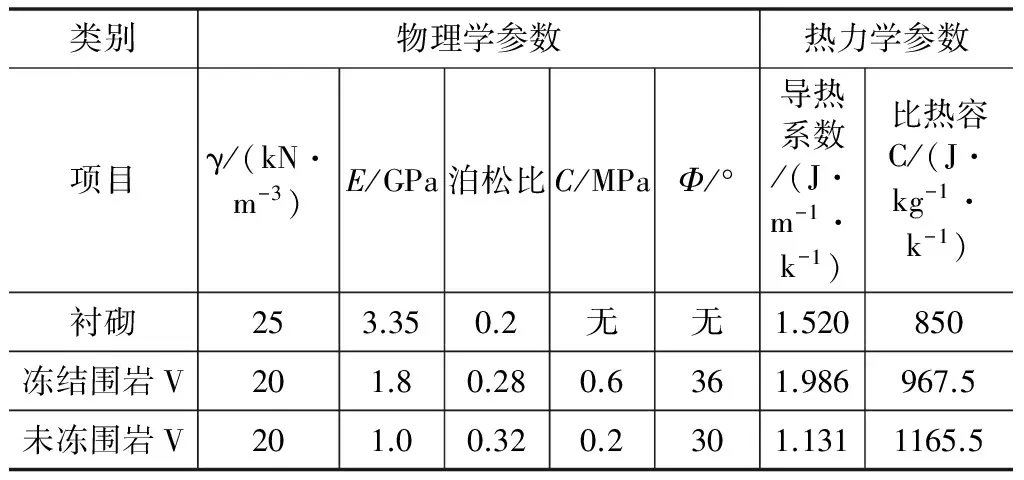
表2 围岩和衬砌的各项参数

计算工况如图4～图6所示，埋深选择10 m、20 m、30 m，冻胀深度2 m、4 m、6 m，冻胀率2 %、3 %、4 %。

(a)冻胀率2%

(b)冻胀率3%

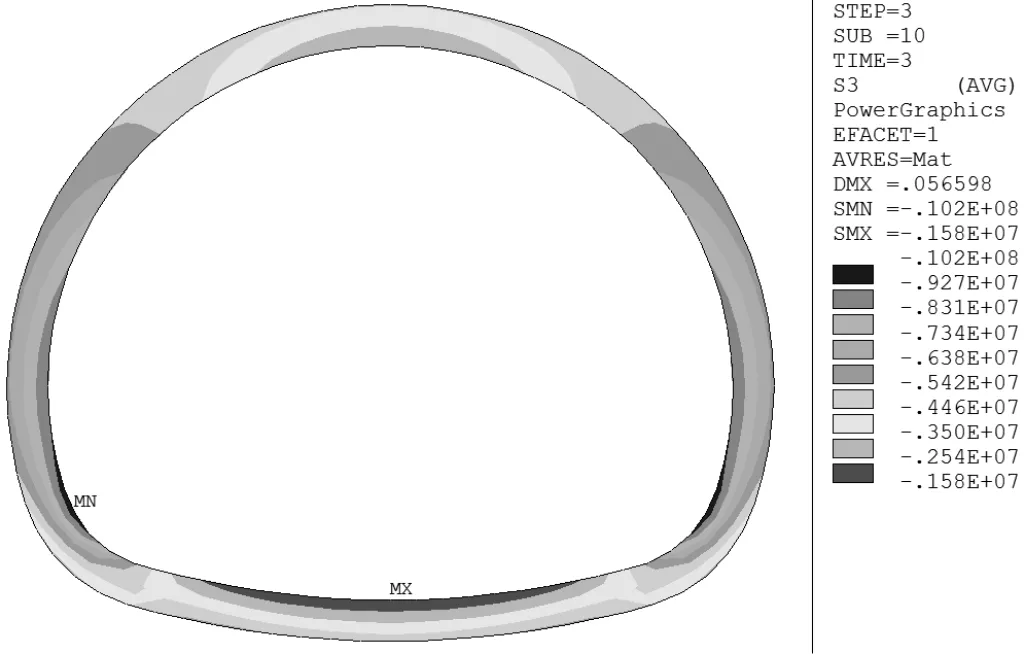
(c)冻胀率4%图4 不同冻胀率衬砌应力分布云图(单位：Pa)

(a)埋深10m

(b)埋深20m

(c)埋深30m图5 不同埋深衬砌应力分布云图(单位：Pa)

3.3 计算结果及分析

3.3.1 不同冻胀率衬砌受力分析

选取埋深20 m、冻胀深度4 m、冻胀率分别为2 %、3 %、4 %的三种工况类型，受力分析如下：

围岩自重情况下，保持隧道冻胀深度和埋深不变。由图7可以看出，隧道衬砌的应力随着冻胀率的增大而增大，最大压应力在墙脚和拱脚位置，并随着冻胀率增大逐渐从墙脚向拱脚转移。

考察冻胀作用引起轴力的结果，发现随冻胀率增大衬砌所受到轴力不断增大，最大轴力在拱脚附近。随冻胀率增大，拱顶、拱腰、拱脚和仰拱弯矩都明显变大，这是因为随冻胀率增大冻胀力变大，向内挤压衬砌结构，拱腰、拱脚、仰拱处受到较大的剪力，最大弯矩在拱腰处。

(a)冻深2m

(b)冻深4m

(c)冻深6m图6 不同冻胀深度衬砌应力分布云图(单位：Pa)

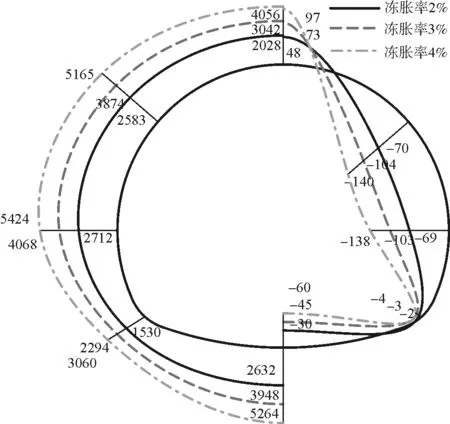
图7 冻胀率对衬砌轴力(单位：kN)、弯矩(单位：kN·m)影响

3.3.2 不同埋深衬砌受力分析

选取冻胀率2%、冻胀深度4 m、埋深分别为10 m、20 m、30 m的三种工况类型，受力分析如下：

围岩自重情况下，保持隧道冻胀深度和冻胀率不变。由图8可以看出，隧道衬砌的应力随着埋深的增大而增大，这是由于自重效应对衬砌压力的作用，最大压应力出现在墙脚和拱脚位置。

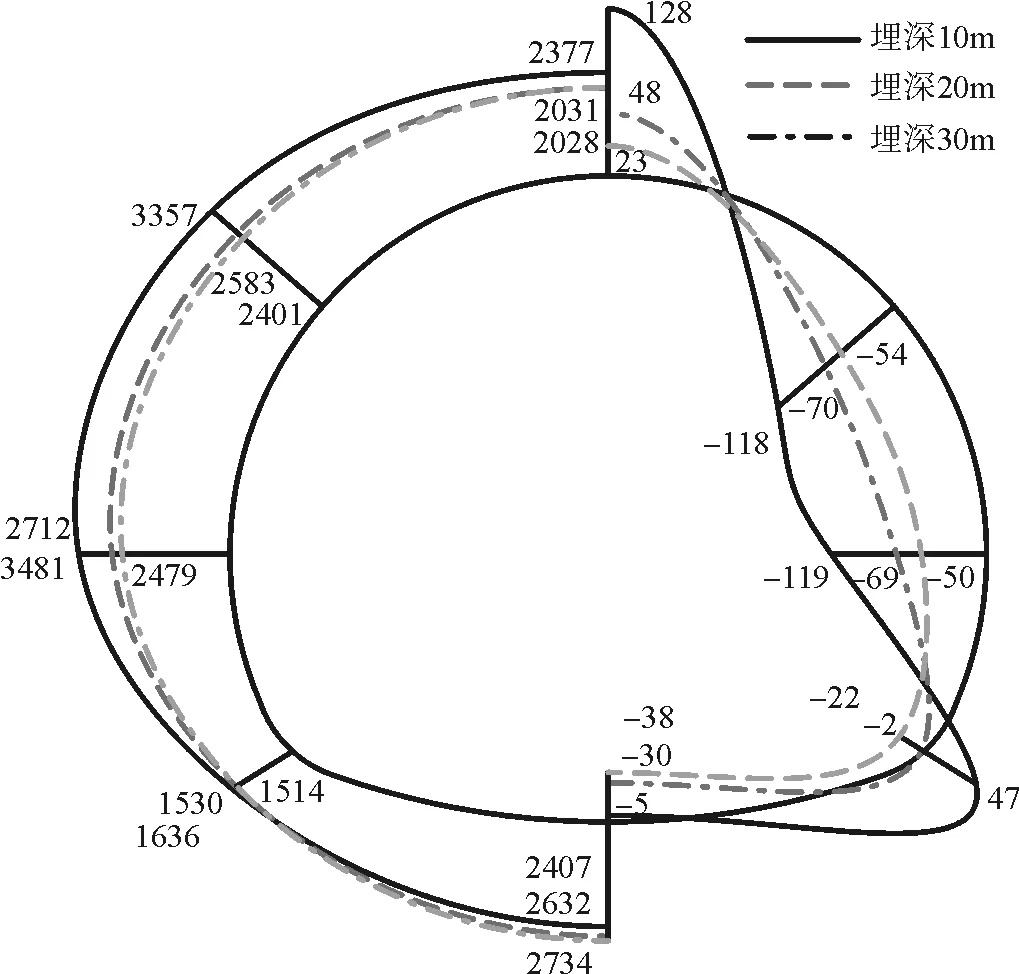
图8 埋深对衬砌轴力(单位：kN)、弯矩(单位：kN·m)影响

考察冻胀作用引起轴力、弯矩结果，发现随埋深增大衬砌拱顶、拱腰、拱脚所受到轴力、弯矩不断减小，但随埋深增大减小幅度显著降低。由于冻胀力的变化在此只受到温度场变化的影响，随埋深增大地表低温对衬砌结构作用降低，到达一定埋深后对结构不再产生影响。

3.3.3 不同冻胀深度衬砌受力分析

选取冻胀率2 %、埋深20 m、取冻胀深度分别为2 m、4 m、6 m的三种工况类型，受力分析如下：

考虑围岩自重，如果隧道埋深和冻胀率不变，由图9可以看出，隧道衬砌的应力随着冻深的增大而增大。这是由于冻胀围岩厚度增大围岩膨胀产生应变变大，在围岩挤压下使衬砌圈承受剪应力增大，进而使衬砌圈环向压应力变大，最大压应力出现在墙脚和拱脚位置。

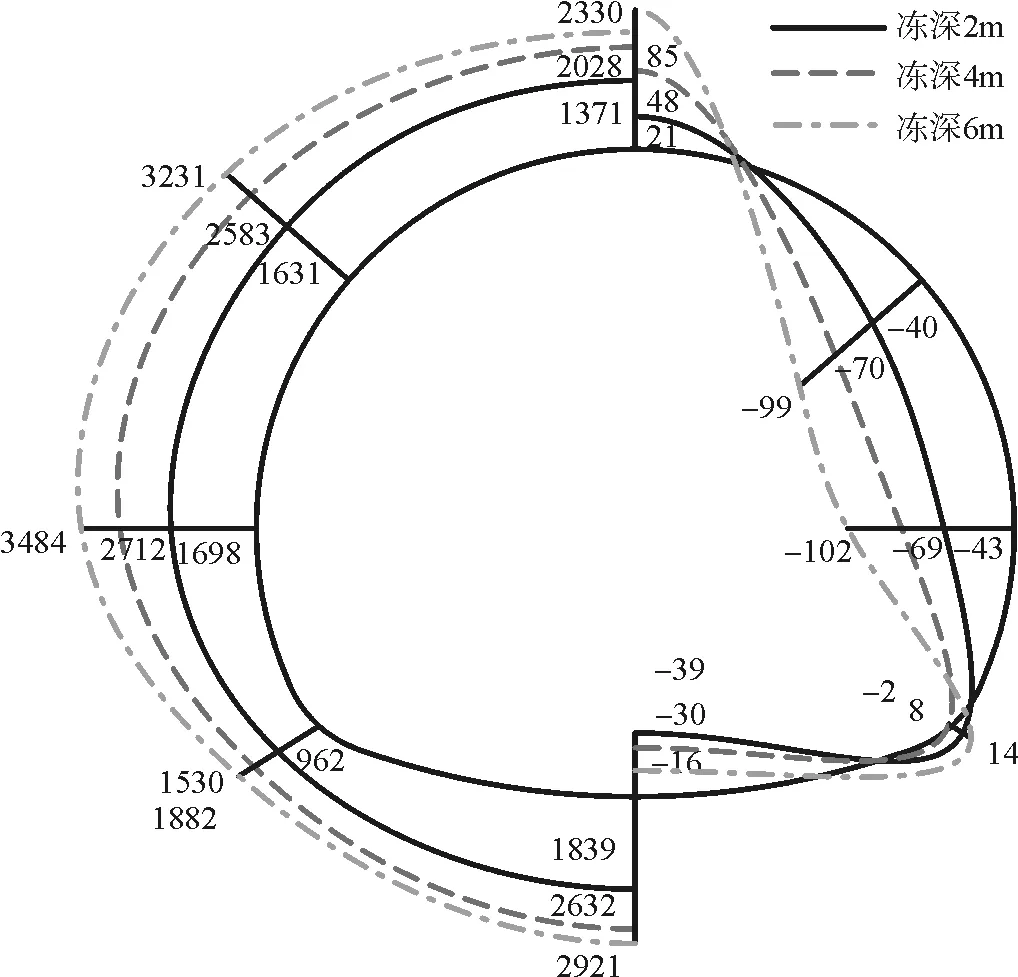
图9 冻胀深度对轴力(单位：kN)、弯矩(单位：kN·m)影响

提取冻胀作用引起衬砌的弯矩、轴力，考察比较轴力图结果可知，发现随冻深增大衬砌轴力不断增大，最大轴力在拱脚附近。比较弯矩图，发现随着冻深增大衬砌所受弯矩明显增大，最大弯矩在拱脚处，达到102 kN·m。

4 结论

(1)不同冻胀率下，弹性力学方法和数值模拟计算冻胀力对比分析结果如表3所示。可见两种计算结果的规律存在高度一致。

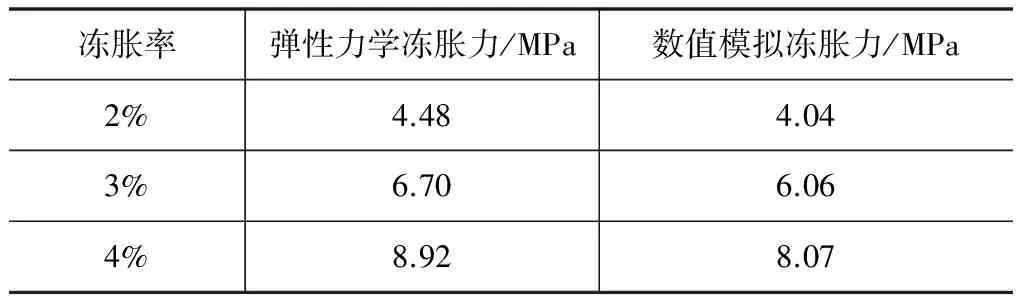
表3 数值计算与弹性力学结果对比

(2) 隧道衬砌应力随着冻胀率、冻胀深度增大而增大，最大压应力在墙脚和拱脚位置。随冻胀率、冻胀深度增大，拱顶、拱腰、拱脚和仰拱所受冻胀力都明显变大，最大冻胀力在拱脚附近。

(3) 隧道衬砌应力随着埋深的增大而增大，最大压应力出现在墙脚和拱脚位置。随埋深增大，衬砌拱顶、拱腰、拱脚所受到冻胀力不断减小，但随埋深增大减小幅度显著降低。

冻胀力作用下，隧道衬砌薄弱部位主要集中在拱脚位置，其次在拱腰处，针对以上部位需加以重点设防。

[1] 谭贤君. 高海拔寒区隧道冻胀机理及其保温技术研究[D].中国科学院研究生院(武汉岩土力学研究所),2010.

[2] 张德华,王梦恕,谭忠盛,等. 风火山隧道围岩冻胀对支护结构体系的影响[J]. 岩土工程学报,2003(5):571-573.

[3] 王建宇,胡元芳. 隧道衬砌冻胀压力问题研究[J]. 冰川冻土,2004(1):112-119.

[4] 夏才初,黄继辉,韩常领,等. 寒区隧道岩体冻胀率的取值方法和冻胀敏感性分级[J]. 岩石力学与工程学报,2013(9):1876-1885.

[5] 耿珂. 冻融循环对寒区隧道结构冻胀力的影响[J]. 冰川冻土,2013(4):913-919.

[6] 王洪存. 冻土隧道冻胀力敏感度分析及防冻保温技术研究[D].重庆交通大学,2014.