基于三角级数法合成多维多点非平稳地震动

周刘茜, 郑史雄, 陈 航

(西南交通大学桥梁工程系, 四川成都 610031)

[定稿日期]2017-08-14

地震动输入一直是处于地震工程学中的一个研究热点，对于平面尺寸较大的大跨度桥梁结构，若采用一致激励对桥梁结构进行抗震计算，不能完全考虑结构的空间相关性，因此采用多点输入是必要的。且地震波数量的有限性、随机性和不确定性等限制了多点直接动力分析法应用到实际工程中，因而模拟生成具有特性参数的多点地震动是地震工程学领域的研究热点。

关于地震动合成研究，Hao[1]等基于单点人工地震波合成，通过分解多点构成的互功率谱矩阵，并假定相位角呈均匀分布，合成了多点人工地震动时程；Ramadan[2]提出了两种地震波合成方法，考虑了地震动的非平稳性，对比了两种方法的适用条件和计算效率，应用到了单跨和多跨简支梁分析中；江近仁[3]、汪梦甫[4]、徐强[5]、牛志国[6]、邢超宇[7]和黄朝光[8]等研究了人工地震波合成技术，为多点激励地震波的合成奠定了基础，为准确的结构抗震分析提供了必要条件。

本文基于随机振动理论，将一维多点激励地震波的合成理论扩展成为多维多点地震波合成，考虑了地震动的空间效应和非平稳性，通过迭代计算修正幅值提高计算精度，所合成多维多点地震波更能表征实际地震动的特性，便于工程应用。

1 地震动合成与修正公式

1.1 合成公式

基于随机振动理论，将合成单点地震动扩充到合成多点地震动，并考虑空间变异性、空间效应和场地条件。其合成方法采用三角级数法。

(1)将反应谱转换为当量功率谱。

(1)

式中：S(ω)为功率谱；Sa(ω)为目标反应谱；T为持续时间；ω为固有频率；ξ为阻尼比；r为反应不超过反应谱值得概率。

(2)用三角级数迭加法生成零均值的平稳高斯过程。

(2)

(3)将平稳时程乘以非平稳强度包线得到非平稳加速度时程。

a(t)=f(t)·X(t)

(3)

强度包线函数可取为以下形式：

(4)

式中：t1为地震动时程上升段时间；t2为下降段起始时间；c为衰减系数。

1.2 修正公式

初次计算得到的地震动时程转换的反应谱，一般近似于目标反应谱。为了提高精度，此时对合成地震时程采用频域方法进行迭代修正[9]。

(1)人工地震动时程生成反应谱R(ω,ζ)，计算公式为[10]：

(5)

式中：h()为单位脉冲响应函数。

(2)人工地震动时程幅值修正，每一个频率点处人工地震波值，以人工反应谱和目标反应谱的比值作为验证精度值，当精度值不满足拟合精度值时，进行幅值调整，调整后再次生成人工地震动，并将新人工地震动生成相应反应谱，再与目标反应谱比较，进行精度值检验和调整。如此反复，直至达到精度要求，即拟合精度迭代计算[10]。

(6)

按式(7)对幅值进行调整：

(7)

2 合成多维多点非平稳地震动

本文以某斜拉桥为例，按以上方法采用拟合反应谱法合成多维多点非平稳地震动。将反应谱转换为当量功率谱，并作为支撑处地震激励的自功率谱，然后利用三角级数法初次计算得到多维多点非平稳地震动。

第一次生成多点非平稳地震动时程的拟合反应谱与目标反应谱有一定的差别，为了使拟合误差到达精度要求，通过式(6)、式(7)对幅值谱进行调整生成修正后的幅值谱，并结合相位谱生成地震动时程，迭代计算后的最终拟合反应谱如图1所示。

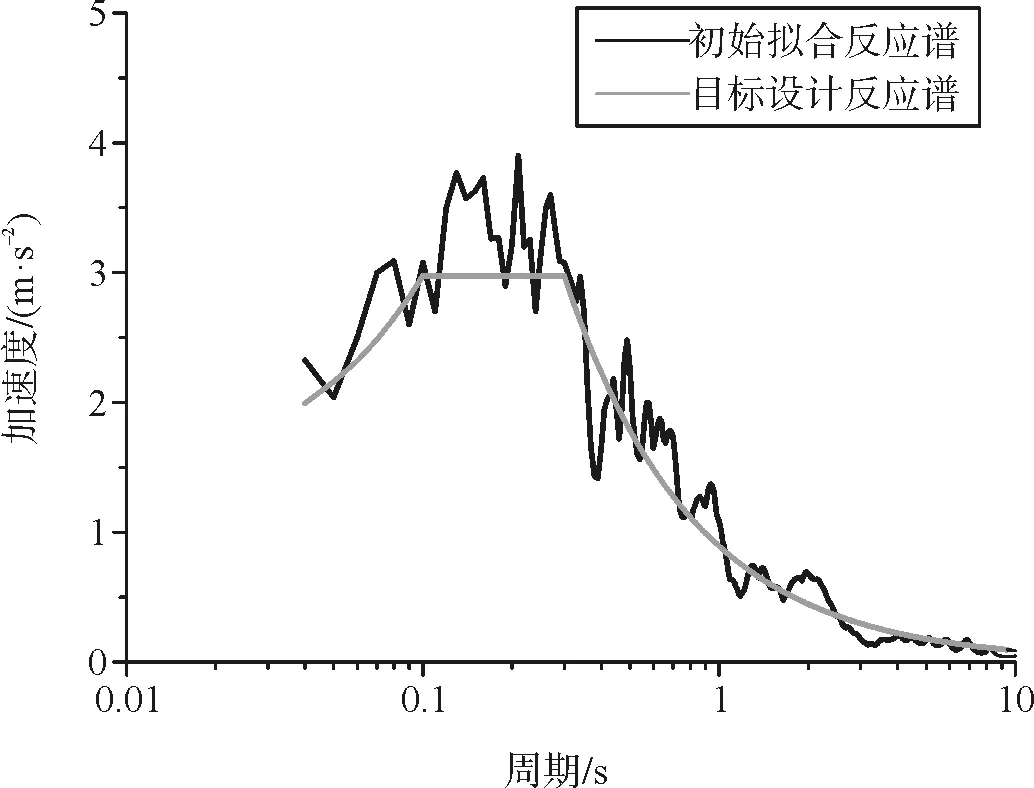
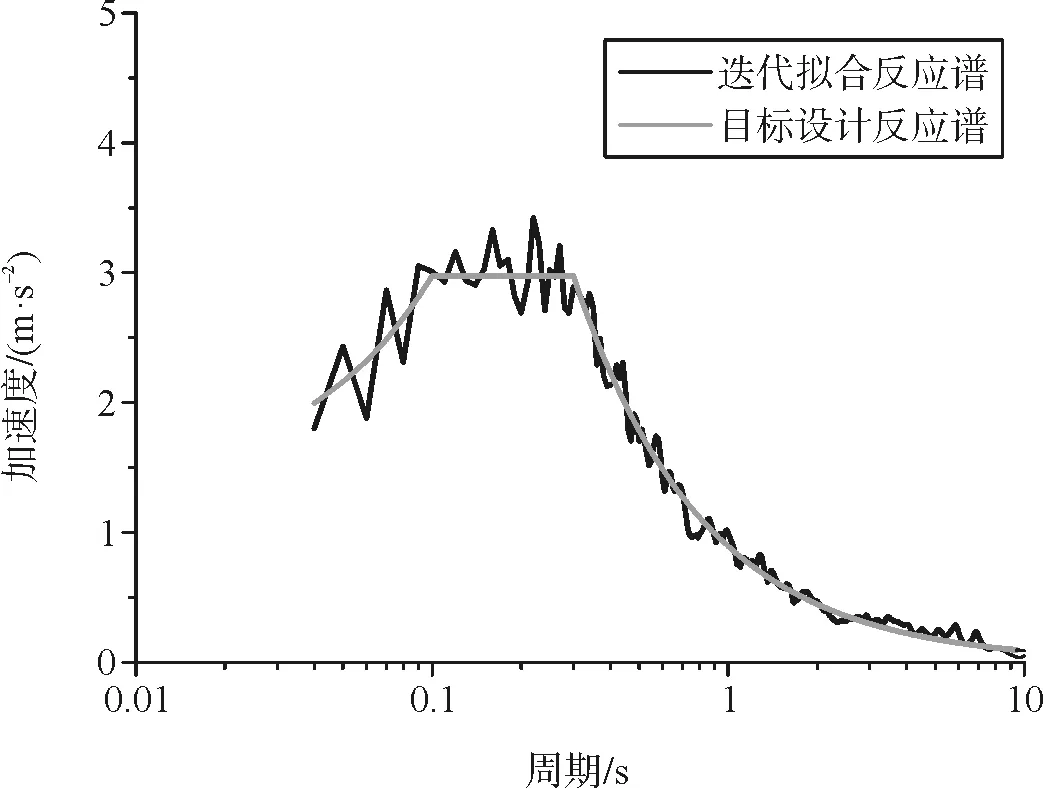
图1 初始和修正的非平稳拟合反应谱

其拟合设计反应谱修正的空间多点非平稳地震动如图2所示。

图2 迭代拟合的非平稳地震动

3 合成地震动验证

为了验证本文人工合成地震动的准确性，用本文合成的地震动和实际地震动对结构响应进行对比分析。实际地震动记录的选取利用PEER网站来选取合适的地震波。该网站的首页为：http://peer.berkeley.edu/peer_ground_motion_database。

3.1 计算模型简介

以某西部山区高墩刚构桥梁为背景，桥梁布置为89 m+168 m+89 m，两个墩高分别76 m和103 m。在墩底施加上述基于三角级数拟合合成的地震动时程，并与在墩底施加实际的RSN81_SFERN_PPP000地震动时程进行响应对比。刚构桥梁示意图如图3所示，三维有限元数值模型如图4所示。

图3 连续刚构桥示意

图4 有限元数值模型

该刚构桥梁采用一致激励时程分析法计算，即1号墩和2号墩加载的地震动相同，计算基于三角级数和实际地震动时程的桥梁响应。为了更明确验证结构响应结果，只对纵桥方向添加地震动时程。

3.2 响应结果对比分析

以ANSYS为计算平台，对本文合成的地震动和实际地震动加载的刚构桥梁进行响应分析。取时程响应的最大值为研究对象，响应结果如图5～图7所示。

(a) 主梁纵向位移

(b) 1号桥墩纵向位移

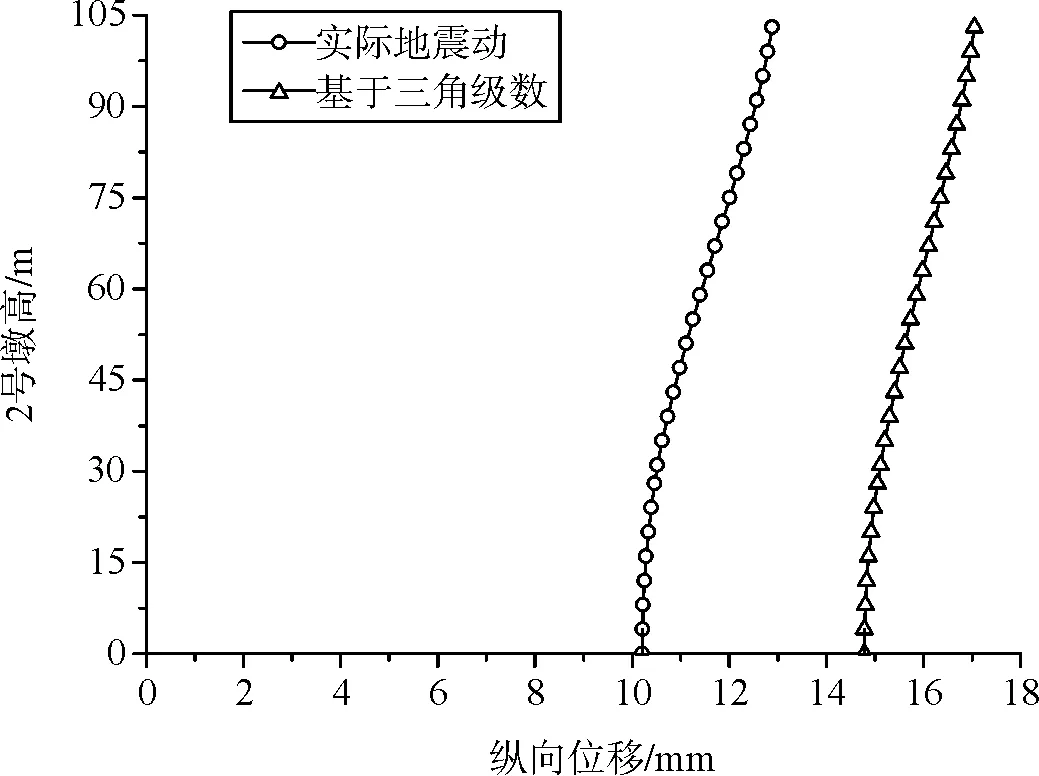
(c) 2号桥墩纵向位移图5 纵向最大位移响应

从图5～图7可以得到如下验证结论：(1)主梁和桥墩的位移、剪力和弯矩响应在两种地震动下响应规律一致；(2)主梁及墩的位移响应在两种地震动下差距较为明显，基于三角级数合成地震动下比实际地震动下大5 mm，而剪力响应和弯矩响应相差不大，在墩底处基于三角级数合成的地震动要大一些。

(a) 1号桥墩纵向剪力

(b) 2号桥墩纵向剪力图6 纵向最大剪力响应

(a) 1号桥墩纵向弯矩

(b) 2号桥墩纵向弯矩图7 纵向最大弯矩响应

通过以上的时程响应计算分析，以基于三角级数人工地震动和地震动RSN81_SFERN_PPP000地震动的反应谱大致相似为前提，其纵向的位移、剪力和弯矩响应分布规律基本一致，且数值上相差不大。因此说明了本文合成的人工地震动时程具有实际地震动的相应特性，能如实际地震动一样用于结构计算且响应值准确可靠。

4 结论

本文基于三角级数法这一地震动合成方法合成一非平稳 地震动，再利用设计反应谱拟合法对其幅值谱进行调整生成修正后的谱，并结合相位谱生成地震动时程。对比分析了合成的人工地震动和基于PEER地震动数据库选取的地震动作用下高墩钢构桥梁结构的响应，得出以下结论：

(1) 理论上讲，多维多点非平稳地震波合成比一维多点激励地震波的合成更符合实际地震动特性，为大跨度结构抗震分析提供更实际的地震动输入；

(2) 合成的多维多点非平稳人工地震动时程通过拟合反应谱的方法进行幅值修正，得到了满足精度的非平稳地震动时程，为结构地震动时程的响应分析提供了正确的地震动输入保障；

(3) 合成多维多点地震波克服了实测地震波有限的缺点，为桥梁抗震规范多维多点抗震分析提供了多维地震波合成的理论依据；

(4) 基于PEER地震动数据库选取的地震波和人工合成地震动作用下高墩刚构桥梁结构的响应，说明了本文所合成的人工地震动时程具有实际地震动的相应特性，能如实际地震动一样用于结构计算且响应值准确可靠。

[1] Hao H, O liveira C S, Penzien J. Multiple-station ground motion processing and simulation based on SMART-1 array data [J]. Nuclear Engineering and Design, 1989, 111(3)：293 -310.

[2] Ramadan O, Novak M. Simulation of spatially incoherent random ground motions [J]. Journal of Engineering Mechanics. 1993, 119(5)： 997-1016.

[3] 江近仁，洪峰. 功率谱与反应谱的转换和人造地震波[J]. 地震工程与工程振动. 1984， 4(3): 1-11.

[4] 汪梦甫，尹华伟，周锡元. 从反应谱求功率谱的精确方法及其应用[J]. 地震工程与工程振动， 2004，24(2): 53-58.

[5] 徐强，陈健云，李静. 基于小波理论合成人工地震波[J]. 振动与冲击， 2009， 28(8): 180-183.

[6] 牛志国，李同春，王亚莉. 基于水工设计反应谱的人工地震波合成[J]. 河海大学学报：自然科学版， 2007，1(3)：262-266.

[7] 靳超宇，廖旭. 辽河特大桥项目空间相关多点地震动合成研究[J]. 防灾减灾学报， 2010，26 (2)：1-5.

[8] 黄朝光，彭大文. 人工合成地震波的研究[J]. 福州大学学报： 自然科学版， 1996，2(4)：84-90.

[9] 胡聿贤,何训.考虑相位谱的人造地震动反应谱拟合 [J].地震工程与工程振动,1986, 6(2)：37-51.

[10] 江近仁，洪峰.功率谱与反应谱的转换和人造地震波[J].地震工程与工程振动, 1984, 4(3)：1-11.