薄壁零件压力铸造控制方法研究及鲁棒性分析

李 拓，邢小军

(1.中国飞行试验研究院，西安 710089; 2.西北工业大学 自动化学院， 西安 710029)

0 引言

复杂薄壁零件一般由几个平面和曲面构成，壁厚小于4 mm局部为0.5 mm，要求精度高，铸造成形难度大[1]。但它的用途却十分广泛，在国民经济以及军事领域具有十分重要的意义和应用价值。在电子、汽车行业尤其是航空航天以及兵器领域中越来越重要，因此研究一套铸造设备成为一个急需解决的问题。传统的零件铸造方法主要是手工铆接、手动控制，无法满足复杂的压力铸造工艺曲线，铸造的零件精度和性能比较差，达不到技术指标。

本文设计的TY-3压力铸造计算机控制系统，通过计算机控制压力按照理想压力曲线进行整个零件铸造过程，控制精度高，与理想压力曲线比较接近，铸造的零件能达到技术指标。压力铸造主要包括：低压铸造，调压铸造，真空吸铸。低压铸造是使液体金属在压力作用下充填型腔，以形成铸件的一种方法；调压铸造是指先进行抽真空使上下腔压力达到铸造所需的条件，然后向上下压腔中通入压缩气体，利用上下腔压差使金属液通过升液管进入型腔，最后凝固形成零件的过程[2]；真空吸铸是一种在型腔内造成真空，把金属由下而上地吸入型腔，进行凝固成形的铸造方法。

本文针对压力铸造系统模型进行控制方法研究，采用PID、DMC、PID+DMC控制算法进行仿真，对结果进行比较进而验证三种算法的控制效果，并对系统中可能出现的模型失配问题进行分析，验证算法的鲁棒性。

1 压力铸造系统数学模型

TY-3压力铸造计算机控制系统主要由计算机控制系统和压力铸造气路系统两大部分(压力罐和真空泵均归入到气路系统)组成。其中压力铸造气路系统主要是压力罐、真空泵、电磁阀、调节阀、上下压腔的连接，计算机控制系统是上下位机与硬件结构的连接。工作原理为：根据设定的上、下压腔铸造理论工艺曲线，由计算机控制系统输出的电气信号驱动气路系统中相应的电磁阀和调节阀工作，通过电磁阀的开关动作控制气路系统中压缩空气的通断，通过调节阀开度的变化调节进入上、下压力腔中压缩空气的流量，最终使上、下腔中的压缩空气的压力跟随设定的理想曲线进行变化。

铸造过程中上位机与下位机同时采集6路压力信号以及8路报警信号，来确保铸造过程的可靠性和安全性。同时上位机还要采集22路温度传感器测得的上下腔各个点处的温度来保证系统正常工作；其中4路比例气动调节阀形成推挽式控制器控制上下腔压力，13路电磁阀控制气路结构系统中各个点处的开关状态，完成整个铸造工艺流程。

压力铸造系统模型主要包括上压腔模型和下压腔模型，由于上压腔模型与下压腔模型比较类似，本文以上压腔模型为例进行研究。图1为压力铸造系统上压腔数学模型。

图1 上压腔模型

其中:P01是上压腔的期望压力，P1是上压腔的实际输出压力，K01是上压腔压力与电压的比例系数，Q1是上压腔气体的流量。

压力铸造系统上压腔模型主要由比例调节阀、上压腔、压力传感器组成。在TY-3压力铸造计算机控制系统中，铸造设备的执行机构采用一个气动薄膜调节阀与一个比例阀组装成了一个比例气动调节阀，它的主要作用是：通过控制器调节输出电压改变比例调节阀的开度，比例调节阀开度的改变引起压缩气体流量的改变，比例调节阀模型是纯滞后的一阶惯性环节；上压腔主要用于放置铸件型腔，压力铸造过程中通过上下压腔产生压差将金属液以高速填充入型腔并凝固，从而形成零件，压力铸造系统的上压腔模型是一个积分环节；压力传感器选用的是测量范围为-0.10～0.10 MPa，相应的电压范围为1～5 V。

利用理论分析法和测试法对压力铸造系统上压腔进行建模，得到系统的传递函数为：

(1)

2 压力铸造系统控制器设计

在不加控制器的情况下，对压力铸造系统上压腔模型进行仿真，可以看出上压腔振荡比较大，稳态值为1，最大超调量为0.7，调节时间为9.2 s。

上压腔系统的动态性能比较差，不能达到要求，为了提高压力铸造系统的动态性能，下面分别用PID、DMC、PID+DMC算法进行比较来讨论这三种控制算法对压力铸造系统上压腔动态性能的影响。

2.1 PID控制

用Simulink的PID Controller模块中的PID Tuner对PID参数进行调节，得到控制参数P、I、D、N分别为0.1118、0.0011、0.1174、2.0145。压力铸造系统上压腔模型通过PID控制修正后，可以看出相对修正之前动态性能有一定的改善，仿真结果表明超调量为10%，调节时间为4.5 s，超调量有一定的改善，调节时间相对缩短，仍不能满足指标要求。

2.2 DMC控制

DMC是一种基于系统模型阶跃响应的预测控制算法，主要用于渐近稳定的线性系统[3]。

DMC算法包含以下三个部分：

1) 预测模型：对于动态矩阵控制来说，首先应该测得被控对象的阶跃响应曲线的采样值ai=a(iT)，i=1,2，…，其中T是采样周期时间[3]。对于稳定的系统，阶跃响应曲线在经过时间tN=NT后将趋向于稳定，用采样值构成的模型向量a=[a1，a2，…aN]T，N为建模时域。针对压力铸造系统上压腔数学模型，取T为0.2 s，N为50，NT=10 s后系统接近稳态值，实时仿真可得模型向量a=[ 0.03 0.2，…1 1.02]。

在优化性能指标中加入软约束条件。则k时刻的优化性能指标：

(2)

其中：qi为跟踪误差;rj为控制量变化的抑制。

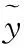
(3)

可以得到最优值△u(k)，…，△u(k+M-1)。实际的控制输入u(k)=u(k-1)+△u(k)，下一时刻求△u(k+1)，这就是滚动优化策略[3]。

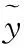
(4)

其中：

dT=cT(ATQA+R)-1ATQ=[d1…dP]

(5)

误差权阵：Q=diag(q1,…,qP)

控制权阵：R=diag(r1,…,rM)

dT为控制向量，cT=[1 0 … 0]M。如果控制策略P、M、Q、R确定，dT可以由式(3)离线一次算出，通过式(2)可以求出控制律△u(k)[4]。

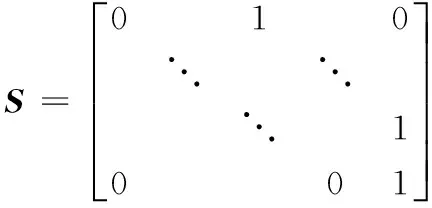
压力铸造系统上压腔控制设计时，取P为20，M为6，Q中的元素qi=1,i=1...20,R中的元素ri=0,i=1...6。以最优序列的首元素ΔuM1作为下一步控制输入增量，则下一步控制量为uM=ΔuM1+uM。动态矩阵A为：

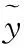
(6)

误差信息主要是对模型中的不确定性因素进行补充，但对产生的误差缺少因果联系，只能用时间序列方法进行描述。可以用加权e(k+1)的方法来修正未来的输出预测值：

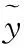
(7)

因为时间基点的变动，k+1时刻预测的未来时间点将移到k+2、k+3、…、k+N+1，k+1时刻的初始预测值通过校正后的预测向量移位后才能得到。

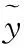
(8)

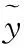
(9)

压力铸造系统上压腔模型控制设计时校正向量h1=1,hi=0.001,i=2,...,50，h=[1 0.001 ... 0.001]T。

动态矩阵控制算法是对于每个采样时刻，未来P个时刻的初始预测输出yP0(k)与期望输出ωP(k)得到的误差向量与控制向量dT点乘得到控制增量△u(k)。一方面控制增量通过数字积分运算得到控制输入u(k)作用于对象，另一方面与模型向量相乘得到预测输出yN1(k)。将实际输出y(k+1)与预测输出y1(k+1|k)比较得到误差e(k+1)，求出校正后的预测输出ycor(k+1)，移位后得到yN0(k+1)。z-1表示时间基点后退一步，整个控制过程就是这样在线反复进行。

4)DMC仿真结果分析:针对压力铸造系统上压腔数学模型，根据DMC参数设计原则可知，取T=0.2 s，N=50，可以满足ai≈as(i>N)。优化时域P至少使a(t)经历一个振荡周期，包含主要的动态特性，取P=20。由于对象为S形振荡曲线，所以取M为6满足压力铸造系统动态性能。可令R=0，Q=I，通过仿真结果表明，超调量为4%，调节时间为2.2 s，DMC算法的控制效果相对PID算法比较好。

2.3 PID+DMC控制

PID+DMC是指PID控制与被控对象串级连接，DMC控制对PID控制的结果再次进行控制的方法。首先保持PID控制参数不变，然后用DMC算法进一步控制。根据DMC参数设计原则可知，取T=0.1 s，N=40，P=30。经过PID修正后的曲线是简单的S型曲线，所以取M为2满足压力铸造系统动态性能。可令R=0，Q=I，通过仿真结果表明，超调量为1%，调节时间为1.9 s，对于PID和DMC算法来说，PID+DMC算法的控制效果比较理想。

3 仿真结果及鲁棒性分析

3.1 三种控制算法仿真结果

对于压力铸造系统上压腔模型，通过以上三种控制算法进行matlab仿真，结果如图2所示。

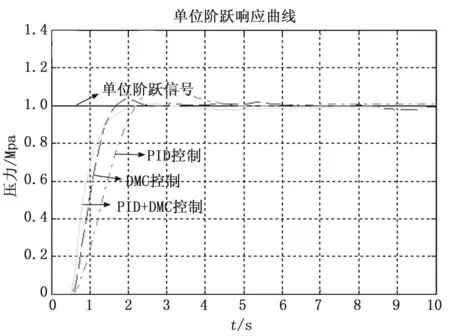
图2 PID、DMC、PID+DMC输出响应比较

三种控制算法动态性能如表1所示。

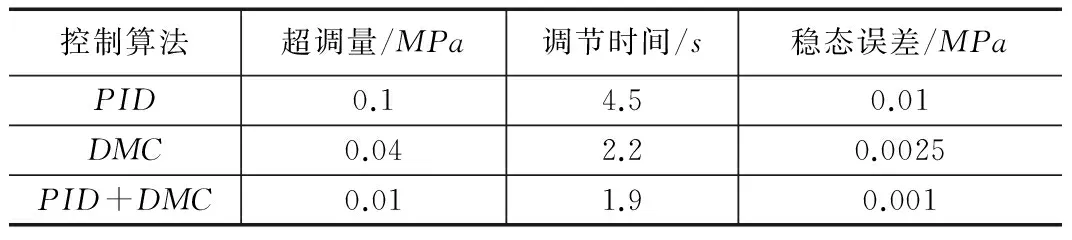
表1 三种控制算法动态性能

通过对三种控制算法进行仿真，由上表得PID+DMC算法的超调量、调节时间和稳态误差明显小于其它两种控制算法，控制效果最优[5]。在压力铸造系统中，理论输入压力曲线和实际采集压力曲线比较接近，压力误差在容限范围内，满足铸造工艺要求。

3.2 三种控制算法鲁棒性分析

由于系统辨识过程中可能参数不准确，或者模型参数发生时变，或因模型中存在非线性因素的原因，压力铸造系统的理论模型与实际系统可能在模型的幅值、阻尼、频率方面存在不匹配情况，为了更好地应用于压力铸造系统，下面研究PID、DMC、PID+DMC算法对模型失配问题的鲁棒性[6]。

由于纯滞后环节对输入输出的数值没有影响，只是时间上有一定的滞后。因此，在压力铸造模型控制算法鲁棒性分析时，仅对压力铸造系统上压腔数学模型的线性传递函数进行分析，不考虑纯滞后环节。压力铸造系统上压腔闭环传递函数为：

Φ11(s)=

(10)

其闭环单位阶跃响应为：

a1(t)=

1-e-0.32872tcos(2.78852t)-0.11788e-0.32872tsin(2.78852t)

(11)

改写为下式：

a11(t)=1-A1e-D1tcos(ω1t)-A2e-D2tsin(ω2t)

(12)

压力铸造系统在建模时可能在幅值、阻尼、频率方面有一定偏差，导致模型失配。为了使控制算法更好地应用于压力铸造系统中，下面分析幅值、阻尼和频率偏差在一定范围内三种控制算法的鲁棒性问题。

表2是模型在幅值、阻尼、频率失配的情况。

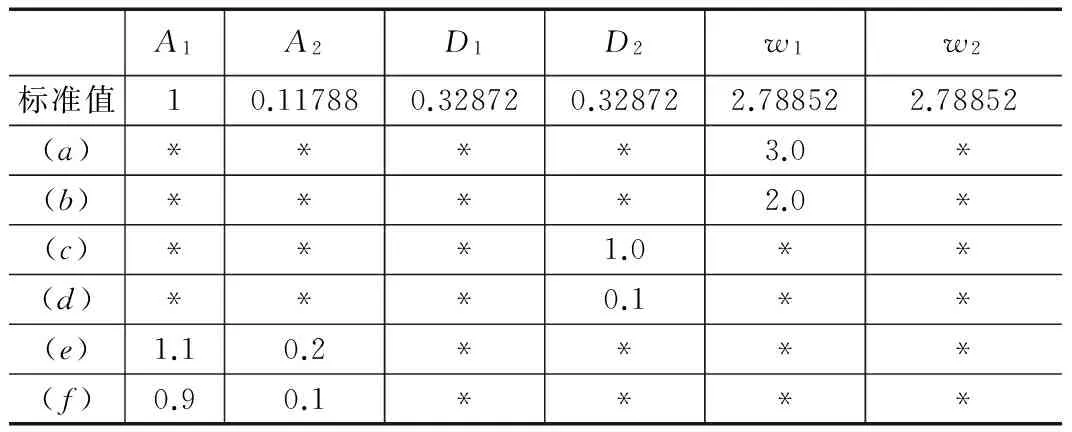
表2 模型失配

其中：*表示取标准值。

PID、DMC、PID+DMC算法鲁棒性的仿真如图3所示。

图3 PID、DMC、PID+DMC算法鲁棒性

从图3(a)可以看出，当出现模型频率失配(a)这种情况时，频率失配比较小，压力铸造系统上压腔仍能保持稳定，与最佳状态相差不大。DMC控制效果变差，PID和PID+DMC与失配前相差不大，PID+DMC算法的超调量和调节时间都小于另外两种算法，控制效果最好，具有一定的鲁棒性。

从图3(b)可以看出，当出现模型频率失配(b)这种情况时，频率失配相对比较大，压力铸造系统上压腔仍能保持稳定，与最佳状态相差比较大。三种控制算法和失配前相比变差，对比发现PID+DMC算法的超调量和调节时间最小，鲁棒性比较好。

从图3(c)可以看出，当出现模型阻尼失配(c)这种情况时，阻尼失配相对比较大，但三种控制算法和失配前相比变化比较小，三种控制算法都有一定的鲁棒性。

从图3(d)可以看出，当出现模型阻尼失配(d)这种情况时，阻尼失配比较小，三种算法和失配前相比控制效果基本没有变化，三种控制算法都有一定的鲁棒性。

从图3(e)可以看出，当出现模型幅值失配(e)这种情况时，幅值失配比较小，三种控制算法和失配前相比都有一定的变化。PID+DMC和PID调节时间较长，DMC超调量较大，三种算法仍能保持压力铸造系统上压腔稳定工作。

从图3(f)可以看出，当出现模型幅值失配(f)这种情况时，幅值失配比较小，三种控制算法和失配前相比控制效果变化比较小，PID+DMC和DMC控制效果比较好，都有一定的鲁棒性。

综上所述，三种控制算法对压力铸造系统模型阻尼失配时，控制效果和失配前相比基本不变，鲁棒性较好；对频率失配较大时，三种控制算法控制效果变差，相对来说PID+DMC鲁棒性较好，仍能保持压力铸造系统稳定工作；当幅值失配时，三种算法控制效果变化比较小，都有一定的鲁棒性。综合考虑PID、DMC、PID+DMC控制算法对压力铸造系统上压腔模型的失配问题，可以得出PID+DMC算法对模型失配的鲁棒性比较好。

从对压力铸造系统上压腔模型的动态性能和鲁棒性总体考虑，可以得出PID+DMC算法具有明显的优势。

4 结论

本文针对TY-3压力铸造计算机控制系统进行建模分析，采用PID控制、DMC控制和PID+DMC控制三种控制方法进行控制器的设计，并在Matlab/Simulink环境下进行了仿真。仿真结果表明三种方法均实现了压力铸造系统的稳定控制，通过不断地对参数进行修正比较使TY-3压力铸造系统的动态性能达到了满意的效果，得出PID+DMC控制效果优于其他两种控制算法，表现出更好的控制精度和较强的鲁棒性。

[1] 张 诤，杨 晶. 大型薄壁复杂铝件铸造技术的现状与发展[J]. 机械管理开发，2005,86(5)：65-68.

[2] 邢小军，刘歌群，闫建国. 基于LabVIEW的分布式调压铸造计算机控制系统设计[J]. 制造业自动化，2004，26(3)：42-44.

[3] 席裕庚. 预测控制[M]. 北京：国防工业出版社，1993.

[4]LianRJ,LinBF,HuangJH.Agreypredictionfuzzycontrollerforconstantcuttingforceinturning[J].InternationJournalofMachineToolandManufacture,2005,45(9): 1047-1066.

[5]ShinskeyFG.Processcontrolsystems—application,designandtuning[M].Beijing:QingHuUniversityPublishingCompany,2002,3.

[6]DavisonEJ，GoldenbergA．Robustcontrolofagenerationservomechanismproblem：theservocompensator[J]．Automatica，1975，11：461-467.