概率统计与圆锥曲线专题测试卷B参考答案

一、选择题

1.A 2.A 3.B 4.D 5.D 6.B 7.A 8.B 9.C 1 0.C 1 1.B 1 2.A 1 3.B 1 4.C 1 5.C 1 6.B 1 7.D 1 8.C 1 9.C 2 0.A 2 1.D 2 2.C 2 3.A 2 4.A

二、填空题

三、解答题

设点A(x1,y1),B(x2,y2),由韦达定理得

所以△A B F1的面积

3 9.(1)因为变量x,y具有线性负相关关系,所以甲是错误的。

(2)由计算可得“理想数据”有3个,即(4,9 0),(6,8 3),(8,7 5),故ξ=0,1,2,3。

所以ξ的分布列为表1。

表1

(2)因为直线过点E(-1,0),所以可设直线的方程为x=m y-1或y=0(舍)。

设A(x1,y1),B(x2,y2),其中y1＞y2。

4 1.(1)由双曲线的定义可知,曲线E是以F1(-,0),F2(,0)为焦点的双曲线的右支,且c=,a=1,易知b=1。

故曲线E的方程为x2-y2=1(x＞0)。

设A(x1,y1),B(x2,y2),由题意建立方程组消去y,得(1-k2)x2+2k x-2=0。

4 2.(1)已知双曲线C的焦点为F1(-2,0),F2(2,0),由双曲线定义||A F1|-|A F2||=2a,得,所以,所以b2=2。

(2)设A(x1,y1),B(x2,y2),因为A,B在双曲线上,所以两方程相减得(x1-x2)(x1+x2)-(y1-y2)(y1+y2)=0,所以,所以

经检验x-2y+3=0为所求直线方程。

所以ξ的分布列为表2。

表2

(2)用C表示事件“甲得2分乙得1分”,用D表示事件“甲得3分乙得0分”,所以

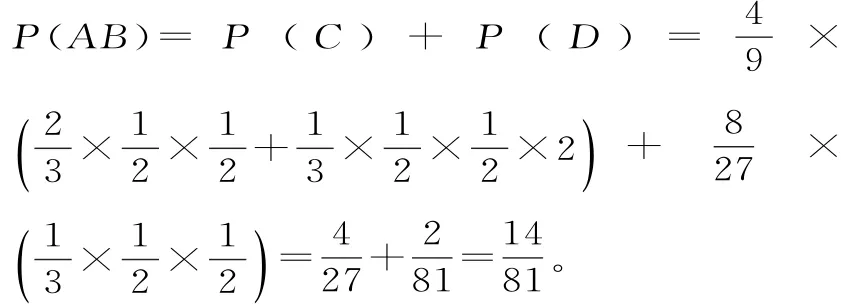
4 4.(1)因为F(0,2),p=4,所以抛物线方程为x2=8y,与直线y=2x+2联立,消去y得x2-1 6x-1 6=0。设A(x1,y1),B(x2,y2),因为x1+x2=1 6,x1x2=-1 6,所以|A F|·|B F|=(y1+2)(y2+2)=(2x1+4)·(2x2+4)=8 0。

(2)假设存在,由抛物线x2=2p y与直线y=2x+2联立,消去y得x2-4p x-4p=0。

设A(x1,y1),B(x2,y2),则x1+x2=4p,x1x2=-4p,可得Q(2p,2p)。

将x1x2=-4p,x1+x2=4p代入得4p2+3p-1=0,解得或p=-1(舍)。

4 5.(1)由抛物线x2=-4y的焦点是椭圆E的一个焦点得c=,所以5=a2-b2。

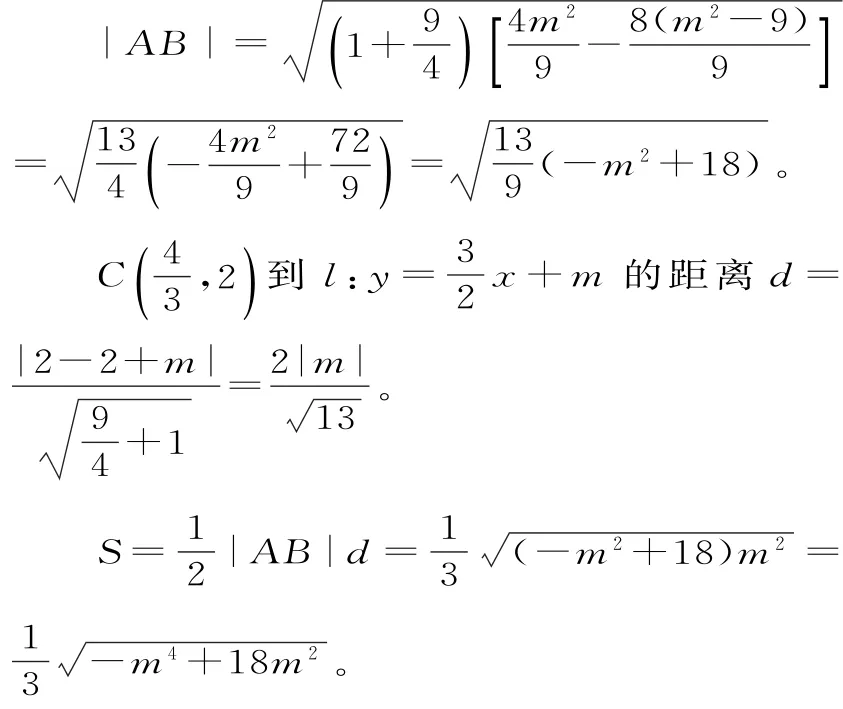
当m2=9,即m=±3时,S最大,对应的直线l的方程为

4 6.(1)由(1-0.2)(1-q)2=0.2 8 8,得q=0.4。

故E(ξ)=0.3 8 4×1+0.2×2+0.0 9 6×3+0.0 3 2×4=1.2。

(2)因为3次射击得分高于2分就是3次射击至少有2次击中目标,所以所求概率为C12×0.8×0.22+0.23=0.1 0 4。