圆锥曲线经典问题透析

■山东省寿光现代中学 陈传璐

高考中圆锥曲线经典问题主要是围绕“圆锥曲线的离心率、焦点弦长公式的应用、轨迹方程的探究、直线与圆锥曲线的位置关系、定值、定点、最值、范围及探索性”等展开的,本文透析如下。

透析1——探究a,c满足的关系求离心率的值或范围

例1 (2 0 1 7年新课标Ⅱ卷原创押题预测卷0 1)如图1,双曲线的中心在坐标原点,焦点在x轴上,A1,A2为双曲线实轴的顶点,B1,B2为双曲线虚轴的端点,F2为右焦点,延长B1A2与F2B2交于点P,若∠B1P B2为锐角,则该双曲线的离心率的取值范围是( )。

图1

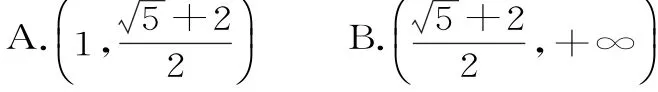
解析:利用向量的夹角为锐角构建a,c的二次不等式,再求解范围。设B1(0,-b),B2(0,b),F2(c,0),A2(a,0),所以因为∠B1P B2为锐角,所以的夹角为锐角,所以,即a2-c2+a c＞0。两边同时除以a2并化简得e2-e-1＜

感悟:椭圆和双曲线的离心率的求值及范围,关键就是确立一个关于a,b,c的方程或不等式,再根据a,b,c的关系消掉b得到a,c的关系式,进而构建关于a,c的齐次式方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围和题设的关系等。

透析2——抛物线焦点弦长有关结论的探究及应用

例2 (2 0 1 7年第二次全国大联考新课标Ⅰ卷)已知抛物线y2=2p x(p＞0)的焦点为F,抛物线上一点P的横坐标为2,Q(x,y),P(x0,y0)。过F且倾斜角为3 0°的直线交抛物线于A,B两点,O为坐标原点,则△O A B的面积为____。

解析2:用方程可探究抛物线焦点弦长的有关结论,注意简化运算途径的选择。

感悟:本题解析2的探究过程可得到抛物线焦点弦的几个常用结论:

(1)弦端点A(x1,y1),B(x2,y2)的坐标之间的关系为

(3)弦被焦点分弦所成的两焦半径的倒数和为p的倒数的2倍,即

透析3——定点和定值问题的探究

上,椭圆C的左焦点为(-1,0)。

(1)求椭圆C的方程。

(2)如图2,直线l过点T(m,0)(m＞0)交椭圆C于M,N两点,A B是椭圆C经过原点O的弦,且MN∥A B,问:是否存在正数m,使得为定值?若存在,请求出m的值;若不存在,请说明理由。

图2

解析:(1)由左焦点(-1,0)可得c=1,因为b2=a2-c2,所以b2=a2-1。

(2)假设正数m存在,设直线l:y=k(x-m),M(x1,y1),N(x2,y2),联立方程消去y整理得(3+4k2)x2

设A(x3,y3),B(x4,y4),联立方程组消去y整理得

透析4——圆锥曲线中的最值或范围问题

例4 (2 0 1 7年新课标Ⅰ卷原创押题预测卷0 1)已知椭圆的左右焦点分别为F1,F2,上下顶点分别是B1,B2,C是B1F2的中点,若且C F1⊥B1F2。

(1)求椭圆C的标准方程;

(2)过F2的直线l与椭圆C交于不同的两点A,D,求△F1A D的面积的最大值。

解析:(1)由题意可得F1(-c,0),F2(c,,所以

由C F1⊥B1F2,可得,即

(2)设 A(x1,y1),D(x2,y2),S△F1AD=。由题意知,直线l的斜率不为零,可设直线l的方程消去x整理得为x=m y+1,由(3m2+4)y2+6m y-9=0,所以y1+

因为直线l与椭圆C交于不同的两点,所以Δ＞0,即(6m)2+3 6(3m2+4)＞0,m∈R, 故 S△F1AD=|y1-y2|=。令t=,则t≥1,则。令,由函数的性质可知,函数f(t)在上是单调递增函数,即当t≥1时,f(t)在[1,+∞)上单调递增,因此有f(t)≥f(1)=,所以S△F1AD≤3,所以当t=1,即m=0时,S△F1AD最大,最大值为3。

感悟:解决圆锥曲线中的最值或范围问题有两种途径:一是用圆锥曲线的定义和平面几何的有关结论来解决;二是将圆锥曲线中的最值或范围问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法及均值不等式法求解,其中换元法在化繁为简时需认清函数的特征。