直线与圆锥曲线的位置关系的常见类型及解题策略

■河南省温县第一高级中学 马惠云

高考解析几何解答题第二问大多考查直线与圆锥曲线的位置关系,主要问题是求范围、方程、定值或最值等。其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题在思想上要重视数形结合思想、方程思想、函数思想、化归思想、分类讨论思想的应用。方法上其常规思路是先把直线方程与圆锥曲线方程联立,消元、化简,然后应用根与系数的关系建立方程,从而将几何问题转化为代数问题,基本的运算技巧是设而不求,整体代入。但是也要注意运用平面图形的几何性质发现某些量的值或数量关系,从而达到简化运算的目的。

例1 设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点。若|A F|=3|B F|,则l的方程为( )。

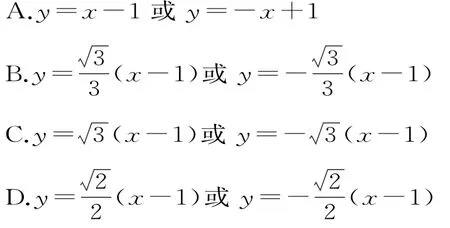
图1

解法一:如图1所示,作出抛物线的准线l1及点A,B到准线的垂线段A A1,B B1,并设直线l交准线于点M。设|B F|=m,由抛物线的定义可知|B B1|=m,|A A1|=|A F|=3m。由B B1∥,所以|MB|=2m,则|MA|=6m。故∠AMA1=3 0°,得∠A F x=∠MA A1=6 0°,结合选项知C项正确。

例2 已知曲线Γ上的点到点F(0,1)的距离比它到直线y=-3的距离小2。

(1)求曲线Γ的方程。

(2)曲线Γ在点P处的切线l与x轴交于点A。直线y=3分别与直线l及y轴交于点M,N。以MN为直径作圆C,过点A作圆C的切线,切点为B,如图2所示。试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段A B的长度是否发生变化?证明你的结论。

图2

解析:(1)解法一:设S(x,y)为曲线Γ上任意一点,依题意,点S到F(0,1)的距离与它到直线y=-1的距离相等,所以曲线Γ是以点F(0,1)为焦点,直线y=-1为准线的抛物线,所以曲线Γ的方程为x2=4y。

(2)当点P在曲线Γ上运动时,线段A B的长度不变。证明如下:

设P(x0,y0)(x0≠0),则

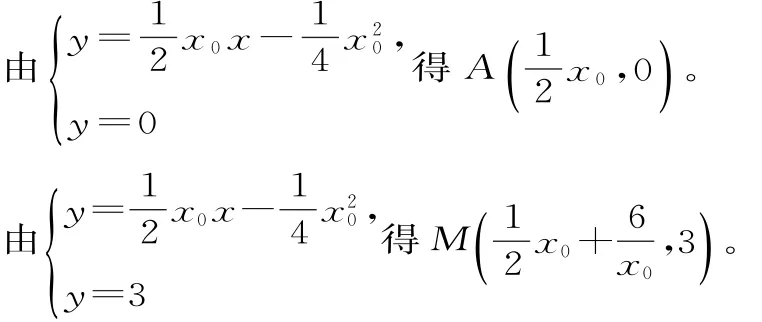
方法小结:(1)求抛物线的标准方程时一般要用待定系数法求p的值,但首先要判断抛物线是否为标准方程,若是标准方程,则要由焦点位置(或开口方向)判断是哪一种标准方程。

(2)注意应用抛物线定义中的距离相等进行转化,从而解决问题。

(3)直线与抛物线有一个交点,并不表明直线与抛物线相切,因为当直线与对称轴平行(或重合)时,直线与抛物线也只有一个交点。